内置交叉工字钢的圆钢管混凝土柱子力学性能研究

万新民

0 引言

本文依托工程为某酒店，该酒店共26 层，其中包含地下1 层以及地上25 层。酒店主体结构共包含三个部分，一部分为地下室，一部分为裙楼，一部分为塔楼，其中地下室用于停车（-1 层），裙楼用于商业接待等（1～5 层），塔楼为酒店住宿房间（6～25 层）。所用结构均为现浇框架-剪力墙结构，由于空间转换较大，因此在部分结构变换位置采用空间斜柱进行高位转换，在上部荷载作用下，该柱承受较大轴力及弯矩，如若设计不当，极易引发安全事故，因此有必要对该现浇混凝土柱进行承载力力学性能分析。

1 分析内容概况

1.1 构件尺寸

根据已有试验结果，模拟的截面尺寸见图 1 及表 1。

图1 构件截面尺寸

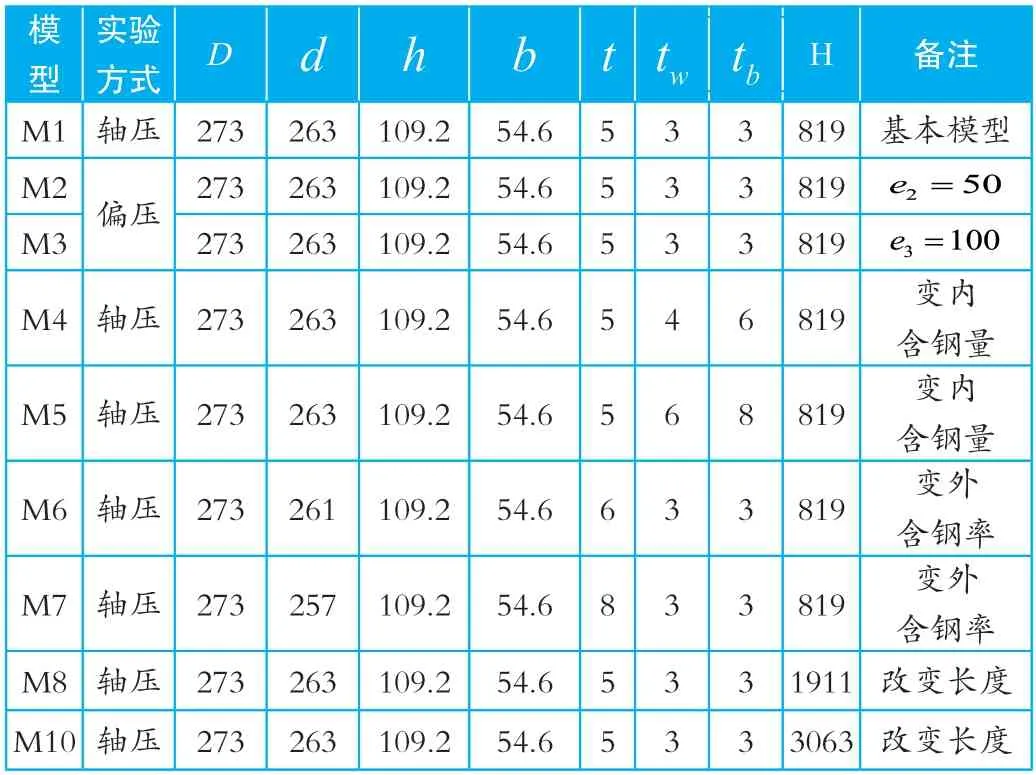
表1 构件有关参数

1.2 材料及特性

本实验M1～M10 的混凝土均选用C60 混凝土，但在混凝土标准试块立方体抗压强度抗压实验中，不同模型的抗压强度略有不同，共分为两种，其一为M1～M8 立方体试块，其抗压强度为标准值60MPa；其二为M9～M10 立方体试块，其抗压强度为标准值70MPa，略大于标准值。钢材使用强度较高的Q235钢材，经强度检验，钢材的极限抗拉强度及屈服强度如表2 所示：

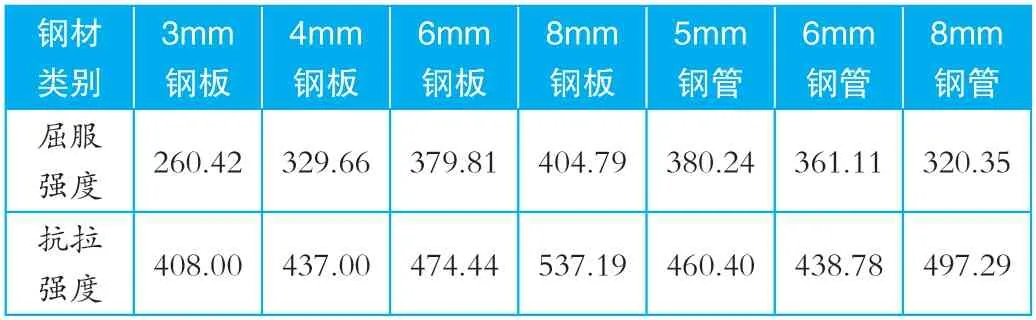
表2 构件参数

2 数值计算

数值计算过程中，所用材料的本构模型选择尤其重要，对于本文研究的钢管混凝土柱而言，由于钢筋为弹性结构，故其本构模型无需选取，按默认材料设置即可。但对于混凝土而言，由于材料的高度非线性及脆性性质，若在素混凝土结构中，则按规范选择即可，但由于本文为钢管混凝土，在钢管的共同作用下，混凝土的力学性能得到较大改善，其延展性交素混凝土有较大提升，承载力也有很大的提高，如若按照规范进行本构选择，则容易造成较大的材料浪费，给工程经济造成极大的损失。因此，本文通过查阅相关文献资料，并采用文献所建议的约束混凝土受压本构模型进行数值分析计算，具体计算公式如下：

2.1 混凝土的本构关系

2.2 钢材的本构关系

除混凝土外，钢管混凝土的另外一种材料也至关重要，那就是钢材，在数值模型中，钢材的受力关系一般分为四个阶段，因此，其本构宜选用四折线模型，分别对应钢材前期受力时弹性阶段的线弹性本构以及屈服阶段、强化阶段和颈缩阶段对应的非线性本构，各阶段本构关系如下公式（2）所示。

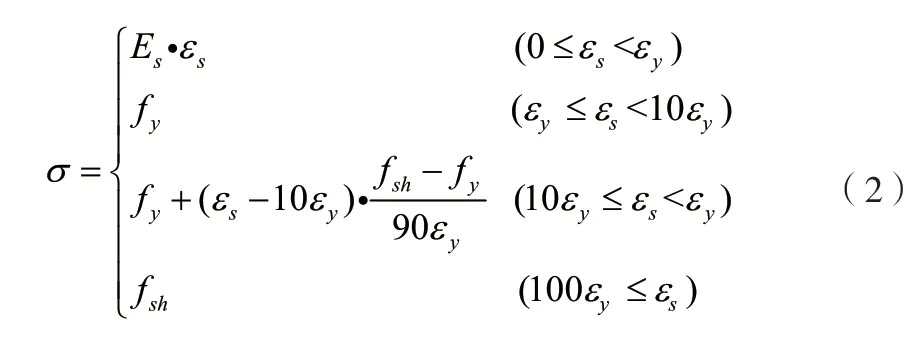
3 相关参数的设置

在Abaqus 混凝土参数设置模块中，定义了三种本构模型，一种为弥散开裂模型，适用于隐式算法计算；第二种为脆性断裂模型，适用于一般的脆性断裂模型计算；第三种为损伤塑性模型，该模型综合了前两种模型优点，能同时适用于上述两种环境，因此本文混凝土本构选择第三种。模型参数如表3 设置。

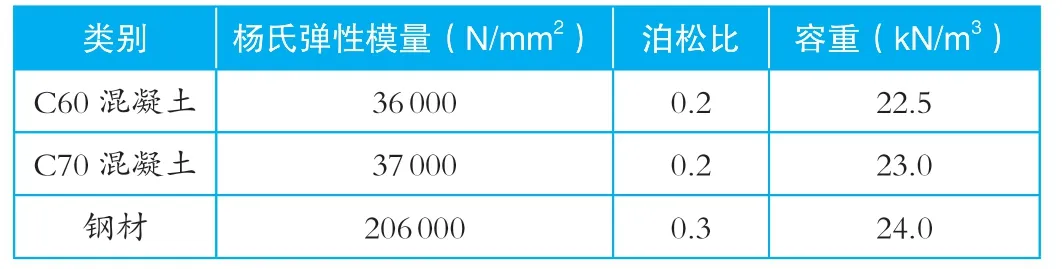
表3 数值模型计算参数

在损伤塑性模型中，当混凝土受压时，其膨胀角会随着增大，但刚度却不会改变，因此对于此模型，在一定程度上混凝土的承载力会随着压力的增大而增大。本文中膨胀角取30，偏心0.1，双向受压时乘以系数1.16。此外粘性系数也会影响混凝土结构的承载力变化，也是数值模型计算中的一个重要参数，其大小对模型运行收敛速度以及荷载——位移曲线影响较大，因此其取值也尤其重要，当系数过大时，容易导致模型结构刚度过高，无法反映真实情况，取值较小时，模型刚度较小，难以收敛。本文按默认值设置，取值为0。

4 接触的定义

在Abaqus 数值分析软件中的接触定义中，涉及因素众多。在钢管混凝土构件中，包括对上下盖板、外置钢管、内置型钢以及灌注混凝土各部件的相互作用。在本模型中，套管与混凝土法向使用“硬”接触定义，切向则采用库伦摩擦方式定义；由于型钢浇筑在核心混凝土中，因此在接触定义时，使用embedded 方式定义；套管与上下盖板则是通过shell to solid 方式进行定义；内置型钢与盖板之间，则需要考虑内置型钢的受压形式，当内置型钢处在轴压范围内，则采用shell to solid 方式进行定义；当内置型钢处在偏压范围时，则将shell to solid 接触定义模块去除，从而保证模型能够真实模拟偏压效果。此外当偏压较大时，柱长越长，重力二阶效应也就越明显，故还需对柱子长度进行考虑。

5 边界条件

在数值模型分析中，模型边界条件的选择尤其重要。模型边界条件设置时，模型的边界条件应与实际情况相对应。对于轴压柱的边界荷载，一般沿用位移加载方式，通过在柱子的一端设置为固定连接，即1=2=3=1=2=3=0；另一端开放施加荷载，初始边界如固定端设置，后一步设为1=2=1=2=3=0，3=20mm；对于偏压柱的边界荷载，考虑实际实验中滚轴与球绞间的转动能力较差，因此在数值模型的边界设置中，需将其考虑进去，故边界设置分为两步：第一步沿用上述轴压边界条件，当模型位移下压2mm之后，再进行第二步，将柱子下端铰接处理，使其获得足够的转动能力，即将1=2=3 设置为0，同时上端设置为1=2=1=2=3=0，3=-7mm。

6 求解控制

在Abaqus 的求解控制中，荷载通过荷载步施加。在每一个特定的荷载增量步的求解过程中，Abaqus 都需要对该增量步进行数次迭代，并在这若干迭代步中寻求一个最终解用以输出，所有增量步在迭代求解过程中的响应总和便是对于模型最优解的非线性的近似解。

在本模型中，当模型中柱长较短时，可以直接调用Abaqus/Standard 模块中的一般静力求解器进行求解，但当模型柱长超过一定值时，柱子被视为长柱或中长柱时，其破坏特征较短柱有所改变，使用静力求解器无法满足实际情况需要，其破坏形式变为屈曲破坏，因此需改变分析方式，采用Buckling 对其进行屈曲分析，主要操作步骤为：在Buckling 中输出节点位移，通过修改keyword，增加语句

*node file

u，

再拷贝相同的模型，将buckling 替换成riks 求解步，通过引入输出的节点文件，inp 语句为

*imperfection file=buckling1，step=1（引入工作名为buckling1，对应的荷载步为1 的文件）

1,1e-2（第一模态的0.01）

2,1e-3（第二模态的0.001）

在本文中，由于长短柱差异较大，分析时短柱考虑一般静力求解器进行分析，长柱按上述要求考虑使用弧长法对其进行非线性屈曲分析。如此，不仅能够区别短柱和长柱，在长柱分析时，还能够考虑变形过程中的负刚度问题，输出长柱变形过程中的弧长-位移曲线，再通过monitor 中加载的增量比例及加载的荷载，二者相乘得到对应弧长的荷载，从而求解出模型荷载-位移曲线。

7 有限元结果

通过有限元计算，得到各模型的变形图，限于篇幅现只列出M3、M5、M10 试件结果，有限元结果如图2～4 所示，相应应力应变荷载位移曲线如图5～7 所示。

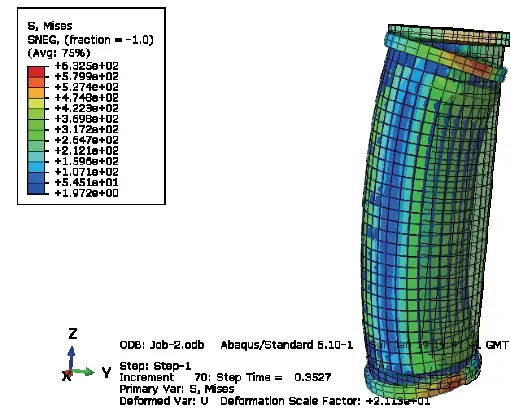
图2 M3 偏压短柱应力变形图

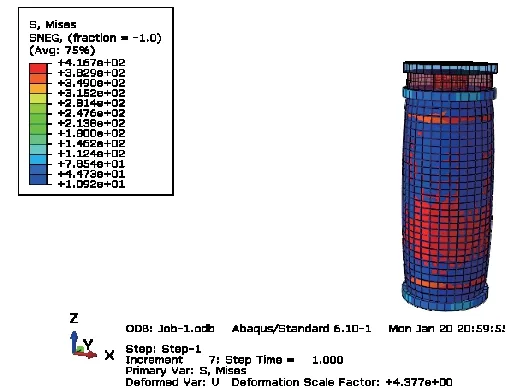
图3 M5 轴压短柱应力变形图

图4 M10 轴压长柱应力变形图

综上图2～4 可以发现，无论何种状态下，各试件在极限应力状态时均会出现不同程度的变形，对于图2 中的偏压短柱而言，出现明显的弯曲变形；对于轴压短柱而言，则出现明显的压缩变形；对于轴压长柱而言，因柱长过大，则既表现出明显的压缩变形又出现明显的弯曲变形。

8 有限元结果与实验结果的对比

根据有限元计算结果，可以看出计算结果与试验结果基本一致，如图5～7 所示。

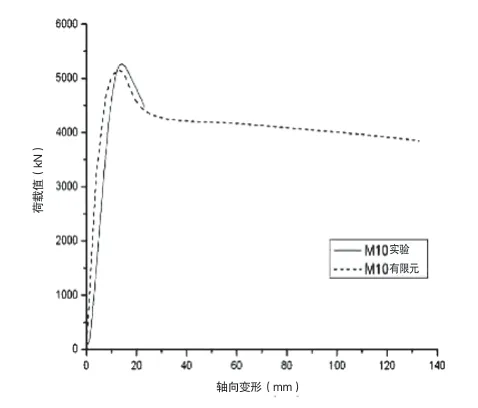
图5 M5 轴压短柱荷载位移曲线

图6 M3 轴压短柱荷载位移曲线

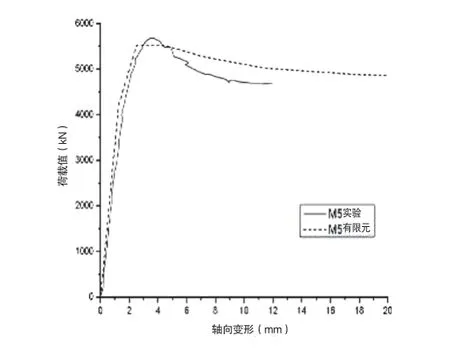
图7 M10 轴压短柱荷载位移曲线

通过上述ABAQUS 数值分析曲线可知，有限元计算结果较为理想，曲线所表现出的趋势与理论计算及实验曲线基本一致，有明显的弹塑性变形，从弹性段上升到极限承载力后下降。此外，从分析结果可以看出，对于轴压短柱及偏压短柱而言，由于柱长相对较短，其弹塑性变形曲线下降阶段较缓，表明柱子过渡阶段较长，延性较好；但在轴压长柱中，由于柱长相对较长，变形过程中变形曲线下降明显，说明延性较差。由此可知，在钢管混凝土柱中，一定体积条件下，随着柱长的提高，其延性反而会降低，承载性能也会随之下降。经有限元分析计算，对于轴压短柱M5，其极限承载力N为5 528.0 kN，实验结果为N为5 680kN，N/ N为0.9732；对于偏压短柱M3，有限元计算的极限承载力N为2 078.0 kN，实验结果为N为2 001.0 kN，N/ N为1.0385；对于轴压长柱M10，有限元计算的极限承载力N为5 146.0 kN，实验结果为N为5 265.0 kN，N/ N为0.9774。所以模拟结果与试验结果相差不大。综上所述，Abaqus 有限元分析能够较好地模拟内置交叉工字型钢的圆钢管混凝土柱子的轴压偏压及长短柱实验。

9 结论

本文基于ABAQUS 数值分析软件，研究了不同情况下钢管混凝土柱的轴压、偏压情况，进而探讨其相应的力学性能。经对比分析发现，数值分析结果与模型实验结果基本一致，并得出轴压长柱由于柱长相对较长，变形过程中变形曲线下降明显，延性较差验，短柱弹塑性变形曲线下降较缓，表明柱子过渡阶段较长，延性较好的结论，证实了采用有限元计算在混凝土柱子力学性能研究中应用的可靠性。