下部结构对拱形波纹钢屋盖结构承载力影响分析

申成军

0 引言

拱形波纹钢屋盖结构从20 世纪90 年代初在我国应用以来已有近30 年时间了，虽然轻型门式刚架结构的兴起应用量有所下降，但是由于这种结构形式具有防水效果好、施工速度快、内部空间大等优点，依旧有大量的厂房、仓库、餐厅、体育场馆等工程采用了这种结构形式。但是这种结构形式计算分析的方法比较复杂，通常由专业厂商进行上部结构拱形波纹钢屋盖的分析计算，下部结构由设计院分析计算，这种两阶段的设计方法忽略了下部结构对拱形波纹钢屋盖结构承载力的影响，有时存在一定的安全隐患。

拱形波纹钢屋盖结构有多种板型，本文以YT6118 型为例探讨下部结构刚度变化对钢屋盖承载力的影响，其截面形状如图1 所示。

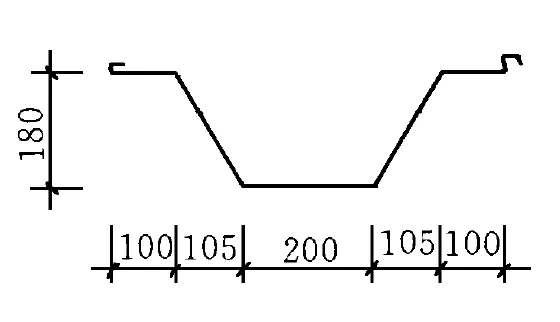
图1 YT6118

本文以有限元软件STAAD 建模，以板单元模拟钢屋盖受力，首先验证了用STAAD 软件分析金属波纹钢屋盖结构的可行性，然后研究了下部结构横向和纵向刚度变化对屋盖承载力的影响，最后总结了研究结论并提出了设计建议。

1 软件有效性验证

文献[2]中对拱形波纹钢屋盖进行了足尺模型实验，现在选取22m 跨度的钢屋盖进行对比分析，在文献[1]的实验中，钢屋盖的拱脚用自攻螺钉固定在异形角钢上，异性角钢固定在地面上的混凝土梁上。实验钢屋盖的矢跨比为0.2，板厚为1mm，钢板采用上海宝钢生产的TstE28 彩色镀锌钢板，材料的弹性模量为2.06×105Mpa，屈服强度为280 Mpa，抗拉强度为370 Mpa，实验的半跨极限承载力为667.81Pa，下面用STAAD 软件进行验证，按实验的跨度和拱高进行建模，拱脚采用固定铰支座，实验时侧向加了脚手架进行约束，模型加了侧向约束，如图2 所示。

图2 计算模型

对模型施加 667.81Pa 的荷载后，考虑P-Δ 效应的计算分析，分析完成后Von-Mises 应力在实验的极限荷载作用下达到了460N/mm，超过了材料的抗拉强度，证明软件的计算结果与实验结果是基本吻合的。最大应力处为非加载半跨的沿跨度方向约1/8 的位置。此外，软件输出的最大竖向位移为320mm，挠跨比为1/69。

经过以上的计算分析，表明用STAAD 分析拱形波纹钢屋盖结构是可行的。必须说明的是，软件没有考虑结构的初始缺陷以及横向波纹对钢屋盖整体承载力的不利影响，也没有考虑纵向肋纹和锁边对整体承载力的有利影响。

2 下部结构横向刚度对钢屋盖承载力的影响分析

为分析下部结构横向刚度对钢屋盖承载力的影响，分别取12m 跨、22m 跨的钢屋盖为计算样本，屋盖的矢跨比均取0.2，材料材质均取TstE28 型彩色镀锌钢板，模型纵向均取21 条板共12.81m，设2 个开间，柱距6.1m，在钢屋盖下建立钢梁和钢柱，钢梁和钢柱根据跨度不同选择不同的截面规格，以模拟真实工程中屋盖的结构布置，建立的三维模型如图3 所示。

图3 三维模型

先分析12m 跨度的钢屋面，钢屋面的钢板厚度为0.8mm，半跨加载500Pa，纵向钢梁采用矩形钢管250mm×200mm×6mm×6mm，钢柱采用方钢管250mm×250mm×6mm×6mm，钢柱高度从3m 开始逐渐增加，直到计算出的应力超过300N/mm。得到的钢屋盖最大应力与柱高关系见图4 所示，最大竖向位移与柱高关系见图5 所示，屋盖挠跨比（挠度与跨度的比值）与柱高的关系见图6 所示，柱子侧移比（柱顶侧移值与柱高的比值）与柱子高度的关系见图7 所示。

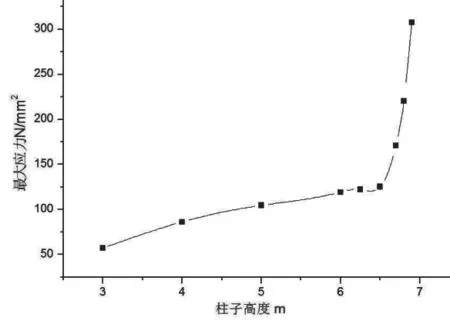
图4 12m 跨钢屋面最大应力与柱高关系图

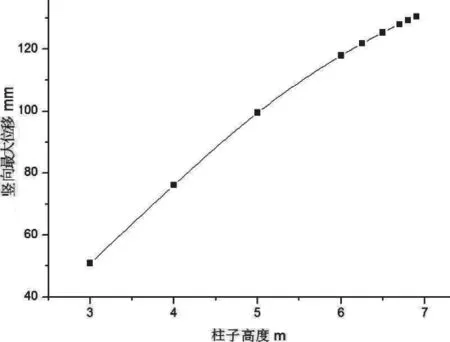
图5 12m 跨钢屋面最大竖向位移与柱高关系图

图6 12m 跨钢屋面挠跨比与柱高关系图

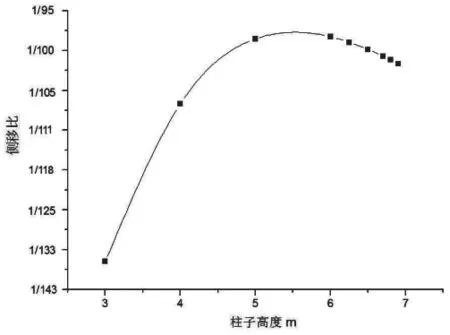
图7 12m 跨钢屋面侧移比与柱高关系图

对于12m 跨度的钢屋面，随着柱高的增加，钢屋盖的应力水平先是缓慢增加，当柱高增加到一定高度，钢屋盖的应力变化开始迅速增加，意味着屋盖进入破坏，屋盖的最大竖向位移随着柱子高度的增加逐渐增大，挠跨比随着柱子高度的增加逐渐增大，侧移比一开始随着柱子高度的增加逐渐增加，后来由于侧移值增加的幅度没有柱子高度大，侧移比呈下降趋势。

22m 跨度的钢屋面的钢板厚度为1.0mm，半跨加载500Pa，纵向钢梁采用矩形钢管300mm×250mm×8mm×8mm，钢柱采用方钢管300mm×300mm×8mm×8mm，钢柱高度从3m开始逐渐增加，直到计算出的应力超过300N/mm。得到的钢屋盖最大应力与柱高关系见图8 所示，最大竖向位移与柱高关系见图9 所示，屋盖挠跨比与柱高的关系见图10 所示，柱子侧移比与柱子高度的关系见图11 所示。

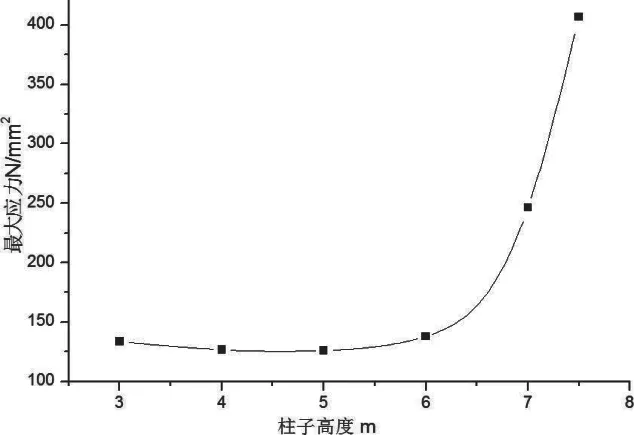
图8 22m 跨钢屋盖最大应力与柱高关系图

图9 22m 跨钢屋盖最大竖向位移与柱高关系图

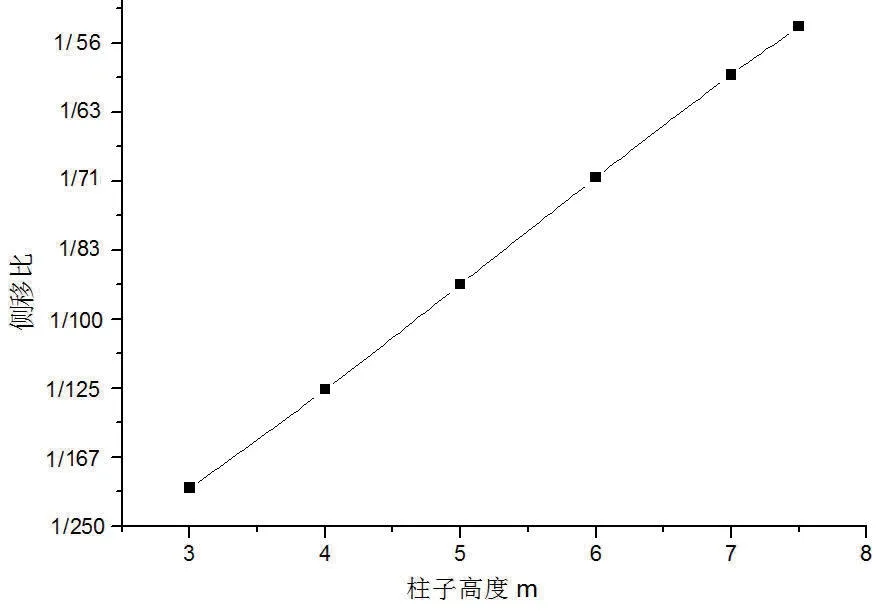
图10 22m 跨钢屋盖挠跨比与柱高关系图

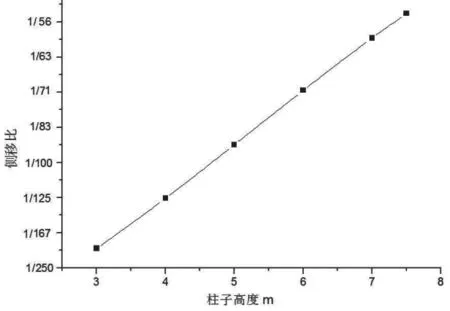
图11 22m 跨钢屋盖侧移比与柱高关系图

对于22m 跨度的钢屋盖，发现随着柱高的增加，钢屋盖的应力水平一开始略有下降然后缓慢增加，应力略有下降是因约束放松造成的，当柱高增加到一定高度，钢屋盖的应力变化开始迅速增加，意味着屋盖进入破坏，屋盖的最大竖向位移随着柱子高度的增加逐渐增大，挠跨比随着柱子高度的增加逐渐增大，侧移比随着柱子高度的增加逐渐增加。

3 下部结构纵向刚度对屋盖承载力的影响分析

钢屋盖的纵向长度决定了下部结构的纵向长度，下面通过调整钢屋盖的纵向长度带来的下部结构纵向刚度的变化来分析钢屋盖承载力的变化。

研究方案为分别取12m、22m 跨度的钢屋盖计算模型，在纵向不断增加单元板（每3 条板为一组单元板）的数量，直至单元板数量的增加对屋盖承载力的影响不明显。然后试图找出屋盖纵向长度变化与钢屋盖承载力的关系。

计算模型的矢跨比取0.2，均施加半跨均布荷载667.81Pa，拱脚均为固定铰支座；12m 跨钢屋面的钢板厚度取0.8mm，22m 跨钢屋面的钢板厚度取1.0mm，材料均取TstE28 型彩色镀锌钢板。

经计算分析12m 跨度的计算模型长跨比（纵向长度与跨度的比值）与最大应力的关系如图12 所示，长跨比与最大竖向位移的关系如图13 所示。

图12 12m 跨钢屋面最大应力与长跨比关系图

图13 12m 跨钢屋面最大竖向位移与长跨比关系图

经计算分析22m 跨度的计算模型长跨比与最大应力的关系如图14 所示，长跨比与最大竖向位移的关系如图15 所示。

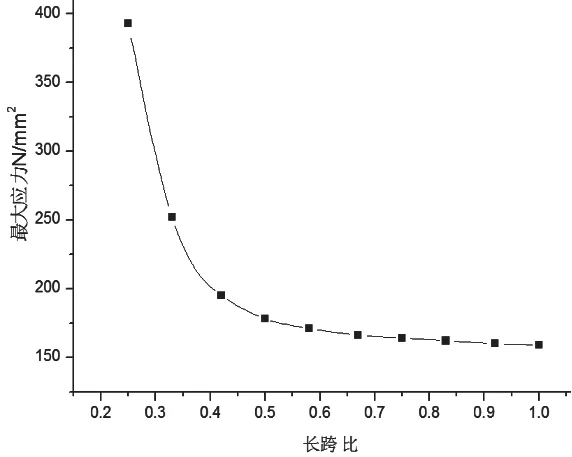
图14 22m 跨钢屋盖最大应力与长跨比关系图

图15 22m 跨钢屋盖最大竖向位移与长跨比关系图

经过以上的分析可以发现，随着钢屋盖纵向长度的增大，钢屋盖纵向长度对应力和位移的影响逐渐减弱，一般当长度达到8 组单元板的长度时，对应力和位移的影响就已较小。若用长跨比来描述，总体而言，当拱形钢屋盖的长跨比达到0.8 时，纵向刚度对屋盖承载力的影响基本保持稳定，跨度小的比跨度大的更易保持稳定。

在实际工程应用中，很少有屋盖长度小于跨度的情况，也就是说一般情况下可以忽略下部结构长度变化对屋盖承载力的影响。在特殊情况下，当钢屋盖的用量很少，少于8 组单元板时，应该考虑屋盖纵向刚度较小对屋盖整体承载力的影响。

4 结语

经过以上的分析可以得出以下结论：

当下部结构的横向刚度较差时不可忽略下部结构横向刚度的影响，这时在分析拱形波纹钢屋盖的承载力时，应与下部结构整体建模进行分析。

下部结构纵向刚度对上部结构的承载力有不同程度的影响，当屋盖的纵向长度小于8 组单元板的宽度时，不可忽略下部结构纵向刚度的影响，这时在分析拱形波纹钢屋盖的承载力时，应与下部结构整体建模进行分析。

此外，建议在设计这种结构时屋盖的挠跨比宜控制在1/150 以内，若墙体采用轻质墙面，下部结构的侧移比宜控制在1/150 以内，在有可靠的分析时，可放宽到1/100。另外，有限元分析表明，最边处的条板往往应力较大或变形过大，这种结构应进行山墙封闭处理，若为山墙开敞结构，边部条板应采用钢桁架在底部加强。