基于SEM-MC的地铁车站深基坑施工危险性测度研究*

王永祥，廖 婷，李洪高，詹同江，耿大新

(华东交通大学 土木建筑学院，江西 南昌 330013)

0 引言

地铁车站深基坑是典型的“危大工程”，具有构筑物深埋、周边环境复杂、施工难度高、风险致损大等特点，其施工过程主要包括基坑支护、降水排水、土方开挖、结构施工等。在与复杂的周边环境耦合作用下，潜藏许多风险因素，若未能识别与评测其蕴含的风险性，一旦发生事故，后果极其严重。因此，在地铁车站建设前，需采取科学有效的方法对地铁车站深基坑开展危险性评测研究。评测结果既可以让承包商识别面临的风险程度，采取预防性的应对措施，也可以让业主、监理单位、政府主管部门开展有效风险管控。

影响地铁车站深基坑施工安全的因素较多且各影响因素之间互相影响，具有密切的关联性。目前，国内外学者对如何科学评测地铁车站深基坑施工危险性进行了大量的研究。陈波等[1]通过层次分析法(AHP)构建多因素深基坑施工危险性测度模型；周红波等[2]采用故障树-AHP模型对地铁隧道竖井基坑围护结构失稳进行风险评价。上述研究都是常规确定性施工危险性测度方法，不足之处是未考虑到施工危险性测度中的不确定性。Konstantinos等[3]利用模糊层次分析法，对雅典地铁车站施工危险性进行测度研究；Zhang等[4]建立模糊贝叶斯网络—模糊层次分析模型，根据对基坑塌方事故的统计分析，对深基坑施工安全风险进行测度研究。这些研究引入了模糊理论对施工危险性进行不确定性分析。除引入模糊理论外，宋博[5]利用数据包络法-反向传播神经网络模型对指标的非线性关系进行分析，并动态预测地铁深基坑施工危险性等级；潘梦真等[6]等运用改进的相互作用矩阵对基坑安全施工风险进行评价。

综上所述，之前的学者虽然改进了传统施工危险性测度方法，但多数仅考虑各影响因素对深基坑施工风险的单独作用，鲜少考虑多因素之间的耦合效应，同时，对深基坑施工危险性测度研究的方法主观性较强，缺乏客观评测手段。因此，针对现有研究的不足，本文拟联合运用结构方程模型(SEM)与蒙特卡洛(MC)方法，采用SEM计算指标权重，结合MC方法，减少数据来源主观性，对地铁车站深基坑施工危险性进行测度研究，并将其运用到具体案例中验证该方法的科学性与有效性，从而为地铁车站深基坑施工危险性测度研究提供一定的支撑和参考。

1 研究方法

1.1 危险性测度指标体系构建

地铁车站施工一旦发生事故，往往会导致人员伤亡、工期延误、经济损失等严重后果。对地铁车站深基坑风险管理应严格遵循《安全生产法》中的“安全第一、预防为主”的方针。预防的前提是准确识别各种风险并科学地予以评测，而传统风险识别方法大多只考虑单一风险因素或多风险因素的简单叠加，往往不能适应地铁车站深基坑工艺的复杂性和关联性。单一风险因素往往不易直接引发风险事故，而是与其他风险因素耦合导致风险事件发生。为此，基于风险耦合理论，从深基坑施工安全风险耦合机理进行初步分析，基坑开挖、基坑支护、降水排水和周边环境4个维度出发，如图1所示。

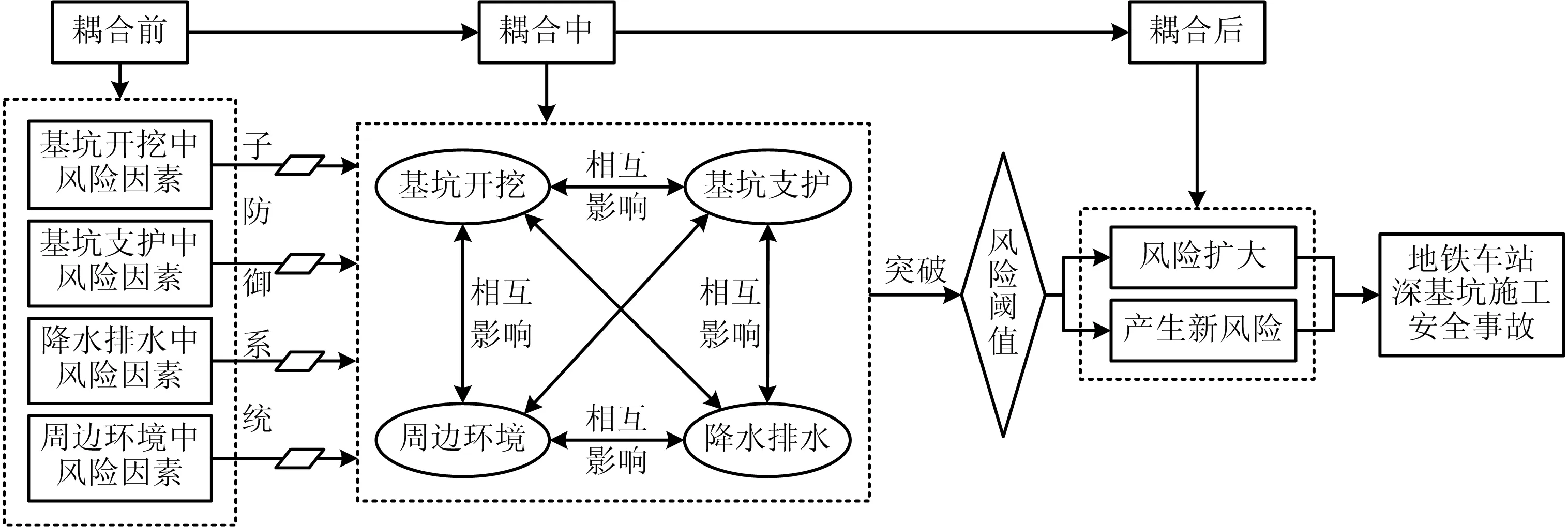
图1 地铁车站深基坑施工风险耦合机理

由图1可知，地铁车站深基坑施工作为1个复杂的系统工程，其内部因素之间交互耦合会增加风险事故发生的概率，如地铁车站深基坑周边环境会影响土方开挖技术参数设置，同时也会影响降水排水方案布置。相反，不合理的降水排水方案会导致基坑积水严重，使基坑内土体力学性能变差，抗拉锚杆锚固力降低，土体侧应力增大，周边水土流失严重，极易产生基坑支护失稳以及周边建筑物不均匀沉降等消极后果。因此，需要考虑风险耦合作用。

参考《地下铁道工程施工质量验收标准》(GB/T 50299—2018)[7]，考虑风险之间的耦合作用，从基坑支护、基坑开挖、降水排水以及周边环境4个维度建立危险性测度1级指标，再参考既有研究[8-11]和相关标准规范[12-14]建立2级指标群，组织相关专家进行会审，选取抗拉锚杆、支护形式、支撑节点刚度等16种地铁车站深基坑施工危险性测度指标以及人员伤亡、经济损失和工期损失3种事故后果构建深基坑施工危险性测度指标体系，如图2所示。

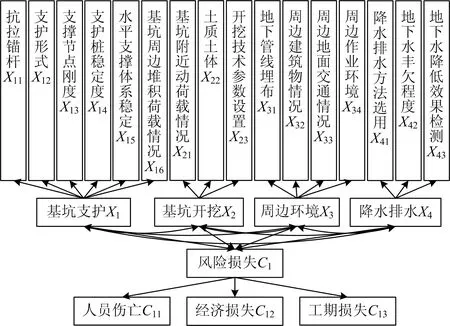
图2 地铁车站深基坑施工危险性测度指标体系

1.2 SEM-MC危险性测度模型

1)基本模型构建

结构方程是1种将因素分析和路径分析相结合的统计方法[15]。该方法引入潜变量概念，测量变量通过因素分析反映潜变量，再利用路径分析找出潜变量之间的关系。

蒙特卡洛方法，是以数理统计理论为基础，利用软件产生大量随机数并进行多次模拟得到客观目标概率分布及概率特征值的1种随机模拟方法。其通常被用于对项目的不确定性分析和风险分析，能够更客观更准确反映不确定性因素的影响。

参考《城市轨道交通地下工程建设风险管理规范》(GB 50652—2011)[16]，危险度一般由风险可能发生概率与风险损失值简单相乘所得，但并不能客观反映风险水平。因此，在综合考虑主观性与多因素耦合的基础上，联合运用SEM与MC方法，建立地铁车站深基坑危险性测度模型，如图3所示。考虑风险耦合作用，构建结构方程模型，利用SEM能够处理复杂多变量数据的特性，求出各影响因素权重并识别主要影响因素，同时根据各因素数据特征，利用MC模拟产生一系列符合要求的数据，求出潜变量的概率分布，最后结合风险损失值与风险因素权重求出危险度R，如式(1)所示：

“熟读唐诗三百首，不会吟诗也会吟。”在强化背诵积累的过程中，力求做到家校结合，共同做好学生阅读、积累、背诵的管理和引导教育工作。近年来，越来越多的学校和家庭更加重视古诗文的学习和背诵，越来越多的孩子成为传统文化的受益者。每日坚持阅读，每周坚持背诵古诗文，不但开阔了学生的视野，增强了传统文化的学习和感悟，而且锻炼了学生的积累程度和记忆力。

图3 SEM-MC危险性测度模型

(1)

式中：wi为潜变量权重值；Pi为潜变量可能性分值；wj为风险损失权重值；Clj为风险损失值。

2)风险等级划分

依据《城市轨道交通地下工程建设风险管理规范》[16]，将风险发生概率、风险损失程度划分为5个等级，1～5级表示风险发生的概率与损失程度逐级递增，将危险度划分为4个等级，1～4级表示危险度也逐级递增。其计算如式(2)所示：

Rs=Ps×Cs

(2)

式中：Rs为危险度；Ps为风险发生概率；Cs为风险损失程度。

依据文献[16]，对危险度的评判标准如表1所示。

表1 危险度等级表

2 算例分析

2.1 工程概况

选取南昌地铁双港站为研究对象。双港站为地下2层岛式车站，站台宽11 m，车站主体长约321 m，站台中心处结构高度为13.10 m，覆土厚约2.95 m。该站横穿双港大道，大致呈南北走向，西侧有高层居民楼，下穿江西省日报社仓库，管道分布较少，地下水主要为孔隙性潜水与裂隙性潜水，在勘查期间水位埋深0.5～6.2 m。车站采用明挖顺作法施工，围护结构采用钻孔灌注桩加内支撑支护体系。南端头井基坑深度约为16.194 m，北端头井基坑深度约为18.34 m，站台中心里程处基坑深度约14.75 m，在基坑开挖深度范围内岩性主要为中风化千枚岩，开挖时易于挖进，但易坍塌，其力学性能较差，因此施工难度较大。

2.2 地铁车站深基坑施工危险性测度结构方程模型的构建

1)量表设计

采用调查问卷法，对该站深基坑施工危险性测度2级指标进行数据收集，问卷分3部分，第1部分为问卷指导语，第2部分为调查对象的个人背景，包括：教育背景、工作单位、工作年限3个基本项，第3部分为问卷问题。问卷调查采用Likert scale，根据深基坑施工危险性测度指标体系将问题分为5组设置19道题，利用1，2，3，4，5分别代表可忽略影响、较小影响、中等影响、较大影响、严重影响。部分题项如表2所示。

表2 调查问卷部分题项

2)调查统计

问卷调研以线上调研为主。通过编写调研小程序向各方采集数据。鉴于调研内容专业性较高，特选取建设单位、施工单位、监理单位、风控单位以及安监站为主要发放单位，填写调查问卷的人员分布如表3所示，最终回收问卷232份，删去缺项以及不合格问卷，有效问卷为204份，有效问卷率为87.9%。

表3 调查对象个人背景情况分布

2.2.2 样本信效度分析

为检测数据样本的可靠性，在进行结构方程拟合前，使用SPSS v21.0对数据样本进行信效度分析，由Cronbach’sα系数表示数据样本的信度，KMO值表示数据样本的收敛效度[17]，结果如表4所示。各潜变量的Cronbach’sα均大于0.8，大于分界值0.7，说明数据样本信度良好，数据内部一致性高，数据可靠；同时，各潜变量的KMO值均大于0.7，P值均为0.000，通过0.05的显著性检验，说明各潜变量的收敛效度良好，数据之间相关性显著，测量模型可信度高。

表4 信效度分析

2.2.3 模型拟合

结构方程通常以卡方/自由(χ2/df)、近似误差平方根(RMSEA)、拟合优度指数(GFI)、调整拟合度指标(AGFI)、递增拟合指数(IFI)、比较拟合指标(CFI)、Tucker-Lewis指数(NNFI) 、均方根残差(RMR)8个指标检验模型适配度[18]，检验结果如表5所示，均在可接受范围之内。

表5 拟合结果

通过对模型的修正与模拟，得到最终地铁车站深基坑施工风险性测度结构方程模型，各潜变量与测量变量的路径系数如图4所示。由图4得知，在考虑各系统耦合作用下，基坑支护、基坑开挖、周边环境、降水排水与深基坑风险后果的相关系数分别为0.26，0.34，0.21，0.24，因此可知基坑开挖为主要影响因素，次之为基坑支护，而周边环境影响最小。同时，基坑开挖、基坑支护与降水排水三者耦合作用较高，相关系数分别达到0.73，0.59，0.64，这是因为地铁车站深基坑施工难度高、施工工艺复杂，基坑开挖、基坑支护与降水排水交替进行，相互影响。其中，基坑支护作业可靠性影响基坑开挖顺利进行，而基坑支护作业又以紧前开挖作业基本完成为前提。同时，为了保证基坑支护的稳定性与基坑开挖的顺利进行，还必须配置合理的降水排水作业来维持水土压力平衡与作业面的干燥，因此三者耦合作用较强。而基坑支护、降水排水与周边环境耦合作用较低，相关系数大多低于0.5，这是因为此工程周围建筑物与管线分布较少，使得周边环境与各潜变量耦合度都相对较低。

图4 标准化估计结果

根据路径分析，求得各风险因素的标准化系数作为权重大小，如表6所示。潜变量基坑支护的主要影响因素为支护形式，其标准化估计值为0.85，这要求选用合理的支护形式和细化基坑支护参数非常重要；潜变量基坑开挖的主要影响因素为开挖技术参数设置，其标准化估计值为0.94，这要求在实际土方开挖作业中，应严格采用“开槽支撑、先撑后挖、分层开挖、严禁超挖”的开挖原则，并结合实际情况，严格按照专项施工方案管理办法落实；潜变量周边环境的主要影响因素为周边建筑物情况，其标准化估计值为0.88，这就要求工程实践中，要按照相关规范严格落实基坑施工动态监测工作，提前预警，有险必知；潜变量降水排水的主要影响因素为降水排水方法选用，其标准化估计值为0.83，应结合基坑附近水文地质情况，合理选取降水排水方法，并密切关注降水效果及对环境的影响。

表6 部分参数标准化估计值

内生潜变量除了受外生潜变量的影响之外，同时还受到人员伤亡、经济损失、工期损失3个测量变量的影响。根据路径分析可知，与风险后果的相关系数分别为0.84，0.74，0.71，均为正相关。权重系数相差不大，说明在深基坑施工过程中，发生人员伤亡的同时，往往伴随着经济与工期损失。

2.3 建立SEM-MC地铁车站深基坑施工危险性测度模型

根据结构方程正态性检验，所有风险因素都符合正态分布，使用Crystal Ball对数据分别进行批量拟合，得出各风险因素的分布参数；然后利用MC法对各个风险因素随机产生5 000个值，根据测量模型公式可以确定各潜变量模拟值的概率分布，如表7所示。

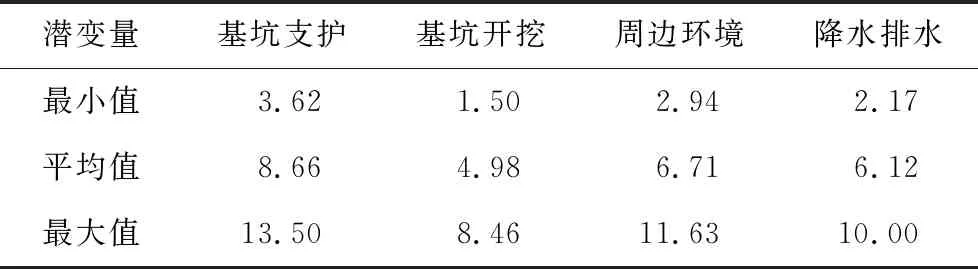
表7 潜变量模拟值

类似地，可依次得到其他潜变量的概率分布。依据式(1)，结合风险损失程度与风险因素权重得到新的危险性测度模型，最后生成危险度概率分布图，如图5所示。深基坑施工危险度服从μ=21.29，σ=3.42的正态分布，取均值R=21.29，由表1可得该地铁车站深基坑施工危险性等级为4级。该地铁车站基坑土质力学性能差，根据危险性测度研究成果可知开挖技术参数设置对施工安全影响较重，因此在施工过程应高度关注。同时，根据危险性等级加强日常风险管理，对相应风险进行防范，并采取预警措施，制定风险应急方案，将地铁车站深基坑施工危险性等级降为可接受水平。从实际效果看，该施工危险性测度成果较好的指导了深基坑施工，使工程施工更为高效、安全。

图5 危险度概率分布

3 结论

1)基于基坑支护、基坑开挖、周边环境、降水排水4个风险维度构建地铁车站深基坑危险性测度指标体系，运用风险耦合机理反映各个外部因素之间的相关关系及耦合作用，说明地铁车站深基坑风险是由各风险因素耦合所致。

2)结构方程模型充分考虑各风险因素之间的耦合作用，结合蒙特卡洛模拟方法建立的地铁车站深基坑危险性测度方法，降低了数据主观性影响，使风险测度结果更具科学性与有效性。

3)将结构方程-蒙特卡洛模拟方法运用于实际工程中，其风险评测结果为地铁车站深基坑施工安全管理提供较好的指导，有效避免了风险事故发生，提高风险管理的科学性与准确性，为地铁车站深基坑施工危险性评测提供了1种新方法。