切顶卸压自成巷的连续-非连续方法模拟及切缝倾角的影响*

2022-08-06刘天成王学滨岑子豪薛承宇

中国安全生产科学技术 2022年6期

刘天成，王学滨，岑子豪，杜轩，薛承宇

(1.辽宁工程技术大学力学与工程学院，辽宁阜新 123000；2.辽宁工程技术大学计算力学研究所，辽宁阜新 123000)

0 引言

沿空留巷技术[1-3]取消了传统的区段煤柱，使每条巷道服务2个工作面。切顶卸压自成巷技术通过在巷道顶板切缝，并利用矿山压力和岩体的碎胀特性实现无煤柱开采[4-11]，近年来得到了快速发展，具有煤炭采出率高、巷道掘进率低及作业安全性高等优势。

目前，科技人员多采用连续方法和非连续方法开展切顶卸压自成巷研究[12-13]。韩昌良等[12]采用FLAC3D分析了不切顶与切顶的差异，研究发现，卸压对最终采动应力的改善很小，但能大幅降低巷道变形量；高玉兵等[13]采用UDEC考察切缝倾角的影响，研究发现，切缝倾角偏小将造成矸石对切顶短臂结构产生向下的摩擦作用，且无法对其产生斜撑作用，而切缝倾角偏大将造成切顶短臂结构的重量偏大。所以，切缝倾角以10°～20°为宜。在UDEC中，块体尺寸被预先假定，且某些岩层的块体尺寸较大，这将导致开裂路径有限，从而不能很好地描述裂纹的时空分布。

连续方法虽在一定程度上适于模拟连续介质的变形、破坏问题，但一般不适于模拟非连续问题。非连续方法虽然适于模拟非连续问题，但对于应力和应变的描述较为粗糙。近些年来，连续-非连续方法应运而生，具有广阔的应用前景。

以作者自主研发的适于模拟连续介质向非连续介质转化或非连续介质进一步演化的拉格朗日元与离散元耦合连续-非连续方法为基础[14]，提出基于高斯求积公式的势接触力计算方法以提高计算效率，并模拟不同切缝倾角时柠条塔煤矿S1201工作面的切顶卸压自成巷过程。

1 原接触算法简介

为便于下文阐述，作如下定义和约定：若某条棱(单元的边)被2个单元所拥有，则称为内棱；若仅被1个单元所拥有，则称为外棱；若某个节点被某条棱所拥有，则称该棱为该节点的关联棱；若某节点的关联棱均为内棱，则称该节点为内节点，否则称为外节点；若某单元所拥有的节点均为内节点，则称该单元为内单元，否则称为外单元；将计算模型所在空间划分为尺寸一致的正方形网络，称每个网格为盒子。

拉格朗日元和离散元耦合的连续-非连续方法包括4个模块：应力-应变模块、开裂模块、接触-摩擦模块和运动模块。其中，接触算法[15]是基于势接触理论。

在原接触算法中，采用单元-单元接触模式。该算法包括接触检测和接触力计算2个部分。在接触检测部分，在每个盒子内，通过判断每2个外单元是否存在相交的外棱实现嵌入判断，需进行大量的矢量计算。在接触力计算部分，对于每2个相嵌入的外单元，通过计算势函数在其互嵌区域边界上的积分求得接触力，并将该接触力分配至相应节点。其中，势函数在积分域上分段线性，为此，需确定各区段端点位置并计算它们的势，这导致计算效率低下。

2 基于高斯求积公式的势接触力计算方法

2.1 接触检测

在本文提出算法中，采用点-单元接触模式。在每条外棱上布置4个接触点，其编号i为1～4，其位置矢量ri满足式(1)：

(1)

式中：r0和r5分别为每条外棱上两端外节点的位置矢量；xi为4点高斯-勒让德求积公式的求积节点，-x1=x4≈0.861 1，-x2=x3≈0.340 0。

将所有接触点和外单元加入盒子。对每个盒子内的接触点和外单元两两进行嵌入判断。当某一接触点P嵌入某一外单元γ时，称P与γ的组合为1个接触对。

提出算法的优势在于：P只会被加入1个盒子。所以，涉及P的接触对只生成于该盒子的嵌入判断，而不会有重复的接触对生成。

2.2 接触力计算

γ上的势函数φ(P)与原算法中的一致，如式(2)所示：

(2)

式中：Kn为法向接触刚度，Pa/m；h(P)为点P到γ边界最短距离函数。

对于每个接触对，P上的接触力F如式(3)所示：

F=0.5KnLAihn

(3)

式中：L为P所在外棱长度，m；Ai为4点高斯-勒让德求积公式的求积系数，A1=A4≈0.347 9，A2=A3=1-A1；h为P到γ边界的最短距离，m；n为垂直于P所在外棱的单位矢量，方向指向P所在单元内部。根据静力等效原则，将F分配至P所在外棱两端外节点，并将F的反力分配至γ的4个节点。

提出算法的优势在于：通过采用4点高斯-勒让德求积公式计算势函数在2个外单元互嵌区域边界上的积分，提高了计算效率。

应当指出，提出算法是以4个求积节点为例进行阐述，易被推广至求积节点更多的情形。随着求积节点的增多，该算法的精度将逼近原算法的精度。

2.3 算法检验

模型由上部正方形块体和下部矩形块体2部分构成，如图1所示，二者间距为0。上部正方形块体边长为0.04 m，被剖分为20×20个正方形单元。下部矩形块体长度为0.2 m，高度为0.09 m，被剖分为100×45个正方形单元。正方形块体上边界受到0.1 MPa的压应力，矩形块体下边界被施加法向约束。无重力作用，计算在平面应力、大变形条件下进行。各种计算参数取值：Kn取1×1010Pa/m，面密度ρ取2 700 kg/m2，摩擦系数f取0.1，时间步长Δt取7.794 2×10-7s，局部自适应阻尼系数α取0.2，弹性模量E取1 GPa，泊松比μ取0.2。

图1 2块体接触过程

图1(a)给出了正方形块体下边界受到的平均法向接触力随时间t的演变规律；图1(b)给出了模型平衡后垂直应力的分布，正、负分别代表拉应力、压应力。由此可发现：在接触过程中，正方形块体下边界受到的平均法向接触力存在一定的波动，随着t的增加，波动幅度逐渐减小，直至保持4 000.34 N不变，这与理论值4 000 N相一致。由此说明本文提出算法具有较高的计算精度。另外，正方形块体的垂直应力分布基本均匀；对于矩形块体，接触面附近挤压严重，远离接触面的上边界的垂直应力为正，这与常识相符。

3 切顶卸压自成巷过程模拟

3.1 计算模型及方案

模拟不同切缝倾角θ时柠条塔煤矿S1201工作面的切顶卸压自成巷过程。采场的具体布置及巷道支护方式等内容参见文献[16]。采用锚杆进行原始支护。采用恒阻锚索进行补强支护，采用液压支柱进行临时支护。

模型长度为300 m，高度为80 m，被剖分为600×160个单元，工作面推进方向垂直于纸面。以模型左下角为原点O，水平向右为x轴正方向，竖直向上为y轴正方向，模型的左、右及下端面被施加了法向约束，如图2所示。该模型共包含7个岩层，其中石英砂岩层和粉砂岩层被剖分为四边形单元，而其他岩层被剖分为正方形单元，边长为0.5 m。各岩层参数见表1，表中数据主要取自文献[16]。

图2 巷道开挖后、煤层开挖前的计算模型

表1 各岩层参数

为避免四边形单元不能进一步开裂可能带来的高应力问题，对于煤层和脱离岩层的单元，采用文献[17]的基于应力球量不变假设的应力跌落方法处理，即当其应力状态满足莫尔-库仑准则时，将其应力从初始屈服面跌至残余屈服面。煤层和脱离岩层的单元的应力跌落系数β分别取为0.25，0.99。应当指出，在计算过程中，不允许煤层单元开裂，即将其视为连续介质，而对于其他单元，在脱离岩层前后，介质由连续介质向非连续介质转化，煤层与脱离岩层单元的β取值有所差异。对于脱离岩层的单元，β取值较高是为了避免对采场的过大扰动。

其他参数：Kn取为2个相接触单元的弹性模量E均值的10 m-1倍，f取0.3，重力加速度g取9.8 m/s2，α取0.5，2个岩层间界面黏聚力峰值取为其黏聚力c均值的0.77倍。计算在平面应变、大变形条件下进行。

计算过程：当时步数目N=0～5 000时，模型逐渐达到静力平衡。模型的上端面被施加了2 MPa的压应力，以模拟80 m厚的上覆岩层[16]。随后，开挖2条巷道，左巷为辅运巷，右巷为胶运巷，宽度均为6 m，高度均为4 m；左巷左壁的x坐标为77 m，2条巷道之间留有宽25 m的煤柱。

当N=20 000时，对右巷进行支护，如图3所示。将部分煤岩的强度参数提高0.5倍，以近似模拟锚杆的支护作用。共有2个锚杆支护区域，分别为煤帮2 m宽的范围和顶板2 m高、6.5 m宽的范围。在巷道顶板上施加2个相对的集中力，以近似模拟单列锚索的支护作用。共有2列锚索，锚固力分别为0.087 5 MN(左)和0.35 MN(右)。在巷道顶、底板表面的局部施加相对的应力，其与液压支柱的变形量(即顶、底板高度差的变化量)呈线性关系，系数为2 GPa/m，以近似模拟单列液压支柱的支护作用。共有2列液压支柱，初始值(初撑力)分别为0.206 MPa(左)和2.52 MPa(右)，最大值(工作阻力)分别为0.7 MPa(左)和4.44 MPa(右)。应当指出，为了直观研究左巷的破坏，不对左巷进行支护。

图3 右巷支护情况

当N=35 000时，在右巷的右上角切缝。切缝高度取为9 m。设计5个计算方案：θ分别取0°,5°,10°,15°，20°。

当N=50 000～950 000时，以逐渐卸压的方式开挖右巷右侧的煤层，共计186 m。

3.2 方案3的结果及分析

θ=10°时(方案3)最大主应力σ3及裂纹区段的时空分布如图4所示，正、负分别代表拉应力、压应力，灰色和黑色线段分别代表拉裂纹区段和剪裂纹区段[18]。

由图4(a)可知，当N=40 000时，巷道的开挖、支护及切缝均已完成，回采尚未开始。两巷的顶、底板均出现了垂直拉裂纹，相比之下，右巷顶板的裂纹更少，这是由于对右巷进行了支护；切缝尖端出现了σ3集中，且由此发育出了少量的拉裂纹；煤体发生了局部破坏，煤体的应力分布不连续。

由图4(b)～图4(d)可知，当N=120 000～800 000时，右巷右侧的煤层的顶、底板处于逐渐卸压状态。若干岩层出现了越来越多的拉裂纹和剪裂纹，并向下运动；切缝尖端发展出了较长的低角度拉裂纹，并逐渐向右上方发展。应当指出，当N=240 000时，左巷直接顶拉裂纹附近已发展出了一定数量的剪裂纹。

由图4(e)～图4(f)可知，当N=1 000 000～1 200 000时，采空区已形成。由切缝尖端发展出的低角度拉裂纹促进了采空区上方部分岩层冒落，模型上表面出现了明显下沉；左巷顶板发生了少量冒落。

方案3的煤体支承压力-x曲线如图5所示。支承压力是指初始中心纵坐标为16.75 m的一行煤层单元的垂直应力的绝对值。由图5可以看出，左侧煤层和煤柱的支承压力的峰值不位于二者的边缘，这意味着它们均发生了破坏。应当指出，煤柱的支承压力分布呈单峰特性，这意味着煤柱已完全破坏。

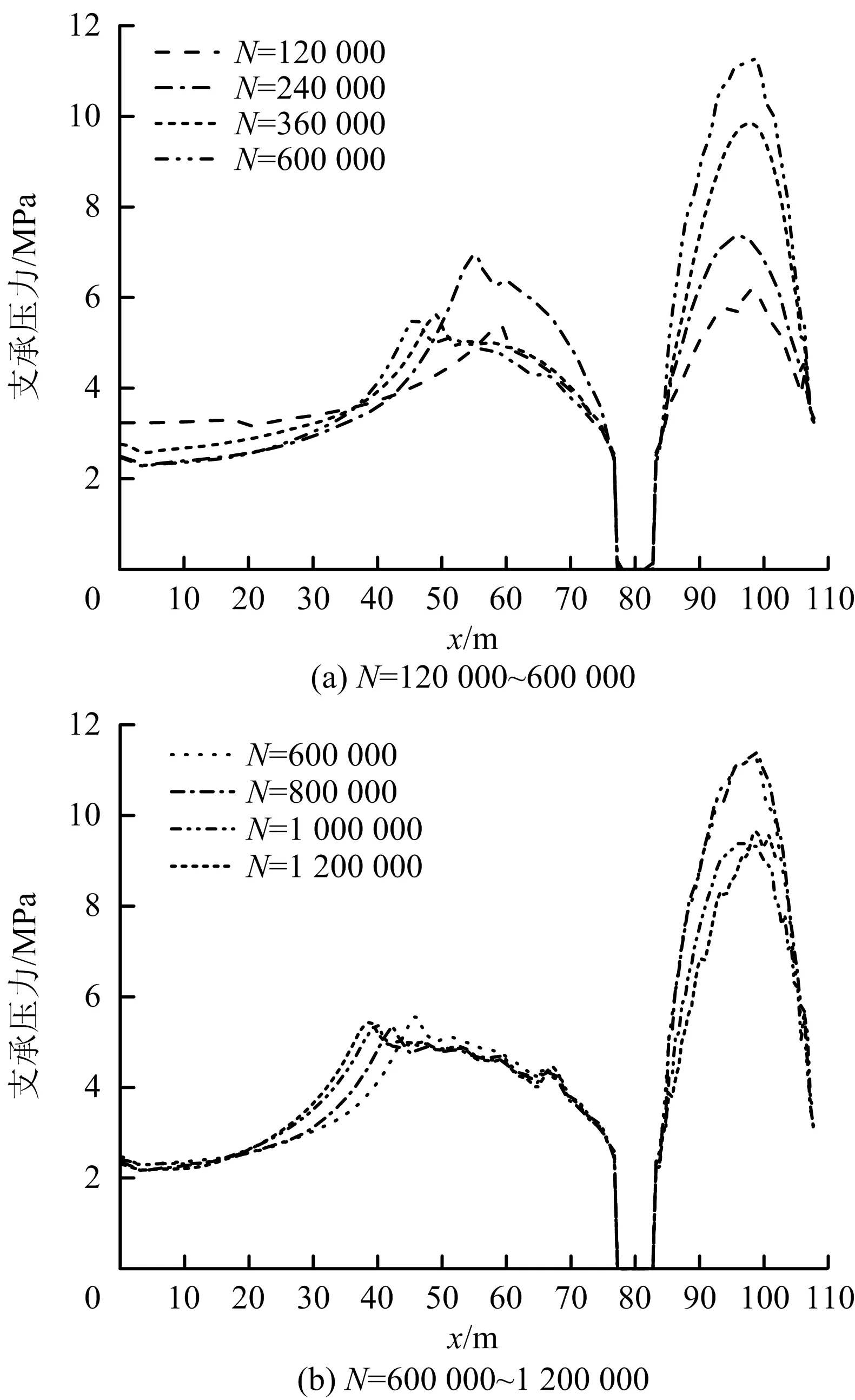
图5 煤体的支承压力-x曲线(方案3)

对于左侧煤层，当N=120 000～240 000时，支承压力的峰值左移，这是由于向煤层转移的岩层压力使其破坏区尺寸增大；支承压力的峰值增加，这是由于越接近模型左边界σ3(围压)越大。

对于左侧煤层，当N=240 000～1 200 000时，支承压力的峰值减小，这是由于左巷上方逐渐扩展的裂纹阻隔了岩层压力向左传递(图4(c))。另外，支承压力的峰值左移。众所周知，煤层右部岩层压力的降低将引起其与顶、底板摩擦力的降低，这将导致煤层的围压有所释放，进而导致支承压力的降低。若出现煤层的支承压力不足以抵抗岩层压力的情况，则支承压力峰值会左移。

图4 σ3及裂纹区段的时空分布(方案3)

对于煤柱，当N=120 000～800 000时，支承压力总体上升，这可能是由于对煤层单元进行了应力跌落，σ3(围压)有所提高。

对于煤柱，当N=800 000～1 200 000时，支承压力总体下降，这是由于采空区形成前后，部分岩层垮落导致了煤柱的部分应力转移至底板。

3.3 θ的影响

N=1 200 000时方案1～2和方案4～5的σ3的分布如图6所示，具体含义同第3.2节。由图6可以看出，θ越大，右巷顶板的完整性越好，这是由于当θ较大时切缝尖端发展出的裂纹促进了采空区顶板冒落，从而阻隔了岩层压力向右巷顶板传递；θ越大，左巷顶板的冒落越严重，甚至，在方案5中，左巷已被冒落的岩块填满；θ=0～5°时，左巷上方裂隙较发育，这说明岩层压力向左传递未被较好地阻隔住。综合考虑，θ以10°为宜。

图6 方案1～2和方案4～5的σ3及裂纹区段的分布(N=1 200 000)

N=1 200 000时方案1～5的煤体支承压力-x曲线如图7所示。由图7可以看出，当θ=0～10°时(方案1～3)，支承压力-x曲线基本一致；当θ=15～20°时(方案4～5)，煤柱中部的支承压力-x曲线呈上凹，且θ越大，煤柱中部的支承压力越低，煤柱两帮和左巷左帮的支承压力越高。

图7 方案1～5的煤体支承压力-x曲线(N=1 200 000)

当θ较大时，右巷顶板悬露的岩层尺寸较大，使煤柱正上方的直接顶呈上凸的拱形，这会使本应向煤柱中部传递的较大岩层压力向别处转移。自然地，左拱角对左巷的直接顶会产生额外的水平方向岩层压力，这将使该处发生大规模剪裂，进而严重冒落。与此同时，左巷中冒落的岩块会对左巷两帮产生一定的围压，这会提升两帮的支承压力。