未标定的视频小卫星深空目标凝视控制
2022-08-06范才智王猛猛
宋 超,范才智,王猛猛
(国防科技大学 空天科学学院, 湖南 长沙 410073)
在天文观测等场景中对深空目标观测时需要对目标进行稳定持续的高精度凝视。视频卫星因其能够对观测目标实现连续的跟踪并且获取视频信息,使得它在持续目标跟踪场合有着得天独厚的优势。在轨的视频卫星有诸如国内的吉林1号[1]、天拓2号[2]以及国外的LAPAN-tubsat[3]等。利用视频小卫星实现目标凝视跟踪通常可分为基于位置信息和图像信息的凝视控制两种方法。
传统的基于目标位置信息的凝视控制[4-5],首先根据目标先验位置信息设计出稳定凝视时卫星的期望姿态,然后通过比例微分(proportion differentiation, PD)控制等方式实现姿态的机动和跟踪。然而,目标位置信息未知的情况下,基于给定目标位置的传统凝视控制方法并不适用。
基于相机图像信息的凝视控制方法不需要目标的位置信息,利用现代图像识别技术[6-8]提取出观测目标在像平面中的像素坐标,然后利用该像素坐标与期望坐标之间的误差进行反馈控制卫星。由于目标在惯性空间中的位置速度并不可知,控制器若要根据目标成像的像素坐标将其控制到期望的图像中的位置,一般需要根据相机的内外参数,将像素偏差转换为当前姿态与期望姿态之差,然后设计合适的控制律使得姿态误差收敛,最后间接实现将目标成像移动到像平面中期望的位置[9-10]。但是该方法需要依赖准确的相机参数才能实现有效跟踪控制。然而,卫星相机参数在长期的在轨运行过程中不可避免会发生变化,在轨标定相机内外参数十分困难。
基于未标定相机进行视觉伺服控制在机器人[11-14]、无人机[15-20]等领域有许多的研究工作,但目前尚未有针对未标定的视频卫星跟踪控制的研究工作发表。
本文针对深空目标位置信息未知条件下的观测任务,提出了一种基于未标定相机图像反馈的自适应控制方法。该方法能够对相机参数和目标位置进行在线估计,使得目标在像平面的成像能控制到期望位置,并通过仿真验证该方法的有效性。
1 成像模型
1.1 假设条件
视频卫星针对深空目标进行观测,这类目标包括远距离的恒星或在观测期间可忽略相对运动的行星。因此假设在惯性空间中是静止的观测目标。
1.2 相机模型
1.2.1 相机内部模型
相机内部模型描述的是目标入射光线与像平面上的坐标之间的关系。最常用的是小孔成像模型,即入射光线穿过镜头中心到达镜头后方的传感器,然后传感器将光信号转换为电信号最后成为数字图像信息,如图1所示。
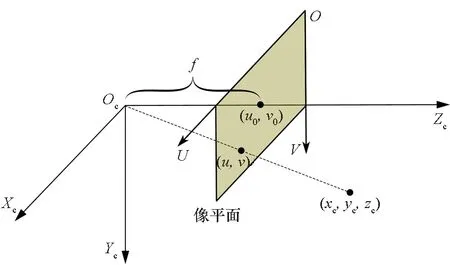
图1 相机内部模型Fig.1 Intrinsic camera model
定义相机坐标系为Oc-XcYcZc,其中:原点Oc位于镜头中心,即小孔成像的光线交叉中心;Zc轴由相机内部指向外部并且垂直于像平面;Xc轴和Yc轴与矩形像平面对应的边平行,并与Zc轴形成右手坐标系。二维像平面O-UV与Zc轴垂直,原点O位于传感器的顶点,两条轴分别沿着传感器相互垂直的两条边。设f为焦距,相机坐标系原点Oc到目标点T的矢量为RcT,其在相机坐标系中的坐标表示为cRcT=[xc,yc,zc]T,左上标的c表示其为在相机坐标系的分量,以此类推。而T在像平面的成像坐标为(u,v),镜头中心光轴与像平面的交点为像平面中心(u0,v0)。传感器由众多像素组成,假设像素的物理尺寸为dx×dy。根据投影的相似原理,有:
(1)
变换后得到:
(2)
式(2)引入了齐次坐标便于坐标变换的表示,并建立了由相机坐标系向像素坐标的转换关系,其中定义矩阵:
(3)
1.2.2 相机外部模型
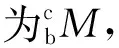
(4)

图2 相机外部模型Fig.2 Extrinsic camera model
由此可以得到cRcT与bRbT的关系为:
(5)
结合式(2)和式(5),目标在体坐标系的位置到像素坐标的映射关系为:
(6)
式中,N为投影矩阵,N=Π·T。
1.2.3 卫星与目标相对位置模型

(7)
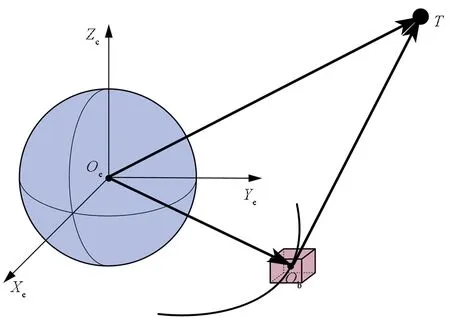
图3 卫星与目标相对位置模型Fig.3 Relative position model of the satellite and the target
观测目标在地心惯性坐标系中的位置与其在体坐标系中的表示的关系为:
(8)
结合式(6)和式(8),可以得到观测目标在地心惯性坐标系中的位置与其成像的映射关系:
(9)
1.2.4 投影模型

(10)
定义目标在像平面的成像的坐标为y(t)=[u(t),v(t)]T,则还能得出y(t)和深度zc(t)的表达式分别为:
(11)
(12)
2 运动学与动力学
2.1 卫星姿态运动学与动力学
采用刚体模型描述卫星的姿态。定义姿态四元数q:
q=cos(φ/2)+rsin(φ/2)=q0+qv
(13)

(14)
式中,E3代表3×3的单位矩阵,J为卫星转动惯量,ω是卫星相对惯性坐标系的转动角速度在体坐标系下的表示,U是控制力矩,(·)x算子表示的操作如下:
(15)
2.2 相机成像运动学
需要指出的是,观测目标可视为静止,即iReT为时不变,利用此特性对式(11)~(12)求导得到:
(16)
假设观测的目标的距离远大于卫星的轨道半径,即:
iReT≫iReb(t)
(17)
根据式(17)可简化矩阵Th和式(11)中的轨道运动相关项,像素坐标和深度的运动学方程相应简化为:
(18)
3 参数估计
3.1 估计参数定义
从相机模型以及成像运动学方程可以观察到,存在未知的时不变投影矩阵N和目标位置iReT,其都会对成像的精度产生影响。参数识别的目的在于用估计的参数实现与准确参数值一样的控制效果。实现方式是设计参数的自更新律,使得依赖于估计参数值的控制器能够将图像误差收敛至零。值得指出的是,图像误差收敛于零并不一定意味着参数的估值也收敛于实际值。
(19)
式(19)中的N(3)和iReT是以乘积的形式同时出现的。进一步分析式(11)有:
(20)
与式(19)相比,N矩阵的最后一列元素n14、n24和n34是单独出现的,并没有与iReT的元素相乘。所以综合得出需要估计的参数为:
θ=[nijxk,n14,n24,n34]Ti,j,k=1,2,3
(21)


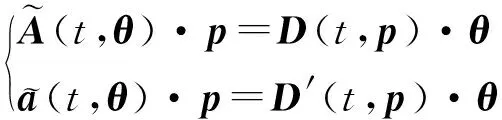
(22)
θp(t)=[nijxk,n31x1,n31x2,n31x3,n32x1,
n32x2,n32x3,n33x1,n33x2,n14,n24,n34]T
i=1,2,j;k=1,2,3
(23)
3.2 估计投影误差
(24)
性质2对于投影估计误差e(t),可以找到矩阵Wp(t)∈R2×n,使得:
e(t)=Wp(t)Δθp(t)
(25)
根据式(23)给出的参数定义,式(24)中的参数都以线性的形式出现在e(t)表达式中,所以性质2显然成立,不再给出证明。
3.3 势函数设计
定义图像跟踪误差Δy(t):
Δy(t)=y(t)-yd
(26)
式中,yd为目标期望的成像坐标。定义矩阵G(t)∈R3×2:
(27)

(28)
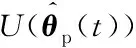
(29)
值得指出的是,即使在式(29)作用下的势函数收敛于局部极小值,其对应的G(t)的行列式也不为零,所以势函数的局部极小值问题并不妨碍其起到预期的作用。
3.4 估计参数更新
根据定义的参数估计误差以及投影误差,设计如式(30)所示的参数自更新律。
(30)
式中,矩阵Yp(t)的定义将在下一节控制器设计部分给出,Γ∈R29×29,K1∈R2×2和K2∈R29×29为正定对角系数矩阵。
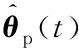
4 自适应控制器设计
设计控制器如式(31)所示。
U(t)=ω(t)×Jω(t)-K3ω(t)-
(31)
式中,K3、B、K4均为正定对角系数矩阵。
为了研究给定控制器的稳定性,首先定义三个函数:
(32)
V1(t)和V3(t)显然都是非负的。zc(t)由于是目标在相机坐标系Zc轴上的分量,考虑到目标出现在视场内时,其深度zc(t)必然为正数,所以V2(t)也是非负函数。分别对V1(t)、V2(t)、V3(t)求导:
(33)
进一步地,定义李雅普诺夫函数V(t):
V(t)=V1(t)+V2(t)+V3(t)
(34)
取更新律(30)的矩阵Yp(t),使其满足:
(35)
则代入式(33)后求得V(t)的导数为:
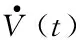
(36)
设k4min为K4的最小特征值,k2max为K2的最大特征值,τmin为Γ的最小特征值。k4min满足:
(37)
则此时,
(38)
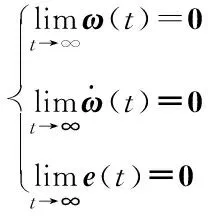
(39)

(40)
在式(27)中定义了矩阵G(t),并且通过设计的势函数保证G(t)的秩始终为2。根据式(40),对任意的G(t),G(t)BΔy(t)都趋近于零,所以有:

(41)
在参数更新律(30)和式(31)的作用下,成像误差、凝视时的角速度、估计投影误差都收敛为零,说明能够在相机参数以及远距离静止目标位置都不确定的情况下,将目标在像平面中的成像坐标保持在期望的位置,实现稳定的凝视跟踪。
5 仿真分析
仿真中假设目标初始状态已经处于视野中,然后利用本文的控制算法将目标控制到期望位置。相机参数如表1所示,其中M321(·)表示按照3-2-1转序转动对应角度的旋转矩阵。相机参数的理论值表示仿真中设置的理论相机模型参数,实际值是表示各种因素产生偏差后相机实际的参数,用于仿真中计算观测到的目标在像平面中的目标y(t)。

表1 相机参数Tab.1 Camera parameters
表2为仿真时控制器中所用到的各个系数值,其中diag{·}表示将其中各个元素依次作为对角线上的元素,其他空置位置均为0的矩阵。

表2 控制参数Tab.2 Control parameters
像平面大小为752像素×582像素,观测目标为远距离天体,当识别到的目标出现在视场边缘时,自适应控制器开始介入并将目标位置控制到期望的视场中心位置(376,291)像素坐标处。
图4是识别到的观测目标在视场中的成像轨迹。目标初始在像平面的位置位于视场的边缘角落,在控制器的作用下沿着图示轨迹运动到视场中心位置,说明控制器达到期望的效果,这样的位置有利于获得更好的凝视观测图像。图5展示了不同时刻下目标实际像素坐标与期望坐标之间的误差曲线,说明了像素误差在u、v两个方向上都逐步实现了收敛,与预期效果一致。图6则是表征参数识别效果的估计投影误差e(t)的变化曲线,由于参数的更新从而使得e(t)能够收敛为零,说明未标定的相机参数对成像的影响降到最小。仿真结果表明控制器能够达到预期的控制目标,使得目标成像在期望的视场位置。
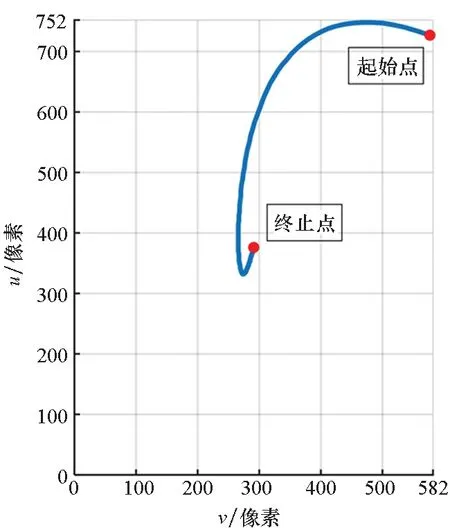
图4 目标在像平面的成像轨迹Fig.4 Target track on the image plane

图5 图像跟踪误差Δy(t)曲线Fig.5 Curve of image tracking errors Δy(t)
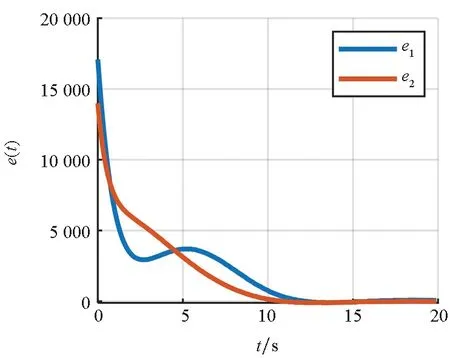
图6 估计投影误差e(t)曲线Fig.6 Curve of estimated projection errors e(t)
6 结论
本文针对视频小卫星对深空目标观测任务中目标位置与相机内外参数都未知的情况,基于深空目标近似作为惯性空间静止目标的假设条件,设计了一种深空目标凝视自适应姿态控制方法。该方法引入了一个参数相关的势函数,使得参数矩阵的秩始终满足图像误差收敛的要求;据此采用了参数自更新律对未知参数进行在线更新,使得估计投影误差收敛;使用估计的参数设计了自适应凝视控制器,将目标投影在像平面的坐标控制到期望位置。利用李亚普诺夫理论和芭芭拉特引理严格证明了闭环系统的稳定性。数值仿真结果验证了设计的控制器的有效性。下一步的研究中,拟将该方法推广应用到近地空间目标跟踪场合。
