月壤参数对月面着陆气囊缓冲性能的影响
2022-08-06周仕明李道奎
周 旋,周仕明,李道奎
(1. 国防科技大学 空天科学学院, 湖南 长沙 410073; 2. 空天任务智能规划与仿真湖南省重点实验室, 湖南 长沙 410073)
月球是世界各国开展深空探测的首选目标。随着探测的不断深入,月面活动已进入新的阶段。2020年10月,以美国为首的7个国家签署了《阿尔忒弥斯协定》,计划对月球上矿产资源进行开采。2021年6月,中国和俄罗斯联合发布了《国际月球科研站合作指南》,诚邀国际合作伙伴在月球上建设科研基地。无论是进行矿产开采还是建立月球基地,都必然有大量的物资需要投送到月球上。相对于软着陆机构和空中悬吊机,气囊缓冲装置有着体积小、质量轻、成本低、结构简单、性能可调、稳定性好的特点[1],因而在物资的着陆缓冲方面更具优势和潜力。1966年,苏联的“月球9号”采用气囊装置实现了人类历史上第一次在月球表面的软着陆。后来,由于载人登月的需求,美国和苏联均转向研究软着陆机构。直到1997年,美国的火星“探路者号”才再次使用气囊装置实现了火星表面的软着陆。因为优势明显且无须返回地球,此后,气囊装置在行星(火星、水星等)探测上的应用越来越多[2-3]。因此,无论是从发展趋势,还是从技术可行性的角度来看,气囊装置都将再次被用于月面着陆缓冲。此外,由于大载重的需要,密闭型气囊不再适用(“月球9号”气囊为密闭型气囊),随着气囊技术的发展,排气型气囊(包括组合型气囊)将被采用。
相对于地球,月球环境有其独特性。除了月球重力加速度小、基本无大气外,月壤的力学性能(抗剪性、承载力等)也有着明显不同[4]。普遍认为月壤较松软,因此,必须分析月壤对月面着陆气囊缓冲性能的影响。1966年,Jaffe和Scott[5]对“月球9号”气囊在3种月壤下缓冲后的下陷深度进行了计算。之后由于气囊再未被用于月面着陆,因而未见关于月壤影响气囊缓冲性能的研究。对于地面着陆气囊的缓冲分析,大多将土壤简化为刚体[6-7],对于硬土壤这种假设是可行的。但是,对于软土壤(如黏土、沙土等)或重载的着陆缓冲,则必须考虑土壤的力学特性。Taylor等[8]在分析重装空投气囊的着陆缓冲时建立了土壤模型,但没有给出土壤对缓冲性能的具体影响。对此,连伟欣等[9]分析了不同地面的影响,结果表明相对刚性地面模型,土壤地面模型的最大竖直过载减小了约22%。高浩鸿等[10]在进行无人机回收气囊缓冲试验时发现,地面越松软,气囊的缓冲性能越好。可见,土壤特性对气囊缓冲性能的影响显著;而月壤相对较软,影响会更大。
火星土壤与月壤类似[11],都属于砂性土壤,所以在研究火星着陆气囊时均会考虑土壤特性[12-13]。Timmers等[14]在分析猎户座乘员舱的气囊着陆系统时,发现土壤越软、越湿润,气囊下陷得越深,甚至会导致乘员舱撞击地面。因而,Tutt等[15]讨论了两种土壤下猎户座乘员舱气囊缓冲的鲁棒性。为避免单因素实验设计的缺点,DeLoach[16]采用现代实验设计的方法,系统地研究了不同类型土壤对气囊缓冲性能的影响。此外,Heymsfield等[17]计算了无气囊的应急着陆工况下土壤参数对猎户座乘员舱所受冲击加速度的影响大小。同样地,对于月面着陆气囊不仅需要研究不同月壤对其缓冲性能的影响,也需系统地分析月壤参数的影响规律。
土壤的计算模型很多,主要有双线性模型、等效线性模型、黏弹性模型、理想弹塑性模型和可压溃模型等[18],特别是后两种模型在土壤冲击模拟、软着陆机构的着陆缓冲、返回舱着陆等领域中应用最多[19-21]。LS-DYNA软件中提供了一种可压溃的泡沫模型,其能够综合考虑土壤的弹性、可压缩性及其特殊的屈服特性[21],被广泛应用于猎户座乘员舱着陆气囊的缓冲动力学建模与分析中[14-17,22]。因此,本文也将采用该模型对月壤进行建模。
针对上述问题,本文设计了圆柱形的月面着陆气囊,并基于可压溃泡沫模型建立了考虑月壤特性的气囊缓冲动力学模型,分析了不同月壤下的气囊着陆缓冲过程,研究了月壤参数对着陆气囊缓冲性能的影响,以期为气囊的结构设计、月壤对气囊缓冲性能影响的评估及月面着陆点的选择等提供参考。
1 模型的建立与验证
考虑土壤特性的着陆气囊缓冲动力学有限元模型包括气囊和土壤两部分。同时建立这两部分的有限元模型,然后在LS-DYNA软件中通过自动面面接触算法(关键字*CONTACT_AUTOMATIC_SURFACE_TO_SURFACE)定义气囊与土壤、有效载荷与土壤之间的接触关系,即可完成最终建模。下面分别对气囊和土壤的建模方法进行说明并验证。
1.1 气囊有限元建模及验证
建立气囊缓冲有限元模型的方法主要有两种:控制体积法(control volume, CV)和任意拉格朗日欧拉法(arbitrary Lagrange-Euler, ALE)。对于折叠气囊的展开过程,ALE法能够较为准确地模拟,对于气囊缓冲过程这两种方法的计算结果基本一致,但CV法的计算效率更高[6]。因此,选择CV法对气囊的缓冲过程进行模拟。
根据气体状态方程,有
P=(γ-1)ρgase
(1)
式中,P为气囊内压,γ为气体比热比,ρgas为气囊气体密度,e为气囊气体比内能,且有
(2)
式中,V为气囊气体体积。
联立式(1)和式(2)即可得到气囊内压P与气体体积V的关系。CV法通过对曲面积分来计算气囊体积,即
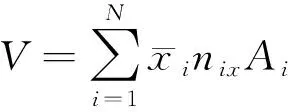
(3)
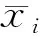
气囊排出气体的质量流量为
(4)
式中,Cor为排气口系数,Aor为排气口面积,Rgas为个别气体常数,T为气囊气体温度,λ为排气口上下游压力之比,且有
(5)
式中,Patm为环境压力。
基于上述着陆气囊的缓冲动力学建模方法,对文献[23]中圆柱形气囊的着陆缓冲试验过程进行仿真分析。有效载荷质量为2.5 kg,冲击速度为4.8 m/s,建立其有限元模型如图1所示。气囊是通过织物拼接而成,在建模时进行了简化,忽略缝合线的影响,并且未建立实际的排气口而是设置了虚拟排气口。上述简化对计算结果影响很小,在仿真分析中被广泛采用[7-9,24]。试验时的地面为室内的水泥地面,因此通过刚体来进行模拟。有效载荷也定义为刚体。在LS-DYNA软件中通过自动面面接触算法定义气囊与有效载荷之间的接触关系,通过关键字*CONTACT_AIRBAG_SINGLE_SURFACE定义气囊的自接触属性,通过关键字*CONSTRANED_EXTRA_NODES_SET定义气囊与有效载荷之间的绑定关系。气囊织物的厚度为0.16 mm,将织物看作是各向同性材料,弹性模量为300.0 MPa,泊松比为0.2[24]。
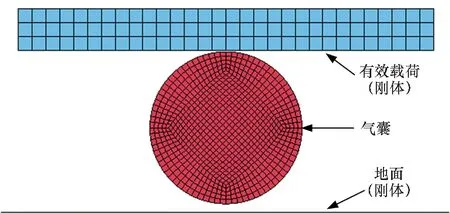
图1 着陆气囊的有限元模型Fig.1 Finite element model of the landing airbag
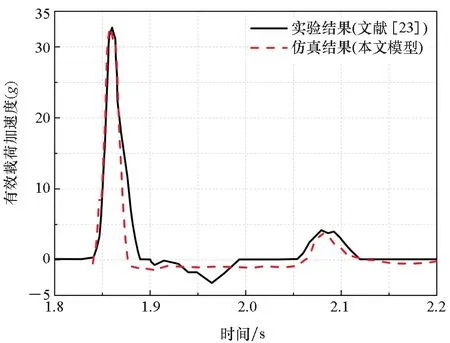
仿真与实验结果对比如图2所示,可以看到,两者的一致性好,且气囊峰值压力和有效载荷最大加速度的相对误差均小于1.0%,这表明着陆气囊的缓冲动力学建模方法合理可行。
(a) 气囊内压(a) Airbag pressure
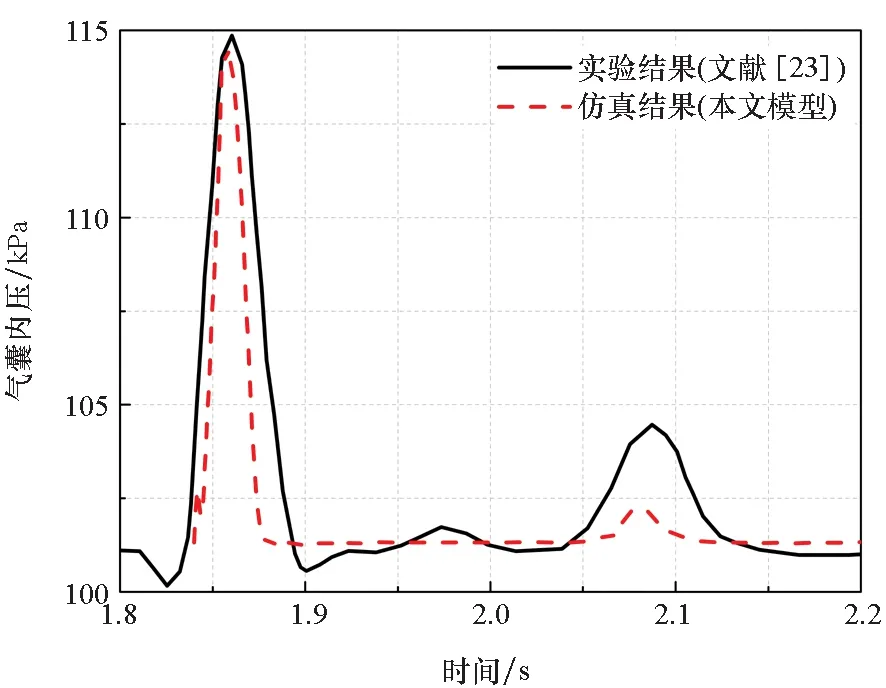
(b) 有效载荷加速度(b) Payload acceleration图2 着陆气囊的仿真与实验结果对比Fig.2 Comparison of simulation and test results of the landing airbag
1.2 土壤有限元建模及验证
着陆冲击过程一般很短,产生的冲击波所影响的土壤面积有限。仿真计算时,为降低计算成本、提高分析效率,往往通过建立有限大的土壤模型,并施加无反射边界条件来模拟无限大的真实着陆地面[21]。采用波速法可以计算得到着陆冲击过程中土壤受影响的深度[25],即
(6)
式中,D为影响深度,tp为前沿时间,vs为剪切波速。
可压溃泡沫模型主要用密度ρ、剪切模量G、体积模量K、屈服函数φ和拉伸破坏截止压力Pc等参数对土壤进行描述。其中,冲击下的剪切模量可根据强夯土壤的剪切模量约为小变形剪切模量的1/10[25]或剪切波速[26]得到;体积模量可根据泊松比求得;因为土壤基本不能承受拉伸,因此拉伸破坏截止压力设为很小的负值(负值表示受拉);屈服函数φ可用第二应力不变量J2、静水压力p,以及屈服参数a0、a1、a2来表示,即
φ=J2-[a0+a1p+a2p2]
(7)
(8)
那么
J2=a0+a1p+a2p2
(9)
对于屈服参数a0、a1、a2,目前无法通过试验测得,但可利用Drucker Prager模型进行初值估计,其表达式为
(10)
其中
I1=σii=σ1+σ2+σ3=-3p
(11)
(12)
(13)
式中,I1为第一应力不变量,α和k是土壤摩擦角φ和内聚力c的函数。
联立式(10)和式(11),可得
J2=k2+6αkp+9α2p2
(14)
对比式(9)和式(14),有
(15)
根据土壤力学参数的变化范围,通过上述计算即可得到泡沫模型中各参数的取值范围。
对文献[27]中的土壤冲击实验进行仿真模拟,有限元模型如图3所示,落体是直径为0.408 m的金属半球,质量为12.05 kg,定义为刚体;土壤模型尺寸为0.5 m×1.0 m×1.0 m[26],底面固定。土壤类型为硬土,其特性参数如表1所示,根据式(15)可求得屈服参数a0、a1、a2。金属半球的冲击速度为34.97 m/s,仿真与试验结果对比如图4所示,可以看到两者吻合得较好,最大冲击加速度的误差小于3.0%,验证了所建模型的有效性,表明可压溃泡沫模型能够很好地模拟土壤特性。
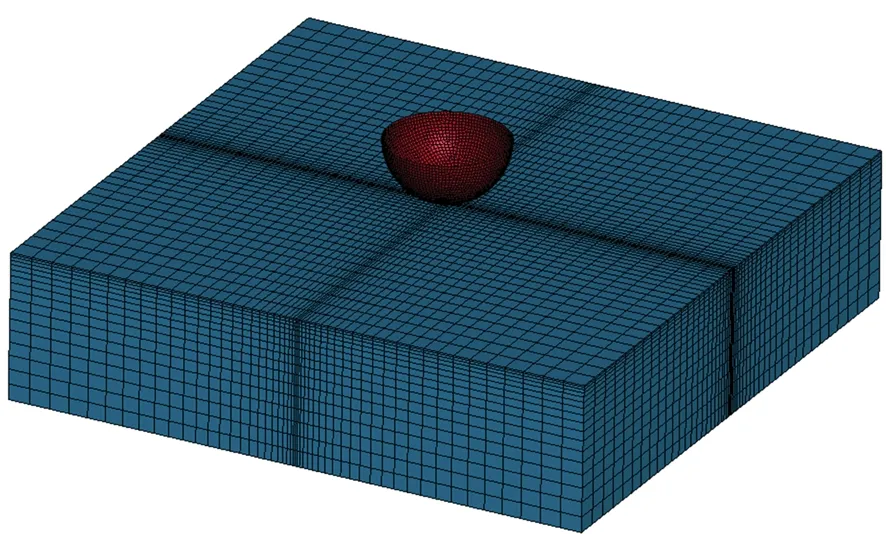
图3 土壤冲击有限元模型Fig.3 Soil impact finite element model

表1 土壤特性参数[26-27]Tab.1 Characteristics parameters of the soil[26-27]
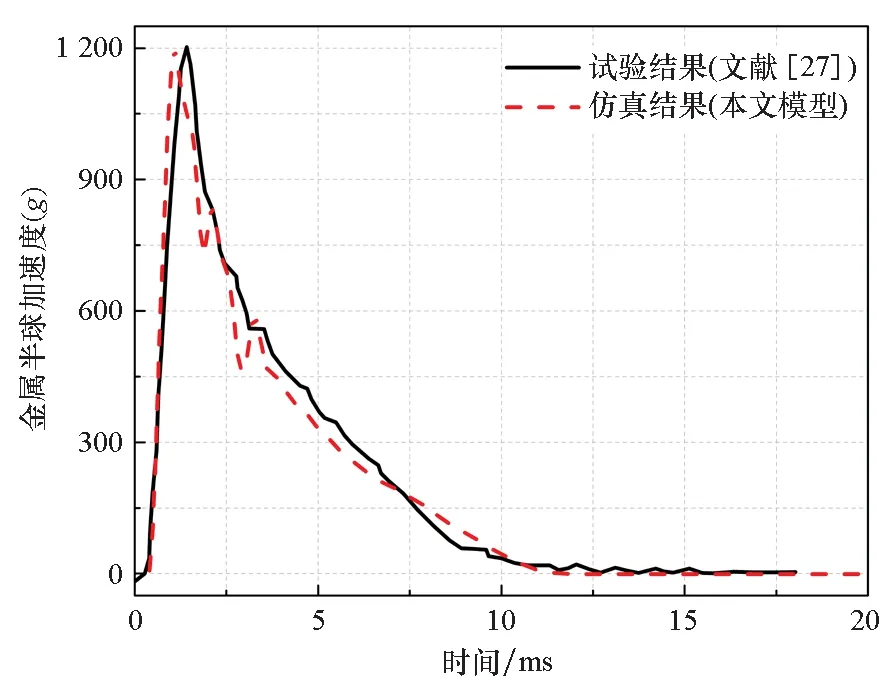
图4 土壤冲击过程的仿真与试验结果对比Fig.4 Comparison of simulation and test results of soil impact process
2 月面着陆气囊的缓冲过程分析
2.1 月面着陆气囊的设计
以“嫦娥三号”的着陆工况[28]为研究对象,对月面着陆气囊进行设计。圆柱形气囊的结构形式简单,在着陆缓冲领域应用广泛[23],月面着陆气囊同样设计为圆柱形。对于排气型气囊,基于能量守恒定律,气囊的缓冲行程与缓冲过载、速度等参数的关系可表示为[29]
(16)
式中,h0为缓冲行程,v0为气囊触月时有效载荷的初始垂直着陆速度,v1为有效载荷在气囊缓冲行程结束时的垂直着陆速度,n为最大缓冲过载,η为气囊的缓冲效率。精密电子设备允许的冲击加速度为5g~10g[30],取最小值,并考虑一定的安全系数,所以n=5×0.6=3.0g,“嫦娥三号”的名义落月速度为3.8 m/s,假设v1=0,并取η=0.4[31],则有h0=0.713 m,因此,可取圆柱形气囊的横截面直径为D0=0.8 m。
气囊系统由6个气囊组成[15],“嫦娥三号”探测器发射状态的包络尺寸为直径3.650 m、高度3.300 m[28]。对气囊母线长度进行设计时,应避免各个气囊之间发生接触,那么圆柱形气囊最大长度不能超过1.363 m,如图5所示。又考虑到圆柱形气囊充气后端面会向外鼓出,例如,横截面直径为0.8 m、母线长度为1.0 m的圆柱形气囊充气到8.0 kPa时,气囊最大长度为1.311 m[24],为保证在缓冲过程中气囊之间不相互影响,且留有一定的间隙,因此,取气囊母线长度为L0=1.0 m。

图5 圆柱形气囊母线长度的设计Fig.5 Design of axial length of the cylindrical airbag
2.2 月面气囊的动力学建模
“嫦娥三号”探测器要求可承载质量为1 242~1 350 kg[28],本文取最大值。在着陆缓冲过程中会控制探测器的水平着陆速度趋近于0[28],因此,可忽略水平速度的影响,取单个气囊进行分析,只考虑其沿竖直方向上的运动。单个气囊的承载为M=225.0 kg。基于第1节中气囊与土壤的建模方法,建立考虑月壤特性的月面着陆气囊有限元模型,如图6所示。前沿时间取0.02~0.03 s[25],月表土壤剪切波速普遍值为15~35 m/s[26],根据式(6)可求得所影响的土壤深度为0.225~0.525 m,因此建立的土壤模型尺寸为0.5 m×3.0 m×3.0 m。气囊的初始内压为P0=2.0 kPa,充入气体为空气,初始温度为T0=20 ℃,排气阈值压力为Pop=7.0 kPa,排气口直径为Dor=0.2 m。月壤的物理及力学特性参数如表2所示,其中,月壤I的参数取真实月壤普遍值的均值[26],月壤II的参数取最小值,即月壤Ⅱ比月壤Ⅰ更软。根据月壤的弹性模量可求得其体积模量,根据式(15)可求得屈服参数a0、a1、a2,计算结果如表3所示。气囊织物的材料参数、各部分的连接与接触设置均和1.1节中的相同。

图6 考虑月壤特性的月面着陆气囊有限元模型Fig.6 Finite element model of lunar landing airbag considering lunar soil properties

表2 月壤特性参数[26,32]Tab.2 Characteristics parameters of the lunar soil[26,32]

表3 月壤体积模量及屈服参数Tab.3 Bulk modulus and yield parameters of the lunar soil
月壤泡沫模型与刚体模型的计算结果对比如图7所示。从图7中可以看到,无论是以泡沫模型来考虑月壤的特性,还是将月壤假设为刚体,气囊系统的着陆缓冲过程是类似的,有效载荷均撞击了月面,这主要是因为排气口过大,气囊排气过快而导致的,所以需要进行调整。不考虑硬着陆产生的冲击,缓冲过程中三种模型的最大加速度均小于3.30g,这表明气囊尺寸的设计基本合理。
此外,从图7中还可以发现,对于月壤Ⅰ,有效载荷撞击月面之前,其缓冲过程与月壤刚体模型的完全一致,说明月壤刚度大于气囊刚度,月壤变形很小;有效载荷撞击月面后,由于月壤有一定的弹性,因而产生的冲击加速度略小于刚体模型的计算结果。0.5 s时,月壤I的变形如图8所示,下陷的最大深度为4.00 cm。对于月壤Ⅱ,其较软,缓冲过程中更快地下陷,因而导致气囊达到排气阈值压力的时间后移(如图7(a)所示),所以加速度第一个峰值的时间也随之后移(如图7(b)所示)。由于月壤下陷后气囊的接触面积变大,因此加速度的第一个峰值略有增大,使得有效载荷撞击月面时的速度变小(如图7(c)所示),加速度的第二个峰值更小(如图7(b)所示)。0.5 s时,月壤Ⅱ下陷的最大距离达到了18.75 cm。此时,气囊已完全陷入了月壤中,如图9所示。

(a) 气囊内压(a) Airbag pressure

(b) 有效载荷加速度(b) Payload acceleration
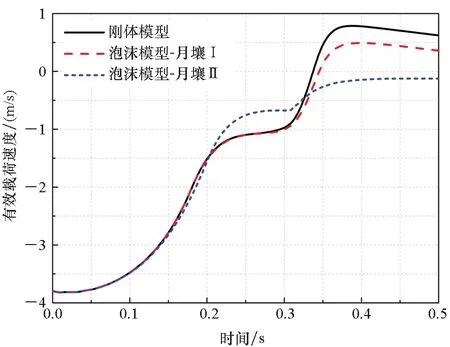
(c) 有效载荷速度(c) Payload velocity

(d) 有效载荷位移(d) Payload displacement图7 月壤刚体模型与泡沫模型的计算结果对比Fig.7 Comparison of calculation results between the rigid body model and crushable foam model of lunar soil
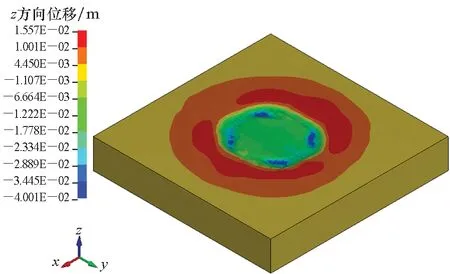
图8 月壤Ⅰ的变形Fig.8 Deformation of the lunar soil Ⅰ
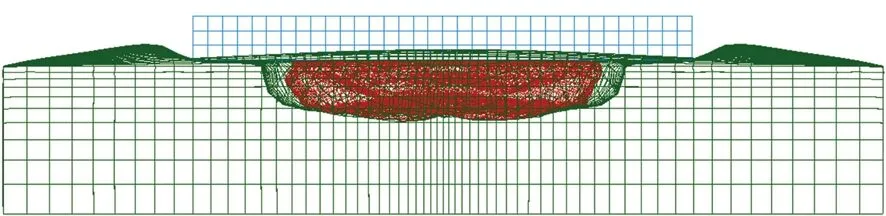
图9 气囊完全陷入月壤Ⅱ中的状态Fig.9 The state where the airbag was completely immersed in the lunar soil Ⅱ
上述结果表明,月壤参数对气囊着陆缓冲过程有较大的影响。对于该着陆工况,大部分的月壤可简化为刚体,若月壤较软则必须考虑其物理及力学特性。因此,在进行月面着陆气囊的缓冲分析时必须评估月壤的影响。
需要说明的是,在计算时假设排气口大小始终保持不变,即使气囊陷入了月壤中。
由于排气口过大,月壤参数对气囊峰值压力和有效载荷最大加速度的影响并不明显,如图7(a)和图7(b)所示。为排除排气口大小的影响,假设气囊不对外排气(排气口直径Dor=0 m),则气囊的月面着陆缓冲计算结果如图10所示。可以发现,月壤越软,缓冲过程中气囊峰值压力和有效载荷最大加速度越小,即月壤也能够起到一定的缓冲作用。

(a) 气囊内压(a) Airbag pressure

(b) 有效载荷加速度(b) Payload acceleration图10 Dor=0 m时的气囊缓冲计算结果Fig.10 Calculation results of airbag cushioning when Dor=0 m
从图10中还可以看到,相对于月壤Ⅰ,刚体模型计算得到的气囊峰值压力、有效载荷最大加速度的偏差分别为6.3%、4.8%;相对于月壤Ⅱ,其偏差分别为37.2%、31.4%。因此,对于气囊不对外排气的工况,月壤Ⅰ仍然可简化为刚体,误差较小,而月壤Ⅱ不能简化为刚体。
从本质上来说,月壤能否被压溃与其所受到的压强有关[5]。无论着陆工况如何,一旦月壤所受的压强过大,就会对气囊的着陆缓冲过程产生影响。根据计算结果,对于月壤Ⅰ,当其受到的压强小于189.7 kPa(工况Dor=0 m)时,气囊的着陆缓冲过程基本不受影响;对于月壤Ⅱ,当其受到的压强大于53.1 kPa(工况Dor=0.2 m)时,气囊的缓冲过程将受到较大的影响。所以,依据月壤所受压强,就能对其影响进行初步评估。
月壤本身也具有一定的缓冲性能,且越软缓冲效果越好,但是在选择着陆点时应避开过软的月面,因为气囊可能会陷入月壤中,不利于对外排气,影响其缓冲性能;并且月壤过软也不利于着陆物资的运输和移动。若着陆点已选定,可以通过调整气囊尺寸、充气压力、排气口大小、有效载荷质量、着陆速度等参数来降低月壤所受的压强,从而避免月壤因变形过大而影响气囊对外排气。
根据上述思想,对于“嫦娥三号”探测器,若着陆点月面为月壤Ⅰ,2.1节中的气囊结构设计是可行的(调整Dor=0.15 m,探测器能够平稳着陆)。若为月壤Ⅱ,则需要增大气囊尺寸,经计算发现,由于气囊结构尺寸的限制(如图5所示),在不降低有效载荷质量或着陆速度的情况下,难以找到合适的参数使得有效载荷最大加速度不大于5.0g,且在缓冲过程中气囊不陷入月壤中。
3 月壤参数对气囊缓冲性能的影响
气囊着陆过程中有效载荷最大冲击加速度和气囊峰值压力是评价气囊缓冲性能最重要的两个指标。前者用来评估着陆后物资是否正常可用,后者用来评估气囊织物是否会发生破裂。除此之外,气囊不应陷入月壤中。同一工况下,月壤越软,气囊下陷得越深,有效载荷的最大下落高度越大,因此可将其作为一个缓冲性能指标。且定义最大下落高度为从气囊接触月面开始到缓冲结束时有效载荷最大位移的绝对值。
描述可压溃泡沫模型的参数主要有6个:土壤密度ρ,剪切模量G,体积模量K和屈服常数a0、a1、a2。实际土壤复杂,但主要与这6个参数相关。分析这些参数对气囊缓冲性能的影响规律,就能够得到不同土壤对气囊缓冲性能的影响。根据2.2节的分析结果,为避免排气口大小的影响,下面以月壤Ⅱ、Dor=0 m的模型为基础进行分析。
3.1 影响因素分析
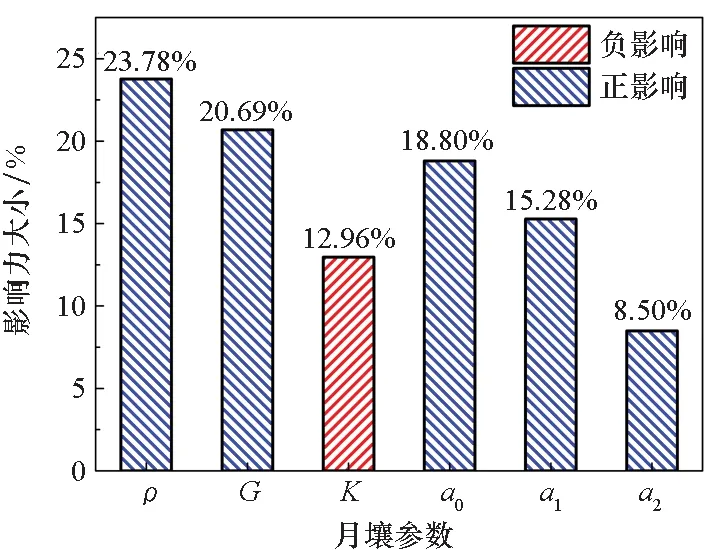
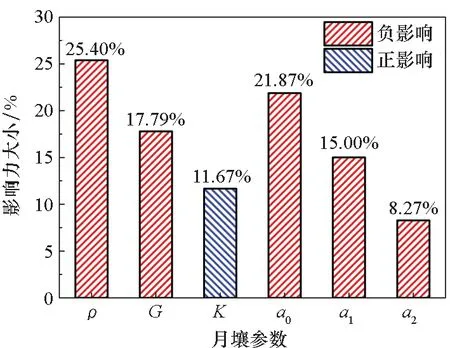
各个参数对气囊缓冲性能的影响力大小是不一样的,通过影响因素分析[33]可以得到影响月面着陆气囊缓冲性能的主要参数。首先,针对上述月壤参数设计了6因素4水平的正交试验表L32(64),各个因素的取值如表4所示。然后,对这32组试验进行仿真分析,求得缓冲过程中的气囊峰值压力(Pmax)、有效载荷最大加速度(amax)和最大下落高度(hmax)。最后对正交试验设计的结果进行极差分析[34],得到各个参数对上述3个缓冲性能指标的影响力大小如图11所示。
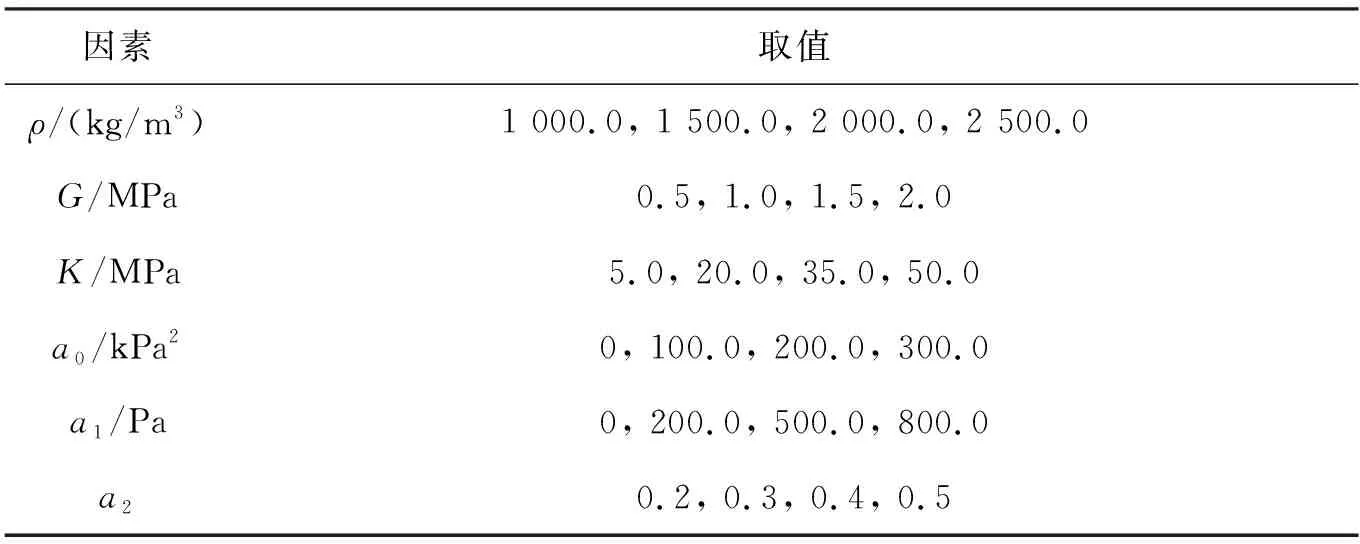
表4 正交试验设计各个因素的取值Tab.4 Value of various factors in orthogonal experiment design

(a) 气囊峰值压力(a) Airbag peak pressure
(b) 有效载荷最大加速度(b) Payload maximum acceleration
(c) 有效载荷最大下落高度(c) Payload maximum drop height图11 月壤参数对缓冲性能的影响力大小Fig.11 Influence degree of lunar soil parameters on the cushioning performance
从图11中可以看到,月壤密度ρ、剪切模量G及屈服常数a0和a1这4个参数对气囊峰值压力、有效载荷最大加速度和最大下落高度这3个缓冲性能指标的影响力大小均在15%以上,其中土壤密度ρ的影响均是最大的,超过了23%。
因此,影响气囊缓冲性能的主要参数为月壤密度ρ、剪切模量G及屈服常数a0和a1,且其对气囊峰值压力和有效载荷最大加速度为正影响,对有效载荷最大下落高度为负影响,即这4个月壤参数越大,前两个缓冲性能指标越大,后一个缓冲性能指标越小。这主要是因为这4个参数越大,月壤的刚度越大,变形越小。
3.2 影响规律研究
通过影响因素分析得到了影响气囊缓冲性能的主要影响参数,但这些参数的具体影响规律还不明晰。下面对月壤密度ρ、剪切模量G及屈服常数a0和a1这4个参数分别进行研究。
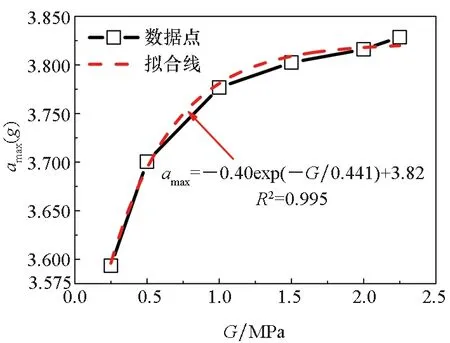
气囊峰值压力、有效载荷最大加速度和最大下落高度随上述4个参数的变化曲线如图12~15所示。可以看到,前两个缓冲性能指标随着这些参数的增大而增大,后一个性能指标随着这些参数的增大而减小,这与影响因素分析的结果是一致的;并且,随着月壤参数的增大,3个缓冲性能指标均逐渐趋于一个定值,这是因为月壤越硬,对缓冲性能的影响越小。

(a) 气囊峰值压力(a) Airbag peak pressure

(b) 有效载荷最大加速度(b) Payload maximum acceleration

(c) 有效载荷最大下落高度(c) Payload maximum drop height图12 月壤密度ρ对着陆气囊缓冲性能的影响Fig.12 Influence of lunar soil density ρ on the cushioning performance

(a) 气囊峰值压力(a) Airbag peak pressure
(b) 有效载荷最大加速度(b) Payload maximum acceleration
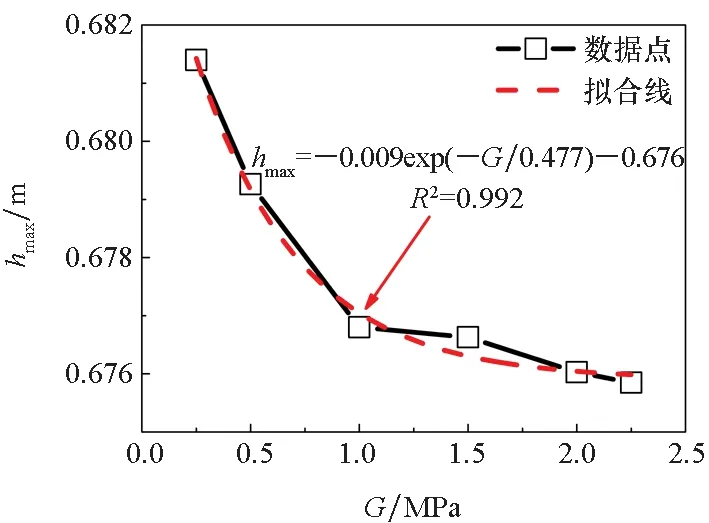
(c) 有效载荷最大下落高度(c) Payload maximum drop height图13 剪切模量G对着陆气囊缓冲性能的影响Fig.13 Influence of shear modulus G on the cushioning performance
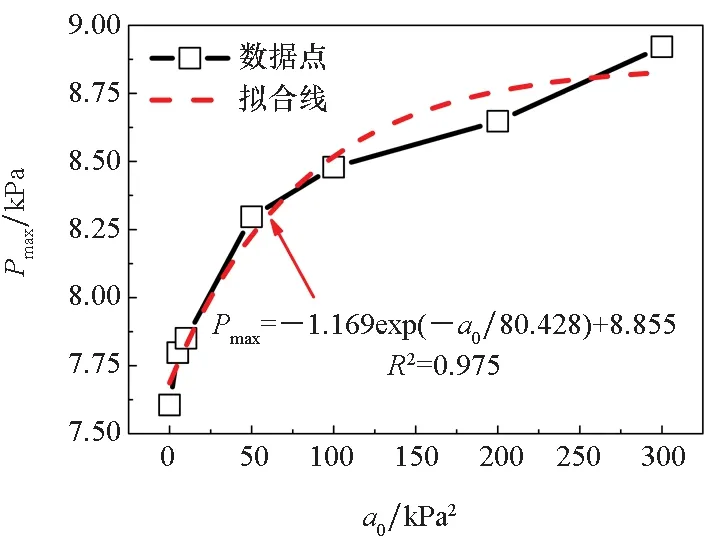
(a) 气囊峰值压力(a) Airbag peak pressure

(b) 有效载荷最大加速度(b) Payload maximum acceleration

(c) 有效载荷最大下落高度(c) Payload maximum drop height图14 屈服参数a0对着陆气囊缓冲性能的影响Fig.14 Influence of yield parameter a0 on the cushioning performance
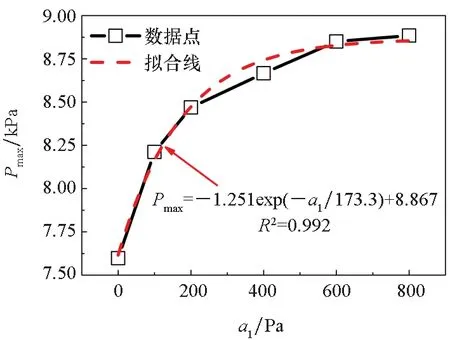
(a) 气囊峰值压力(a) Airbag peak pressure
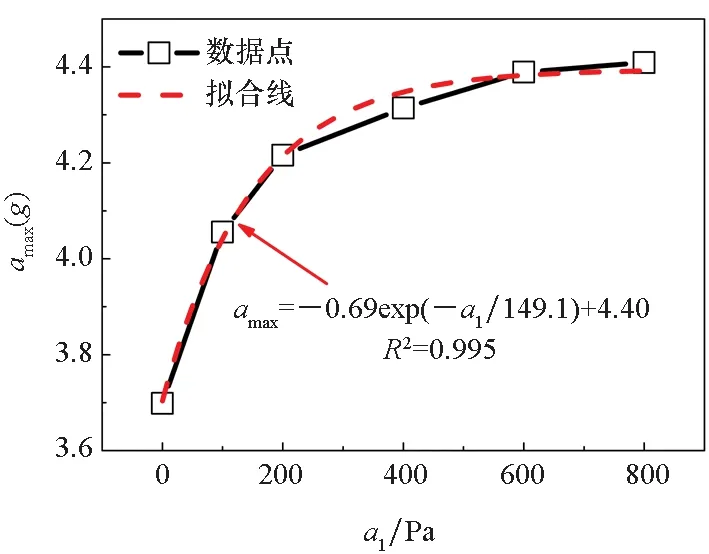
(b) 有效载荷最大加速度(b) Payload maximum acceleration

(c) 有效载荷最大下落高度(c) Payload maximum drop height图15 屈服参数a1对着陆气囊缓冲性能的影响Fig.15 Influence of yield parameter a1 on the cushioning performance
对这些数据点进行拟合,可以发现,上述4个月壤参数与3个缓冲性能指标之间均满足指数函数关系,即
y=A1exp(-x/t1)+y0
(17)
式中,x月土壤参数,y为缓冲性能指标,A1、t1和y0均为拟合系数。
4 结论
气囊装置对于月面物资的着陆缓冲具有显著优势,在进行月面着陆缓冲分析时,必须考虑月壤的影响。本文根据“嫦娥三号”的着陆工况设计了圆柱形的月面着陆气囊,建立了考虑月壤特性的气囊缓冲动力学模型,并采用该模型研究了月壤对气囊缓冲性能的影响,得到了月壤参数的影响规律,主要结论如下:
1)虽然月壤也能够起到一定的缓冲作用,但是从可靠性的角度来看,在选择着陆点时应考虑对气囊缓冲性能影响小的月壤,因为月壤较软时,气囊可能会陷入月壤中,不利于对外排气,进而影响其缓冲性能。
2)通过对比缓冲过程中气囊峰值压力、有效载荷最大加速度和最大下落高度这3个性能指标能够确定合适的月壤,并且月壤密度、剪切模量及屈服参数a0和a1这4个参数对上述3个指标的影响较大,因此选择着陆点时需重点考察。
3)气囊峰值压力和有效载荷最大加速度随上述4个月壤参数的增大而增大,而有效载荷最大下落高度随之减小,但均逐渐趋于一个定值。并且,这4个月壤参数与缓冲性能指标之间都满足指数函数关系,基于该关系就能够得到月壤参数变化时缓冲性能的具体变化。
