多旋翼无人机模型预测抗扰避障制导
2022-08-06兰庆湘雍可南
兰庆湘,陈 谋,雍可南
(南京航空航天大学 自动化学院, 江苏 南京 211100)
多旋翼无人机因其机动性强、易于操作等优点广泛应用于军用和民用领域中,如侦察作战、通信传输、航拍摄影和巡线检修等。但随着应用场景不断扩大和更新,多旋翼无人机发生碰撞造成的坠机事故也不断增加。因此,多旋翼无人机需要具备自主避障的功能,这是完成复杂任务的前提[1-4]。针对无人机、无人车等无人系统的避障问题,常见的避障方法有人工势场法[5-7]、基于神经网络和强化学习等的智能算法[8-10]、基于模型预测控制的方法[11-13]等。具体而言,人工势场法通过设置目标的吸引力和障碍物的排斥力使得无人机在搜索路径时沿着负梯度方向以寻找合适的避障路径[5]。这一方法在实际应用中易于实现,但可能出现梯度为零的情况导致陷入局部极小值点。文献[6]通过增加了转向力和恢复力来避免陷入局部极小值点。文献[7]基于自触发控制与人工势场法,采用了机器人操作系统(robot operating system, ROS)与运动捕捉相机实现了室内环境下的无人机避障。随着人工智能的迅速发展,许多研究人员将神经网络和强化学习等智能算法应用于无人机避障的研究中。文献[8]基于深度学习在四旋翼上采用了能够测量像素的亮度变化来输出信号的事件相机,并实现了动态障碍物的避障。文献[9]通过强化学习对碰撞概率进行估计,使得无人机在未知场景中保持低速,减少了碰撞可能。文献[10]采用案例的推理算法实现了对已知类型障碍物的避障,对未知类型的障碍物采用改进的人工势场法避障而后保留在案例库中,并在实际移动机器人平台上验证了该算法的可行性。然而,存在外部干扰的情况下不依赖外部环境已知信息的无人机避障问题还需进一步研究。
模型预测控制(model predictive control, MPC)广泛应用于无人机避障方面,国内外许多学者进行了基于MPC的无人机避障方法研究。文献[11]针对无人车的避障问题,基于三维危险势场进行路径规划,采用了多约束模型预测控制实现路径跟踪,仿真结果表明了该方法良好的避障与跟踪性能。文献[12]针对无人机的动态避障问题设计了轨迹分类方案,将动态障碍物的预测轨迹引入MPC的避障约束条件,采用室内运动捕捉系统获取无人机和障碍物的数据,通过远程计算机向小型四旋翼Crazyflie发送指令实现了室内的无人机避障。文献[13]提出的轨迹生成框架将具有不确定性的障碍物未来轨迹表述为具有置信度的碰撞区域,在MPC中构造概率约束,仿真结果表明了该方法能够比没有预测的方法更好地实现避障。文献[14]考虑了自主水下机器人传感器探测距离较短的问题,将路径规划问题转化为滚动时域优化问题,构造误差动力学并采用MPC实现了路径规划与跟踪控制一体化,并通过实际的水下航行器动力学模型验证了所提算法的有效性。显然,前述基于模型预测的方法能够实现避障的目标。但是,多旋翼无人机在执行任务时容易受到风等外部干扰,因此对所设计的制导律需要具有一定的抗干扰能力。
干扰观测器(disturbance observer, DOB)通过根据系统的实际输入与输出得到干扰估计值,将其作为补偿从而消除干扰对系统性能的影响,这种方法可以和不同的制导策略结合,且易于实现,在许多领域被广泛应用[15-17]。文献[18]针对MPC的抗干扰问题将非线性干扰观测器和MPC结合起来,构造了复合飞行控制器,通过仿真验证了干扰条件下的算法效果。文献[19]设计了不同的干扰观测器对未知干扰和已知谐波频率的干扰进行估计,与MPC结合实现了对轮式机器人的轨迹跟踪,并通过仿真与实验验证了该方法的有效性。文献[20]针对机电一体化系统的控制,将干扰观测器的补偿信号融入MPC解算最优轨迹中,通过实验验证了所提出的基于干扰观测器的MPC比传统的MPC更加有效。上述文献通过干扰观测器对MPC进行补偿,或将干扰观测器的估计值融入MPC的优化求解过程中,实现了较好的效果,但基于MPC的多旋翼无人机抗扰避障方法还需进一步研究。
多旋翼无人机在执行任务时,将通过机载传感器感知外部环境,实时传递感知到的障碍物信息至制导与控制系统,并运行避障制导律获取避障制导指令,通过控制系统对制导指令跟踪实现障碍避让,保证轨迹跟踪过程的飞行安全。基于上述研究背景,本文针对多旋翼无人机避障与轨迹跟踪问题,通过综合设计干扰观测器、辅助制导律和MPC算法,提出了一种抗扰避障制导律设计方法,并进行数值仿真与实物飞行验证。
1 问题描述
鉴于多数情况下多旋翼无人机将搭载单线激光雷达,其可感知的障碍物将以二维平面为主,同时考虑到维数增加带来的优化求解速度降低问题,因此只考虑二维平面,即多旋翼无人机水平方向的运动实现避障。水平方向下多旋翼无人机的状态量(二维位置和偏航角)p=[x,y,ψ]T与输入量(机体速度和偏航角速率)v=[u,v,r]T的关系可通过运动学方程获得。考虑到实际飞行中存在的干扰,多旋翼无人机水平方向的运动方程[21]为:
(1)
式中,干扰为vid=[uid,vid,rid]T。
为了便于表述,令转换矩阵为:
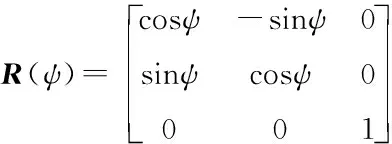
(2)
则式(1)可简写为:
(3)
备注1干扰vid并不与实际干扰具有一一对应关系,而是无人机系统在机体坐标系下的等效干扰,可能包括但不限于风干扰、传感器漂移等。
考虑到实际多旋翼无人机的速度有限,在设计制导律时需要对输入添加以下限制条件:
(4)
其中,vmax为一正常数。
鉴于是在跟踪背景下研究多旋翼无人机的避障,定义参考轨迹pr=[xr(t),yr(t),ψr(t)]T由如下系统产生:
(5)
式中,vr=[ur,vr,rr]T为参考速度与偏航角速率。

定义第i个障碍物坐标为poi=[xoi,yoi]T(i=1,2,…,No),障碍区域的威胁半径为roi。其中障碍物坐标位置可能与参考轨迹的距离小于障碍区域的威胁半径,如图1所示。

图1 障碍物与参考轨迹示意Fig.1 Schematic diagram of obstacles and reference trajectory
目标为:针对多旋翼无人机水平方向运动模型式(3),设计避障制导律,在满足输入饱和约束式(4)与避让图1所示障碍物的前提下,使得多旋翼无人机跟踪由式(5)生成的参考轨迹。
为了方便制导律设计和稳定性分析,需对外部干扰进行假设,具体如下:

2 基于模型预测的避障制导律设计
本节首先设计干扰观测器来估计未知干扰,然后设计辅助制导律作为MPC的约束参考量,最后给出基于模型预测的避障制导律设计方法并分析整个闭环系统的稳定性。
2.1 干扰观测器设计
为了估计未知干扰,定义z为设计的观测器内部状态,构造如式(6)所示的干扰观测器[22]。
(6)

(7)
定义干扰估计误差为:
(8)
结合式(6)与假设1,对式(8)求导得:

=-S(p)R(ψ)evid
(9)
为了保证S(p)R(ψ)为正定矩阵,构造T(p):
(10)
其中,kd1>0,kd2>0用于调节干扰观测器增益。
由式(7)可得:
(11)
其中,η1和η2的取值为η1=-xsinψ+ycosψ,η2=-xcosψ-ysinψ。
从而得到增益矩阵S(p)R(ψ):
(12)
2.2 辅助制导律设计
本小节通过设计辅助制导律来构造李雅普诺夫约束条件,以保证闭环系统在所设计的基于模型预测的抗扰避障制导律下的稳定性。
构造误差:
(13)
多旋翼无人机与第i个障碍物的距离为:
(14)
参考文献[23],构造多旋翼无人机与第i个障碍物的势能函数:
(15)
式中,参数R>0。
式(15)对x和y的偏导数分别为:
(16)
(17)
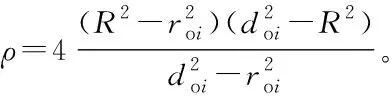
多旋翼无人机与障碍物的整体势函数为:
(18)
式中,ko>0用于调节避障成本与状态成本的权重。
构造如下变量:
(19)
(20)
(21)
其中,km1和km2为大于零的可调参数。
采用的制导律为:
(22)
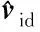
(23)
其中,kl为可调参数。
针对上述设计的辅助制导律,为便于后文的结论分析,归纳其特征于定理1。
定理1考虑式(3)所示的具有外部有界干扰的多旋翼无人机运动学方程,采用式(22)所示的制导律,当选取参数KM=diag(km1,km2,km3),KN=diag(kn1,kn2,kn3)满足式(24)~(25),则可以使闭环系统的误差最终一致有界,且同时实现避障与跟踪的目标。
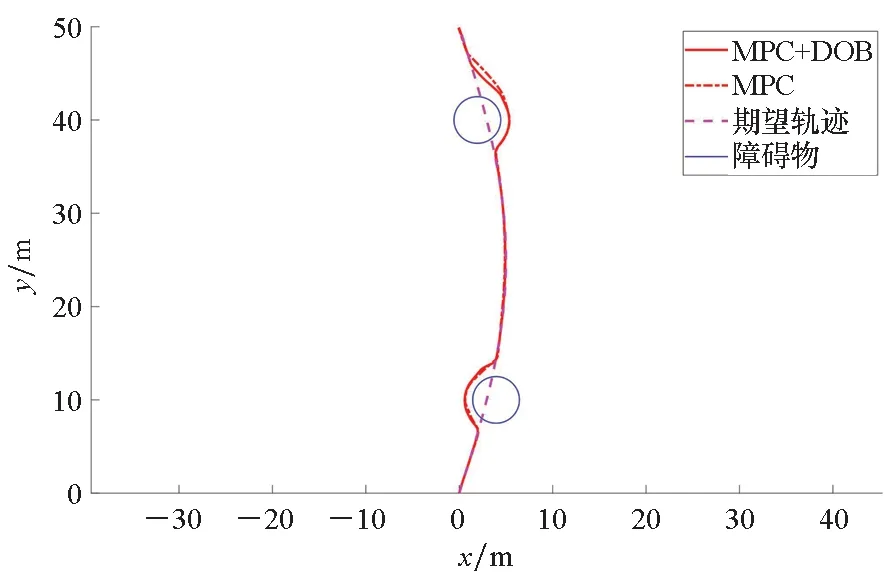
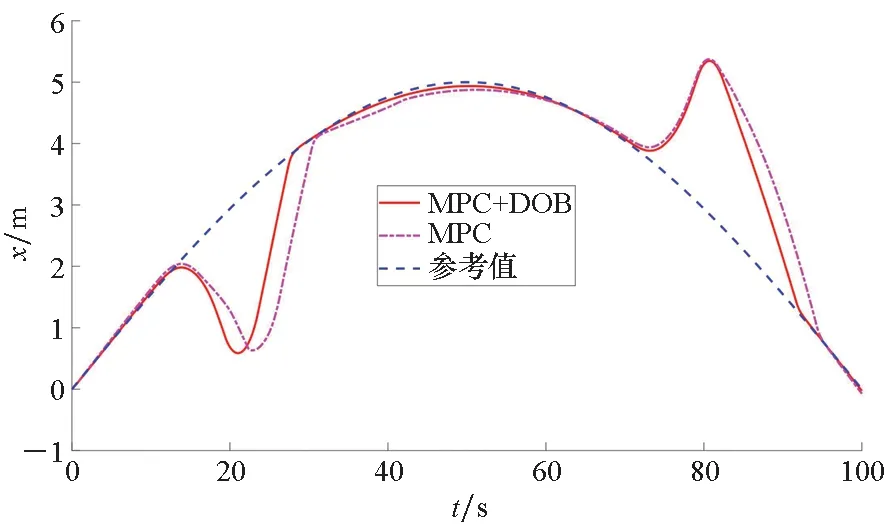
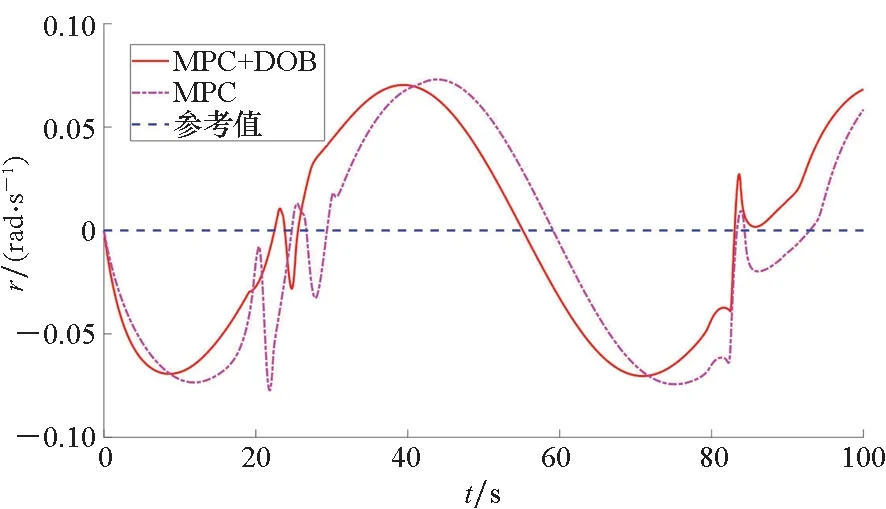
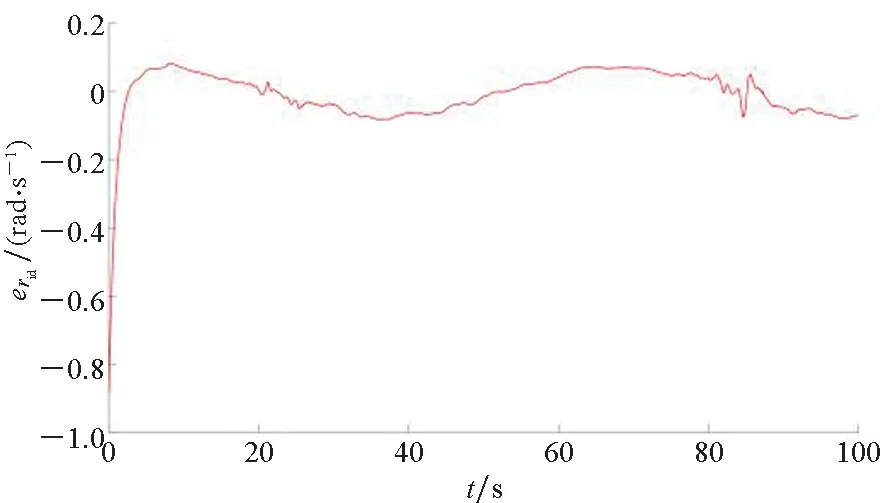
0 (24) (25) 证明:考虑如下所示的李雅普诺夫函数: V=V1+V2+Vo (26) 对式(26)求导,得到V的导数为: (27) 考虑式(3)、式(8)、式(9)、式(13)、式(21)、式(22),则式(27)可以写成如下形式: koζTR(ψ)va1+koζTR(ψ)evid (28) (29) 将式(23)代入式(29)抵消掉后三项,从而得到: (31) 为了进一步改善避障与跟踪效果,基于MPC结合上述辅助制导律进行设计。 给定MPC的预测周期为T,预测步长为N,采样周期为δ,则有T=Nδ。 对于每一个预测时刻,成本函数为: (32) tk时刻预测的N个步长的成本函数累加得到总成本函数: (33) 根据式(27)得到的李雅普诺夫函数导数,添加如式(34)所示的稳定性约束条件[24]。 (34) 采用式(33)的成本函数,添加式(4)和式(34)所示的约束条件,MPC优化问题为: (35) 基于模型预测的抗扰避障制导算法的主要步骤如下所示。 步骤1:选取合适的采样间隔δ、多旋翼无人机状态初值以及参数设置,给出参考状态与参考输入、障碍物坐标与半径,初始仿真步数k=0,初始仿真时间tk=0,选取最大仿真时间tmax; 步骤3:求解优化问题(35)得到制导指令v(tk); 步骤4:求解得到的tk时刻的解v(tk)作为当前仿真步长,即[tk,tk+δ]时间内的输入,根据式(3)更新多旋翼无人机的状态值; 步骤5:tk=tk+δ,k=k+1,重复步骤2~5至tk≥tmax。 针对上述算法中设计的避障制导律,可以得到如下定理: 定理2考虑式(3)所示的具有外部有界干扰的多旋翼无人机运动学方程,采用优化问题式(35)求解得到的制导律,当初始时刻t0有解时,则对于任意时刻MPC优化问题能够保证有解,在所设计的制导律下多旋翼无人机能够实现避障与轨迹跟踪。 (36) 故式(22)所得到的va有界。 (37) 由va有界可知式(37)所示的输入序列符合约束式(4)。因此由数学归纳法可知当t0时刻存在解时,能够保证优化问题式(35)的递归可行性。又由式(34)可知对于任意tk时刻 (38) 即在优化问题式(35)求解得到的制导律下能够实现轨迹跟踪与避障。 备注2避障与跟踪的效果可以通过相关参数进行调节。当多旋翼无人机系统状态与输入的成本权重Q和R选取过大时,会导致多旋翼无人机过多偏向于参考轨迹,进而导致避障失败;反之,当避障成本权重ko选取过大时,会使多旋翼无人机更加远离障碍物,导致跟踪效果变差,甚至任务失败。因此,用户在进行权值设置时,需要结合实际情况进行适当取舍。另外,当多旋翼无人机系统的速度限幅区间较大时,多旋翼无人机会采取更加剧烈的机动过程实现避障。然而,受制于姿态回路的响应,过于剧烈的机动过程会导致多旋翼无人机的估计产生较大的波动,甚至控制失效;另一方面,当限制较小时,避障过程将耗费更久时间,且完成避障后对参考轨迹的跟踪也更慢。因此,在实际飞行测试中需要多次测试选取合适的参数取值。采样周期δ与实际飞行测试中程序的运行周期有关,因此选择与飞控程序运行周期相近的值。预测步长N较小则会使避障与跟踪效果变差,但N增大会增加每个周期的解算时间,过大可能会导致无法在指定的周期完成实时解算,因此需要在能保证实时性的前提下选择较大的步长。 为验证所提出的避障方法的有效性,基于文献[25]提出的开源求解器Casadi编写C++程序进行数值仿真与实际飞行验证。 值得注意的是,式(23)中分母可能存在为零的时刻,即Excosψ+Eysinψ=0或-Exsinψ+Eycosψ=0。这种情况下表示误差在机体系下的投影量(障碍物不在区域内)或误差与势能的叠加在机体系下的投影量(障碍物在检测区域内)为零。为了避免使多旋翼无人机陷入这一局部极值点,应添加常量使多旋翼无人机跳出该点继续前进。考虑到实际中取等号的情况较严苛,当|Excosψ+Eysinψ|≤时令ua1取值为ua1=时令va1取值为 期望轨迹为: (39) 期望速度ur,vr与偏航角速率rr由式(40)给出。 (40) 干扰量设为: (41) 考虑到多旋翼无人机实际的飞行速度的大小与变化律,式(41)所设置的干扰量的变化速度远慢于飞机速度变化,所以可以认为满足假设1。 选取仿真时长tmax=100 s,障碍物坐标为[3.93,10]T和[1.93,40]T,障碍物的威胁半径ro1=ro2=1.5 m。选取干扰观测器参数kd1=kd2=1,辅助制导律参数KM=diag(1,1,1),KN=diag(2,2,2),kl=1,避障成本参数ko=1。MPC采样间隔δ=0.02 s,预测步长N=10。考虑到实际飞行中的不确定性,所设置的成本权重参数R中关于速度的两项较小,即不一定要严格按照期望的速度飞行。因此,权重矩阵Q=diag(5,5,10),R=diag(0.5,0.5,10)。 为了尽可能在飞行过程中确保飞行的安全,偏航角速率尽可能变动较小,多旋翼无人机的速度也应限制在合理的安全范围内。因此,将速度与偏航角速度约束设为: (42) 使用上述参数进行仿真,多旋翼无人机的初始状态为p0=[0,0,0]T,多旋翼无人机初始设为悬停状态,干扰观测器的内部状态初值设为z=[2,2,2]T。 为了体现方法在抗扰避障过程中的效果,本节给出常规MPC算法的仿真,并与本文所提出的方法进行比较,仿真结果如图2~5所示。从图2可以看出,受外部扰动的影响,常规MPC算法在规避障碍物后未能及时追踪参考轨迹,而本文所提出的抗扰避障制导律能够保证多旋翼无人机有效地避开障碍物,并在外部扰动下对期望轨迹进行较好的跟踪。图3为多旋翼无人机的二维坐标和偏航角的具体信息。相较于MPC算法,本文所提出的方法能够在接近障碍物时及时调整多旋翼无人机的状态进行规避,并在完成规避后及时跟踪参考轨迹。由于仿真中添加了外部干扰,且在跟踪与避障过程中需要结合整个系统的成本值对偏航角进行调整以获取最优的成本值,所以偏航角并不会保持固定的期望值。图4为两种方法求解的线速度与偏航角速度指令,受干扰的影响,MPC算法在规避障碍物后未能及时跟踪参考轨迹,使得跟踪误差增大,相较于本文的方法出现了较多的饱和,使得输入成本较高。由于在仿真中需要进行避障与减小干扰对多旋翼无人机的影响,而期望状态的计算中不包括这两者,所以实际求解的线速度与偏航角速度指令具有一定的偏差。从图5可以看出,随着仿真的进行,干扰观测器的估计误差逐渐减小,能够对干扰进行较好的估计。从上述仿真结果可以看出,相较于MPC算法,本文所提出的方法能够减小干扰对多旋翼无人机的影响,达到更好的避障与轨迹跟踪效果。 图2 避障仿真效果Fig.2 Obstacle avoidance simulation renderings (a) x (b) y (c) ψ图3 多旋翼无人机仿真状态Fig.3 Simulation states of multi-rotor UAV (a) u (b) v (c) r图4 MPC求解制导指令与参考值Fig.4 MPC solves guidance command and reference values (a) uid (b) vid (c) rid图5 干扰值与估计值Fig.5 Actual and estimated disturbance values 基于大疆的M600 Pro型号无人机进行实际多旋翼无人机上的算法测试与验证。考虑到多旋翼无人机自身的硬件性能有限,难以完成优化问题的实时求解,机载计算机上基于DJI所提供的开源ROS开发框架[26]编写基于ROS和C++的程序以实现所需的制导算法。 在实际飞行测试中采用本文所提出的抗扰避障制导律,结合无人机飞控所提供的控制算法完成避障。将编写的MPC程序移植在机载计算机上,采用相关ROS服务改变MPC的输入输出接口,并添加实物飞行测试中所必需的相关代码。通过自行编写的MPC程序在机载计算机上实时求解制导指令而后采用串口发送至底层飞控,从而实现多旋翼无人机避障与轨迹跟踪。障碍物由相机获得,实验过程中默认已知。 备注2中,障碍物的信息包括:其在惯性坐标系下的坐标及对应的危险半径。需要说明的是,该种障碍物信息描述方式具有通用性,当机载激光雷达或深度相机检测到障碍物后,可依据扇面信息将障碍物描述为上述形式,具体可参考文献[27]。 实际飞行验证的算法步骤如下所示。 步骤1:开启相关ROS服务以建立起飞降落请求、获取状态信息与向无人机发送制导指令的接口,完成各参数的初始化,正常运行后自动起飞至MPC程序的起点,按照设定的频率进行求解; 步骤2:获取当前时刻无人机的位置、速度以及与障碍物的距离等信息,更新干扰估计值,将获取的实时数据作为MPC的输入进行求解,得到当前时刻的制导指令; 步骤3:将求解的制导指令发送至无人机底层飞控,使无人机继续沿期望轨迹飞行或避开障碍物; 步骤4:根据ROS话题消息记录当前时刻的无人机数据以便后续分析; 步骤5:完成当前时刻的计算,更新时间tk=tk+δ,k=k+1后再从步骤2开始计算,直至tk≥tmax。 实际飞行验证中采用与仿真一致的参数设定,实验结果如图6~9所示。 图6 避障实际效果Fig.6 Obstacle avoidance actual renderings (a) x (b) y (c) ψ图7 多旋翼无人机实验状态Fig.7 Experimental states of multi-rotor UAV 图6和图7表明了本文所提出的避障制导律的实际测试效果,在远离障碍物时能够对期望轨迹进行跟踪,在接近障碍物时调整状态实现避障,并在避障完成后继续跟踪期望轨迹。相较于图2和图3其性能有所下降,这主要是仿真与实际飞行测试的差异所导致的。从图8中可以看出,MPC解算得到的制导指令发送至底层飞控后需要一定的时间才能响应,因此会对实际飞行的效果产生一定的影响。由于除了人为设定的干扰量,实际环境中必然还存在其他未知的干扰以及传感器在测量中存在的噪声,因此图9所示的干扰估计误差存在一定的波动。从实际飞行测试的结果中可以看出,本文所提出的抗扰避障制导律能够应用于实际多旋翼无人机上的轨迹跟踪与避障。 (a) u (b) v (c) r图8 无人机对算法指令的响应效果Fig.8 Response effect of UAV to algorithm command (a) euid (b) evid (c) erid图9 干扰估计误差Fig.9 Disturbance estimation error 从上述仿真和实验结果中可以看出,实验结果比仿真结果差,这是实际飞行中的实验设备、实验环境等因素导致的,主要有以下几点: 1)实际飞行中传感器的噪声对获取的多旋翼无人机状态数据存在影响; 2)多旋翼无人机的实际速度和角速度由底层的姿态回路对MPC解算的制导指令进行响应来实现,其响应特性影响着实际飞行的结果; 3)电机也具有内部动态,无法很好跟踪姿态控制器生成的参考指令,必然会对实际飞行效果产生影响。 针对上述可能产生影响的情况,可以通过调整多旋翼无人机飞行环境和自身的飞控参数等来改善实际飞行的效果。 针对干扰下的多旋翼无人机的避障问题,本文引入干扰观测器与辅助制导律,基于MPC方法设计抗扰避障制导律。数值仿真和实物飞行验证结果表明,所提出的抗扰避障制导律能够有效地规避飞行途径中的障碍物,并具有一定的抗扰能力,能够应用于小型多旋翼无人机在实际环境中实现干扰下的实时轨迹跟踪与避障。
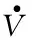
2.3 抗扰避障制导律设计


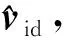

3 实验结果
3.1 数值仿真






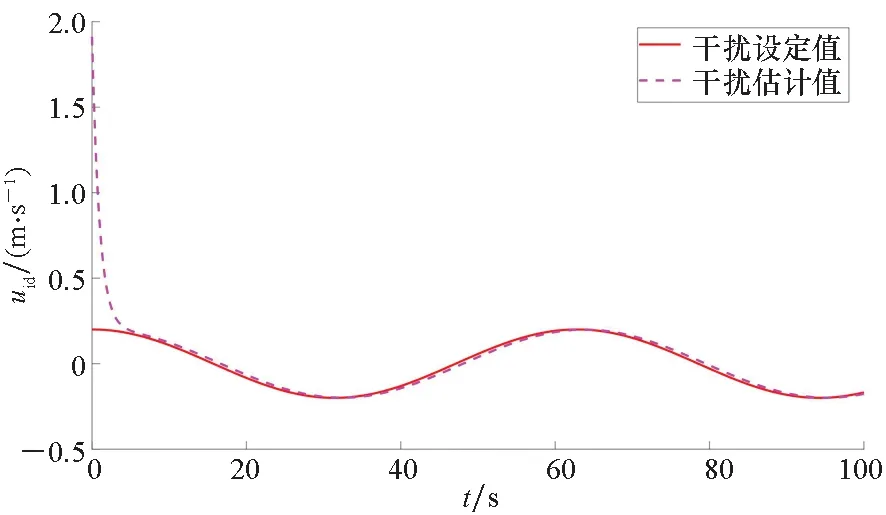
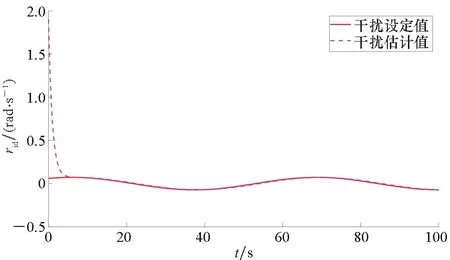
3.2 实物验证







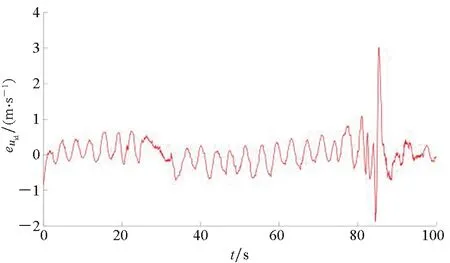
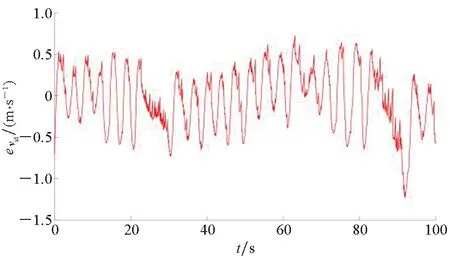
3.3 仿真与实验结果差异分析
4 结论
