旋压机液压伺服系统位置压力复合控制研究

刘 浩，赵春江,2，宁圆盛,3，边 强，王 蕊，龙 涛

(1.太原科技大学 机械工程学院，山西 太原 030024；2.山西电子科技学院 智能装备学院，山西 临汾 041000；3.燕山大学 机械工程学院，河北 秦皇岛 066004)

引言

旋压机作为一种金属塑性成型机器，其作业过程的控制精度对钢管壁厚的影响起着至关重要的作用[1-3]。旋压机液压控制系统主要通过阀控非对称液压缸进行控制，其通常采用位置闭环系统控制液压缸来实现旋轮压下量的调节。实际工作时由于负载、扰动的存在，系统压力产生波动，影响液压缸压下位置的准确性，造成大直径钢管旋压过程中出现开裂或压断的现象。因此，如何提高大直径薄壁管位置控制精度显得至关重要。

为提高压力机压力控制精度，张传锦等[4]设计了一种位置/压力自动补偿的控制系统；韩贺勇等[5]针对电液控制系统提出一种位置压力非线性自适应双闭环控制系统；WANG J等[6]在滚切剪液压伺服系统中使用位置-压力主从控制的方式提高系统的精度和稳定性；HAN H等[7]研究位置-压力主从控制方式可以提高十一辊矫直机控制系统的位置控制精度；刘亚会等[8]为解决卷曲机助卷辊压力波动大的问题，对位置压力控制环的控制参数进行了研究。以上研究表明，为了不断提高系统控制精度，位置-压力复合控制已在许多设备中得到了应用。

本研究针对大直径薄壁管旋压机液压系统提出的复合系统控制框图如图1所示。液压缸两腔的压力经压力传感器、压力-位置转换模块后与给定值进行比较，同时位移传感器的输出作用于系统的输入端，图1中压力控制回路完全被位置控制回路包围，不仅实现了主从控制，并且旋压过程中液压缸两腔压力保持稳定。

图1 旋压机位置-压力复合控制原理图Fig.1 Schematic diagram of position-pressure compound control of spinning machine

1 数学模型

电液伺服阀控制非对称液压缸原理如图2所示，A1，p1为液压缸无杆腔工作面积、压力，A2，p2液压缸有杆腔有效面积、压力。

图2 电液伺服阀控制液压缸原理图Fig.2 Principle diagram of hydraulic cylinder controlled by electro-hydraulic servo valve

1) 系统基本方程

阀的线性压力-流量方程为[9-12]：

ΔqL=KqΔxv-KcΔpL

(1)

负载流量方程为：

(2)

液压缸输出的旋压力与负载力、惯性力、黏性力等平衡[13-15]，方程为：

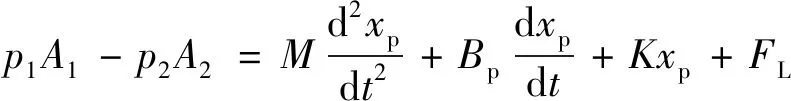
(3)

式中,Kq——阀的流量增益

Kc——阀的流量-压力系数

xv——阀芯位移

Ctp——液压缸总泄漏系数

xp——液压缸活塞位移

Ap——液压缸负载等效面积，Ap=(A1+A2)/2

M——活塞及负载的总质量

Bp——活塞和负载的黏性阻尼系数

K——负载弹簧刚度

FL——作用在活塞上的外负载力

2) 液压缸的传递函数

根据以上推导，将式(1)～式(3)进行拉普拉斯变换，得：

qL=Kqxv-KcpL

(4)

(5)

AppL=Ms2xp+Bpsxp+Kxp+FL

(6)

对式(4)～式(6)进行整理，伺服阀控制非对称液压缸的传递函数为：

(7)

其中,Kce为总流量-压力系数，Kce=Kc+Ctp。

3) 负载扰动对控制精度的影响

钢管出口厚度h为：

h=S0-(xp-S)

(8)

式中，S0——钢管预设厚度

S——旋压机弹跳值

(9)

式中，F——旋压力

Km——旋压机刚度系数

当来料管材厚度有变化时，必然会引起旋压力以及旋后钢管厚度的变化。当旋压力由F1变为F2时，则旋后钢管厚度偏差为：

(10)

在得到F2时，通过调节液压缸的流量来对旋轮位置进行修正，修正量为Δx：

(11)

式中，C——位置补偿系数，一般为0～0.8。

修正后的，出口厚度偏差为：

(12)

通过上述方式来减小负载扰动对系统控制精度的影响。

4) 各反馈回路的灵敏度

假设系统在t，(t+Δt)时刻所受的负载力FL为常数，根据式(3)可知，力平衡方程式为：

(13)

式中，xt，xt+Δt——液压缸在t，(t+Δt)时刻的位置信号

pt，pt+Δt——液压缸在t，(t+Δt)时刻的压力信号

整理式(13)得：

(14)

实际旋压过程中，Δt时间内加速度a、速度v的变化非常小，式(14)近似处理，得：

(15)

式中，Kt——液压缸输出信号经压力传感器、转换模块环节后的增益；

该环节对应的传递函数为：

可得转换控制模块的计算公式为：

x′=Kt(p′-pt)

(16)

式中，x′——转换过程的位移

p′——期望压力值

pt——t时刻的压力信号

图(1)中位移传感器将活塞杆运动的距离线性转换为电压信号，则传递函数为：

(17)

式中，Uf——位移传感器输出电压

Kf——位移传感器的灵敏度

根据旋压机液压伺服系统的组成、控制方式，可得系统传递函数方框图如图3所示。其中，Ur为输入信号；xp为活塞杆位移信号；U0为给定电压。

由方框图3可知，负载扰动相同情况下，复合控制时，液压系统的实际输出与设定值的偏差比位置控制时的偏差小。

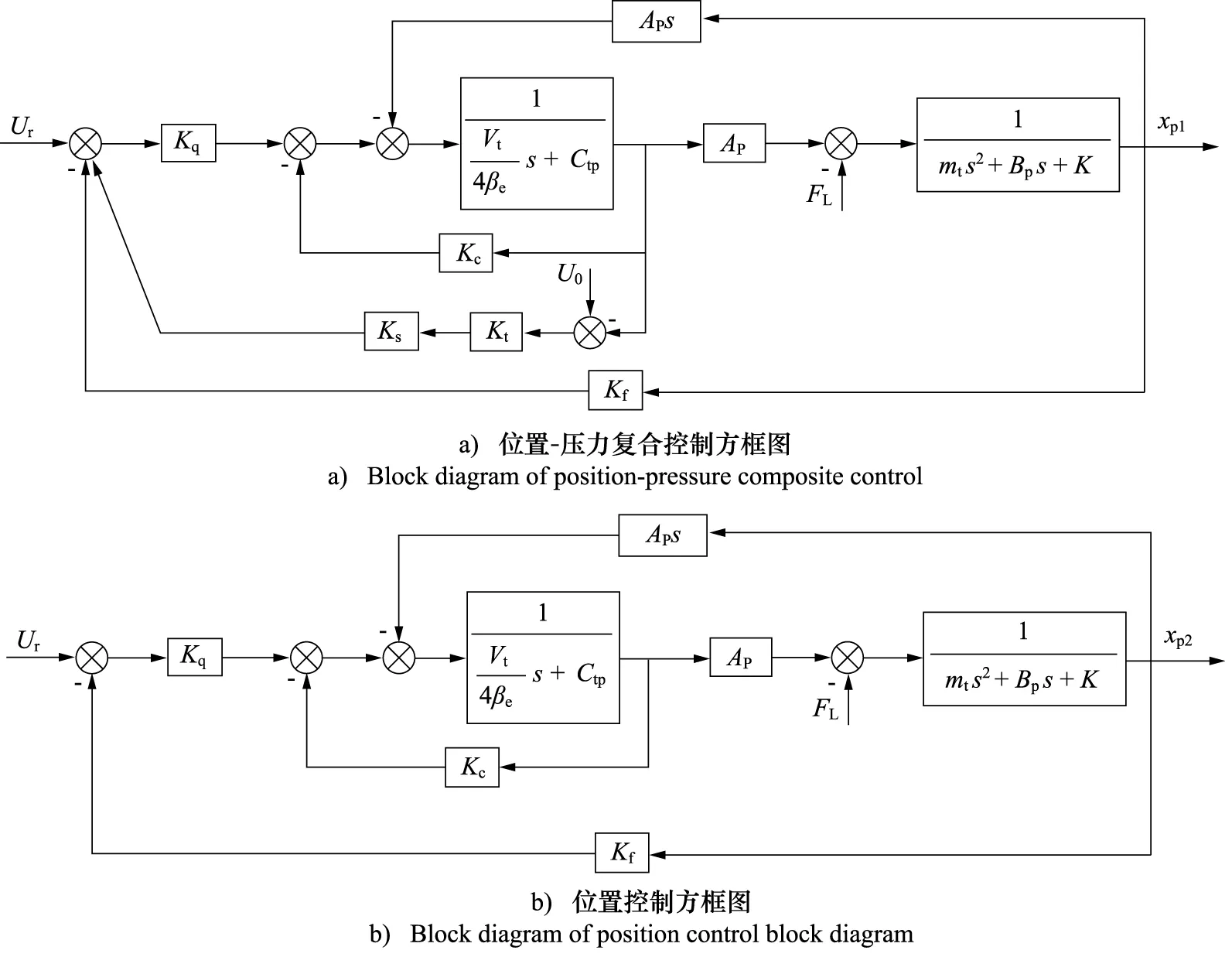
图3 旋压伺服系统方框图Fig.3 Block diagram of spinning servo system

|Ur-xp1|<|Ur-xp2|

因此，位置-压力复合控制精度更高，旋压后的表面质量更好。

2 仿真分析

根据旋压机工作过程，通过AMESim建立仿真模型，如图4所示，仿真过程中系统主要相关参数如表1所示，仿真时给定信号为1 mm的阶跃函数。

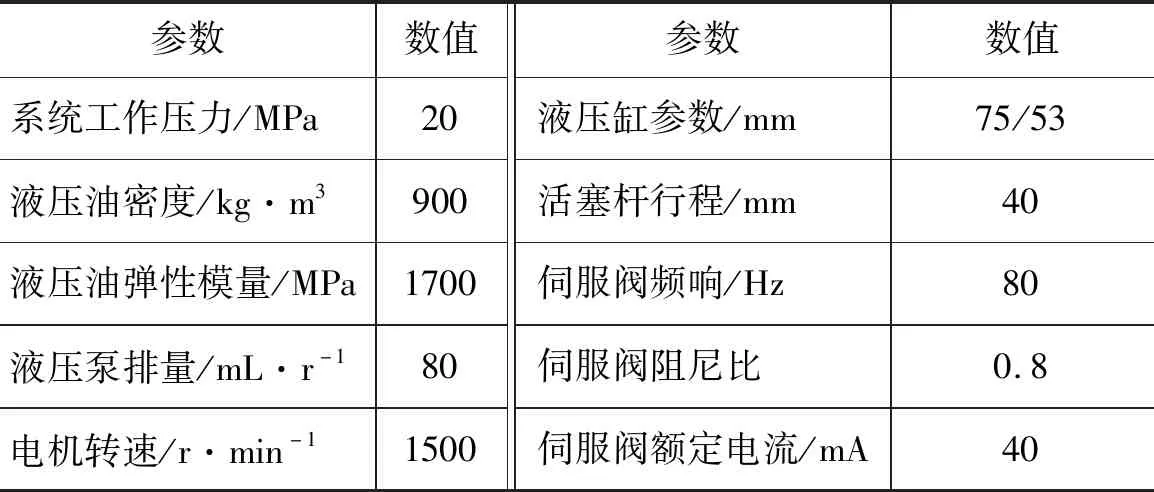
表1 旋压伺服系统仿真时各参数值Tab.1 Parameter values during simulation of spinning servo system

理想状态下，负载F恒定，F=20 kN时仿真结果如图5所示。曲线1为位置闭环控制时液压缸的输出位移，曲线2为位置-压力复合控制时液压缸的输出位移。负载刚开始作用于系统时，两种控制方式的响应曲线都存在滞后现象，曲线1比曲线2滞后性更明显，接近1 s时曲线2达到允许误差范围，说明复合控制系统的响应速度明显优于单闭环控制系统的响应速度，同时系统的跟踪性得到明显提高，液压缸更准确地运行到指定位置，旋轮的压下过程用时更短，提高了生产效率。

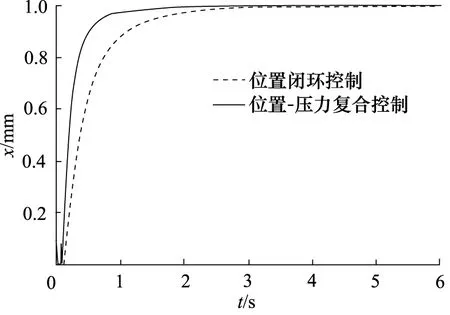
图5 液压缸活塞杆响应曲线Fig.5 Response curve of hydraulic cylinder piston rod

实际旋压过程中，由于干扰信号和其他不确定参数的影响，负载存在一定波动，实际负载F为(20000+10000sinπt) N，仿真结果如图6所示。

图6中虚线1为仅使用位置闭环控制时的响应曲线，实线2为位置-压力复合控制时的响应曲线。系统存在扰动时，位置控制下液压缸的位移偏差为0.05 mm，位置-压力复合控制下液压缸的位移偏差比位置控制时减小了近40%。说明位置-压力复合控制系统振荡程度减小、抗干扰能力强，同时系统的响应速度快、准确性高。

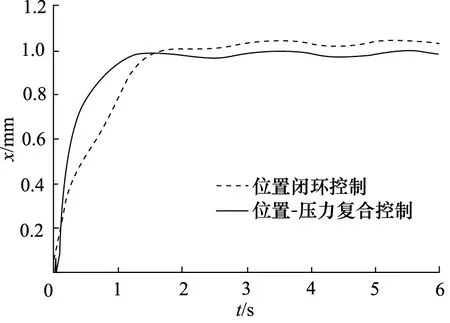
图6 液压缸活塞杆位移曲线Fig.6 Displacement curve of piston rod of hydraulic cylinder

从以上的仿真结果可以明显看出，采用位置-压力复合控制旋压机与单位置闭环系统相比，系统的迟滞性降低、响应速度快、抗干扰能力强，精度高。因此采用位置-压力复合控制的旋压机，可以提高工作效率，降低外负载扰动对系统控制精度的影响，提高钢管旋压的表面精度。

3 结论

为解决大直径薄壁管旋压过程中出现的压裂、压断等问题，提出采用位置-压力复合控制策略来提高旋压机工作过程中的位置控制精度、抗干扰能力，实现钢管旋压表面精度的提高。本研究首先建立旋压机液压系统的数学模型，然后通过AMESim软件进行仿真分析，得出结论如下：

(1) 旋压机液压系统采用位置-压力复合控制相比于位置闭环控制，能够降低系统的振荡程度、增强系统的抗干扰能力，提高系统的快速性、准确性；

(2) 该复合控制策略完全可行，可提高旋压机的工作效率，减小外负载扰动对系统控制精度的影响；同时旋压轮的进给量可达1 mm，可实现提高钢管旋压的表面加工质量和精度，为产品的开发研究提供了重要理论依据；

(3) 不影响系统稳定性的前提下，位置-压力复合控制简单、易实现，可被广泛应用于对位置控制精度要求比较高的液压伺服系统中。