液压软体抓手包络抓取接触力建模与实验
2022-08-06孙恩来吕浩斌
孙恩来,吕浩斌,王 滔
(浙江大学 海洋学院,浙江 舟山 316000)
引言
抓手作为自动化装备的重要组成部分,被广泛应用于工业、农业、医疗等领域。随着社会的不断发展,人们对抓手的性能要求也越来越高。软体抓手采用低模量材料制成,具有良好的载荷顺应性和环境适应性,降低了控制复杂程度,可与传统刚性结构的抓手形成互补,具有重要的潜在应用价值[1]。软体抓手的驱动方式主要包括流体驱动、线驱动、形状记忆合金驱动和电活性驱动等[2-5],其中流体驱动具有承载高、响应快等优点[6-10]。
参考人类抓取物体的习惯,抓手抓取可分为指尖抓取和包络抓取两种形式[11]。指尖抓取时抓手末端与物体接触,即点或线接触,适用于体积较小的物体;包络抓取时抓手通过自身柔顺形变将物体轮廓包裹住,即面接触,适用于体积较大的物体。目前对软体抓手指尖抓取的接触力建模已有较多研究,陈凌峰等[12]对软体抓手的指尖接触进行了力学建模,提出了一般化的指尖静态接触弹性模型。顾苏程等[13]建立了纤维增强型软体夹持器末端接触力与驱动压力、线圈匝数的关系并进行了实验验证。王峥等[14]分析了软体弯曲执行器末端接触力的产生机制,获得了压力、弯曲角度和接触力的关系。王滔等[15]根据液压软体执行器的指尖接触模型提出了一种接触力估计方法并应用于闭环控制。对于包络抓取,刘树峰等[16]设计了基于可变驱动容腔高度气动执行器的软体抓手,能够提供更大的抓取力,但未进行理论解析。
现有的软体抓手接触力建模主要以指尖抓取为主。抓手在包络抓取过程的受力状态复杂,关于接触力建模的研究也较为少见。本研究针对由波纹管状液压软体执行器构成的软体抓手,采用多连杆等效的方法建立了包络抓取接触力的简化模型,揭示了接触力与液压驱动压力的关系,并通过实验验证了模型的有效性。
1 液压软体抓手
软体抓手由对称分布的波纹管状液压软体执行器及结构件组成。软体执行器三维模型和剖面图如图1所示,当其内腔输入液压驱动压力后,由于波纹管侧和平面侧的形变不一致,将产生弯曲抓取动作。软体执行器实物采用热塑性聚氨酯弹性体橡胶3D打印而成,总体长度为123 mm,宽度为30 mm,厚度为13 mm。
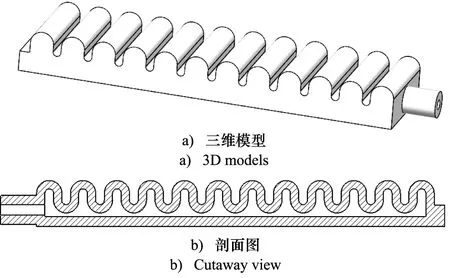
图1 液压软体执行器结构Fig.1 Hydraulic flexible actuator construction
2 包络抓取接触力模型
为简化分析,引入无摩擦接触和接触侧面为圆弧等刚性抓手研究中常用的假设[17-18],同时将软体执行器等效为一系列等距刚性铰接连杆,如图2所示,从连杆A起共有n个连杆与物体接触,第i个连杆对被抓取物体施加接触力Fi。分析可知当竖直向下抓取物体时,最大接触力在连杆A与被抓取物体作用点所在水平面。根据力和力矩关系,接触力对从连杆A起的各关节点力矩为:
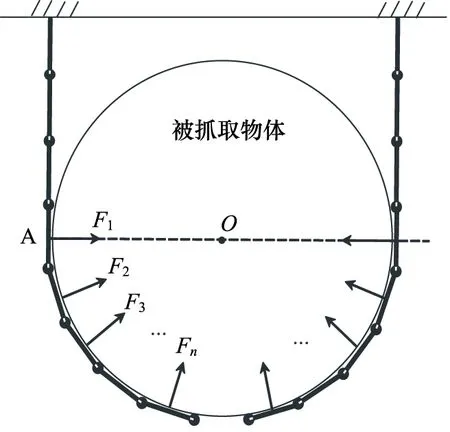
图2 等效刚性连杆包络抓取接触力分析示意图Fig.2 Schematic diagram of equivalent rigid linkage envelope gripping contact force analysis
(1)

根据式(1)可知,当各连杆关节转角θi和力矩Mi已知时,可计算出各接触力Fi。根据波纹管状软体执行器的形变机制,可将每个波纹视为独立的液压驱动容腔,如图3所示。
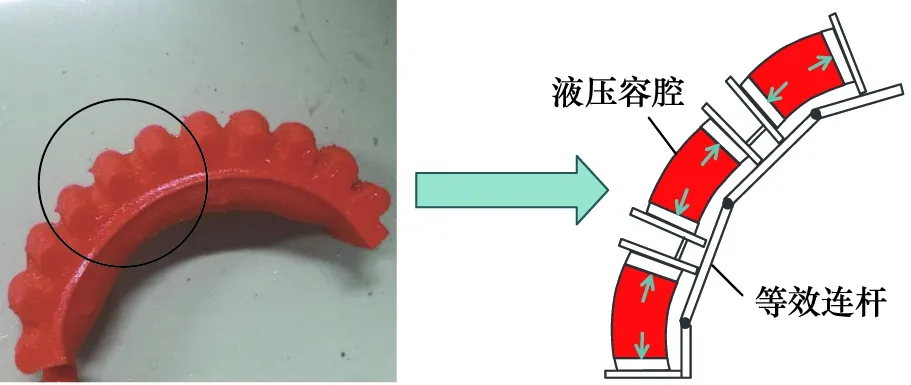
图3 波纹管状软体执行器的液压驱动示意图Fig.3 Schematic diagram of hydraulic drive of bellows soft actuator
对于液压软体抓手,当输入压力为0时,执行器保持初始无形变状态,未与物体接触;随着输入压力的增大,执行器逐渐弯曲动作,直到刚好包络接触物体,设此时内腔压力值为p,各关节转角为θi;随着输入压力的进一步增大,执行器弯曲角度不再变化,包络接触力从零开始增大,设容腔压力值为p+Δp,其中Δp为执行器接触物体后的压力增量,此时单个容腔的液压作用力为Fd。
以三容腔为例,液压容腔产生的驱动力矩如图4所示,具体表示如下:

图4 液压容腔产生的驱动力矩示意图Fig.4 Schematic diagram of driving torque generated by hydraulic chamber
Md3=FdH
(2)
Md2=FdH+FdLsinθ2
(3)
Md1=FdH+FdLsinθ1+Fd[Lsin(θ1+θ2)-
Lsinθ1+Lsinθ2]
(4)
式中,H为软体执行器容腔轴向中心线到关节轴的距离,液压作用力Fd可表示如下:
Fd=Δp·S
(5)
式中,S为软体执行器形变后各容腔的有效压力作用面积。
对于n个关节(n≥ 2),可对应获得各关节点的液压驱动力矩为:
(6)
式中,KT为各个液压作用力对应的力臂与有效压力作用面积乘积对应的矩阵,i=1,2,3,…,n-1。
由力矩平衡可得:
(7)
等效接触力向量可表示如下:
(8)
3 实验和结果分析
3.1 实验平台
为了检验液压软体抓手包络抓取接触力模型的有效性,设计了如图5所示的抓取目标物,主要由圆柱外壳和力传感器构成。外壳采用3D打印而成,力传感器为某传感器有限公司生产的LA-S1型号产品。液压软体抓手内部压力由电液驱动装置调节,并通过压力传感器实时测量,压力传感器为某公司生产的型号PSE574-01产品。
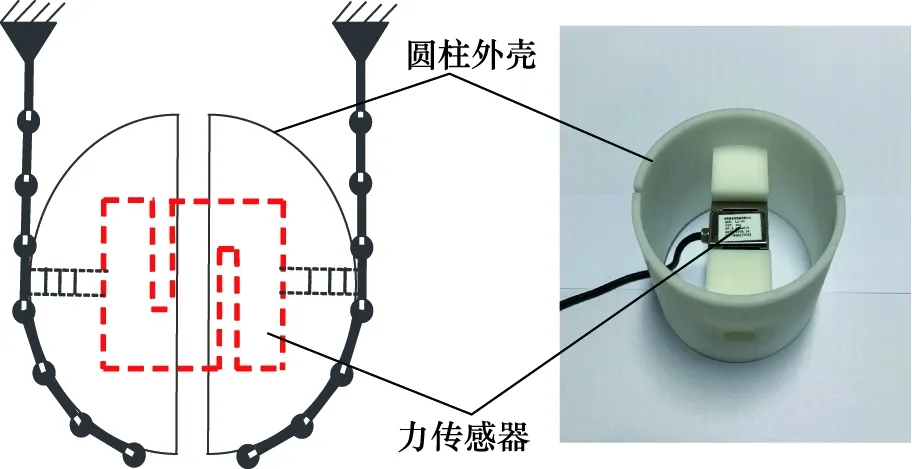
图5 包络抓取目标物的设计Fig.5 Design of envelope gripping targets
3.2 主要参数确定
模型中大部分参数可根据软体执行器和抓取目标物尺寸计算获得。由于黏弹性材料的非线性形变,软体执行器形变后各容腔的有效压力作用面积S难以解析计算,因此应用有限元分析软件ABAQUS和HyperView数值求解。针对热塑性软体材料,有限元分析采用Ogden应变能密度模型,其本构方程如下[19-20]:
(9)
式中,σ1为超弹性材料在主坐标系方向上的真实应力;D为模型的阶数;αi和μi为待定的材料模型参数;ε1为材料在主方向1上的应变。
为获得材料参数,根据ISO-37标准对材料试样进行了单轴拉伸试验,如图6所示。哑铃型试样以500 mm/min的速度拉伸至550%的拉伸率,共进行了5组试验,将结果平均值代入式(9)中,可得材料参数如下:N=3,α1=2.512,α2=3.681,α3=-3.344,μ1=-0.677 MPa,μ2=0.079 MPa,μ3=6.523 MPa。

图6 单轴拉伸试验Fig.6 Uniaxial tensile test
3.3 实验结果
包络抓取圆柱状目标物实验如图7所示,实验采用了3个不同尺寸的包络抓取目标物,其半径分别为40,45,50 mm。对于不同抓取目标物,分别测量了水平接触力随执行器内腔压力增量的变化曲线,同时根据接触力模型获得了理论计算结果。如图8所示为接触力模型计算结果和实验结果的对比,3组实验的平均误差分别为0.33,0.41,0.65 N,可见包络抓取接触力模型的计算结果与实验结果总体吻合,能够在一定范围内估计软体抓手包络抓取物体时的最大接触力。同时也需注意由于建模过程做了些理想化假设,导致模型计算结果与实验结果存在一定误差,如图8c中两者误差随着压力增量增大而加剧。

图7 包络抓取实验圆柱状目标物实验照片Fig.7 Envelope gripping experiments with cylindrical targets
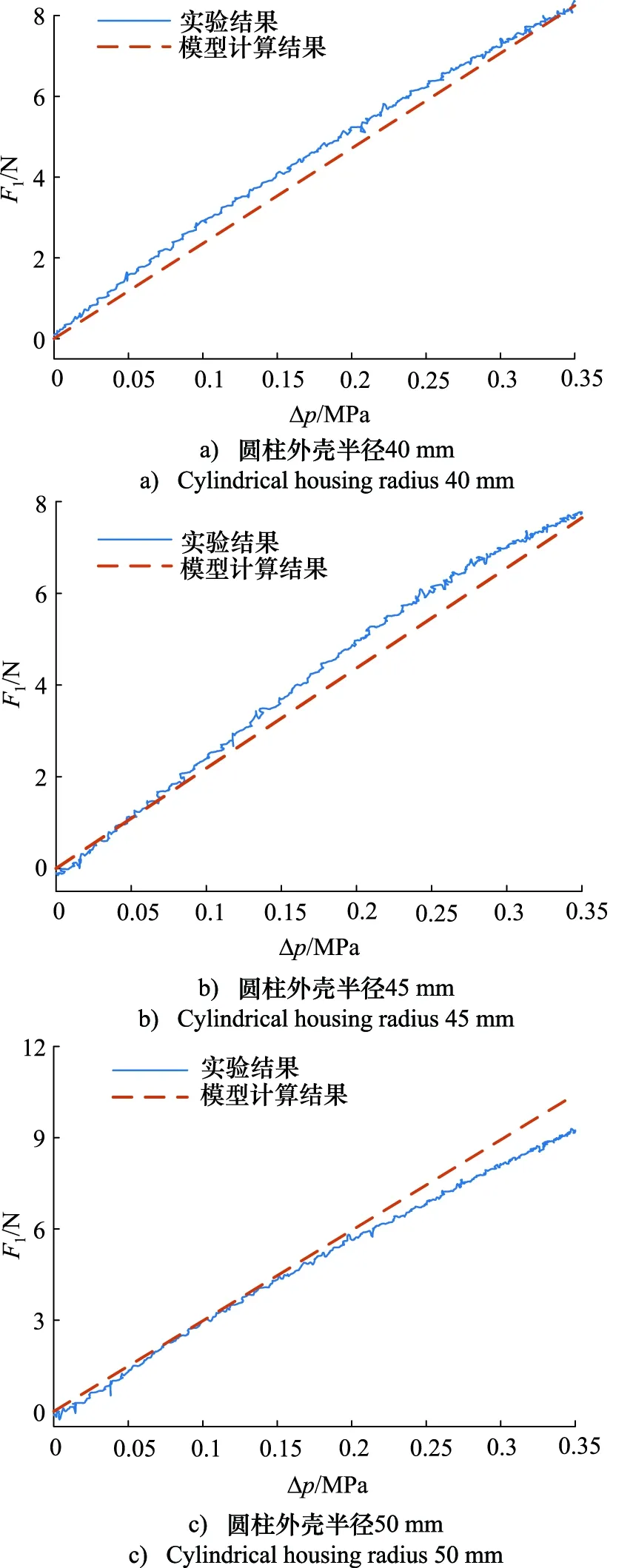
图8 包络抓取接触力模型计算结果与实验结果对比Fig.8 Comparison of calculated and experimental results of the envelope gripping contact force model
为了进一步验证包络抓取接触力模型的有效性,将模型获得的接触力估计值作为反馈,进行了接触力闭环控制实验。控制器采用比例-积分控制,接触力目标值包括梯形和阶梯形2种形式。实验结果如图9所示,可见接触力测量值能以良好的动态响应性能和稳态精度跟踪目标值。

图9 基于模型估计值的包络抓取接触力闭环控制实验Fig.9 Closed-loop control experiment of enveloping grasping contact force based on model estimated value
最后对液压软体抓手在包络抓取模式下的抓取能力进行了测试。如图10所示,采用双执行器构成的软体抓手,其自重约为80 g,在输入压力0.35 MPa时,测得可抓取的最大重量为1960 g,与自重的比值约为24.5∶1。

图10 最大抓取重量测试Fig.10 Maximum gripping weight test
4 结论
针对受力状态复杂的液压软体抓手包络抓取模式,提出了一种基于多连杆等效的接触力建模方法,并进行了实验验证。结果表明,包络抓取模式下可实现对较大体积物体的抓取,所建模型能够在一定范围内准确估计包络抓取接触力,可作为反馈值用于接触力闭环控制。
然而模型本身存在一定局限性,一是忽略了接触摩擦力,二是假设接触侧面为圆弧,因此还具有改进空间。
