热轧卷筒圆柱弹簧有限元分析

2022-08-06徐旭辉陈建军陈新刚

有色设备 2022年3期

徐旭辉,李勇,陈建军,全波,陈新刚,孙影

(衡阳中钢衡重设备有限公司,湖南衡阳 421002)

0 前言

地下卷取机多用于生产率很高的热连轧宽带钢的作业线上,是热轧带钢生产线上的重要设备,卷取机是热轧带钢生产线上的重要设备,卷取机的卷取能力直接影响着热轧生产线生产能力的发挥[1-2]。热轧卷筒采用连杆柱塞式结构(如图1 所示),主要由空心轴、扇形板、芯轴、连杆、柱塞和胀缩油缸、鼓型齿接手、前部延伸轴和轴承、干油润滑系统等组成[3]。工作原理:胀缩液压缸拉动芯轴,芯轴上的四棱锥面就可以推动柱塞装配(如图2 所示)沿空心轴的孔向外顶开扇形板,使卷筒胀开。为保证扇形板,柱塞装配和芯轴表面之间能够贴紧,在柱塞中装有压缩弹簧,在任一自由状态下,扇形板与柱塞并不直接接触,有0.5～2 mm 间隙,有效减少了带头的冲击。柱塞装配承受带材对卷筒的径向压力,而实际生产中由于热轧生产线条件恶劣,热轧卷筒在上机使用后出现弹簧失效或断裂现象时有发生(如图3 所示)。针对弹簧失效或断裂现象,本文进行了材料的机械性能和零件的受力分析,相应地改进了提高机械性能和热处理要求等方面,弹簧座也相应增加了润滑油、弹簧增加镀铬防锈工艺,有效改善了弹簧的使用效果。本文主要针对以上问题,对热轧卷筒上的弹簧进行分析,在实际工作中起到指导作用。

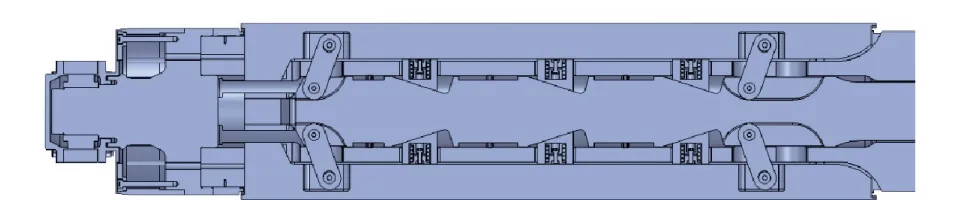
图1 热轧卷筒局部模型图

图2 柱塞装配模型和装配实物图

图3 弹簧断裂失效实物图

1 分析参数

在实际应用中,弹簧是常用的弹性零件和受力零件,它在受载后能够产生较大的弹性变形,吸收并储存能量。由于弹簧本身结构简单、制造方便,且具有高的比能容量。因此冶金行业应用广泛,特别在热轧地下卷取机卷筒中应用普遍。根据设计理念的不同,目前在热轧地下卷取机卷筒中应用的主要有圆柱压缩弹簧和矩形压缩弹簧。圆柱弹簧和矩形弹簧在压缩变形过程中,弹簧截面所承受的载荷包括剪应力、扭矩、转矩、压应力,加上弹簧钢丝有一定的曲率,其实际变形以及应力分布相当复杂。在热轧工况条件比较恶劣的条件下,使用中出现的失效原因多为疲劳断裂,为了克服疲劳断裂失效,则需要准确的分析弹簧受力时最大应力值及其出现的位置。所以研究圆柱压缩弹簧截面直径变化对分析弹簧受力时最大应力值及其出现位置具有指导作用,也便于在后续设计中优化改进。

2 理论分析

(1)根据圆柱螺旋压缩弹簧的设计[4-5],可知弹簧截面直径d:

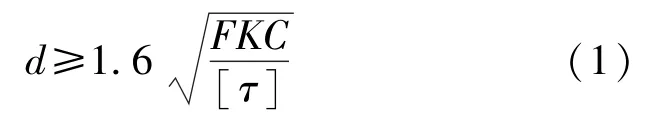
式中F—弹簧的最大工作载荷,N,取F=4 200 N;

K—弹簧曲度系数,K=

C—旋绕比,C=

D—弹簧中径,D=70 mm;

[τ]—弹簧丝内侧最大应力,MPa,其中[τ] ＜δs。

(2)根据圆柱螺旋压缩弹簧的设计,可知压缩弹簧变形量λ为:

式中G—弹簧材料的剪切模量,MPa,取G=80 000 MPa。

(3)弹簧在受轴向拉力或压力作用下,弹簧截面上剪切应力为:

根据以上设计要求,选择弹簧不同的截面直径d,通过有限元分析得出弹簧的位移和应力情况。

从以上计算公式可知,弹簧的截面直径d、弹簧的中径D、工作有效圈数n是最基本的结构参数,为简化分析过程,本文只将弹簧的截面直径d作为变量,其余参数按设计要求确定,从而得出弹簧受力时最大应力值和最大变形量与截面直径d变化的关系。

3 数值分析过程

3.1 创建几何模型

本论文分析的是圆柱形螺旋弹簧,取弹簧中径D=70 mm,外径D2≤89 mm,截面直径为d,弹簧有效圈数n=3(两端并紧并磨平),总圈数4.5,自由高度H=88.5 mm,弹簧材料参考50CrVA,材料密度7 850 kg/m3,屈服强度δs=450 MPa,抗拉强度δb=750 MPa,弹性模量E=200 000 MPa,剪切模量G=80 000 MPa。

比较多种有限元分析软件,由于在处理弹簧划分单元时,会遇到一些问题,比如对于不同方案,单元划分不好处理。建立分析模型采用的是Solidworks 建模[6](如图4 所示),建立模型后再导入ANSYS Workbench 中进行有限元分析。采用自由网格划分(如图5 所示)。模型建立通过螺旋线、扫描等功能建立一个变节距圆柱螺旋弹簧,并建立上下弹簧盖板模型,整体装配后如图3 所示。根据实际使用要求情况,约束条件:下底面采用全约束,上平面加载力F=4 200 N。此为导入ANSYS Workbench中进行有限元分析步骤:首先赋予弹簧和上下弹簧盖板材料属性,为简化分析,将弹簧和上下弹簧盖板材料设置成一致。并将下弹簧板进行整体固定约束,上弹簧板加载F=4 200 N 作用,通过改变弹簧截面直径d,来分析最大应力值和最大变形量变化值。

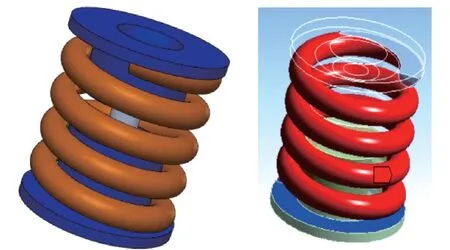
图4 柱塞受力分析模型和定义接触

图5 有限元分析模型

3.2 分析结果

拟定受力分析时采用以下的弹簧截面直径d=12 mm、13 mm、14 mm、15 mm、16 mm。选择以上弹簧截面直径值,主要考虑原设计采用截面直径d为14 mm,经过多年实际使用,不存在经常性断裂,只偶尔性失效或断裂。所以分析基于设计直径,并且可以通过对比进一步验证设计值是否可行。以下各图为通过有限元分析后得出的弹簧最大位移云图和最大等效应力云图。图6 为其他参数不变的情况下,只改变弹簧截面直径,弹簧在受力条件相同情况下的位移变化情况。图中显示弹簧截面积越小其变形越大,在同等力作用下,弹簧刚度随直径的增加而增加。通过分析可知弹簧截面直径不是越大越好,要结合设计条件及缓冲要求。图7 是其他参数不变的情况下,只改变弹簧直径,弹簧在受力一定情况下等效应力变化情况。图中显示弹簧所受等效应力随着弹簧截面直径增大而减少,但当弹簧截面直径达到一定值后,弹簧所受等效应力随着弹簧截面直径增大而出现增加现象,这主要是由于弹簧的压缩量逐渐减少,弹簧的受力主要集中在中间圈,以致于出现应力集中现象。

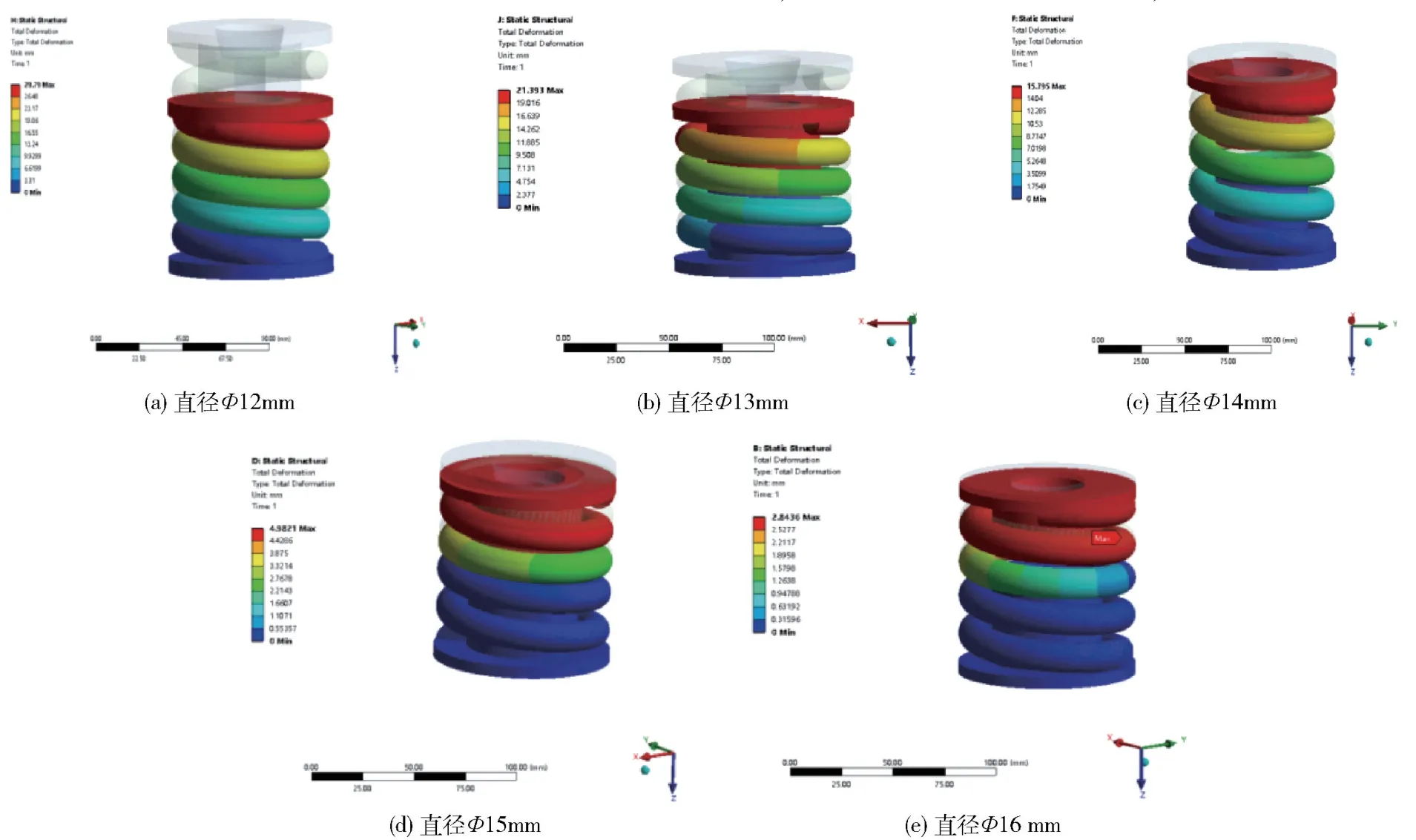
图6 位移云图

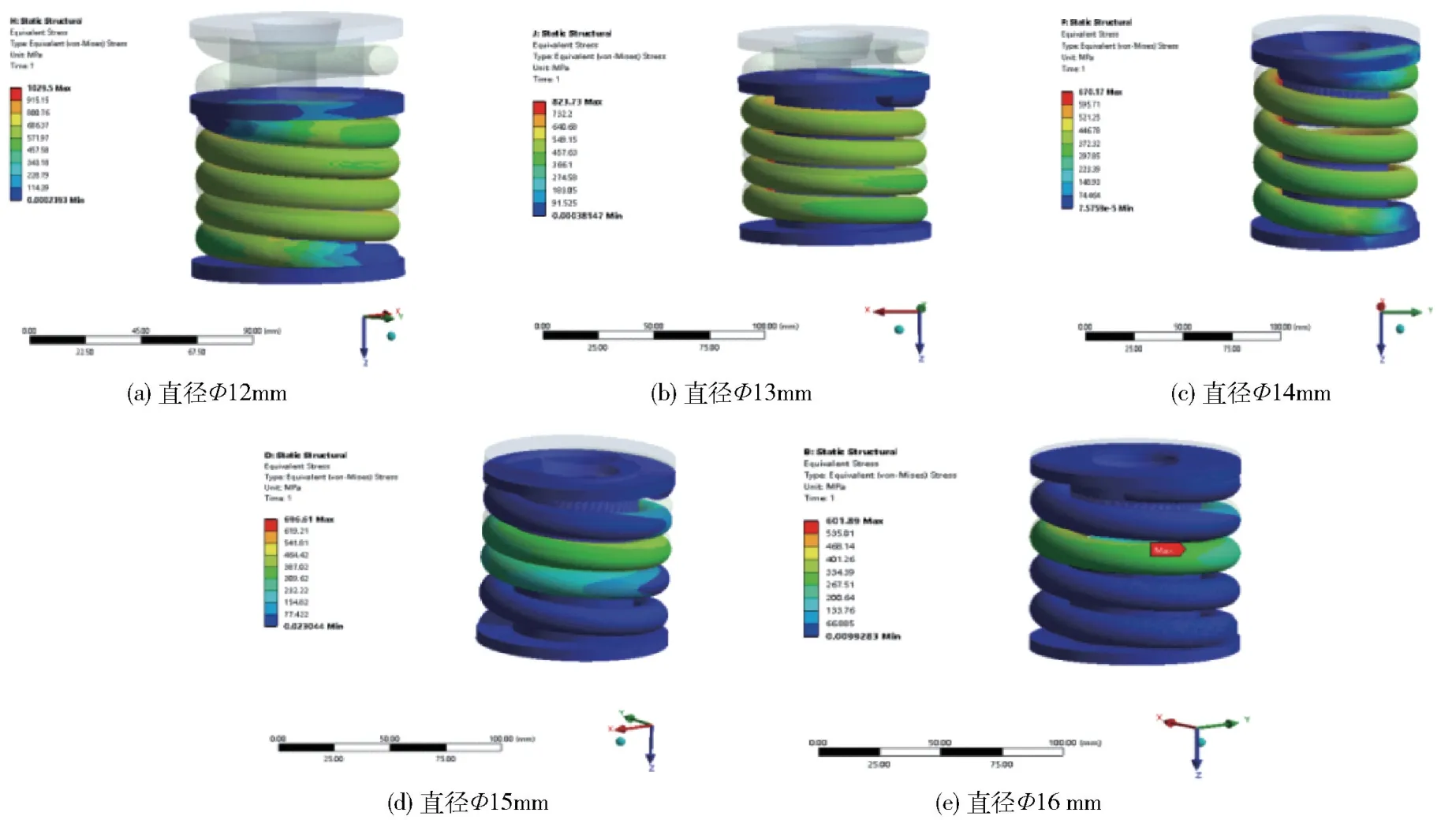
图7 等效应力云图

通过以上分析并结合图8 显示的最大变形量与弹簧截面直径关系曲线,可得出:当圆柱弹簧的自由长度和圈数等参数确定后,在一定的工作载荷作用下,弹簧钢丝的截面直径在一定区间从小到大变化时,弹簧的承载能力不断增强,弹簧的最大变形量随之明显减少。但是,当弹簧钢丝的截面直径增大到一定值后,继续增加弹簧钢丝的直径,因弹簧过硬(即刚度太大)时,弹簧的变形量变化明显减少。

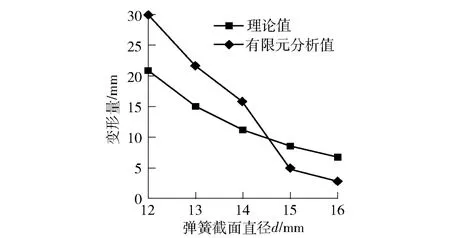
图8 最大变形量与弹簧截面直径关系

通过分析图9 显示的最大等效应力与弹簧截面直径关系曲线,可得出:在一定的工作载荷的作用下,弹簧的应力仅在一定区间内随弹簧钢丝直径的增加而减少。

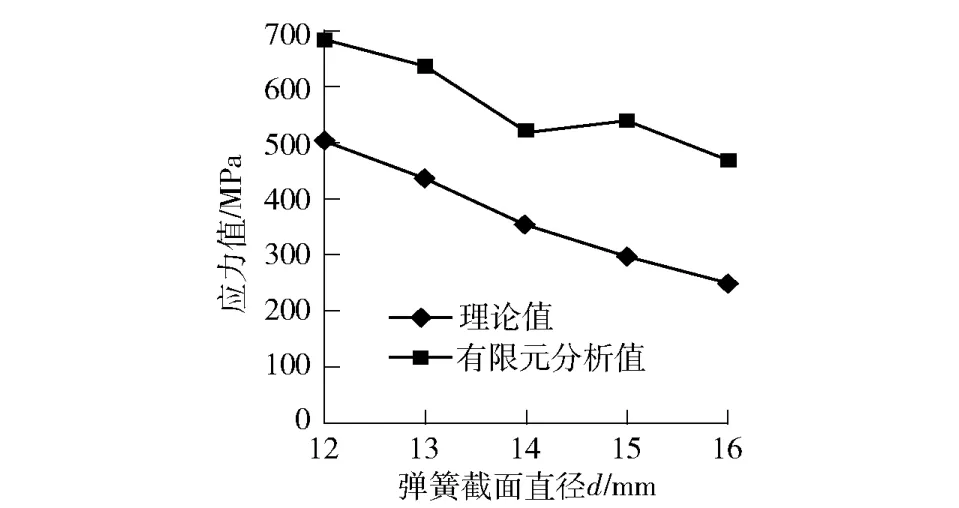
图9 最大等效应力与弹簧截面直径关系

综上所述,结合以上变化曲线,设计时可选择合适的弹簧钢丝直径,使弹簧既有合适的刚度又具有最小的内应力,从而达到弹簧最优化设计的目的。考虑到热轧地下卷取机卷筒使用时最大胀径Φ770 mm 到最小胀径Φ722 mm,正常卷取时是Φ762 mm。而连杆和柱塞是相互复合的一个动作,胀径时是通过柱塞和弹簧一起将扇形板顶开胀大。缩径动作时,则是由连杆完成。而承受的径向力主要是由柱塞和弹簧承受。通过分析,卷筒涨缩到正圆Φ762 mm 状态下,弹簧的预压缩量大(设计值10.7 mm),承受的径向力相对较大。从图中可以看出选择弹簧直径14 mm,最大变形量与最大等效应力均处于设计范围内,与实际设计相符合,对实际生产和使用起指导作用。