基于BPNN-NCT的风电机组主轴承异常辨识方法
2022-08-05刘昌杰张潇丹
刘昌杰,段 斌,张潇丹
基于BPNN-NCT的风电机组主轴承异常辨识方法
刘昌杰,段 斌,张潇丹
(湘潭大学自动化与电子信息学院,湖南 湘潭 411105)
风电机组主轴承作为传动系统的重要组成部件,其异常辨识精度受风速波动的影响较大。针对该问题,提出了一种基于BPNN-NCT的风电机组主轴承异常辨识方法。首先,利用相关系数法确定了与主轴承状态相关的参数作为模型的输入,并基于反向传播神经网络(BPNN)建立了以主轴承温度为状态参数的状态参数预测模型。然后,基于非中心(NCT)分布刻画了不同风速波动区间下状态参数预测残差的分布特性,并在此基础上提出了计及风速波动影响的风电机组主轴承异常状态量化指标。最后,以某风电场的2 MW直驱风力发电机组为例,验证了所提方法的有效性和准确性。
主轴承;状态参数;风速波动;预测残差;异常辨识
0 引言
风电机组长期运行在复杂多变的自然环境中,恶劣的环境导致机组各部件故障频发[1-4]。主轴承作为风电机组传动系统的核心部件,其是否能正常运行,将直接影响整个机组的安全性与稳定性[5]。由于持续受到交变冲击力和载荷作用的影响,主轴承极易发生故障[6-7]。主轴承一旦发生故障,其维修成本较高,停机运维的时间较长,造成的经济损失大[8]。对主轴承的状态进行监测,及时发现其异常,不仅能保证风电机组安全稳定运行,还能提升风电场的经济性。
风电场普遍安装了数据采集与监视控制(Supervisory Control and Data Acquisition, SCADA)系统。SCADA系统中存储了海量的自然环境与设备运行参数,通过挖掘其中的隐含信息辨识设备是否出现异常逐渐成为当前的研究热点[9]。当前基于SCADA系统数据的风电机组主轴承异常辨识,主要是通过建立正常状态下与主轴承状态相关的状态参数预测模型,根据检测残差的变化从而实现主轴承的异常辨识。当主轴承运行正常时,其状态参数的残差较小;当主轴承运行异常时,其状态参数的残差将明显增大。文献[10-11]基于SCADA系统数据,分别采用逐层编码网络和性能改善深度置信网络重构与主轴承状态相关的参数,并结合指数加权移动平均法监测重构残差,实现了主轴承的异常监测。然而风电机组的系统参数受环境的影响较大,采用上述方法需要重构的参数较多,极易因参数的剧烈波动而影响辨识结果。
温度作为轴承状态和负荷变化最敏感的参数[12],在轴承状态异常辨识中取得了较好的效果。文献[13]建立了正常状态下的主轴承温度多元线性回归(Multiple Linear Regression, MLR)模型,根据预测温度与实际温度残差的分布特性,定义了故障预测判别函数,实现了主轴承早期故障的预测。文献[14-15]分别采用深度信念网络(Deep Belief Network, DBN)和极限学习机(Extreme Learning Machine, ELM)建立了主轴承正常行为的温度预测模型,并基于核密度估计法确定了异常阈值,实现了主轴承的异常状态监测。为提高温度的预测精度,文献[16]组合多元线性回归模型、灰色预测模型和支持向量机模型建立了温度预测模型,并结合预测残差的分布特性,通过对比预测残差均值与标准差的置信区间来判断主轴承是否出现异常。
上述研究主要是通过挖掘SCADA系统数据构建状态参数预测模型,并根据预测残差的分布特性整定异常状态的判定阈值,从而实现主轴承状态异常或潜在故障的辨识[17]。然而上述研究存在以下问题:(1) 侧重于状态参数的预测精度研究[13-16],对状态参数残差的特性研究较少。在训练状态参数预测模型时,其目标是使预测误差最小,这使得表现较好的模型残差的分布较为集中,呈现出尖峰厚尾的分布特性。若采用高斯模型拟合残差分布特性[13],将使得拟合的误差较大。文献[14-15]采用核密度法拟合残差分布特性,虽然能够较为准确地反映残差的分布特性,但其拟合性能的好坏取决于带宽的选择,且核密度法在估计边界区域时存在边界效应[18],而在整定主轴承阈值时,残差两端的分布特性尤为重要,关系着异常辨识的精度。(2) 忽略了风速波动的影响。风电机组的运行参数与风速具有高相关性[19]。在预测风电机组系统参数时,其预测精度受风速波动的影响较大[20],仅依靠统计规律得到的预测残差分布特性而整定的单一阈值判别法难以综合体现设备状态异常信息,使得在风速剧烈波动及故障发展初期此类方法的辨识精度较低[21]。
针对上述问题,提出了一种基于BPNN-NCT风电机组主轴承异常状态辨识方法。该方法基于反向传播神经网络(Back Propagation Neural Network, BPNN)建立了以温度为状态参数的风电机组主轴承状态参数预测模型;根据预测残差分布的尖峰厚尾特性,提出了基于非中心(Non-centraldistribution, NCT)分布拟合主轴承状态参数残差的模型;考虑到风速波动对预测精度的影响,定义了衡量风速波动剧烈程度的指标,并在此基础上提出了计及风速波动影响的主轴承状态异常程度指标。以某风电场的2 MW直驱风力发电机组为例,验证了所提方法的有效性。
1 主轴承结构及其异常分析
风电机组主轴承由外圈、滚动体、内圈、保持架、连接螺栓和密封圈等部件构成,其外圈固定于轴承座,内圈连接着机械传动轴[22]。当风电机组运行时,主轴承内圈随着机械传动轴转动。主轴承通过机械传动轴支撑着风电机组的叶片、轮毂、变桨系统等部件,并承担着由它们质量产生的径向力与倾覆力矩以及风与叶片相互作用产生的轴向力、径向力和倾覆力矩[23]。由于主轴承吸收了绝大多数有害的负载和弯矩,并且持续地受到交变冲击力的影响,使得其极易发生故障。
主轴承常见的故障有内圈故障、外圈故障、滚动体故障和保持架故障[24]。主轴承从异常到发生故障的过程是一个累积过程。主轴承初始发生异常时,称为初级受损,包括腐蚀、磨损、疲劳等;接着是中级受损,包括散列和破裂;如果在此阶段还未对主轴承进行维护,最终将导致其难以修复。导致主轴承发生初级受损的主要原因有:在有害转矩下长时间运行,电腐蚀、润滑不良、温度过高等[25]。
当轴承发生初级受损时,其温度变化最为敏感[12]。因此将温度作为主轴承的状态参数,通过监测其变化能够实现主轴承异常状态的辨识[13-16]。
2 主轴承异常辨识模型
2.1 模型输入参数的选取
本文的数据来源于某风电场的10台2 MW直驱风力发电机2017年1—12月的运行数据,其中风电机组的编号为P1—P10。风电机组的基本参数如下:叶轮直径为115 m;切入风速为3 m/s;切出风速为25 m/s;运行数据的记录时间间隔为1 min。SCADA系统中记录的运行参数包括时间、风速、发电机输出功率、轮毂转速、发电机转矩、主轴承温度等。
SCADA系统中的参数众多,为了降低状态参数预测模型的复杂度,提高其预测精度,采用相关系数法选取与主轴承状态参数具有一定关联的参数作为模型的输入。相关系数的计算公式为

选取P1—P3号这3台风电机组1—12月的正常运行数据,计算状态参数与其他参数的相关系数,得到的部分相关系数数据如表1所示。采用相关系数大于0.6的参数作为模型的输入。因此,最终确定主轴承-1时刻温度、主轴承风轮侧温度、发电机输出功率、发电机转矩、轮毂转速、风速、机舱温度和测风塔环境温度这8个参数作为状态参数预测模型的输入参数。

表1 模型输入变量与主轴承状态参数的相关系数
2.2 基于BPNN的预测模型
BPNN是一种基于误差反向传播算法的多层前向神经网络,具有很强的非线性映射能力,能够表达复杂的映射关系[26]。典型的BPNN由输入层、隐含层和输出层构成[27],其训练过程可以分为两个阶段:第一个阶段是输入信号通过网络正向流动得到计算输出,称其为正向传播;第二阶段是将目标输出与计算输出的误差信号通过反向流动并更新神经元的权值和阈值,称其为反向传播[28]。BPNN的具体训练步骤如下所述。
1) 随机初始化各神经元的权值和阈值。
4) 根据式(2)—式(4)更新权值和阈值(反向传播)。



5) 判断是否满足设定的误差精度或者迭代次数,若满足,则停止训练,否则,返回步骤3)。
BPNN的结构直接影响模型的效果,合适的网络结构不仅能提高模型训练时的收敛速度,还能提高模型的精度。隐含层神经元的个数通常依据如式(5)所示的经验公式确定[29]。考虑到隐含层节点数一般为2的整数次方,结合经验公式,确定BPNN的隐含层节点数为8。
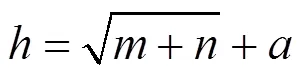
式中:为隐含层节点数;为输入层节点数;为输出层节点数;为常数,其取值为(1,10)。
为了得到更好的状态参数预测模型,以P1—P5号风电机组1—12月的正常运行数据作为训练集,以P6与P7号风电机组1—12月的正常运行数据作为测试集。对训练集和测试集均作归一化处理后,分别构建了单隐含层、双隐含层、三隐含层和四隐含层的BPNN,为防止BPNN出现局部最优,通过反复调节学习率和batch值,多次训练后,得到它们关于测试集的均方误差(MSE)、均方根误差(RMSE)和平均绝对误差(MAE),如表2所示。
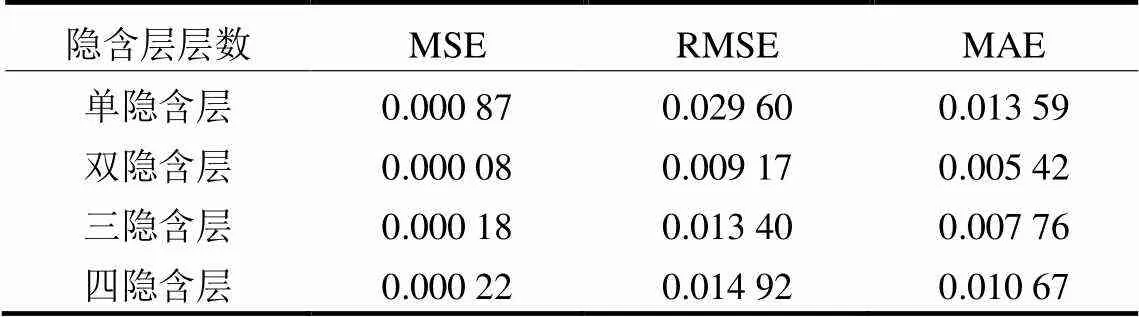
表2 不同隐含层BPNN模型的状态参数预测精度
由表2可以看出,双隐含层BPNN的MSE、RMSE和MAE的值均为最小,说明双隐含层的BPNN能够更为精确地预测状态参数,因此选取训练的隐含层节点数为8的双隐含层BPNN作为本文的主轴承状态参数预测模型。
2.3 残差的分布特性
2.3.1 NCT分布
NCT分布是一种非中心对称的连续分布[30],具有尖峰厚尾的特征,广泛地应用于统计推断、样本估计等领域[31]。NCT分布的概率密度函数为


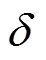
2.3.2考虑风速波动的残差分布特性
在预测风电机组系统参数时,其预测精度受风速波动的影响较大,预测残差的分布特性与风速具有高相关性[34]。在不考虑风速波动的影响下,直接拟合预测残差使得判定异常状态的阈值较为单一,难以满足系统动态变化的要求。
风速的波动性可以通过时间段内风速的离散程度来衡量。时间段内风速的离散程度越高,风速波动性越大,反之亦然。而标准差可以用来衡量一组数据的离散程度。因此,基于标准差定义了风速波动率,其计算公式为
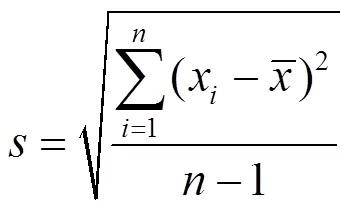
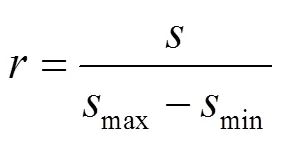
为了得到不同风速波动剧烈程度下状态参数残差的分布特性,本文将风速波动率划分为4个子区间。为保证各区间的样本量,首先需要对风速波动率的分布特性进行分析。以2.2节中的测试集为例,计算其风速波动率,由于其分布特性未知,故采用高斯核密度估计法拟合风速波动率的分布特性,得到其累积分布曲线如图1所示。
由图1可以看出,风速波动率的取值主要集中在(0.00, 0.18)。将风速波动率均分为4个区间,得到(0.00, 0.07)、(0.07, 0.12)、(0.12, 0.18)和(0.18, 1.00)这4个子区间。
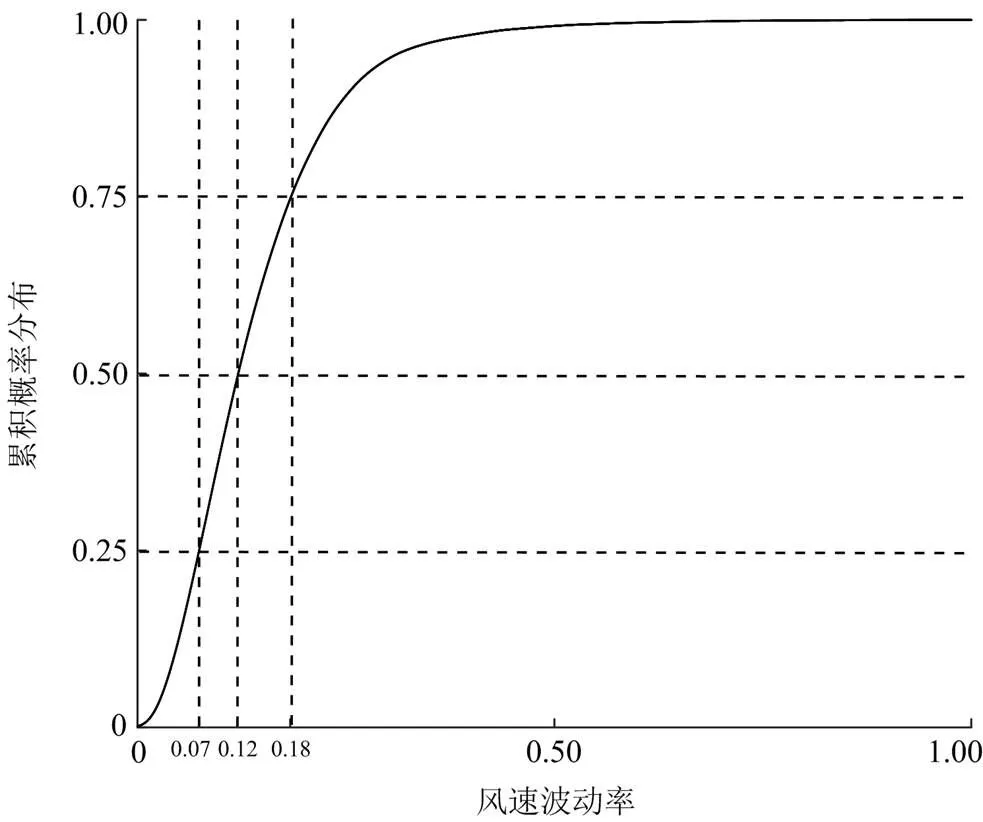
图1 风速波动率的累积分布曲线
以2.2节中测试集的残差为例,采用NCT分布拟合不同风速波动区间下的残差分布特性,得到其概率密度曲线如图2所示。

图2 主轴承状态参数预测残差的概率分布
由图2可以看出,不同风速波动区间下状态参数残差的概率密度曲线存在明显的差异,残差的分散性随着风速波动率的增大而增大;风速波动率越小,残差的分布越集中,其波动范围越小;风速波动率越大,残差的分布越分散,其波动范围越大。风电机组主轴承状态参数的残差与风速波动的剧烈程度有着紧密的联系,在整定主轴承状态异常判定阈值时不能忽略风速波动的影响。
2.4 主轴承异常状态的量化
主轴承正常运行状态下的状态参数残差分布特性反应了其处于正常状态下的特征。主轴承运行正常时,状态参数的残差在小范围内波动,当残差较大时,主轴承异常的概率增大[14-16]。基于此,对预测残差的取值范围进行划分,以分位数0.025和0.975对应的残差值将其划分为2个区间,如图3所示。
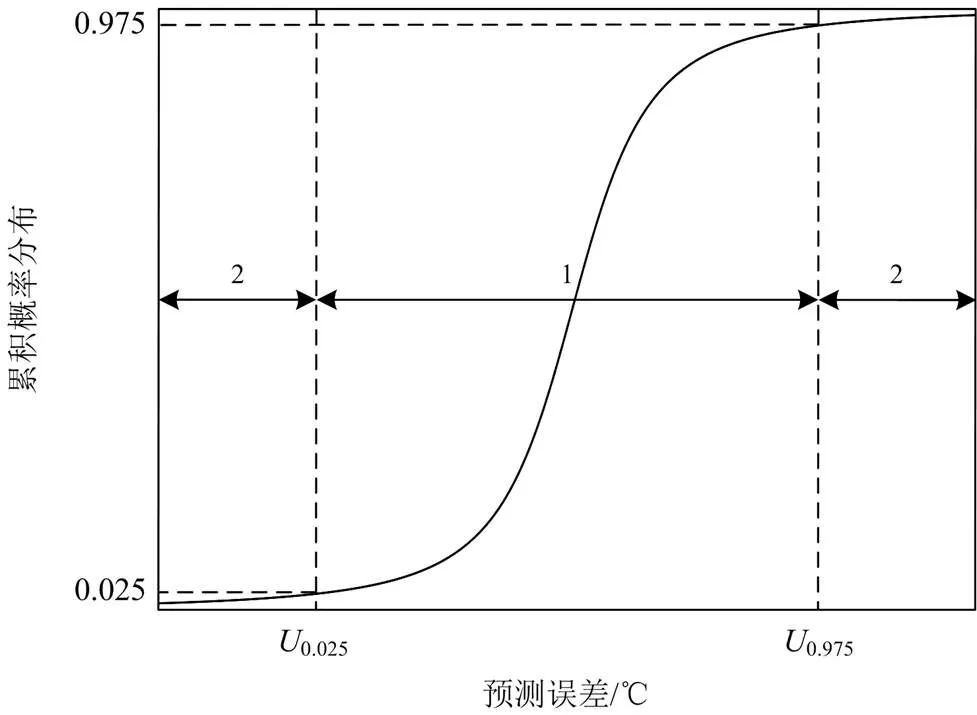
图3 状态参数预测残差的区间划分
采用滑动窗口统计状态参数预测残差落在两个区间的个数,其中窗口的宽度为20 min,窗口的移动步长为1 min。定义状态参数异常程度指数(Abnormal Level Index, ALI)来表征其异常程度,其计算公式为
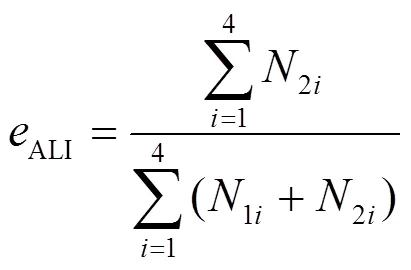
2.5 主轴承异常状态的辨识流程
图4为风电机组主轴承状态参数异常辨识流程。
基于BPNN-NCT的风电机组主轴承异常辨识的具体步骤如下。

2) 预测状态参数。根据输入参数,预测时刻主轴承的状态参数。
3) 计算残差和风速波动率。计算时刻主轴承状态参数的残差与-到时间段内的风速波动率。
4) 统计残差落入NCT分布中不同区间的数目。依据时刻计算的风速波动率,统计落入对应风速波动率下NCT分布中不同区间的残差数目。
5) 计算ALI。根据式(10)计算主轴承状态参数异常程度指数ALI。
6) 主轴承异常辨识。根据设定的ALI阈值判断主轴承是否异常。
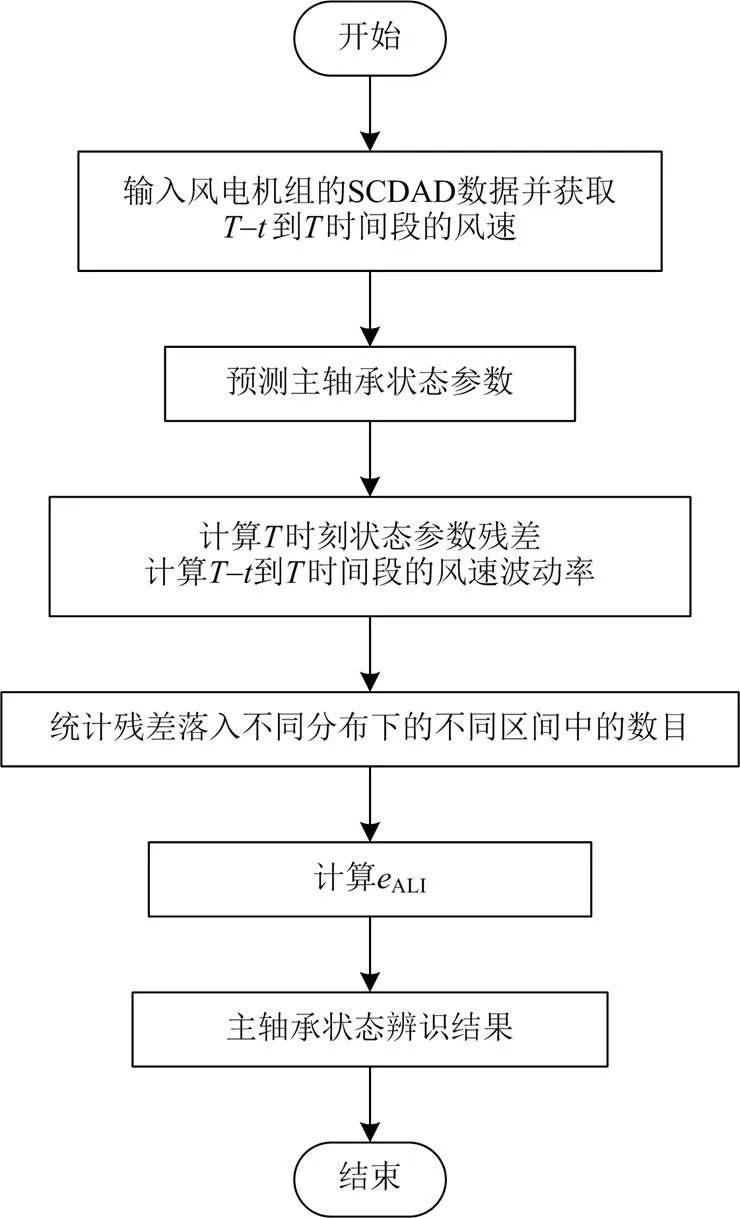
图4 主轴承异常辨识流程图
3 实例分析
3.1 状态参数预测模型的预测效果分析
为了验证基于BPNN的状态参数预测模型的预测效果,以P8号风电机组某日00:00—24:00的运行数据为例,预测主轴承状态参数,得到实际状态参数与预测状态参数的曲线和预测残差曲线如图5所示。
由图5可以看出,训练的模型能够很好地跟随实际的状态参数,且大部分数据的预测残差都小于0.2 ℃,表明基于BPNN的主轴承状态参数预测模型具有很高的预测精度。
3.2 基于NCT分布的残差拟合效果分析
为验证NCT分布拟合残差的效果,以P8与P9号风电机组1—12月的正常运行数据为例,采用高斯分布、柯西分布和高斯核密度分布,并引入拟合误差计算不同曲线的拟合误差,与NCT分布进行对比。得到各分布的拟合误差如表3所示,拟合曲线如图6所示。其中,拟合误差的计算公式为[18]
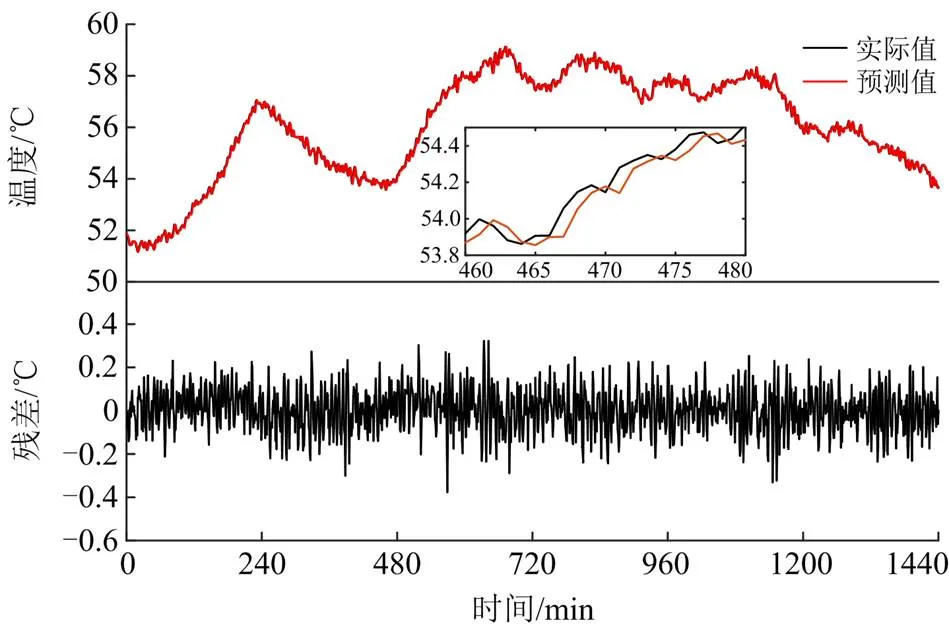
图5 状态参数预测模型的预测结果


表3 4种分布对主轴承状态参数残差的拟合误差
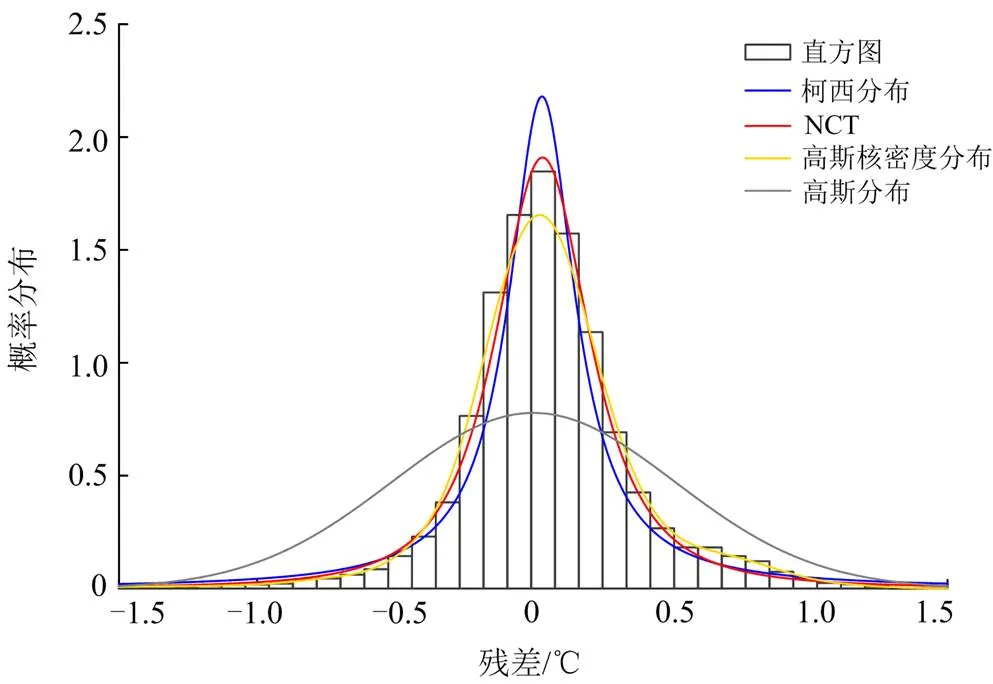
图6 4种分布对主轴承状态参数残差的拟合曲线
由表3和图6可以看出,高斯分布对残差的拟合程度最差;柯西分布虽能较为准确地刻画残差尖峰厚尾的特性,但对顶部的拟合程度较差;NCT分布和高斯核密度分布对残差的拟合误差相差较小,但高斯核密度分布对顶部的拟合程度较差,且在右端尾部产生了过拟合;而NCT分布能够准确地刻画残差的整体分布特性,拟合误差也最小。因此,采用NCT分布能够更加精确地反映主轴承状态参数残差的分布特性。
3.3 考虑风速波动的有效性分析
为验证考虑风速波动影响的有效性,首先利用训练的BPNN模型预测P8与P9号风电机组1—12月主轴承的状态参数,得到其状态参数的残差;然后根据2.3节中划分的风速波动区间,采用NCT分布分别拟合各风速波动区间的残差,并计算其0.025分位数和0.975分位数;最后得到不同风速波动区间下NCT分布区间的阈值如表4所示,其中(0.00, 1.00)表示忽略风速波动影响。
由表4可以看出,不同风速波动区间下,判定主轴承异常的阈值相差较大;当风速波动率在(0.00, 0.18)时,随着风速波动率的增大,阈值区间逐渐增大,说明随着风速波动率的增大,残差的分散性逐渐增大。当风速波动率处于(0.18, 1.00)时,结合图2分析可知,其分布曲线较为扁平,厚尾特征明显,因此相对波动区间(0.12, 0.18)的阈值范围有所减小。主轴承异常区间的判定阈值在考虑风速波动影响时与不考虑风速波动影响时相差较大。因此,在对主轴承异常状态进行辨识时不能忽略风速波动的影响。

表4 不同风速波动区间下状态异常的区间阈值
3.4 异常辨识案例分析
查阅风电机组主轴承故障数据报表,P10号机组在3月3日11:23—11:25因润滑不良使得轴承温度持续过高而停机。为了验证所提方案的有效性,对其进行仿真计算,得到主轴承ALI值的曲线如图7所示。
由图7可以看出,在11:13—11:35时段ALI值大于0.5,根据设定的状态异常阈值可以判定,在这个时间段内主轴承出现了异常。因此,所提方法能够实现主轴承的异常辨识。

图7 eALI时间序列
3.5 与传统方法的对比
为进一步验证所提方法的有效性,从该风电场的历史故障数据报表中选取了与主轴承故障相关的180个异常样本,并与传统采用MLR模型[13]、DBN模型[14]和ELM模型[15]的方法进行对比,结果如表5所示。
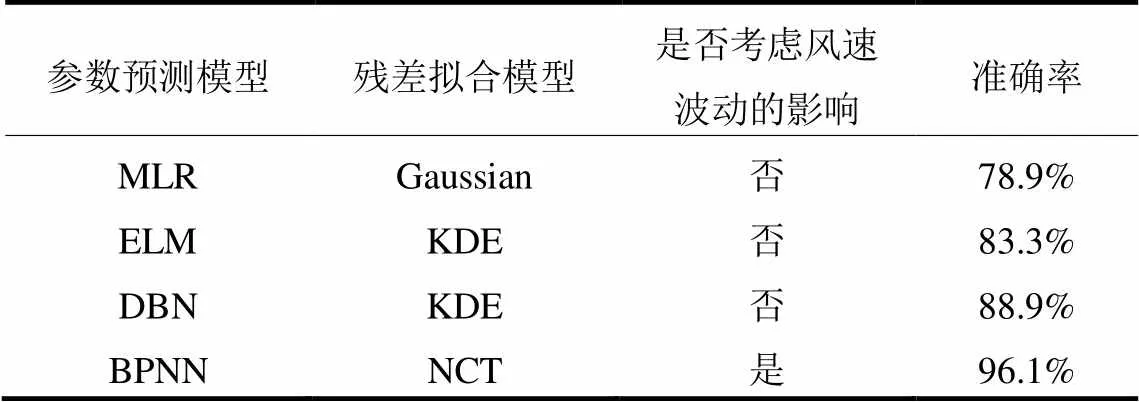
表5 不同方法的实验结果对比
由表5可以看出,本文所提的基于BPNN-NCT考虑风速波动的主轴承异常辨识方法的准确率明显高于其他方法。
4 结论
针对风电机组主轴承受风速波动影响而导致其异常辨识精度低的问题,提出了一种基于BPNN- NCT的风电机组主轴承异常辨识方法。经过实验与分析得到如下结论。
1) 采用NCT分布拟合主轴承状态参数残差,能够更加精确地反映其尖峰厚尾的分布特性,比传统的方法更精确。
2) 主轴承状态参数残差受风速波动的影响较大,不同风速波动区间下残差的分布具有明显的差异。风速波动的剧烈程度越大,其残差越分散。
3) 计及风速波动影响的风电机组主轴承异常辨识方法,不仅能满足系统动态变化的要求,还能提升主轴承异常辨识的精度。
[1] 陈俊生, 李剑, 陈伟根, 等. 采用滑动窗口及多重加噪比堆栈降噪自编码的风电机组状态异常检测方法[J]. 电工技术学报, 2020, 35(2): 346-358.
CHEN Junsheng, LI Jian, CHEN Weigen, et al. A method for detecting anomaly conditions of wind turbines using stacked denoising autoencoders with sliding window and multiple noise ratios[J]. Transactions of China Electrotechnical Society, 2020, 35(2): 346-358.
[2] 刘军, 汪继勇. 基于风电机组健康状态的风电场功率分配研究[J]. 电力系统保护与控制, 2020, 48(20): 106-113.
LIU Jun, WANG Jiyong. Research on power distribution of a wind farm based on the healthy state of wind turbines[J]. Power System Protection and Control, 2020, 48(20): 106-113.
[3] 常淼, 沈艳霞. 基于改进卷积神经网络的风电轴承故障诊断策略[J]. 电力系统保护与控制, 2021, 49(6): 131-137.
CHANG Miao, SHEN Yanxia.Fault diagnosis strategy of a wind power bearing based on an improved convolutional neural network[J]. Power System Protection and Control, 2021, 49(6): 131-137.
[4] 王杰, 彭志炜, 田宇, 等. 双馈风电机组故障穿越对系统暂态稳定的影响[J]. 电测与仪表, 2021, 58(5): 112-118.
WANG Jie, PENG Zhiwei, TIAN Yu, et al. Influence of fault ride-through of doubly-fed induction generators on transient stability of power systems[J]. Electrical Measurement & Instrumentation, 2021, 58(5): 112-118.
[5] 卢锦玲, 张祥国, 张伟, 等. 基于改进辅助分类生成对抗网络的风机主轴承故障诊断[J]. 电力系统自动化, 2021, 45(7): 148-154.
LU Jinling, ZHANG Xiangguo, ZHANG Wei, et al. Fault diagnosis of main bearing of wind turbine based on improved auxiliary classifier generative adversarial network[J]. Automation of Electric Power Systems, 2021, 45(7): 148-154.
[6] 张鑫, 徐遵义, 何慧茹, 等. 基于RBM和SVM的风电机组叶片开裂故障预测[J]. 电力系统保护与控制, 2020, 48(15): 134-140.
ZHANG Xin, XU Zunyi, HE Huiru, et al. Wind turbine blade cracking fault prediction based on RBM and SVM[J]. Power System Protection and Control, 2020, 48(15): 134-140.
[7] 黄南天, 杨学航, 蔡国伟, 等. 采用非平衡小样本数据的风机主轴承故障深度对抗诊断[J]. 中国电机工程学报, 2020, 40(2): 563-574.
HUANG Nantian, YANG Xuehang, CAI Guowei, et al. A deep adversarial diagnosis method for wind turbine main bearing fault with imbalanced small sample scenarios[J]. Proceedings of the CSEE, 2020, 40(2): 563-574.
[8] LIU Zepeng, ZHANG Long. A review of failure modes, condition monitoring and fault diagnosis methods for large-scale wind turbine bearings[J]. Measurement, 2020, 149.
[9] 马然, 栗文义, 齐咏生. 风电机组健康状态预测中异常数据在线清洗[J]. 电工技术学报, 2021, 36(10): 2127-2139.
MA Ran, LI Wenyi, QI Yongsheng. Online cleaning of abnormal data for the prediction of wind turbine health condition[J]. Transactions of China Electrotechnical Society, 2021, 36(10): 2127-2139.
[10]赵洪山, 刘辉海. 基于深度学习网络的风电机组主轴承故障检测[J]. 太阳能学报, 2018, 39(3): 588-595.
ZHAO Hongshan, LIU Huihai. Fault detection of wind turbine main bearing based on deep learning network[J]. Acta Energiae Solaris Sinica, 2018, 39(3): 588-595.
[11] 赵洪山, 刘辉海. 基于性能改善深度置信网络的风电机组主轴承状态分析[J]. 电力自动化设备, 2018, 38(2): 44-49.
ZHAO Hongshan, LIU Huihai. Condition analysis of wind turbine main bearing based on deep belief network with improved performance[J]. Electric Power Automation Equipment, 2018, 38(2): 44-49.
[12]周林, 赵杰, 冯广飞. 装备故障预测与健康管理技术[M]. 北京: 国防工业出版社, 2015.
[13] 张小田, 鄢盛腾, 周雪青, 等. 基于状态监测的风电机组主轴承早期故障预测方法[J]. 广东电力, 2012, 25(11): 6-9, 50.
ZHANG Xiaotian, YAN Shengteng, ZHOU Xueqing, et al. Early fault prediction method of wind turbine main bearing based on condition monitoring[J]. Guangdong Electric Power, 2012, 25(11): 6-9, 50.
[14] 王洪斌, 王红, 何群, 等. 基于深度信念网络的风机主轴承状态监测方法[J]. 中国机械工程, 2018, 29(8): 948-953.
WANG Hongbin, WANG Hong, HE Qun, et al. Condition monitoring method for wind turbine main bearing based on DBN[J]. China Mechanical Engineering, 2018, 29(8): 948-953.
[15] 何群, 王红, 江国乾, 等. 基于相关主成分分析和极限学习机的风电机组主轴承状态监测研究[J]. 计量学报, 2018, 39(1): 89-93.
HE Qun, WANG Hong, JIANG Guoqian, et al. Research of wind turbine main bearing condition monitoring based on correlation PCA and ELM[J]. Acta Metrologica Sinica, 2018, 39(1): 89-93.
[16] 郑玉巧, 魏剑峰, 朱凯, 等. 风力机主轴承故障监测方法[J]. 振动.测试与诊断, 2021, 41(2): 341-347, 415.
ZHENG Yuqiao, WEI Jianfeng, ZHU Kai, et al. Fault monitoring method of wind turbine main bearing[J]. Journal of Vibration, Measurement & Diagnosis, 2021, 41(2): 341-347, 415.
[17] KUSIAK A, VERMA A. Analyzing bearing faults in wind turbines: a data-mining approach[J]. Renewable Energy, 2012, 48: 110-116.
[18] 杨茂, 杜刚. 基于Location-Scale分布的风电功率概率预测研究[J]. 中国电力, 2017, 50(1): 140-145.
YANG Mao, DU Gang. Wind power probability prediction based onLocation-Scale distribution[J]. Electric Power, 2017, 50(1): 140-145.
[19] 沈小军, 周冲成, 吕洪. 基于运行数据的风电机组间风速相关性统计分析[J]. 电工技术学报, 2017, 32(16): 265-274.
SHEN Xiaojun, ZHOU Chongcheng, LÜ Hong. Statistical analysis of wind speed correlation between wind turbines based on operational data[J]. Transactions of China Electrotechnical Society, 2017, 32(16): 265-274.
[20] LI Zhi, YE Lin, ZHAO Yongning, et al. Short-term wind power prediction based on extreme learning machine with error correction[J]. Protection and Control of Modern Power Systems, 2016, 1(1): 9-16.
[21] SUN Peng, LI Jian, WANG Caisheng, et al. A generalized model for wind turbine anomaly identification based on SCADA data[J]. Applied Energy, 2016, 168: 550-567.
[22] 郭鹏, 王兆光. 基于高斯过程回归和双滑动窗口残差处理的风电机组主轴状态监测[J]. 电力自动化设备, 2018, 38(6): 34-40.
GUO Peng, WANG Zhaoguang. Wind turbine spindle state monitoring based on Gaussian process regression and double moving window residual processing[J]. Electric Power Automation Equipment, 2018, 38(6): 34-40.
[23] 张宏伟, 闫瑞志, 薛鹏, 等. 风电机组主轴承的设计与技术要求[J]. 轴承, 2014(4): 14-19.
ZHANG Hongwei, YAN Ruizhi, XUE Peng, et al. Design and technical requirements of main bearings in wind turbines[J]. Bearing, 2014(4): 14-19.
[24] 金晓航, 王宇, ZHANG Bin. 工业大数据驱动的故障预测与健康管理[J/OL]. 计算机集成制造系统: 1-12 [2021-07-28]. http://kns.cnki.net/kcms/detail/11.5946.TP.20200814.1703.006.html.
JIN Xiaohang, WANG Yu, ZHANG Bin. Fault prediction and health management driven by industrial big data[J/OL]. Computer Integrated Manufacturing System: 1-12[2021- 07-28]. http://kns.cnki.net/kcms/detail/11.5946.TP.20200 814.1703.006.html.
[25] 金晓航, 孙毅, 单继宏, 等. 风力发电机组故障诊断与预测技术研究综述[J]. 仪器仪表学报, 2017, 38(5): 1041-1053.
JIN Xiaohang, SUN Yi, SHAN Jihong, et al. Fault diagnosis and prognosis for wind turbines: an overview[J]. Chinese Journal of Scientific Instrument, 2017, 38(5): 1041-1053.
[26] 李国庆, 刘钊, 金国彬, 等. 基于随机分布式嵌入框架及BP神经网络的超短期电力负荷预测[J]. 电网技术, 2020, 44(2): 437-445.
LI Guoqing, LIU Zhao, JIN Guobin, et al. Ultra short-term power load forecasting based on randomly distributive embedded framework and BP neural network[J]. Power System Technology, 2020, 44(2): 437-445.
[27] 贾德香, 吕干云, 林芬, 等. 基于SAPSO-BP和分位数回归的光伏功率区间预测[J]. 电力系统保护与控制, 2021, 49(10): 20-26.
JIA Dexiang, LÜ Ganyun, LIN Fen, et al. Photovoltaic power interval prediction based on SAPSO-BP and quantile regression[J]. Power System Protection and Control, 2021, 49(10): 20-26.
[28] HAKIM S J S, RAZAK H A. Modal parameters based structural damage detection using artificial neural networks-a review[J]. Smart Structures and Systems, 2014, 14(2): 159-189.
[29] 姚仲敏, 潘飞, 沈玉会, 等. 基于GA-BP和POS-BP神经网络的光伏电站出力短期预测[J]. 电力系统保护与控制, 2015, 43(20): 83-89.
YAO Zhongmin, PAN Fei, SHEN Yuhui, et al. Short-term prediction of photovoltaic power generation output based on GA-BP and POS-BP neural network[J]. Power System Protection and Control, 2015, 43(20): 83-89.
[30] 杨贵金. 确定正态母体百分位值置信限的小样本方法及其应用[D]. 唐山: 河北理工大学, 2008.
YANG Guijin. A small sample method for determining the percentile confidence limit of a normal population and its application[D]. Tangshan: Hebei Polytechnic University, 2008.
[31] 汪鹏, 周基元. 非中心分布非中心参数的最大似然估计[J]. 统计与决策, 2014(15): 9-13.
WANG Peng, ZHOU Jiyuan. Maximum likelihood estimation of noncentral parameters of noncentraldistribution[J]. Statistics and Decision, 2014(15): 9-13.
[32] 王珺, 宋琼雅, 许岳培, 等. 效应量置信区间的原理及其实现[J]. 心理技术与应用, 2019, 7(5): 284-296.
WANG Jun, SONG Qiongya, XU Yuepei, et al. The principle and realization of the effect size confidence interval[J]. Psychological Techniques and Application, 2019, 7(5): 284-296.
[33] 金星, 洪延姬, 文明, 等. 非中心分布函数在可靠性下限计算中的应用[J]. 兵工学报, 2003(1): 82-84.
JIN Xing, HONG Yanji, WEN Ming, et al. Application of non-centraldistribution function in the calculation of reliability lower limit[J]. Acta Armamentarii, 2003(1): 82-84.
[34] YAN Cheng, TANG Yi, DAI Jianfeng, et al. Uncertainty modeling of wind power frequency regulation potential considering distributed characteristics of forecast errors[J]. Protection and Control of Modern Power Systems, 2021, 6(3): 276-288.
An abnormal identification method for the main bearing of wind turbines based on BPNN-NCT
LIU Changjie, DUAN Bin, ZHANG Xiaodan
(School of Automation and Electronic Information, Xiangtan University, Xiangtan 411105, China)
The main bearing of wind turbines is an important part of the transmission system, and its anomaly identification accuracy is greatly affected by wind speed fluctuations. To solve this problem, an abnormal identification method for the main bearing of wind turbines based on BPNN-NCT is proposed. First, the correlation coefficient method is used to determine the parameters related to the main bearing state as the input of the model, and a state parameter prediction model with the main bearing temperature as the state parameter is established based on a back propagation neural network (BPNN). Then a non-central(NCT) distribution is used to describe the distribution characteristics of the state parameter prediction residuals under different wind speed fluctuation intervals. Then a quantitative index of the abnormal state of the main bearing considering the influence of wind speed fluctuations is proposed. Finally, a 2 MW direct-drive wind turbine of a wind farm is taken as an example to verify the accuracy and effectiveness of the proposed method.
main bearing; state parameter; wind speed fluctuations; prediction residual; anomaly identification
10.19783/j.cnki.pspc.211178
国家自然科学基金项目资助(61379063);湖南省自然科学基金项目资助(2020JJ6034)
This work is supported by the National Natural Science Foundation of China (No. 61379063).
2021-08-29;
2021-11-17
刘昌杰(1995—),男,通信作者,硕士研究生,研究方向为风电设备状态监测;E-mail: lcj19951928@163.com
段 斌(1966—),男,博士,教授,研究方向为信息技术在电力系统中的应用,工程教育认证。E-mail: db61850@ 163.com
(编辑 许 威)
