多端混合UHVDC单极接地故障的半解析仿真法

宋 钊，刘鸿超，芮 智, 严 正

多端混合UHVDC单极接地故障的半解析仿真法

宋 钊，刘鸿超，芮 智, 严 正

(电力传输与功率变换控制教育部重点实验室(上海交通大学)，上海 200240)

针对现有特高压直流工程直流故障仿真模型未考虑控制系统以及其纯数值仿真速度慢的问题，提出了一种多端混合特高压直流工程的半解析仿真法。首先，在直流单极接地故障下，建立了考虑控制器动态的常规和柔性直流换流站实用模型。然后，进一步建立了典型三端混合特高压直流输电工程的直流单极接地故障仿真模型，并使用多阶段半解析法求解。多阶段半解析法的核心思想是将仿真时段均分成多个子区间，并在每个子区间上求近似解析解。该方法融合了解析方法和数值方法的优势，并有利于开展并行计算。最后，将所得结果与PSCAD/EMTDC、欧拉法和4阶龙格库塔法等常用数值解法进行比较。结果表明，所提方法能得到与PSCAD/EMTDC高度吻合的仿真波形，且速度远快于常用数值解法。

柔性直流；特高压直流；多阶段半解析法；直流故障

0 引言

特高压直流(Ultra-High Voltage Direct Current, UHVDC)输电具有输送容量大、输电距离远等优势，目前已成为解决我国能源基地与负荷中心地理位置逆向分布问题的主要手段[1-6]。

多端混合特高压直流输电(Multi-Terminal Hybrid UHVDC, MTH-UHVDC)工程[7]同时含特高压混合桥[8]真双极模块化多电平变流器(Modular Multi-level Converter, MMC)和特高压双阀组串联[9]的12脉动电网电压换相换流器(Line Commutated Converter, LCC)[10-12]，是HVDC的较复杂形式。MTH-UHVDC直流故障具有重要研究价值，其中不对称的单极接地故障[13]发生概率高于极间故障[14]，建模难度也远大于极间故障。

目前，HVDC故障建模的主流方法是忽略控制系统，从而将换流站简化为RLC定常电路[15-20]。RLC等效方法成立的前提是系统为线性定常电路，在很短的故障时间内(如1 ms)，该模型能够较准确地计算故障电气量。但由于混合子模块MMC的故障穿越控制策略有较好的直流故障抑制能力，保护动作的时间延长到20 ms左右，控制系统对短路电流的影响不可忽略，系统不再是线性定常电路，不符合RLC方法应用的前提，因此在工程上无法接受RLC方法造成的误差。但由于MTH-UHVDC系统非常复杂，对该系统直流故障电磁暂态仿真的研究较少。文献[21]在研究MMC直流故障时引入了控制系统，但实际上先用RLC等效法求短路电流解析式，再代入控制系统求子模块投切情况，未体现控制器对短路电流的影响。

然而，控制器的引入使系统变为高度非线性，解析困难，故障分析必须依赖电磁暂态仿真[22-23]。但如果考虑全部控制器，会增加仿真的计算量。因此，在建模方面，急需一种考虑控制器动态但相对精简的实用模型；在求解方面，需要一套高效率且保证精度的仿真算法以实现高性能仿真。

电磁暂态仿真的本质是微分方程组求解，求解方法有解析方法和数值方法。解析方法结果准确，但工程问题往往难以解析；数值方法是通用方法，但计算量大、精度可能不足。而这两种方法结合而成的半解析方法，兼具准确性和通用性[24]。Adomian分解法[25]能给出微分方程组的幂级数解，通用性强，被广泛应用于微分方程组求解[26-28]。运用“数值”思想，将问题的求解区间分割为若干连续子区间；再运用“解析”思想，用Adomian分解法求每个子区间上的解析解，这样就构造出了一种半解析方法——多阶段半解析法(Multistage Semi-Analytical Method, MSAM)。

作为一种兼顾精度和速度的优秀算法，MSAM在电力系统仿真领域有一定的应用。文献[29-30]利用MSAM进行多机系统仿真，并表明MSAM不仅提升了仿真速度，而且具有和4阶龙格库塔(4thorder Runge-Kutta, R-K4)方法相当的精度。文献[31]利用MSAM研究单机-无穷大母线系统的振荡。文献[32]利用MSAM进行简单DC/DC变换器的仿真。MSAM在传统电力系统仿真中已有成熟应用，其在电力电子化电力系统(尤其是HVDC)仿真领域的应用，目前虽未见报道，但具有研究价值。

鉴于变流器RLC方法失效且详细模型计算量大，首先需要建立直流故障下MTH-UHVDC的实用模型。当发生直流故障时，MMC故障穿越策略和LCC定直流电流控制对直流故障过程影响显著。同时，MMC的直流电流远大于交流侧电流，电流环等其他交流量控制器对直流电气量特性影响不大，可以忽略。在准稳态模型下，LCC的交直流滤波器也可忽略。基于此思想，本文建立了直流故障下混合桥MMC和LCC的实用模型，利用MSAM求解系统故障电气量，并与PSCAD/EMTDC、欧拉法和R-K4的结果进行比较。仿真结果表明：

1) 在合适步长下，MSAM、欧拉法和R-K4都能得到与PSCAD/EMTDC基本吻合的结果，验证了实用模型的合理性。

2) 在建模方面，实用模型忽略了对直流电气量特性影响较小的控制器，从源头上减小了计算量。

3) 在求解方面，MSAM的数值稳定性优于欧拉法，仿真速度快于R-K4，具有与R-K4相当的精度。

1 直流故障下的换流站实用模型

在特高压直流工程中，由于MMC采用混合型桥臂并具有直流故障穿越策略，直流故障穿越的时间远大于纯半桥子模块MMC工程。因此，已有研究中不考虑控制系统作用，并将换流站主电路视为简单RLC支路的方法不再有效。分析特高压直流故障需要考虑控制系统，并针对直流故障工况合理简化的实用换流站模型。

1.1 特高压双阀组串联LCC的实用模型

特高压双阀组串联LCC(简称特高压LCC)是适用于UHVDC的LCC换流站。为了抬升直流侧电压和功率等级，一个特高压LCC包含2个直流侧串联的12脉动整流阀。特高压LCC的直流电压和交流电流可视为12脉动整流阀的2倍。

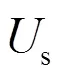
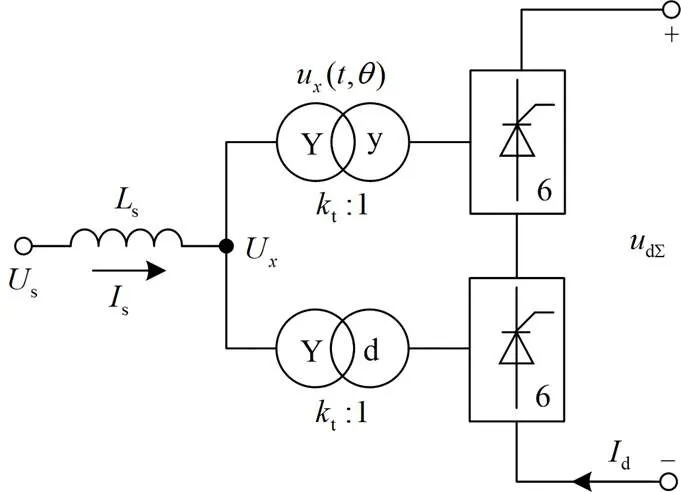
图1 12脉动整流阀

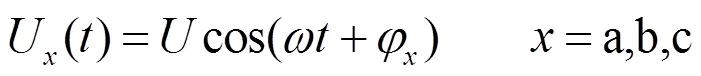
对应的Yy变压器和Yd变压器二次侧的电压为

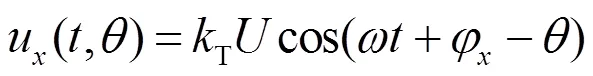
12脉动整流阀的交流侧电流为

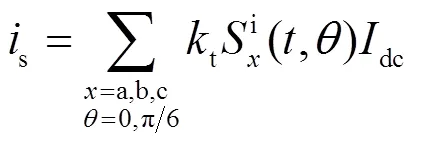
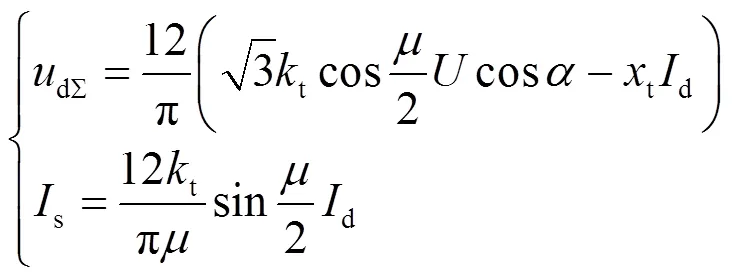
电网到PCC点的支路满足式(7)。

解得PCC点电压幅值为

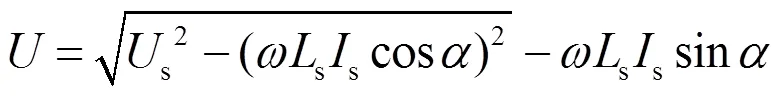
特高压LCC换流站由两个12脉动整流阀在直流侧串联、交流侧并联而成。特高压LCC的控制系统比较复杂，但对直流故障下波形产生主要影响的是定直流电流控制器[33]。整个换流站如图2所示。

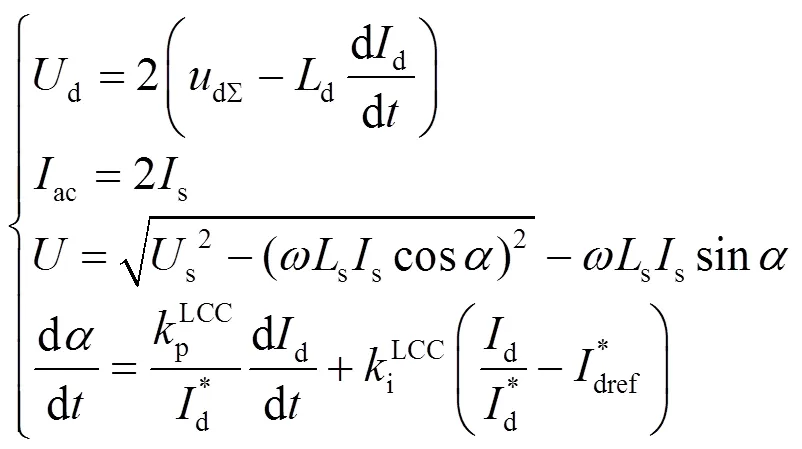
1.2 特高压混合桥真双极MMC的实用模型

特高压混合桥真双极MMC(简称特高压MMC)的实用模型如图3所示，它采用双阀组串联拓扑，一个桥臂由全桥和半桥两种子模块混合组成(共个)。图3中，MMC1给出等效电路，MMC2与MMC1相同，故仅用抽象框图表示。特高压MMC还具有故障穿越策略(图3中的绿色部分)，这是半桥MMC所不具备的。如引言所述，其他控制器(如电流环等)对直流故障影响不大，一律忽略。

图3 特高压MMC的直流故障实用模型

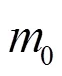
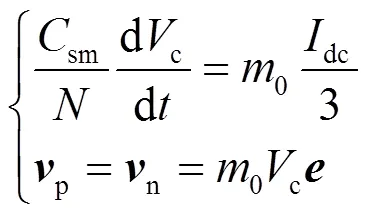
两个MMC三相桥臂的支路电压方程写成向量形式，如式(11)。

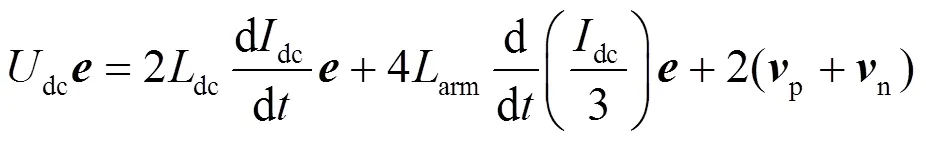
联立式(10)和式(11)，并结合故障穿越策略模型，可推出直流故障下特高压MMC的实用数学模型。

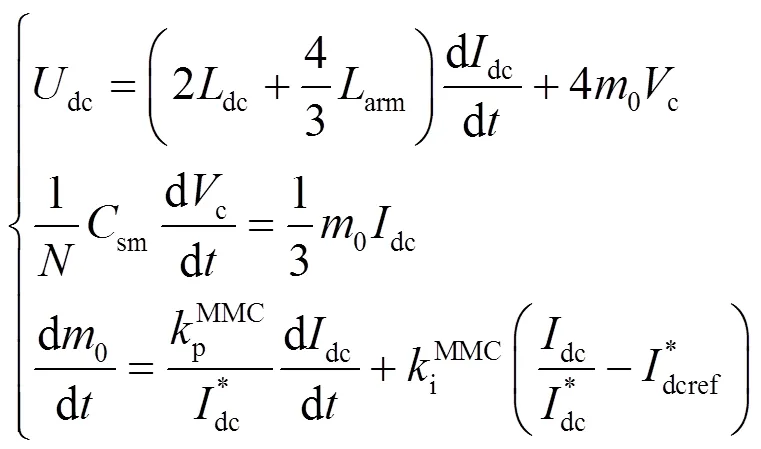
2 全系统直流故障模型

2.1 全系统结构

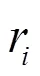
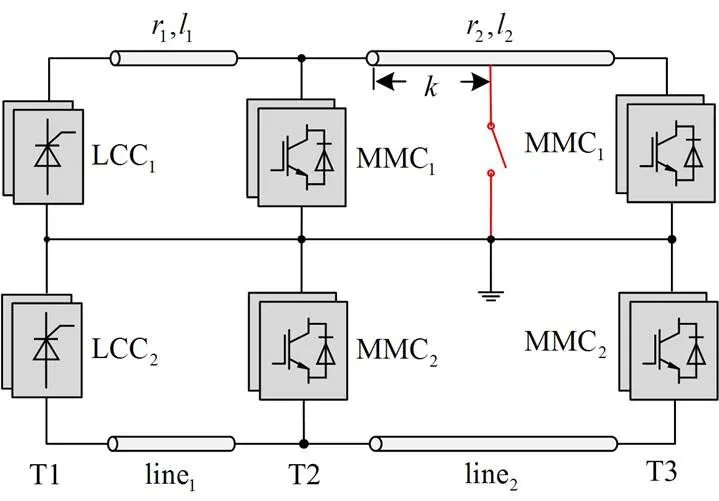
图4 三端特高压直流工程示意模型[32]

2.2 系统的简化等效电路

图5 直流故障实用等效电路

两部分电路的网孔电流方程为

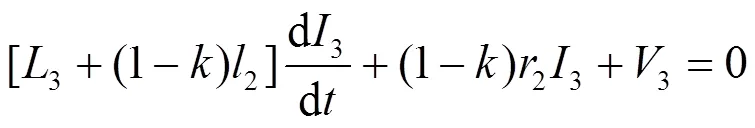
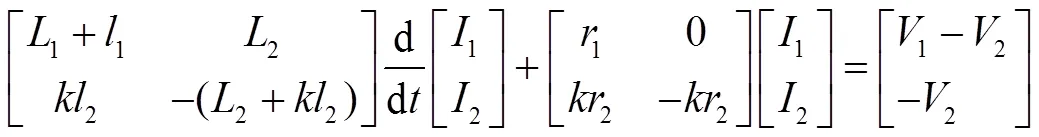
式(13)、式(14)和对应换流站的模型(式(9)、式(12))联立可构成微分-代数混合方程组，即为求解3个故障侧换流站直流电气量的完整数学模型。

3 直流故障下电气量的半解析解

经过代数变换后，第2节中的微分-代数方程组可变换为形如式(15)的一阶常微分方程组。

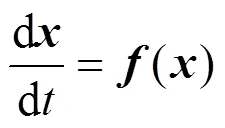
3.1 Adomian分解法简述[25]

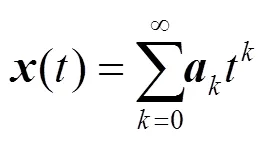
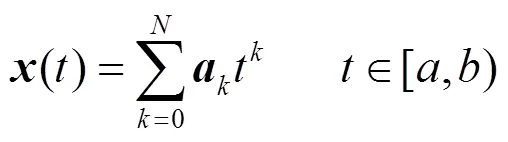
3.2 基于MSAM的电气量半解析解[36]

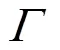
4 算例验证与结果分析

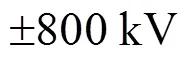
4.1 有效性验证

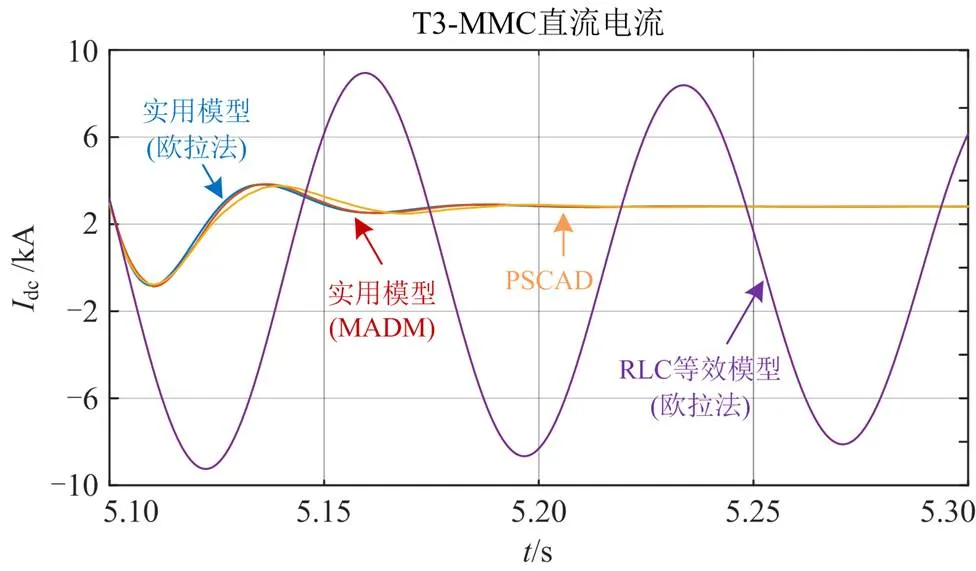
图6 实用模型与RLC等效方法的比较(Dt=0.1 ms)

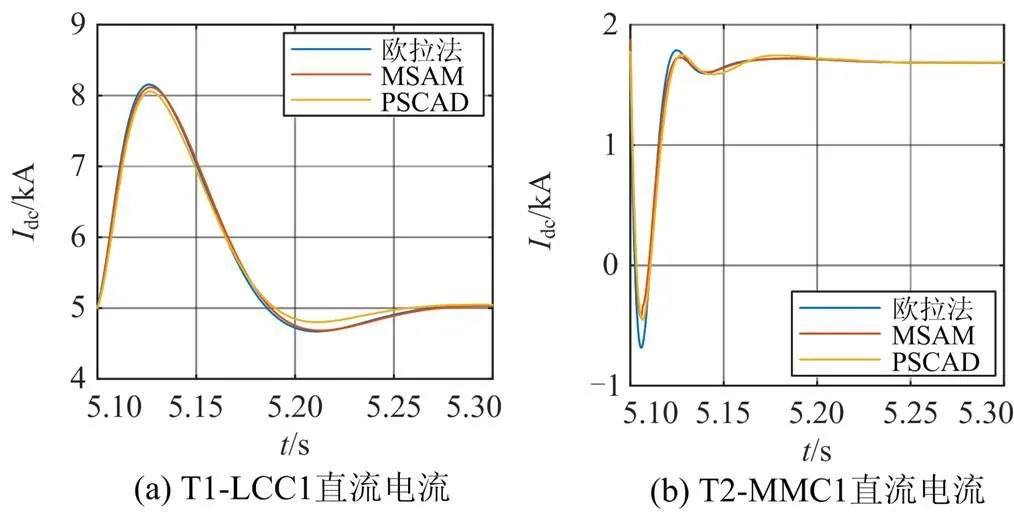
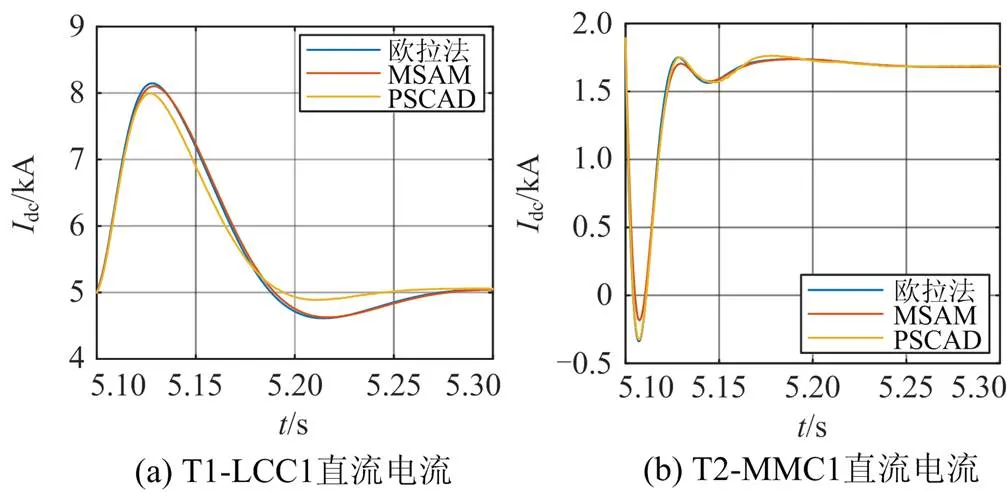
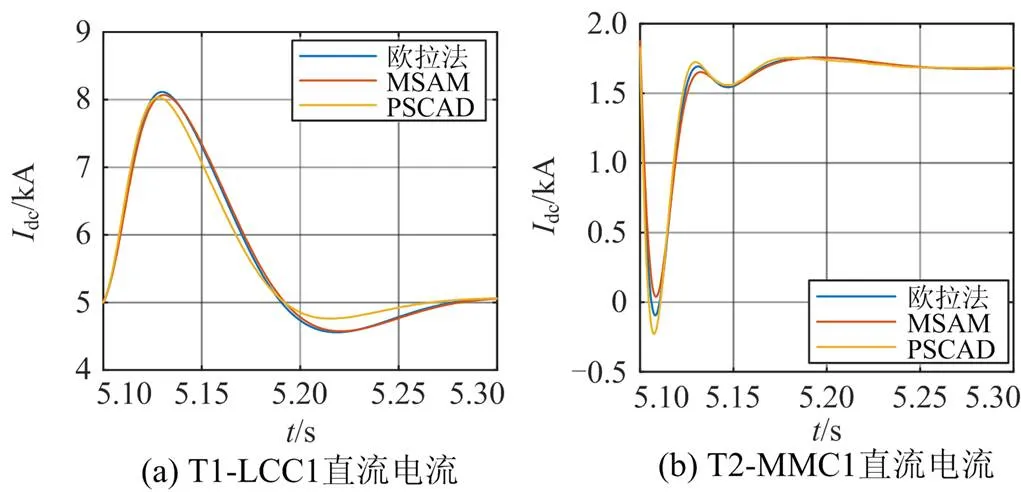
欧拉法、MSAM和PSCAD/EMTDC(参考组)3种方法所求得不同故障位置下的3个换流站故障电气量波形见图7—图9。在限流电抗器和控制系统的作用下，故障点移动对整个三端系统直流电气量波形和仿真误差的影响总体上不大。各电气量波形下三种方法所得结果吻合度均很好，MSAM和欧拉法对应的曲线基本贴合。

LCC直流电流的PSCAD/EMTDC结果与MSAM、欧拉法在两个极值点附近有少许偏离，这主要由于式(3)只考虑开关函数基波分量，而式(4)和式(6)是准稳态近似，造成一定误差。但全局最大相对误差仅为5.1%，且省去了繁琐的计算，利大于弊。

4.2 MSAM与常用数值解法的比较

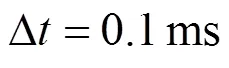
1) MSAM的数值稳定性优于欧拉法

图10为欧拉法的求解结果，在10 ms的步长下，求解结果发散，这是因为该步长超过了欧拉法的绝对稳定区间，舍入误差被放大和累积。将欧拉法改为相同步长的R-K4后才得到了正确结果。由图11可知，MSAM与R-K4误差相当。

2) MSAM的仿真速度优于R-K4

图10 欧拉法求解结果(Dt=10 ms, k=50%)

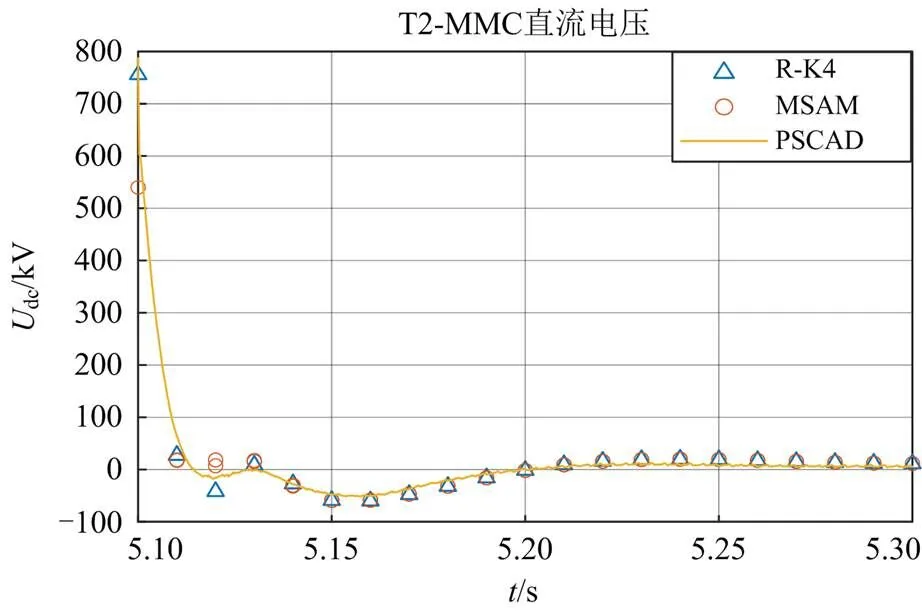
图11 MSAM和R-K4 结果对比(k=50%)

表1 MSAM和R-K4的仿真速度

另外，纯数值方法都需要串行迭代求解，但MSAM中各子区间边界处电气量值无数据依赖，利于并行计算[38]。这能进一步强化MSAM在仿真速度上的优势。

5 结论

本文首先针对MTH-UHVDC的直流故障场景，建立了考虑控制系统的特高压MMC和LCC的实用数学模型，并以三端混合UHVDC系统为例，形成系统的常微分方程组。然后，运用MSAM给出了该三端系统的半解析解，并和常用数值方法(欧拉法和R-K4) 以及PSCAD/EMTDC结果进行对比，结果表明：

1) 在常用仿真步长下，欧拉法、R-K4和MSAM均能得到满足工程允许误差的解，验证了实用模型的有效性。

2) MSAM的数值稳定性优于欧拉法，仿真速度快于R-K4且精度相当，体现了其优越性。

[1] 张爽, 李宏强, 王峰, 等. 基于电压源换流器的多端柔性直流输电系统拟交流最优潮流[J]. 电力系统保护与控制, 2020, 48(13): 31-37.

ZHANG Shuang, LI Hongqiang, WANG Feng, et al.Quasi-AC optimal power flow for voltage source converter-based multi-terminal DC system[J]. Power System Protection and Control, 2020, 48(13): 31-37.

[2] 周孝信, 陈树勇, 鲁宗相, 等. 能源转型中我国新一代电力系统的技术特征[J]. 中国电机工程学报, 2018, 38(7): 1893-1904, 2205.

ZHOU Xiaoxin, CHEN Shuyong, LU Zongxiang, et al. Technology features of the new generation power system in China[J]. Proceedings of the CSEE, 2018, 38(7): 1893-1904.

[3] 李培平, 周泓宇, 姚伟, 等. 多馈入结构背景下的高压直流输电系统换相失败研究综述[J/OL]. 电网技术: 1-17 [2021-07-19]. DOI: 10.13335/j.1000-3673.pst.2021.0945.

LI Peiping, ZHOU Hongyu, YAO Wei, et al. Review of commutation failure on HVDC transmission system under the background of multi-infeed structure[J/OL]. Power System Technology: 1-17[2021-07-19]. DOI: 10.13335/j.1000-3673.pst.2021.0945.

[4] 张怿宁, 陈可傲, 罗易萍, 等. 基于暂态电流相关系数的混合多端高压直流输电线路保护[J]. 电力建设, 2021, 42(5): 113-121.

ZHANG Yining, CHEN Keao, LUO Yiping, et al. Hybrid multi-terminal HVDC transmission line protection based on transient current correlation coefficient[J]. Electric Power Construction, 2021, 42(5): 113-121.

[5] 顾盈之, 叶鹏, 李中伟, 等. 直流输电系统电压静态稳定性研究综述[J]. 电子世界, 2020(19): 40-41.

GU Yingzhi, YE Peng, LI Zhongwei, et al. Review on voltage static stability of HVDC system[J]. Electronics World, 2020(19): 40-41.

[6] 杨楠, 崔伟, 王智伟, 等. 含风电特高压直流系统单极接地故障暂态特性研究[J]. 高压电器, 2020, 56(2): 142-149,157.

YANG Nan, CUI Wei, WANG Zhiwei, et al. Research on transient characteristics of monopolar grounding fault for wind power integrated UHVDC[J]. High Voltage Apparatus, 2020, 56(2): 142-149,157.

[7] 范琦, 张子露, 翟凯. 特高压多端混合直流输电实时数字仿真系统[J]. 电力电子技术, 2020, 54(6): 54-57.

FAN Qi, ZHANG Zilu, ZHAI Kai. Real-time simulation test system of UHV multi-terminal hybrid DC transition[J]. Power Electronics, 2020, 54(6): 54-57.

[8] LIU Y, CHEN Z. A flexible power control method of VSC-HVDC link for the enhancement of effective short-circuit ratio in a hybrid multi-infeed HVDC system[J]. IEEE Transactions on Power Systems, 2013, 28(2): 1568-1581.

[9] YIN Y, NING L, GAO L, et al. Research on balancing control technology of series dual valve groups in hybrid multi-terminal UHVDC transmission system[C] // 2019 IEEE 8th International Conference on Advanced Power System Automation and Protection (APAP), October 21-24, 2019, Xi'an, China.

[10]陈代忠, 王顺亮, 焦宁, 等. 基于动态相量法的电网换相换流器谐波传递研究[J]. 中国电机工程学报, 2021, 41(12): 4250-4261.

CHEN Daizhong, WANG Shunliang, JIAO Ning, et al. Research on harmonic transfer of line commutated converter based on dynamic phasors method[J]. Proceedings of the CSEE, 2021, 41(12): 4250-4261.

[11]李欣悦, 李凤婷, 尹纯亚, 等. 直流双极闭锁故障下送端系统暂态过电压计算方法[J]. 电力系统保护与控制, 2021, 49(1): 1-8.

LI Xinyue, LI Fengting, YIN Chunya, et al. Transient overvoltage calculation method of HVDC sending-end system under DC bipolar blocking[J]. Power System Protection and Control, 2021, 49(1): 1-8.

[12]张伟晨, 熊永新, 李程昊, 等. 基于改进VDCOL的多馈入直流系统连续换相失败抑制及协调恢复[J]. 电力系统保护与控制, 2020, 48(13): 63-72.

ZHANG Weichen, XIONG Yongxin, LI Chenghao, et al. Continuous commutation failure suppression and coordinated recovery of multi-infeed DC system based on improved VDCOL[J]. Power System Protection and Control, 2020, 48(13): 63-72.

[13] 谢仲润, 邹贵彬, 杜肖功, 等. 基于真双极的MTDC电网直流线路快速保护[J]. 中国电机工程学报, 2020, 40(6): 1906-1915.

XIE Zhongrun, ZOU Guibin, DU Xiaogong, et al. Fast DC lines protection for symmetrical bipolar based MTDC grid[J]. Proceedings of the CSEE, 2020, 40(6): 1906-1915.

[14] 王思华, 赵磊, 王军军, 等. 基于MMC的直流输电系统双极短路故障保护策略研究[J]. 电力系统保护与控制, 2021, 49(11): 9-17.

WANG Sihua, ZHAO Lei, WANG Junjun, et al. Research on protection strategy of a bipolar short circuit fault in an HVDC transmission system based on MMC[J]. Power System Protection and Control, 2021, 49(11): 9-17.

[15] LI Y, WU L, LI J, et al. DC fault detection in MTDC systems based on transient high frequency of current[J]. IEEE Transactions on Power Delivery, 2019, 34(3): 950-962.

[16] LETERME W, HERTEM D V. Reduced modular multilevel converter model to evaluate fault transients in DC grids[C] // 12th IET International Conference on Developments in Power System Protection (DPSP 2014), IET, March 31 - April 3, 2014, Copenhagen, Denmark.

[17] HAN P, WANG S. Parameter coordination of modular multilevel converter for robust design during DC pole to pole fault[C] // 2012 China International Conference on Electricity Distribution, IEEE, September 10-14, 2012, Shanghai, China.

[18] 梁远升, 黄泽杰, 李海锋, 等. 基于行波相位特性的三端混合直流线路行波保护原理[J]. 中国电机工程学报, 2021, 41(13): 4525-4543.

LIANG Yuansheng, HUANG Zejie, LI Haifeng, et al. Phase characteristics based travelling wave protection for transmission line of three-terminal hybrid HVDC system[J]. Proceedings of the CSEE, 2021, 41(13): 4525-4543.

[19] 夏仕伟, 高晨祥, 孙昱昊, 等. 含多种限流设备的柔性直流电网RT-LAB实时仿真建模[J]. 中国电力, 2021, 54(10): 28-37.

XIA Shiwei, GAO Chenxiang, SUN Yuhao, et al. Real-time modeling and simulation of flexible DC grid with various types of current limiting devices based on RT-LAB[J]. Electric Power, 2021, 54(10): 28-37.

[20] 李珅, 颜云松, 李晗, 等. 基于平衡理论的双端柔性直流输电系统降阶小信号建模[J]. 电力建设, 2020, 41(9): 115-123.

LI Shen, YAN Yunsong, LI Han, et al. Reduced-order small-signal model of double-terminal flexible DC transmission system applying equilibrium theory[J]. Electric Power Construction, 2020, 41(9): 115-123.

[21] 时熙, 程鹏. 计及控制策略影响的MMC-HVDC直流单极接地故障特性分析[J]. 电子科技, 2021, 34(8): 64-70.

SHI Xi, CHENG Peng. Analysis of MMC-HVDC DC single pole grounding fault considering the influence of control scheme[J]. Electronic Science and Technology, 2021, 34(8): 64-70 .

[22] 李高望, 陈锐智, 陈艳波. 考虑网络划分优化的交直流系统并行电磁暂态仿真研究[J]. 电力系统保护与控制, 2021, 49(4): 72-80.

LI Gaowang, CHEN Ruizhi, CHEN Yanbo. Research on parallel electromagnetic transient simulation of an AC-DC system considering optimization of network division[J]. Power System Protection and Control, 2021, 49(4): 72-80.

[23] SAAD H, JACOBS K, LIN W, et al. Modelling of MMC including half-bridge and full-bridge submodules for EMT study[C] // 2016 Power Systems Computation Conference (PSCC), June 20-24, 2016, Genoa, Italy: 1-7.

[24] 钟万勰, 欧阳华江. 解析法和半解析法的最新进展[J].大自然探索, 1993(2): 58-66.

ZHONG Wanxie, OUYANG Huajiang. The latest development of analytical and semi analytical methods[J]. Exploration of Nature, 1993(2): 58-66.

[25] ADOMIAN G. A review of decomposition method in applied mathematics[J]. Journal of Mathematical Analysis & Applications, 1988, 135(2): 501-544.

[26] JAFARI H, DAFTARDAR-GEJJI V. Positive solutions of nonlinear fractional boundary value problems using Adomian decomposition method[J]. Applied Mathematics & Computation, 2006, 180(2): 700-706.

[27] 贺少波, 孙克辉, 王会海. 分数阶混沌系统的Adomian分解法求解及其复杂性分析[J]. 物理学报, 2014, 63(3): 58-65.

HE Shaobo, SUN Kehui, WANG Huihai. Solution of the fractional-order chaotic system based on Adomian decomposition algorithm and its complexity analysis[J]. Acta Physica Sinica,2014, 63(3): 58-65.

[28] 骆兴国. Adomian分解方法及其最新进展[D]. 杭州: 浙江大学, 2006.

LUO Xingguo. Adomian decomposition method and its recent progress[D]. Hangzhou: Zhejiang University, 2006.

[29] NAN D, KAI S. Application of the Adomian decomposition method for semi-analytic solutions of power system differential algebraic equations[C] // 2015 IEEE Eindhoven PowerTech, June 29-July 2, 2015, Eindhoven, Netherlands.

[30] DUAN N, SUN K. Power system simulation using the multistage Adomian decomposition method[J]. IEEE Transactions on Power Systems, 2017, 32(1): 430-441.

[31] BETANCOURT R J, PEREZ M, BAROCIO E, et al. Analysis of inter-area oscillations in power systems using Adomian-Pade approximation method[C] // 2010 9th IEEE/IAS International Conference on Industry Applications-INDUSCON 2010, November 8-10, 2010, Sao Paulo, Brazil.

[32] GURRALA G, BATAGERI A, DINESHA D L. Real-time simulation of power converters using Adomian decomposition method on mini-FSS[C] // 2016 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), December 14-17, 2016, Trivandrum, India.

[33] YU X, YI J, WANG N, et al. Analysis on dynamic response of LCC-VSC hybrid HVDC system with AC/DC faults[C] // 2018 IEEE Innovative Smart Grid Technologies-Asia (ISGT Asia), May 22-25, 2018, Singapore, Singapore: 323-327.

[34] LIN W, JOVCIC D, NGUEFEU S, et al. Full bridge MMC converter optimal design to HVDC operational requirements[C] // 2016 IEEE Power and Energy Society General Meeting (PESGM), July 17-21, 2016, Boston, MA, USA.

[35] LIU Y, LUO G, YANG Y, et al. Adaptability analysis of traveling wave protection in multi-terminal hybrid DC transmission lines[C] // 2020 4th International Conference on HVDC (HVDC), November 6-9, 2020, Xi'an, China.

[36] RÈPACI A. Nonlinear dynamical systems: on the accuracy of Adomian's decomposition method[J]. Applied Mathematics Letters, 1990, 3(4): 35-39.

[37] BOYD J P, ALFARO L F. Hermite function interpolation on a finite uniform grid: defeating the Runge phenomenon and replacing radial basis functions[J]. Applied Mathematics Letters, 2013, 26(10): 995-997.

[38] PARK B, SUN K, DIMITROVSKI A, et al. Examination of semi-analytical solution methods in the coarse operator of parareal algorithm for power system simulation[J]. IEEE Transactions on Power Systems, 2021, 36(6): 5068-5080.

Semi-analytical simulation of a multiterminal hybrid UHVDC single-pole grounding fault

SONG Zhao, LIU Hongchao, RUI Zhi, YAN Zheng

(Key Laboratory of Control of Power Transmission and Conversion, Ministry of Education (Shanghai Jiao Tong University), Shanghai 200240, China)

There is a lack of a controller in existing DC fault simulation models of ultra-high voltage direct current (UHVDC) projects. Also their pure numeric simulation is slow. Thus a semi-analytical simulation method is proposed for a multiterminal hybrid UHVDC. First, practical models of both conventional DC and flexible DC converter are established considering controller dynamics. Secondly, a DC single-pole grounding fault simulation model for a typical three-terminal hybrid UHVDC is built and then analyzed using a multistage semi-analytical method (MSAM). In the MSAM, the simulation period is evenly divided into several small intervals, and an approximate analytical solution is obtained for each interval. The advantages of analytical methodology and a numerical algorithm are united in MSAM, where parallel computing is also easy to implement. Lastly, the simulation results of the MSAM are compared with those of PSCAD/EMTDC and common numerical methods (Euler method and 4th order Runge-Kutta method). The simulation waveforms of the MSAM match with PSCAD/EMTDC very well with a significantly higher simulation speed than the common numerical methods.

flexible DC; UHVDC; multistage semi-analytical method; DC fault

10.19783/j.cnki.pspc.211278

国家电网有限公司总部管理科技项目资助“基于数模混合仿真的柔性直流系统接入大电网的振荡特性及抑制措施研究”(5100-201955406A-0-0-00)

This work is supported by the Management Science and Technology Project of the Headquarters of State Grid Corporation of China (No. 5100-201955406A-0-0-00).

2021-09-16；

2022-01-22

宋 钊(1998—)，男，硕士研究生，研究方向为高频无线能量传输系统；E-mail: szh-98@sjtu.edu.cn

刘鸿超(1996—)，男，硕士研究生，研究方向为电力电子化电力系统电磁暂态仿真、稳定性分析；E-mail: hongchaoliu@sjtu.edu.cn

芮 智(1996—)，男，硕士研究生，研究方向为电力系统稳定性。E-mail: ruizhi1996@sjtu.edu.cn

(编辑 姜新丽)