交直流混合配电网多阶段随机优化调度模型

裴 蕾，卫志农，陈 胜，赵景涛，傅 强

交直流混合配电网多阶段随机优化调度模型

裴 蕾1，卫志农1，陈 胜1，赵景涛2，傅 强2

(1.河海大学能源与电气学院，江苏 南京 211100；2.国电南瑞科技股份有限公司，江苏 南京 211100)

高比例间歇性分布式光伏的接入给交直流混合配电网的运行带来了挑战。当前所提两阶段随机优化调度模型对不确定变量的观测较为粗略，导致配电网实时决策与日前决策偏差较大。鉴于此，提出了基于场景树的交直流混合配电网多阶段随机优化模型。所提模型以日前购电成本、日内调节成本和实时平衡成本之和最小为目标，通过储能装置的充放电功率调节、换流站输出功率调节和需求响应等灵活调节措施，实现了间歇性光伏的就地消纳和系统的削峰填谷。多阶段随机优化模型的日前离散决策变量可随日内和实时阶段的不确定信息改变而自适应调整，更符合实际高比例光伏渗透下交直流混合配电网的运行需求，为其经济灵活运行提供技术支撑。

交直流混合配电网；多阶段决策；随机优化；场景树；分布式光伏

0 引言

近年来，间歇性分布式光伏(Photovoltaic, PV)和储能装置(Energy Storage System, ESS)等直流电源大量并入配电网，配电网侧大功率电力电子设备技术快速发展，电动汽车(Electric Vehicle, EV)等直流荷的需求日益增加，传统交流配电网正演变为交直流混合配电网[1-2]。相比于传统交流配电网，交直流混合配电网传输容量更大，运行更为灵活，更有利于分布式光伏的接入[3-4]。当分布式光伏高比例渗透时，交直流混合配电网如何利用灵活性资源实现配电网的优化调度，减少配电网运行成本成为目前亟需解决的问题之一。

分布式光伏的接入、储能装置的控制和灵活负荷的需求响应使得交直流混合配电网的主动性更强，合理的优化调度策略可以保证配电网的安全经济运行。文献[5]提出了基于二阶锥松弛的日前交直流混合配电网确定性优化调度模型，考虑了分布式光伏、储能装置和分组电抗器的主动调节作用，实现了日前配电网运行成本的优化。但是间歇性分布式光伏出力具有很大的随机性，确定性优化调度模型的优化结果通常较为保守，建立计及光伏出力不确定性的随机优化调度模型更加符合实际情况。

描述光伏或风电出力等不确定因素的模型通常有随机规划模型、机会约束模型、鲁棒优化模型和分布鲁棒优化模型[6]。其中，随机规划模型通常基于概率理论采用场景的方法描述不确定信息或用服从一定概率分布的随机变量描述不确定因素，建立以期望成本最小为目标的随机模型[7]。机会约束模型采用随机变量的表达式描述不确定因素，最大特点为允许所做的决策在一定程度上不满足配电网运行约束条件[8]。鲁棒优化模型则通过构建不确定集合来对光伏和风电出力建模，该模型可以得到最恶劣场景下的优化方案，但是通常容易使得优化结果过于保守[9-10]。分布鲁棒优化模型结合了鲁棒优化模型和随机优化模型的优点，可得到随机变量最恶劣概率分布情况下的决策[11]。文献[12]考虑了新能源出力的波动区间，以期望场景的网损成本最小为目标，建立交直流混合配电网鲁棒优化模型。文献[13]采用场景削减技术生成相应概率的光伏出力场景和风电出力场景集合，生成了光伏出力和风电出力的典型场景。文献[14]采用样本均值近似方法将原机会约束规划模型转化为较易求解的确定性优化模型。文献[15]提出了以降低运行成本和控制无功电压为目标的交直流混合配电网二阶段鲁棒优化模型，该模型为双层规划模型，能够得到最恶劣新能源出力场景下运行成本最少的无功电压控制方案。文献[16]研究了两阶段主动配电网优化调度模型，日前阶段以配电网运行成本最低为目标，日内阶段根据新能源出力的预测误差进行滚动优化调整。文献[17]考虑微电网和配电网两个不同利益体，采用极端场景集描述不确定性因素，构建日内-实时两阶段随机规划模型。文献[18]对分布鲁棒优化方法在电力系统中的应用进行了综述，分析了不同类型分布鲁棒优化方法的优缺点。

值得注意的是，当前针对随机规划模型与鲁棒优化模型的研究主要侧重两阶段优化调度模型。文献[19]提出了考虑非预期约束条件的电力系统多阶段随机规划模型，发现多阶段随机规划可以得到更低的优化目标值，规划方法也更加灵活，但是仅应用于输电网规划问题中。两阶段优化调度模型通常分为日前和实时阶段，日前阶段决策变量不会随实时阶段不确定因素变化而调整，实时阶段可根据实时观察到的场景而进行优化调度策略的调整。然而，日前阶段对于光伏出力的观测精度十分有限，当日前阶段观测的光伏出力与实时阶段光伏的实际出力存在较大偏差时，不可避免地影响了光伏的消纳及配电网的安全经济运行。相比而言，在日内阶段光伏出力观测精度要明显高于日前阶段。因此，包括日前、日内和实时三个阶段的多阶段随机优化模型更值得研究。其中日前阶段离散决策变量可根据未来不确定信息的变化而进行调整；多阶段模型计及了日内调节阶段，一定程度上可避免日前新能源出力预测误差较大造成的实时阶段调节成本过高。最后，实际配电网优化调度问题中每一阶段观察到的不确定场景都可以影响之前的决策，但是当前阶段同一不确定场景下决策需保持一致性，因此需要增加非预期约束条件[20-21]。

综上所述，本文提出计及间歇性光伏不确定性的交直流混合配电网多阶段随机优化调度模型，采用储能装置的充放电功率调节、换流器输出功率调节和需求响应等灵活调节措施实现日前购电成本、日内调节成本和实时平衡成本最小化的目标。本文所提交直流混合配电网多阶段随机优化调度模型有望为配电网安全经济运行奠定基础。

1 交直流混合配电网二阶锥松弛模型

本节首先介绍了交流配电网和直流配电网的非线性潮流模型，其次对电压源换流器进行数学建模，最后进行变量替换，将原非凸潮流方程进行二阶锥松弛。

1.1 交流配电网潮流模型

采用Distflow支路模型[22]描述交流配电网多时段潮流模型：

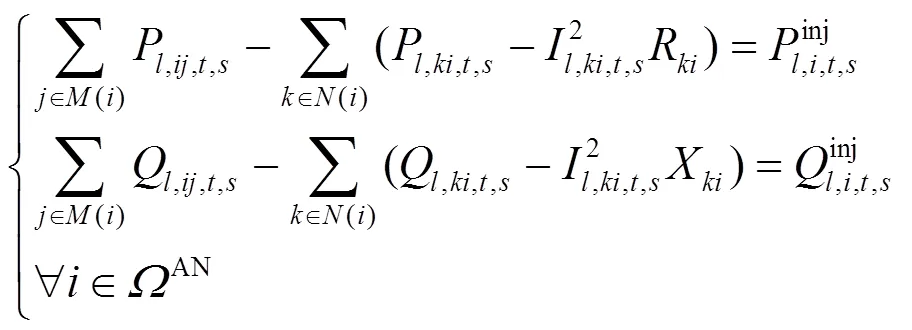
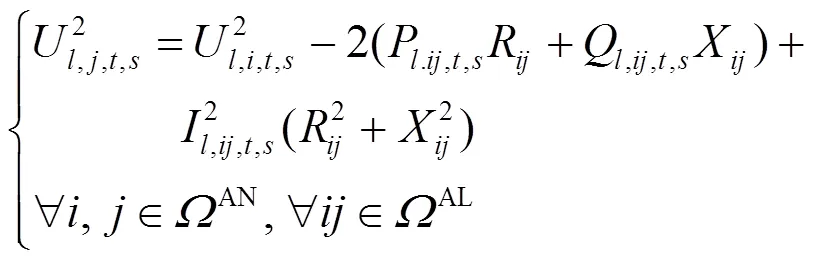
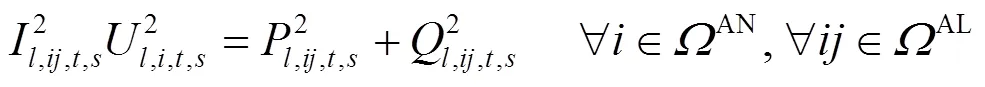
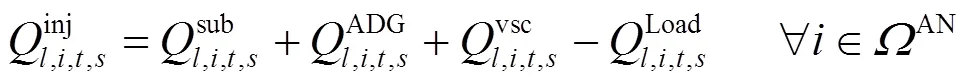
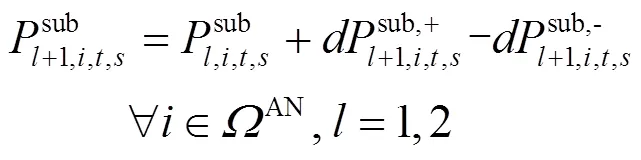
1.2 直流配电网潮流模型

根据交流电网支路潮流建模方法，可得到直流配电网多时段潮流模型。

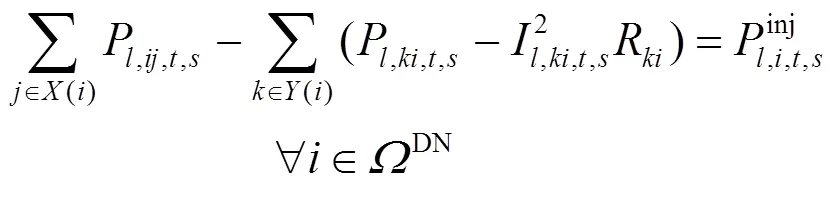
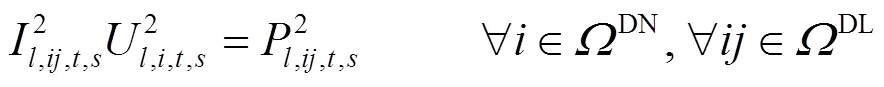
1.3 换流器建模

本文采用电压源换流器(Voltage Source Converter, VSC)单相模型，主要由等值阻抗和理想VSC组成，换流损耗由等值电阻消耗功率等效[23]。

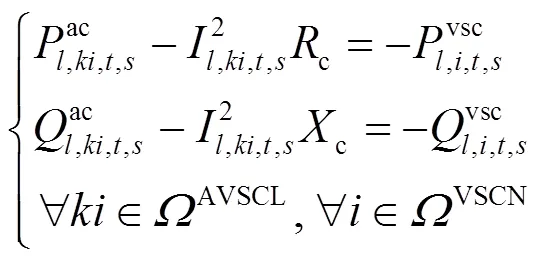
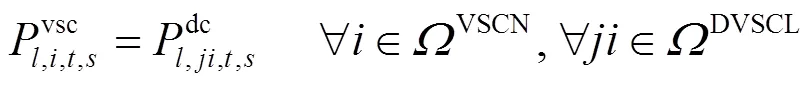
1.4 二阶锥松弛

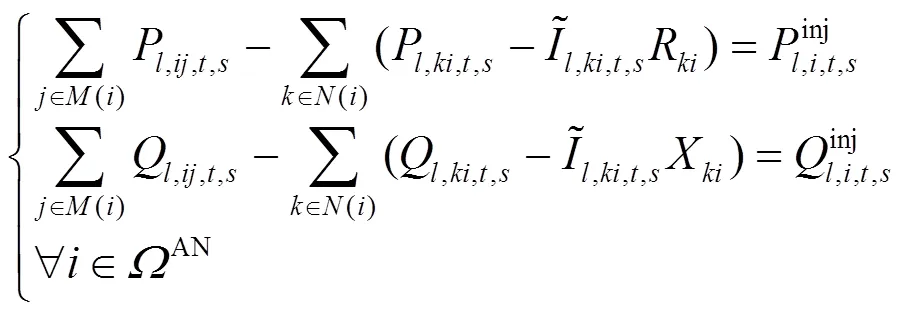
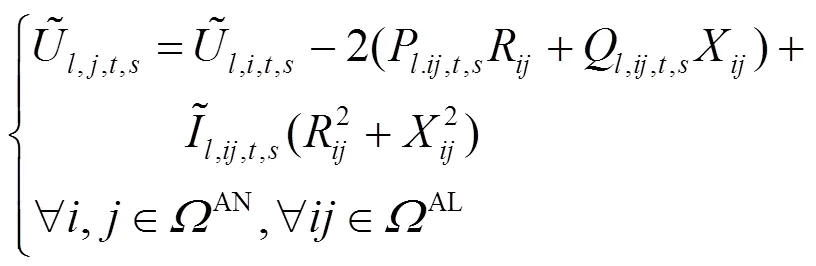
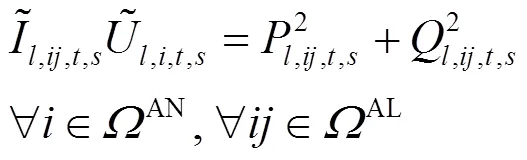
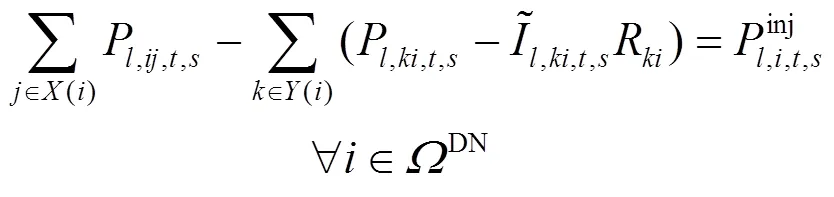
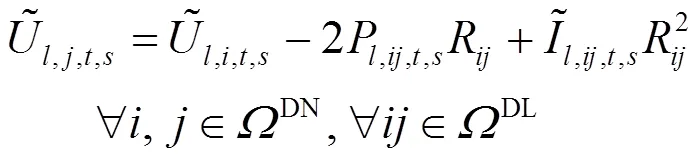
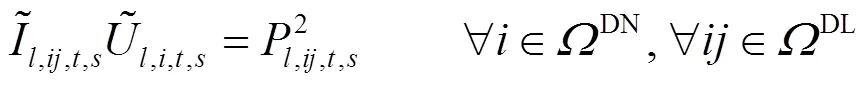
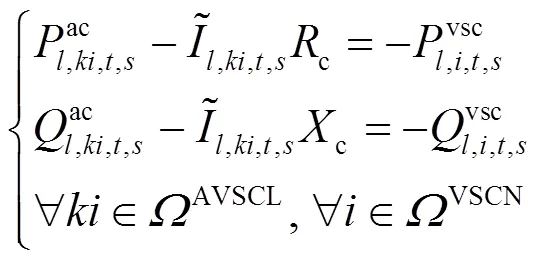
将式(15)和式(18)进行二阶锥松弛，得到

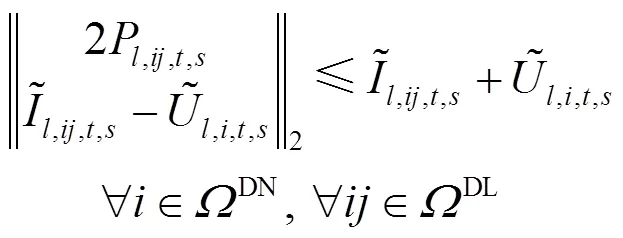
2 交直流混合配电网多阶段优化调度模型

由于日前、日内和实时阶段的光伏出力的观测值一般不一致，因此在各阶段运行决策中，配电网从主网的购电量会存在偏差。交直流混合配电网三阶段交易模式可简述为：在日内/实时阶段存在功率缺额时，可向主网高价购买额外的电量；而当日内/实时功率过剩时，可低价将多余的电量售出。

多阶段随机优化模型将配电网优化调度过程分为多个阶段，每阶段的决策变量可依据最新观测到的光伏的不确定性出力信息而调整，并且同一场景下的决策保持一致性，即当前的决策不应该依赖于未来的随机因素和决策量。

2.1 目标函数

目标函数由日前主网购电费用、日内调节费用、实时调节费用和实时需求响应补偿费用构成，如式(22)—式(25)所示。

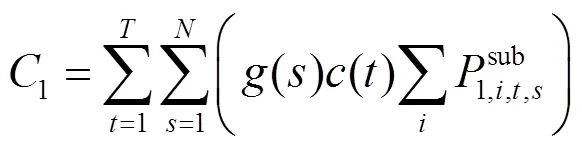
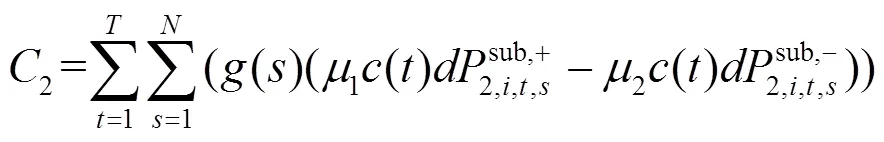
2.2 交直流混合配电网运行约束

交直流混合配电网潮流方程约束见式(1)—式(21)。

2.2.1交流配电网安全约束条件

交流配电网的运行需满足以下安全约束。

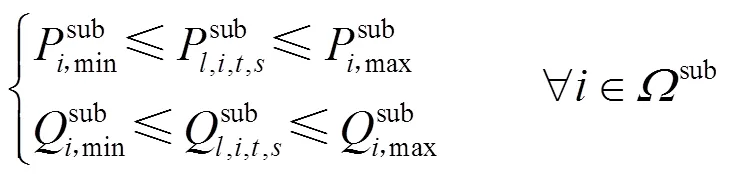
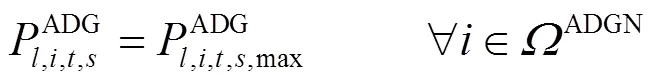
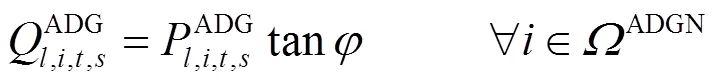
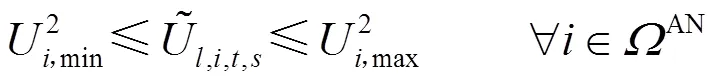
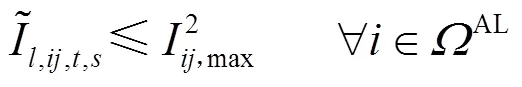
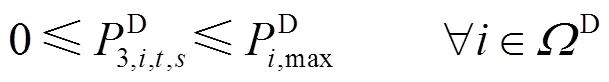
2.2.2直流配电网安全约束条件

直流配电网的运行需满足以下安全约束。

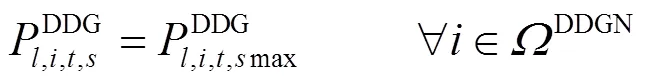
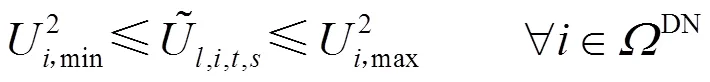
储能装置的充放电策略在日前阶段确定，并在日内阶段和实时阶段保持不变。储能装置运行约束包括充放电功率约束、充放电次数约束和储能电量约束[25]，如式(36)—式(40)所示。

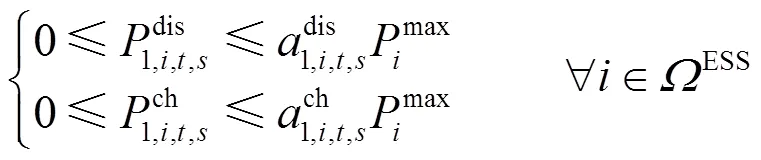
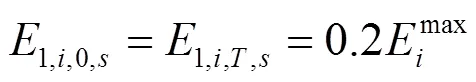
2.2.3换流器安全约束条件

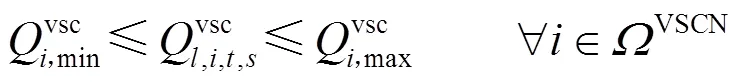
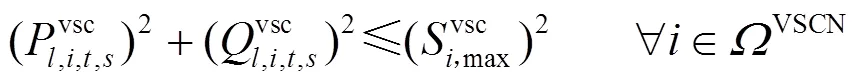
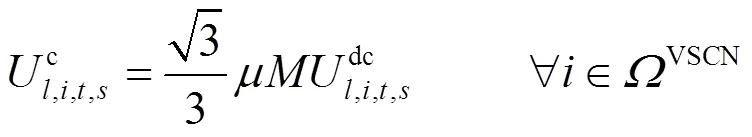
2.3 场景树的构建

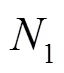
图1 场景树的构建

2.4 非预期约束条件

多阶段随机优化模型中含有非预期约束条件，决策变量可随着未来不确定因素的确定化过程不断调节，根据观察到的实时信息进行调整，但是当前决策只取决于当前所观察到的光伏出力场景，即当前阶段同一光伏出力场景下的决策需保持一致性[21]，如图2所示。

图2 非预期约束示意图

本文所提交直流混合配电网多阶段随机优化模型非预期约束条件如式(45)和式(46)所示。

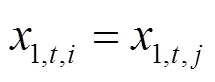
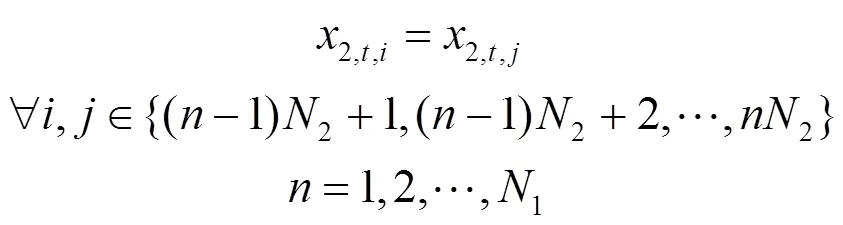
需要说明的是，所提模型为混合整数二阶锥规划(Mixed Integer Second-order Cone Programming, MISOCP)问题。

2.5 交直流混合配电网两阶段优化调度模型

传统两阶段优化模型只包括日前和实时两个阶段，数学模型如式(47)所示。

区别于多阶段随机优化模型，传统两阶段随机优化模型缺少日内调节阶段，第一阶段决策变量不随第二阶段不确定场景变化而调整，第二阶段决策变量可根据不确定场景实时变化而灵活调整[27]。

此处定义多阶段经济价值指标(Value of Multi- stage Operation, VMO)，VMO等于三阶段优化调度模型与两阶段优化调度模型运行总成本的百分比之差，该指标用于定量衡量所提多阶段随机优化模型相比于传统两阶段优化模型的经济价值。

3 算例分析

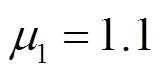
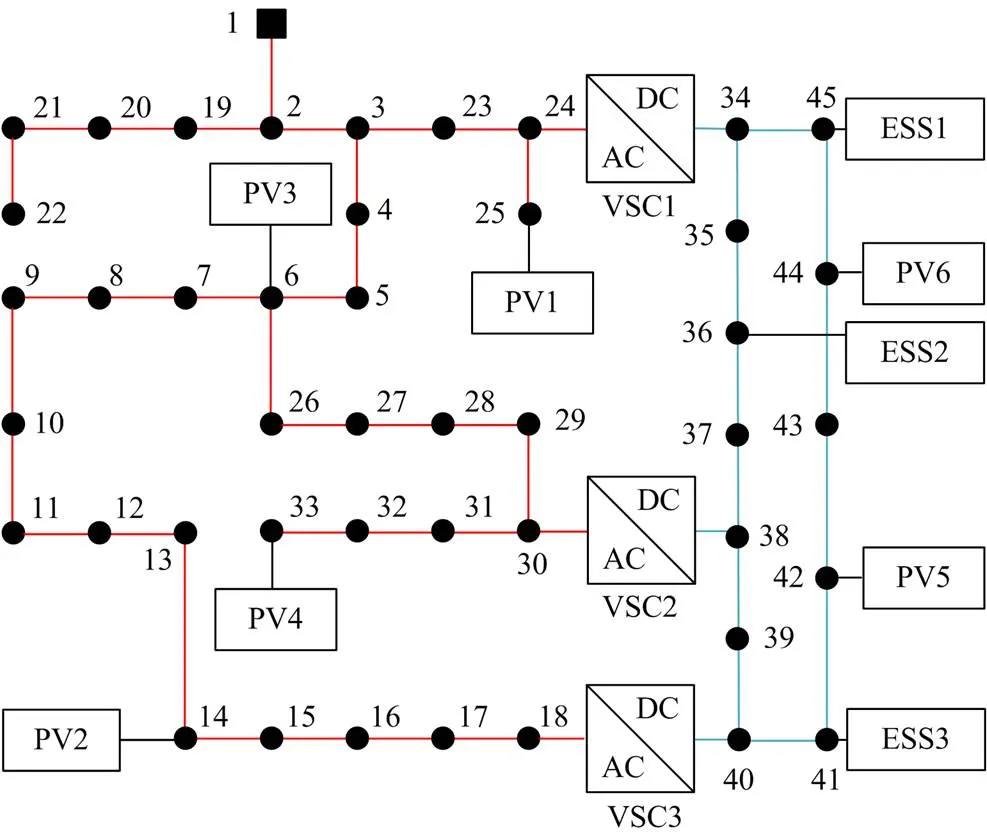
图3 修改的45节点测试系统拓扑图

3.1 储能装置的调节作用

储能装置的充放电策略在日前阶段确定，合理的ESS调度方案可缓解PV出力不确定性带给配电网的影响，起到削峰填谷的作用。本文得到了直流配电网中储能装置一天内的电量变化曲线，结果如图4所示。

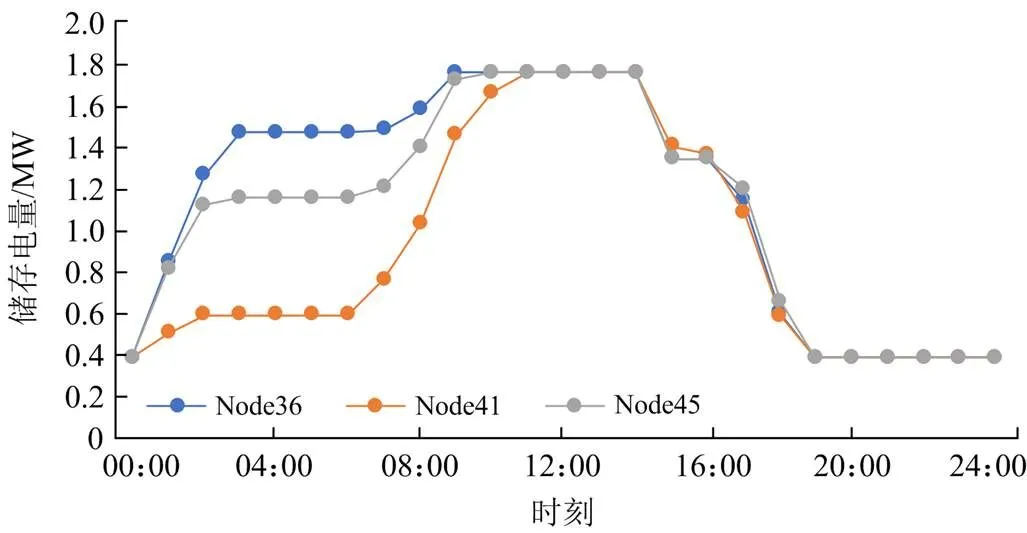
图4 ESS装置储存电量变化曲线

由图4可知：在00：00—03：00时段，负荷较少且电价较低，配电网向主网低价购电，ESS装置充电，储存电量上升；在07：00—10：00时段，负荷较重且电价较高，但是光伏机组出力较大，在满足负荷需求的同时对ESS装置充电，为下一阶段的放电过程做准备；在13：00—19：00时段，光照强度变弱，用电到达高峰期，ESS装置开始放电，以此达到减少主网购电成本的目的。同时，为保证下一个充放电周期正常进行，ESS装置恢复至原始荷电状态。

3.2 两阶段与多阶段调度的需求响应对比

交直流混合配电网较接近主动配电网，便于电动汽车充电桩等可直接中断负荷的接入。柔性负荷可实现配电网与用户间能量双向传递，通过合理的调度策略可达到促进光伏消纳、减少负荷峰谷差和降低主网购电成本等目的。

设定柔性负荷的需求响应仅发生在实时平衡阶段，图5和图6分别展示了在15个场景下两阶段和多阶段随机优化模型的柔性负荷响应量的需求响应量，两图表明在09：00—11：00和14：00用电高峰时段，实时阶段平衡成本较高，此时若配电网存在功率缺额，柔性负荷响应的补偿费用较低，则调度人员增加柔性负荷的响应量。

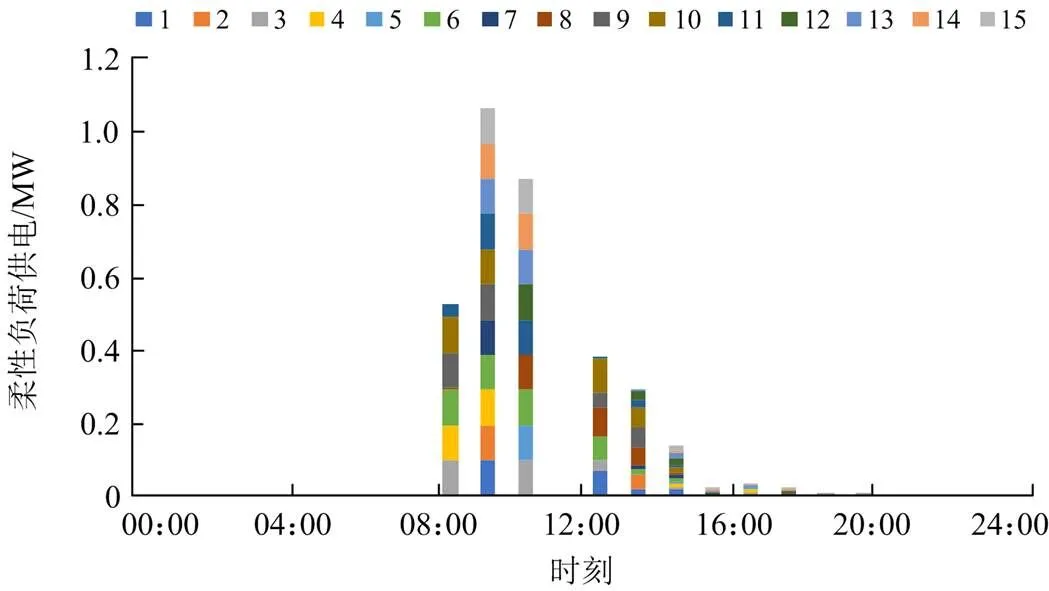
图5 两阶段随机优化模型的柔性负荷响应量

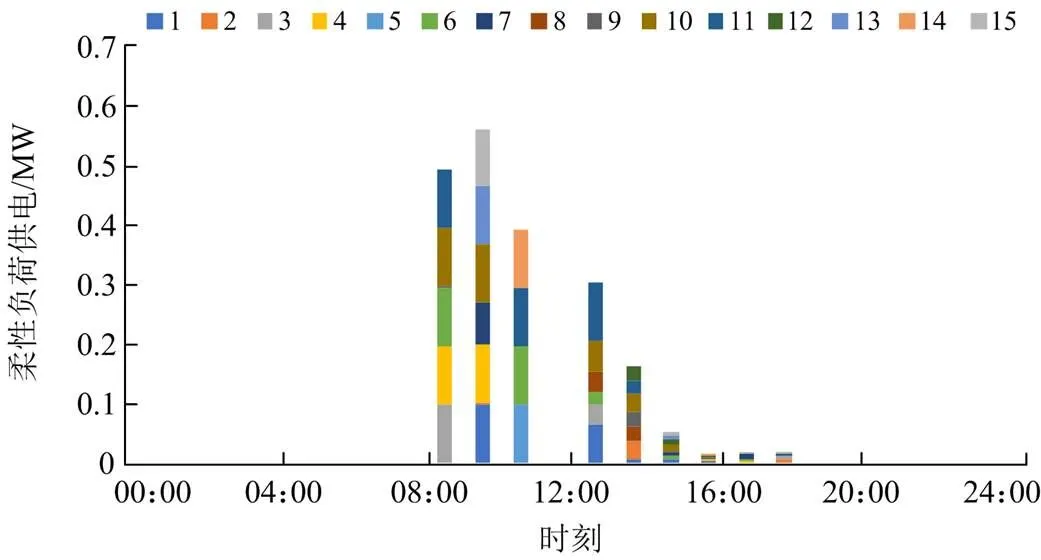
图6 多阶段随机优化模型的柔性负荷响应量

由于两阶段优化调度模型缺少日内调节环节，相比于多阶段优化调度模型，两阶段调度模型下柔性负荷的响应量更大，等价于增加了实时运行阶段的调整成本。

3.3 不同光伏出力场景下调节成本对比

光伏出力不同会导致日内和实时阶段的调节成本变化，假设日前、日内及实时阶段光伏出力仅分为高、中、低三种情况，不同阶段光伏出力情况不同，观察各阶段成本的变化，结果如表1所示。

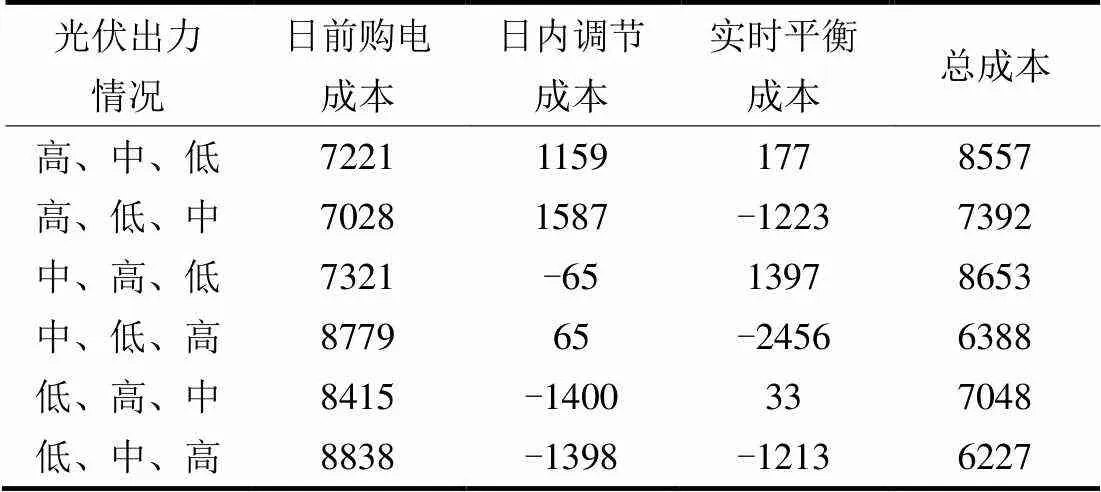
表1 各阶段不同光伏出力情况下调节成本对比

表1说明当光伏出力不足而无法满足负荷需求时，即日内/实时阶段存在功率缺额，可向主网高价购买额外的电量，此时调节成本为正。而当光伏出力冗余，日内/实时功率过剩时，可低价将多余的电量售出，调节成本则为负。此外，日前阶段的储能装置通过合理的充放电调度策略可实现电价较低时充电，电价较高时放电。因此，当日前阶段光伏出力较少无法满足08：00—12：00电价较高时段的负荷需求时，储能装置将在此时段放电。由于储能装置的充放电策略在日内和实时阶段保持不变，当日内和实时阶段光伏出力高于日前出力时，多余的光伏出力可向主网出售，且不存在柔性负荷调节成本，因此日前光伏出力较低的场景的总成本相对较低。

3.4 两阶段与三阶段调度的总成本对比

表2 两阶段与多阶段调度下总运行成本对比

本文提出的交直流混合配电网多阶段随机优化模型的原模型为混合整数非线性规划(Mixed Integer Nonlinear Programming, MINLP)模型，利用二阶锥松弛技术可将其转化MISOCP问题，表3为两种模型的求解结果比较。

表3 MINLP与MISOCP的求解结果对比

本文所提MISOCP模型的运行成本与MINLP模型一致，验证了MISOCP模型解的有效性(即二阶锥松弛的严格性)。此外，采用MISOCP模型的求解效率明显快于MINLP模型。

4 结语

间歇性分布式光伏的接入增加了交直流混合配电网的不确定性，合理的调度策略可以实现配电网的经济运行。本文提出了交直流混合配电网多阶段随机优化模型，基于算例结果可得出如下结论。

1) 合理的储能装置充放电策略可以起到消纳光伏出力和削峰填谷的作用，且能缓解光伏出力不确定性带给配电网的影响。

2) 相比于传统两阶段随机优化模型，多阶段随机优化模型的日前离散决策变量可随日内和实时阶段的不确定信息改变而自适应调整，因此更适用于高比例新能源渗透的交直流混合配电网。

3) 多阶段随机优化模型由于增加了日内调节环节使得实时阶段的平衡成本和需求响应的补偿费用大为降低，减少了交直流混合配电网的总运行成本。

附录

附表1 45节点算例结构数据

Attached Table 1 Data of 45-node test system

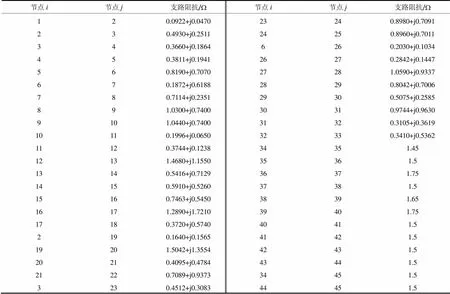
节点i节点j支路阻抗/W节点i节点j支路阻抗/W 120.0922+j0.047023240.8980+j0.7091 230.4930+j0.251124250.8960+j0.7011 340.3660+j0.18646260.2030+j0.1034 450.3811+j0.194126270.2842+j0.1447 560.8190+j0.707027281.0590+j0.9337 670.1872+j0.618828290.8042+j0.7006 780.7114+j0.235129300.5075+j0.2585 891.0300+j0.740030310.9744+j0.9630 9101.0440+j0.740031320.3105+j0.3619 10110.1996+j0.065032330.3410+j0.5362 11120.3744+j0.123834351.45 12131.4680+j1.155035361.5 13140.5416+j0.712936371.75 14150.5910+j0.526037381.5 15160.7463+j0.545038391.65 16171.2890+j1.721039401.75 17180.3720+j0.574040411.5 2190.1640+j0.156541421.5 19201.5042+j1.355442431.5 20210.4095+j0.478443441.5 21220.7089+j0.937334451.5 3230.4512+j0.308344451.5

附图1 有功负荷曲线

Attached Fig. 1 Active load curve

[1] 张福民, 刘国鑫, 李占凯, 等. 基于二阶锥规划的交直流混合配电网优化调度[J]. 智慧电力, 2020, 48(3): 117-123.

ZHANG Fumin, LIU Guoxin, LI Zhankai, et al. Optimal dispatch of AC/DC hybrid distribution network based on second-order cone programming[J]. Smart Power, 2020, 48(3): 117-123.

[2] 张璐, 唐巍, 卢莹, 等. 面向新型源荷接入的交直流混合配电网关键技术研究综述[J]. 供用电, 2020, 37(10): 3-9, 21.

ZHANG Lu, TANG Wei, LU Ying, et al. Overview of hybrid AC/DC distribution network key technologies facing novel source and load integration[J]. Distribution & Utilization, 2020, 37(10): 3-9, 21.

[3] 崔福博, 郭剑波, 荆平, 等. 直流配电技术综述[J]. 电网技术, 2014, 38(3): 556-564.

CUI Fubo, GUO Jianbo, JING Ping, et al. A review of DC power distribution technology[J]. Power System Technology, 2014, 38(3): 556-564.

[4] 曾嘉思, 徐习东, 赵宇明. 交直流配电网可靠性对比[J]. 电网技术, 2014, 38(9): 2582-2589.

ZENG Jiasi, XU Xidong, ZHAO Yuming. Reliability comparison of AC and DC distribution network[J]. Power System Technology, 2014, 38(9): 2582-2589.

[5] 马鑫, 郭瑞鹏, 王蕾, 等. 基于二阶锥规划的交直流主动配电网日前调度模型[J]. 电力系统自动化, 2018, 42(22): 144-150.

MA Xin, GUO Ruipeng, WANG Lei, et al. Day-ahead scheduling model for AC/DC active distribution network based on second-order cone programming[J]. Automation of Electric Power Systems, 2018, 42(22): 144-150.

[6] 胡代豪, 郭力, 刘一欣, 等. 计及光储快充一体站的配电网随机-鲁棒混合优化调度[J]. 电网技术, 2021, 45(2): 507-519.

HU Daihao, GUO Li, LIU Yixin, et al. Stochastic/robust hybrid optimal dispatching of distribution networks considering fast charging stations with photovoltaic and energy storage[J]. Power System Technology, 2021, 45(2): 507-519.

[7] 钱科军, 刘乙, 张新松, 等. 考虑电动汽车充电负荷的配电系统场景概率潮流分析[J]. 电力系统保护与控制, 2020, 48(24): 62-70.

QIAN Kejun, LIU Yi, ZHANG Xinsong, et al. Scenario- based probabilistic power flow calculation of distribution systems with electric vehicle charging loads[J]. Power System Protection and Control, 2020, 48(24): 62-70.

[8] LI Pan, JIN Baihong, WANG Dai, et al. Distribution system voltage control under uncertainties using tractable chance constraints[J]. IEEE Transactions on Power Systems, 2019, 34(6): 5208-5216.

[9] 蔡宇, 林今, 万灿, 等. 市场环境下基于随机规划的主动配电网运行交易二层优化模型[J]. 中国电机工程学报, 2016, 36(20): 5391-5402.

CAI Yu, LIN Jin, WAN Can, et al. A bi-level stochastic programming approach for strategic active distribution network operation in electricity market[J]. Proceedings of the CSEE, 2016, 36(20): 5391-5402.

[10] CHEN Sheng, WEI Zhinong, SUN Guoqiang, et al. Adaptive robust day-ahead dispatch for urban energy systems[J]. IEEE Transactions on Industrial Electronics, 2019, 66(2): 1379-1390.

[11] 陈泽雄, 张新民, 王雪锋, 等. 分布式光伏电站接入配电网的分布鲁棒优化配置方法[J]. 电力系统保护与控制, 2021, 49(13): 30-42.

CHEN Zexiong, ZHANG Xinmin, WANG Xuefeng, et al. A distributionally robust optimal allocation method for distributed photovoltaic generation stations integrated into a distribution network[J]. Power System Protection and Control, 2021, 49(13): 30-42.

[12] 孙峰洲, 刘海涛, 陈庆, 等. 考虑新能源波动区间的交直流配电网下垂斜率鲁棒优化方法[J]. 电力系统自动化, 2020, 44(14): 62-70.

SUN Fengzhou, LIU Haitao, CHEN Qing, et al. Robust optimization method for droop slopes in AC/DC distribution network considering fluctuation interval of renewable energy source[J]. Automation of Electric Power Systems, 2020, 44(14): 62-70.

[13] 白斌, 韩明亮, 林江, 等. 含风电和光伏的可再生能源场景削减方法[J]. 电力系统保护与控制, 2021, 49(15): 141-149.

BAI Bin, HAN Mingliang, LIN Jiang, et al. Scenario reduction method of renewable energy including wind power and photovoltaic[J]. Power System Protection and Control, 2021, 49(15): 141-149.

[14] 许寅, 李佳旭, 王颖, 等. 考虑光伏出力不确定性的园区配电网日前运行计划[J]. 电力自动化设备, 2020, 40(5): 85-91, 105.

XU Yin, LI Jiaxu, WANG Ying, et al. Day-ahead operation plan for campus distribution network considering uncertainty of photovoltaic output[J]. Electric Power Automation Equipment, 2020, 40(5): 85-91, 105.

[15] 符杨, 张智泉, 李振坤, 等. 基于二阶段鲁棒博弈模型的微电网群及混合交直流配电系统协调能量管理策略研究[J]. 中国电机工程学报, 2020, 40(4): 1226-1240.

FU Yang, ZHANG Zhiquan, LI Zhenkun, et al. A two-stage robust game approach for coordinated energy management in hybrid AC/DC distribution system with microgrid clusters[J]. Proceedings of the CSEE, 2020, 40(4): 1226-1240.

[16] 刘一欣, 郭力, 王成山. 微电网两阶段鲁棒优化经济调度方法[J]. 中国电机工程学报, 2018, 38(14): 4013-4022.

LIU Yixin, GUO Li, WANG Chengshan. Economic dispatch of microgrid based on two stage robust optimization[J]. Proceedings of the CSEE, 2018, 38(14): 4013-4022.

[17] 黄张浩, 张亚超, 郑峰, 等. 基于不同利益主体协调优化的主动配电网日前-实时能量管理方法[J]. 电网技术, 2021, 45(6): 2299-2308.

HUANG Zhanghao, ZHANG Yachao, ZHENG Feng, et al. Day-ahead and real-time energy management method for active distribution networks based on coordinated optimization of different stakeholders[J]. Power System Technology, 2021, 45(6): 2299-2308.

[18] 贺帅佳, 阮贺彬, 高红均, 等. 分布鲁棒优化方法在电力系统中的理论分析与应用综述[J]. 电力系统自动化, 2020, 44(14): 179-191.

HE Shuaijia, RUAN Hebin, GAO Hongjun, et al. Overview on theory analysis and application of distributionally robust optimization method in power system[J]. Automation of Electric Power Systems, 2020, 44(14): 179-191.

[19] 丁涛, 李澄, 胡源, 等. 考虑非预期条件的电力系统多阶段随机规划建模理论与方法[J]. 电网技术, 2017, 41(11): 3566-3572.

DING Tao, LI Cheng, HU Yuan, et al. Multi-stage stochastic programming for power system planning considering nonanticipative constraints[J]. Power System Technology, 2017, 41(11): 3566-3572.

[20] DING T, HU Y, BIE Z. Multi-stage stochastic programming with nonanticipativity constraints for expansion of combined power and natural gas systems[J]. IEEE Transactions on Power Systems, 2018, 33(1): 317-328.

[21] ABBASPOURTORBATI F, CONEJO A J, WANG J, et al. Three-or two-stage stochastic market-clearing algorithm?[J]. IEEE Transactions on Power Systems, 2017, 32(4): 3099-3110.

[22] 刘一兵, 吴文传, 张伯明, 等. 基于混合整数二阶锥规划的主动配电网有功-无功协调多时段优化运行[J]. 中国电机工程学报, 2014, 34(16): 2575-2583.

LIU Yibing, WU Wenchuan, ZHANG Boming, et al. A mixed integer second-order cone programming based active and reactive power coordinated multi-period optimization for active distribution network[J]. Proceedings of the CSEE, 2014, 34(16): 2575-2583.

[23] 王守相, 陈思佳, 谢颂果. 考虑安全约束的交直流配电网储能与换流站协调经济调度[J]. 电力系统自动化, 2017, 41(11): 85-91.

WANG Shouxiang, CHEN Sijia, XIE Songguo. Security- constrained coordinated economic dispatch of energy storage systems and converter stations for AC/DC distribution networks[J]. Automation of Electric Power Systems, 2017, 41(11): 85-91.

[24] SHANG L, GUO H, ZHU W. An improved MPPT control strategy based on incremental conductance algorithm[J]. Protection and Control of Modern Power Systems, 2020, 5(2): 66-73.

[25] 陈长青, 阳同光. 计及柔性负荷的电网储能和光伏协调规划研究[J]. 电力系统保护与控制, 2021, 49(4): 169-177.

CHEN Changqing, YANG Tongguang. Research on grid energy storage and photovoltaic coordination planning with flexible load[J]. Power System Protection and Control, 2021, 49(4): 169-177.

[26] 郑超,周孝信,李若梅,等.VSC-HVDC稳态特性与潮流算法的研究[J]. 中国电机工程学报, 2005, 25(6): 1-5.

ZHENG Chao, ZHOU Xiaoxin, LI Ruomei, et al. Study on the steady characteristic and algorithm of power flow for VSC-HVDC[J]. Proceedings of the CSEE, 2005, 25(6): 1-5.

[27] 庄慧敏, 肖建. 主动配电网的两阶段优化调度模型[J]. 西南交通大学学报, 2015, 50(5): 928-934.

ZHUANG Huimin, XIAO Jian. Two-stage optimal schedule model for active distribution network[J]. Journal of Southwest Jiaotong University, 2015, 50(5): 928-934.

[28] 马鑫, 郭瑞鹏, 柳劲松, 等. 三相不平衡下交直流配电网状态估计[J]. 电力系统自动化, 2019, 43(23): 65-71.

MA Xin, GUO Ruipeng, LIU Jinsong, et al. State estimation for three-phase unbalanced AC/DC distribution network[J]. Automation of Electric Power Systems, 2019, 43(23): 65-71.

Multi-stage stochastic optimization dispatch model for AC-DC hybrid distribution power networks

PEI Lei1, WEI Zhinong1, CHEN Sheng1, ZHAO Jingtao2, FU Qiang2

(1. College of Energy and Electrical Engineering, Hohai University, Nanjing 211100, China;2. NARI Technology Company Limited, Nanjing 211100, China)

The high proportion of intermittent distributed photovoltaic access brings challenges to the operation of an AC-DC hybrid distribution network. The current two-stage stochastic optimization dispatch model leads to a large deviation between real-time and day-ahead decision-making. This paper presents a multi-stage stochastic optimization model based on a scenario tree. The proposed model aims at minimizing the sum of day-ahead purchase cost, day-ahead adjustment cost and real-time balance cost. The model also realizes photovoltaic absorption and peak load filling through flexible adjustment measures such as energy storage device adjustment, converter station output power adjustment and demand response. The discrete decision variables of the multi-stage stochastic optimization model can be adjusted adaptively with the change of uncertain information in the intra-day and real-time stage. This can meet the operational requirements of an AC-DC hybrid distribution network with a high proportion of PV penetration and provide technical support for its economical and flexible operation.

AC-DC hybrid distribution network; multi-stage decision-making; stochastic optimization; scenario tree; distributed PV

10.19783/j.cnki.pspc.211212

国家自然科学基金项目资助 (U1966205)

This work is supported by the National Natural Science Foundation of China (No. U1966205).

2021-09-01；

2021-12-24

裴 蕾(1996—)，女，硕士研究生，主要研究方向为交直流混合配电网运行与控制；E-mail: 2474533628@qq.com

卫志农(1962—)，男，通信作者，博士，教授，主要研究方向为配电网态势感知与优化运行；E-mail: wzn_nj@ 263.net

陈 胜(1990—)，男，博士，副教授，主要研究方向为市场环境下的综合能源系统规划与运行。E-mail: chenshenghhu@163.com

(编辑 姜新丽)