在习题模型建构及运用中发展学生核心素养

鹿传旺

（山东省淄博第一中学，山东 淄博 255200）

笔者在求解折射率的习题课教学中，引领学生通过建构习题模型，并运用习题模型拓宽测定透明液体和固体折射率的实验设计思路.这样实现了学生从解决一个问题到解决一类问题，有效地减轻了学生的学业负担.［1］在习题模型建构和运用的过程中，［2］学生在诸如迁移、分析、推理、质疑、探究、创新等物理学科核心素养的诸多元素方面得到了较好的发展.

1 习题模型建构

例题.如图1 所示，一储油圆桶，底面直径与桶高均为d.当桶内无油时，从某点A 恰能看到桶底边缘上的某点B.当桶内油的深度等于桶高一半时，在A 点沿AB 方向看去，看到桶底上的C 点，C、B 相距d／4.求油的折射率为多少？

图1

1.1 光路模型建构

如图2所示，借助题干信息“当桶内无油时，从某点A 恰能看到桶底边缘上的某点B”构建折射光线的方向（AB 连线），综合信息“桶内油的深度等于桶高一半时，”AB 连线与油面交点确定入射点O，“在A 点沿AB 方向看去，看到桶底上的C 点，”构建出入射光线CO.入射角为i，折射角为α.

图2 光路模型图

1.2 数学模型建构

此为该习题模型折射率的数学模型.

在桶高、底面直径不变的情况下，桶内液面高低变化影响着O 点、C 点的位置.这些变化只是光路模型中OB、OC、BC、BD 对应线段的长度数值发生变化，其数学模型表征相同.若桶高、底面直径发生变化，会影响着O 点、C 点的位置，但其数学模型表征仍相同.

2 习题模型运用

2.1 透明液体折射率测定

如果桶里注入的是水，光线在水与空气界面处也会发生折射，会有同样现象发生，只不过C 点的具体位置有所变化.这点差异正好说明水不同于油，因此，可迁移至水的折射率的测定.如果再换成其他透明液体，其折射率也可测定.（核心素养提点：学生对知识、方法的迁移运用.）

图3

本实验相对于例题做了少许变动：一是使水面与桶口齐平.这样使折射点O 移至桶边缘E点，便于较精确操作.同时，C 点会离B 点较远些，测量时引起的误差相对较小.而倒入一半水时，折射点在中间，实验时不能精确控制，也会因C 点离B 较近，测量时引起的误差相对较大；二是在桶底放了一把尺，这样便能直接读出BC 的长度xC.（核心素养提点：学生对创新实验方案的分析论证.）

若把尺子立起来紧贴桶侧壁竖直放置，还能用该模型来测定水的折射率吗？答案是肯定的.

光路模型如图4所示，只需改变观察点A，沿着AO 方向（O 为桶上边缘E 点）观察，在尺子上C 位置处看到桶底B 点刻度值，同时在C 位置观察到尺子上方C′点的刻度值，光线OA 为光线C′O 的反射光线，同时也是光线BO 的折射光线，C 与C′关于D 点对称.据折射定律和几何关系，液体折射率的数学表征为

图4

需读出B、D、C′3点对应尺子的刻度值，算出BD间、CD 间长度，测出桶的直径DO，即可测出水的折射率.（核心素养提点：学生对实验方案的再创新意识和能力.）

光路模型构建中需要借助C′点的像C 确定折射光线OA，从而确定桶底边缘B 位置的观察位置在竖直方向上的C 点，原模型中桶底边缘B位置的观察位置在桶底上的C 点.共同点都是借助桶底边缘B 点构建光路模型，将入射角和折射角转化为两个直角三角形的内角，其正弦分别用三角形的边长表示，其数学原理相同.只是后来模型中两直角三角形有共同对直角边DO，原模型有共同邻直角边DO，数学模型表达式略有差异.（核心素养提点：学生对再创新实验方案的分析论证.）

批判质疑：如果仅仅是解决理想化的问题，“将水面与桶口齐平，使折射点O 移至桶边缘E点，”确实方便测量好操作.现实中水与桶边沿会因浸润现象和表面张力作用形成弯液面，导致折射光线方向发生变化，在实际测量中会带来较大误差.（核心素养提点：学生理论联系实际产生的对实验方案的批判和质疑.）

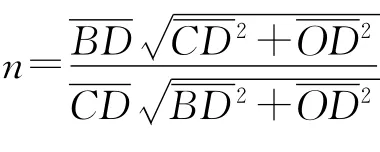
2.2 透明固体折射率测定

如果桶里注入的水结冰了，能否用上述构建的模型来测定冰的折射率呢？答案是肯定的.（核心素养提点：学生对所建模型的进一步迁移运用）

以图5对应的方式来看，水变成冰后，C 的位置读数发生变化，入射角、折射角的正弦值仍然用前面模型对应的三角形边长表示出来，求解折射率的数学模型形式不变.

图5

因冰是固体，不需要用桶去盛装，可直接用所建模型求解冰块的折射率.冰块的形状也不一定是柱状（桶的形状），可以是长方体、三棱柱等形状.因此，可以把构建的模型进一步迁移至测量其他透明固体的折射率，下面介绍用所建模型测定玻璃三棱镜的折射率.

为方便测量，使用等腰直角玻璃三棱镜.把三棱镜立在水平的纸面上，让其中的一个直角边的侧面与纸面接触，如图6 所示.眼从较远处（1 m外）［3］进行观察，让视线与AB 侧面平行，从AD 侧面中观察棱B 的虚像，视线与BD 交于C，保持眼睛的位置不动，在与三棱镜侧面接触的纸上做标记C，使它与棱B 的虚像看起来在一条直线上，再在纸上标出棱B 和D 的位置，只需测出BD、CD，因是等腰直角棱镜，OD等于CD.数学表征仍然是

图6 玻璃三棱镜中的光路图

对于非等腰直角棱镜，OD 的值一般不等于CD，需要进行测量.其他形状也可通过构建类似光路模型求出折射率，请读者自行拓展.

3 结束语

运用构建的模型解题是事半功倍的.通过构建习题模型实现从解决一个问题到解决一类问题，提高学习效率.习题教学作为物理教学中的重要组成部分，其对发展学生核心素养的作用非常大.教学实践中如何挖掘物理教学内容中蕴含的物理核心素养元素，将其渗透到平时的教学中，是落实新课标要求的关键.在日常的教学中，教师要善于根据不同题目的具体特点，通过提取信息、建构模型、迁移运用、分析解释、质疑评价等步骤，［4］引领学生运用模型实现从解题到解决问题.学生的眼界打开了、思维能力提升了，作业负担必然减轻.