化“变”为“定” 寻找极值条件
——对一道竞赛题的深入探析
2022-08-05高振
高 振
(山东省平邑县教育和体育局教研室,山东 临沂 273300)
1 原题再现
例题.(2019年第36届全国中学生物理竞赛山西赛区预赛第11 题)有一宽为l、高为2l的墙壁,如图1所示.现从墙壁左侧地面发射一个质量为m 的小球(可视为质点),使小球越过墙壁,击中墙壁右侧地面上的目标S.目标S 与墙壁中心线的距离为d.不计空气阻力.
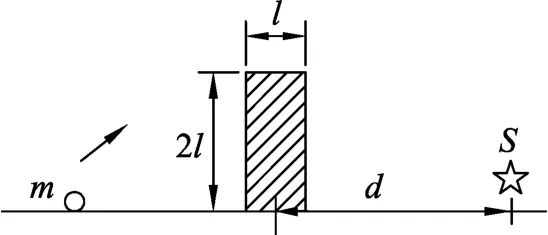
图1 题目图示
(1)小球有最小动能时,发射点与墙壁中心线的距离为多少?小球能够击中S 的最小初始速度与地面的夹角θ 为多少?
(2)若不需击中S,仅要求小球能够越过墙壁,求小球发射的最小动能,以及初始动能最小时发射点与墙壁中心线的距离为多少?
参考答案和许多师生在解答该题时,都未作分析论证直接认定(极值条件):击中目标或不需击中目标时,由于要求初动能最小,此时抛物线应该恰好过墙壁的两个角.两问均以上述极值条件作为解题的出发点,计算的结果为(计算过程略)
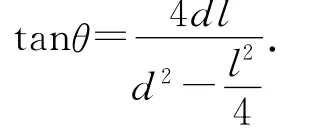

点评:该题以学生熟悉的抛体运动为背景,附加了小球越过墙壁的限制条件后,又在两小问中分别附加了需要击中目标或不需击中目标的限制条件,并提出了小球初动能最小(又一限制条件)的极值问题.在熟悉的抛体运动中添加多种“佐料”(3个维度的限制条件),这样巧妙地设计题目,使得原本师生以为熟悉而又平淡的抛体问题,变得极具趣味性和挑战性.体现了命题人高超的命题技巧和独具匠心的问题设计能力,是一道难得的好题.
由于该题以小球越过墙壁、击中或不击中目标、初动能最小等3个维度的限定下,要求考生分析求解极值问题.由于题目变化的因素多,寻找小球初动能最小的极值条件成了该题的难点,普遍反映该题难度大.
俗话说“好马要配好鞍子”,一道设计精巧的高难度好题,好比是一匹宝马,更需科学合理的解答,才算得上是“好马要配好鞍子”“锦上添花”.下面对该题难点——两小问中小球初动能最小的极值条件,分别做严密的分析论证.
2 分析论证两小问中小球初动能最小的极值条件
对于这样复杂多变(指题目中变化的因素)的物理问题,巧妙地应用物理学思想方法,从不同的视角去思考,找到恰当的途径,化“变”为“定”,减少问题中的变化因素,使问题变得简单明朗,才能顺利实现突破该题难点,找到小球初动能最小的极值条件的突破口.
2.1 用转化法化“变”为“定”,寻找不需击中目标时小球初动能最小的极值条件
当不需击中目标时,学生往往从地面上小球的发射点观察,发射点离墙壁的距离是变化的,发射速度方向与地面的夹角是变化的,同时还要满足小球越过墙壁这一限制条件.这样诸多的变化因素中,小球初速度最小的极值条件并不是显而易见的.
要减少上述诸多的变化因素,就要化“变”为“定”,就要应用转化法转化观察的视角,引导学生从与墙壁等高的水平面上观察(换角度思考),则容易看出小球越过墙壁的任意一条抛物线与墙壁等高的水平面的交点P、M 在墙角B、C 两点连线的外侧区域里(包括B、C 两点),如图2所示.
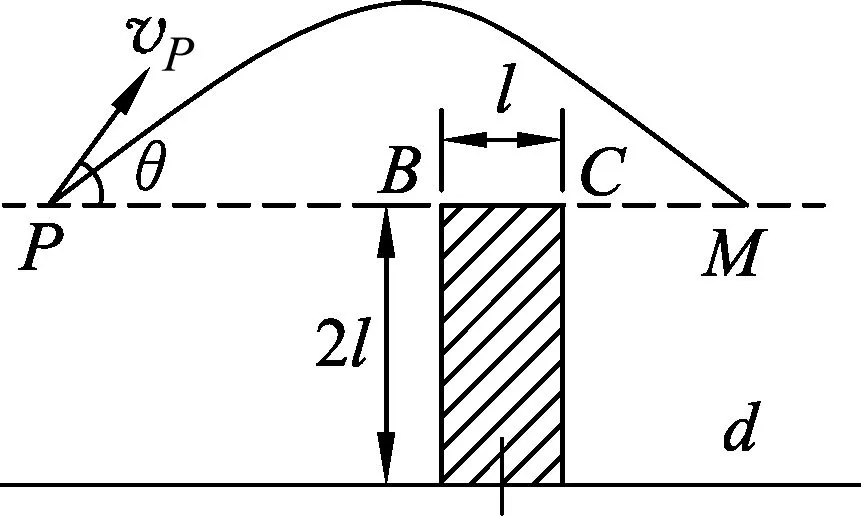
图2 与墙壁等高的水平面上观察
显然,只要P 点到M 点的距离xPM(变化)不小于墙壁宽度l(确定),小球一定能越过墙壁,则小球越过墙壁的条件为

由于不需击中目标,则小球发射点到墙壁中心线的距离x 可以由近及远地变化,使得小球在P 点的速度方向连续变化,即P、M 两点(由于等高,关于抛物线对称轴对称)的速度方向与水平面的夹角θ满足
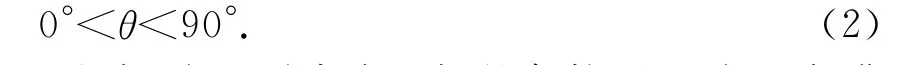
(注意:在不需击中目标的条件下,理解θ角满足(2)式是很重要的!)
设P 点的速度大小为vP,P 点到M 点的运动时间为t.则水平方向

由(1)、(2)、(5)式可知:当取xPM=l 最小值(此时P、M 点分别与B、C 点重合,抛物线的对称轴就是墙壁宽度l的中垂线),且取sin2θ=1最大值(此时θ=45°)时,vP有最小值,即小球在墙角B点速度的最小值为

当小球在B 点的速度最小时,由机械能守恒可知小球在发射点的速度也最小.
上述分析论证表明:不需击中目标时,参考答案第(2)问中的极值条件“要求初动能最小,此时抛物线应该恰好过墙壁的两个角”是正确的.
关于该题第(2)问的教学,笔者不主张凭物理直觉猜想得到上述极值条件,应该把教学的重点放在引导学生应用科学思维方法,进行严密的分析论证,从而找到发射小球初速度最小的极值条件.这样,不仅能有效地训练学生思维的灵活性、深刻性以及应用数学知识解决物理问题的能力,还能顺利地想到下面的不同于参考答案和文献[1]的更加突出物理本质的求解思路.

(8)式、(11)式分别与参考答案中的(3)式、(4)式相同,也与文献[2]3种解法的结果一致,殊途同归.
2.2 用逆向思维化“变”为“定”,寻找需要击中目标时小球初动能最小的极值条件
当需要击中目标时,受思维定势的影响,学生仍然会在与墙壁等高的水平面上观察.可是,在需要击中目标的条件制约,图2中小球在P 点的速度方向不再连续变化,即P、M 两点的速度方向与水平面的夹角θ 已经不满足(2)式了,因此无法用(5)式得出小球初动能最小的极值条件.已有的旧方法在第(1)问中失灵了,应该另辟蹊径,寻找第(1)问需要击中目标的限定条件下小球初动能最小的极值条件.
第(1)问中小球越过墙壁并击中目标的过程中,小球的发射点的位置在变化,发射点到墙壁中心线的距离也在变化.但是,若应用逆向思维,从击中的目标S 出发逆向观察,可以达到化“变”为“定”的目的,即目标S 到墙壁两侧面的距离都确定,如图3所示.从击中的目标S 出发逆向的运动中,很方便的定量表达小球越过墙壁的条件.

图3 发射小球击中目标的逆过程
根据抛物线的对称性,A 和S 两点的速度大小相等为v0,与地面的夹角θ也相等,设小球从S到C′和从S 到B′的运动时间分别为t1、t2.
要使小球越过墙壁(逆向运动已保证了“击中目标”),必须使抛物线上B′、C′两点的纵坐标yB′≥2l、且yC′≥2l.竖直方向小球做匀减速直线运动,则小球越过墙壁的条件为

至此,细心的读者可能已经看出了参考答案中第(1)问的极值条件是错误的.因为参考答案第(1)问在需要击中目标时,直接认定“由于要求初动能最小,此时抛物线应该恰好过墙壁的两个角.”这相当于在图3中直接认定B′、C′两点分别与B、C 两点重合,也相当于把不等式(12)、(13)式当成了等式,然后由(12)—(15)式4个方程直接 消 去v0、θ、t1、t24 个 未 知 量 中 的3 个 解 得 第4个未知量,并没有对初速度平方v02做数学极值分析.
下面由(12)、(13)式2个不等式,当θ取何值时,初速度平方v02取最小值,做严密的数学极值分析.
将(14)、(15)式中的时间分别代入(12)、(13)式,并两式相加整理得


把(19)、(20)式 代 入(25)式 所 得 结 果(表达式很繁,这里未写出,读者可验证)与参考答案中的x=d 不同.这又表明:需要击中目标时,参考答案中的极值条件“由于要求初动能最小,此时抛物线应该恰好过墙壁的两个角”是错误 的.[1]
