大数据分析技术在高校教育成本核算中的应用
2022-08-05宾扬帆
宾扬帆
(湖南环境生物职业技术学院,湖南 衡阳 421005)
0 引言
自从我国全面建成小康社会以来,不仅在经济建设上取得了巨大的成果,还将高校教育提上了改革计划的日程。高校教育的目的就是培养出源源不断的人才,为建设国家和服务社会提供人力资源。
目前我国高校教育中缺乏系统的资源管理,高校核算教育成本时通常采用较为粗糙的计算方法。这就导致核算值与实际应用值存在较大差别,使资源分配不均匀、资源浪费的情况时常发生。虽然在高校教育中投入了很多资源,但是效果却不尽人意。高校教育成本核算方法成了研究的热门话题。
随着经济的不断发展,科学技术也在不断创新发展。其中计算机科学的发展成果尤其显著。计算机科学中的大数据分析技术被广泛运用到生活中。大数据具有信息多样性、能够快速分析计算且数据库规模较大的特点。大数据分析与信息融合技术的应用为人们的工作和生活带来了很大的便利。
该文在此基础上提出了大数据分析技术在高校教育成本核算中的应用。利用大数据技术优化高校教育成本核算方法,设计出更加科学合理的核算方法,以提高核算精确度,为高校管理者提供精准信息,为高校教育的管理提供依据。
1 基于大数据分析技术的高校教育成本核算设计
1.1 基于大数据技术的高校教育成本数据处理
在建模前要对所收集的高校教育成本数据文件信息进行预先处理,筛选出条件稳定的数据作为建模的基础数据后再进行建模。具体的建模步骤如下。1)挑选数据试验集合和练习集合。通常用于建模的数据分为2个不同的类型:第1种是对模型进行练习的数据集合,模型能够在这个类型的数据集合中通过不断学习优化出最适合的数据,并抓取数据中有用的信息进行标记,同时学习数据行为,将信息的输入和输出行为进行优化,构建相对稳定的行为习惯,再通过学习与带有问题的数据进行对比,对整体数据库的性能进行优化操作。第2种数据是试验集合,当模型通过学习完成自我优化后,经过该数据集合能够对模型的数据全面性进行优化。所以,采集数据时要关注这2种数据集合的样本质量和个数。该文对模型进行设计时使用试错的方法对第1种数据集合进行设置,利用对2种数据集合的设置使建模数据更加完整,强化了模型性能。2)对所采集的基本数据进行归一化操作。对所采集的基本数据进行预处理在构建模型的前期准备中是十分重要的一步。由于基本数据是从不同的高校采集来的,所以数据的范围和标准也不同,倘若直接将这些收集来的基本数据用于构建模型,会因为标准和数据范围的不同而使模型在核算成本时不稳定,不能准确公平地进行成本核算。因此建模时要先进行预处理,将数据进行归一化操作,统一数据的量纲和标准,减少数据之间的误差。
在对所采集的高校教育成本基本数据进行归一化处理时需要运用最大、最小化进行计算,如公式(1)所示。
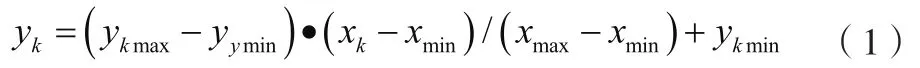
式中:y为归一化后的样本数据值;y和y分别为归一化后的样本数据值的最大值和最小值;x为原始样本数据值;和分别为原始样本数据序列中的最小值和最大值。
1.2 成本核算数据核函数及核参数的确定
将高校教育成本数据进行线性化操作,一方面能够大大增强模型的计算能力,当所要计算的高校成本教育数据信息过于庞大时,该操作能够保证模型正常运行。另一方面,可避免计算时产生较大误差,能够有效提升模型的稳定性和准确性。该文运用核函数对高校教育成本数据进行处理,模型的核函数所在使用位置见表1。

表1 核函数设置表
核函数中的参数是核函数本身自带的,核函数参数的取值规则是定义核函数最重要的标准。该文分别使用了2种不同的核函数进行模型的构建,能够增强模型的稳定性和计算的准确性,避免模型在进行大数据计算时产生误差。
1.3 构建高校教育成本核算模型
构建高校教育成本核算模型时需要运用灵活性较强的算法,这个算法需要效率高、计算精准,以保证模型的稳定性。选择合适的算法来构建模型十分重要,该文采用人工蜂群算法来确定模型参数。人工蜂群算法在每次计算参数的过程中都会进行2次计算,一次是全面计算,一次是局部计算。2种计算方法相结合能够更快更稳定地将模型参数计算出来,并能保证参数的误差在合理的范围内。该文所设计的模型需要在所收集的基本数据中挑选出相对较小的数据作为样本构建模型。为了使构建模型时所用的参数更加合理、全面,需要对所收集来的数据信息进行全方位筛选。
该文所运用的人工蜂群算法中的侦察蜜蜂可通过不断扩大侦查范围、减小数据的极值误差来提高算法的性能。在最开始的原始数据阶段,新产生的资源会替代旧资源,以此来形成循环。这种方法虽然大大减少了数据计算的任务量,但是被替代的旧资源中还存在一部分对模型有用的数据,这就导致模型的基本数据不完善,形成参数时也不能保证参数的准确性,进而使模型在计算高校教育成本时出现误差,削弱了模型的计算性能。
根据以上算法分析可知,使用人工蜂群算法时要对新产生的资源和被替代的资源都进行数据分析,以确保模型数据信息的完整性。所以该文引入Levy飞行算法与人工蜂群算法相结合的方法来计算数据信息。Levy飞行算法能够在直线前进的计算路径中找到一个直角的支线计算路径,能够保证数据信息在筛选、分析的过程中不落下任何信息点,确保模型基本样本数据的全面性和完整性。同样,2种算法相结合能够很好地解决人工蜂群算法的局限性,将被替代的数据资源中的重要信息节点保存下来,并进行整合。一方面能保证数据信息都能够被很好地利用,另一方面也加快了数据筛查、分析的速度,缩短分析的时间,提高了工作效率。2种算法相结合后的计算方法与之前单独使用人工蜂群算法相比,不同的地方就在于侦察蜜蜂的步骤上,改变后的算法如公式(2)所示。

式中:u为任意路径点的选择;、、分别为路径点的坐标号,其中为选定路径点,和为随机路径点,∈{1,2,…,},且≠,NS为资源的最大数量,∈{1,2,…,},为人工设定的边界;()是一个随机数,由Mantegna计算得到,如公式(3)所示。

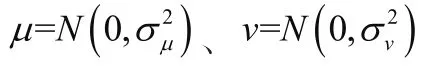

式中:σ和σ分别为函数分布的离散量,Γ() =(-1)!。
这2种算法相结合能够较好地计算出模型构建时所用到的参数。利用参数能够分析出高校教育成本的特点,然后根据不同高校所设置的规范对高校教育成本的影响因素进行具体分析,将这些影响因素整合处理,得到不同因素所占的比例,计算出这些因素的影响因子,输入模型中,以保证模型在核算时能够针对不同的高校进行个性化处理。
该文所设计的高校教育成本核算模型的具体构建流程如图1所示。首先,将所采集的数据进行归一化的预处理,形成模型基本数据。其次,将数据输入模型中,使用试错的方法对第1种练习数据集合进行设置,利用练习数据集合和试验数据集合的设置使建模数据更加完整,强化模型性能。再次,确立核函数及核函数参数,进行模型的构建,增强模型的稳定性和计算的准确性,避免模型在进行大数据计算时产生误差。最后,利用算法计算出合适的模型参数,将参数带入模型中完成构建。最后根据指标评价对模型的性能进行评价。
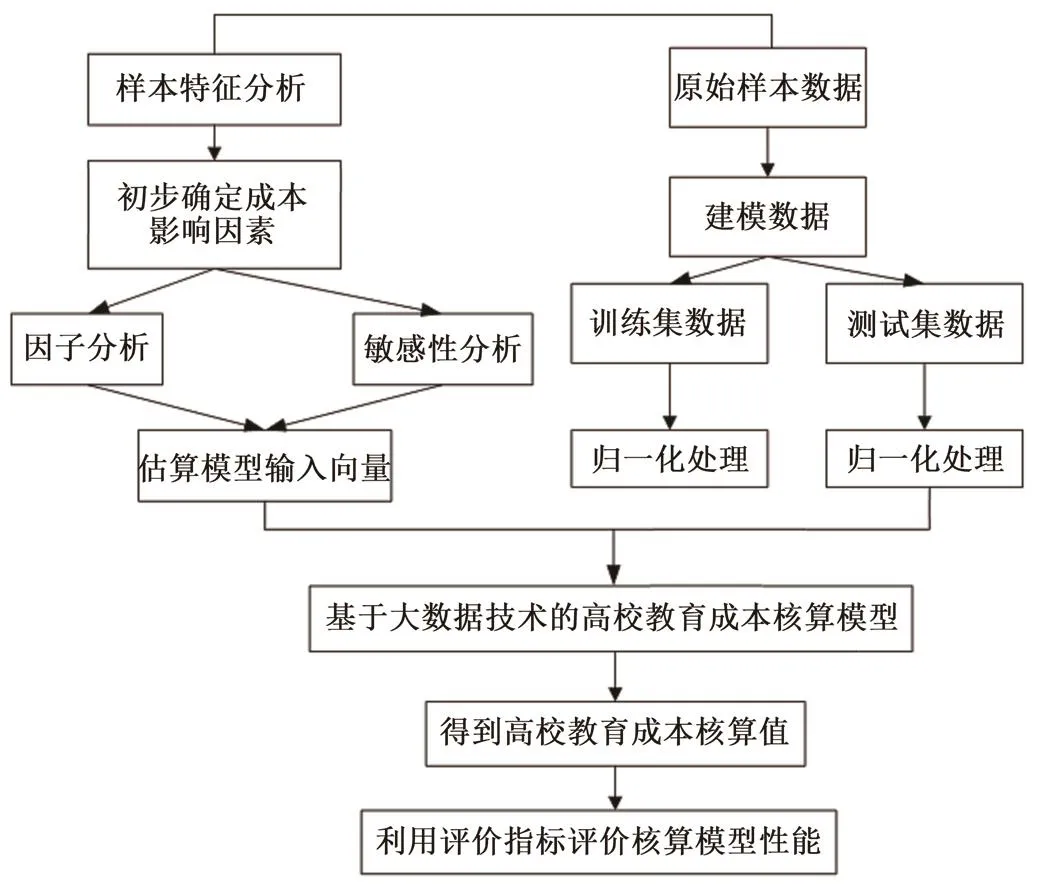
图1 基于大数据技术的高校教育成本核算模型构建流程
2 试验论证分析
为了验证该文所设计的基于大数据技术的高校教育成本核算方法能否准确地将高校教育成本计算出来,该文选取了某高校作为试验对象,收集该高校的教育成本作为建立模型的基础数据。
首先,基于大数据技术对高校教育成本数据进行处理,为了保证高校教育成本的核算精确度,减小误差,需要对高校教育的开支进行全面了解,将每项数据都记录下来。教育成本中最难计算的就是高校固定资产的折旧。通过对该高校的资料收集可以看出该高校的固定资产包括教学楼、宿舍楼和办公楼等各种建筑资产,计算机、电教设备、空调、实验室仪器和体育教学用品等教学用具。根据这些固定资产的使用时间和未来价值进行评估计算,能够得到固定资产的基本数据。再通过对这些固定资产进行评估和折旧处理,将其转换为一定数量的金钱,作为数据输入模型中,能够减少核算误差。
其次,对各初步确定的成本影响因素进行因子分析,以选择的公因子的累计贡献率超过80%为标准提取公因子。该文中不探讨新的公因子的含义,只根据公因子系数的相对大、小判断各初步确定的成本影响因素的重要程度,采用单因素敏感性分析方法,使各成本影响因素变动20%,计算出该影响因素的敏感性系数,判断各影响因素对成本影响程度的相对大、小,同时计算各初步确定的成本影响因素的成本占比,将其作为筛选过程的辅助参考。根据资源的性质可以看出有一部分资源耗费与成本对象有可划分的直接的关系,划分标准就是资源动因,可以通过确定各个作业中心的资源动因数量对各个作业中心应分摊的成本数进行划分。
某些类别的资源花费是专门属于某一个作业的,这些类别的资源花费直接归纳到专属的作业中心中,就能避免选择相应的资源动因对其细分。
在高校的教、职工人员中,岗位划分十分细致,不同岗位的教、职工人员的工资开销也有所不同。所以要根据人数和工资,对不同岗位的教、职工人员进行单独成本核算。不同岗位的教职工人员所占资源的分配见表2。

表2 分配率统计表
最后,提取其中的关键成本影响因子作为模型的输入向量,采用经大数据技术调谐得到的正则化参数C和核函数参数σ的取值,并将不敏感系数ε=0.00作为模型的参数,完成高校教育成本核算模型设计。将测试集数据输入高校教育成本核算模型得到各部分的成本核算值,比较成本实际核算值与该文的该文模型核算值,对比结果见表3。
根据表3可知,测试集中各样本的成本估算值与实际值较为相近,而传统方法核算出的数值与实际数值相差较大,说明利用该问所设计的基于大数据技术的高校教育成本核算模型具有较好的预测精度。该模型改善了传统方法中高校教育成本核算值与实际值相差较大的问题。

表3 成本实际核算值与该文模型核算值的对比结果
3 结语
该文利用大数据技术设计出高校教育成本核算方法。通过大数据技术精确处理高校成本数据,确定成本核算数据核函数及核参数,构建高校教育成本核算模型。根据试验结果可知,运用该文所设计的核算方法能够大大降低核算误差,提高核算的精确度,有助于高校的教育资源管理,为高校管理者提供了科学合理的成本核算方法。但由于时间限制,该文没有对多个高校进行成本核算试验,还需要在今后的研究中进一步完善。
