基于改进人工蜂群算法的多值属性系统故障诊断策略

张志龙，陈 岑，史贤俊，蒋 勇

（1.海军航空大学，山东 烟台 264001；2.中国航天科工集团第二研究院706所，北京 100854）

0 引言

随着航空航天、武器装备等高新技术行业的发展，各种高端设备与产品的功能和结构越来越复杂，对安全运行的要求也日益严苛。测试性可提高系统测试与诊断能力、降低全寿命周期费用，其在装备质量特性中的重要性逐渐凸显。诊断策略作为测试性设计的重要组成部分，对于提高装备故障诊断能力和诊断效率、降低期望测试费用有着重要的意义。

现有的大部分算法研究均是二值系统，即测试结果为“0”和“1”，二值系统的诊断策略问题被证明是NP 完全问题。而实际上，系统的测试结果不只是“通过”和“不通过”，还有可能是多个测试值。有多个测试值的测试被称为多值测试，对应的系统是多值属性系统（Multi-valued attribute system，MVAS）。

目前,许多专家学者对MVAS 的故障诊断策略进行了研究。总体上分为2类：一类是扩展二值测试序列寻优算法，基于测试值以及依赖矩阵的变化扩展传统算法，得到MVAS 的测试序列寻优算法；另一类是将MVAS简化为二值系统，随后运用二值测试序列算法寻找最优测试序列，但简化的MVAS会出现较多的冗余测试与模糊故障，从而遗漏许多测试信息。针对现有的研究，发现这些优化方法存在以下缺陷：

1）现有优化算法的优化目标单一，忽略了漏检、虚警等不确定信息，使得最终的诊断策略最优性难以保证；

2）传统的群智能算法与诊断策略寻优过程存在差异，容易简化一些关键性问题，因此，寻优过程与群智能算法实现过程的合理融合是该类算法应用于MVAS诊断策略优化的关键。

人工蜂群算法（Artificial Bee Colony Algorithm，简称ABC 算法）作为群智能算法的主要代表，已成功解决了许多NP 完全问题，但却无法直接应用于故障诊断策略。本文提出用ABC 算法向测试序列寻优过程拟合，改进后的ABC算法，记为NABC算法，通过制定状态转移规则和方向信息矩阵更新策略，实现NABC 算法与MVAS 诊断策略融合，并用导弹舵系统实例验证了NABC算法的正确性。

1 诊断策略优化问题数学描述

1.1 构成要素

1.2 诊断策略优化目标

本文从测试成本、故障隔离时间、测试错误代价入手，建立多值测试故障诊断模型，开展诊断策略设计。诊断策略的3个优化指标计算公式如下。

1）平均测试成本。诊断策略优化问题最关注的就是测试成本。一般情况下，故障状态的检测和隔离是一系列测试设备工作和人为参与的结果，故该指标是开展故障诊断策略优化最主要的评价指标。诊断策略对应的测试费用越低，诊断策略就越优，平均测试成本，如式（1）所示。

2）平均故障隔离时间。系统一旦发生故障，维修测试人员通常希望能够以最短的时间隔离故障，确定故障源以便于下一步维修。本文用隔离故障过程中所需的平均测试步骤来表示所需的测试时间，故障隔离所需测试时间越少，诊断策略就越优，平均故障隔离时间，如式（2）所示。

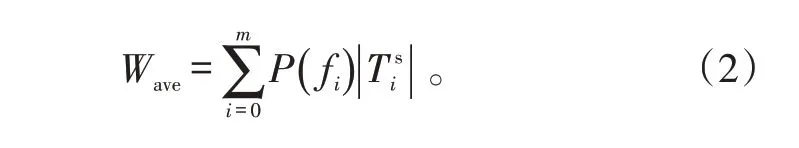
3）平均测试错误代价。由于测试不可靠因素的存在，测试会发生错误，使得本应被检测出的故障被漏检，正常的元件反而被“误诊”，由此产生“误诊”和漏检代价叠加的情况。平均测试错误代价，如式（3）所示。

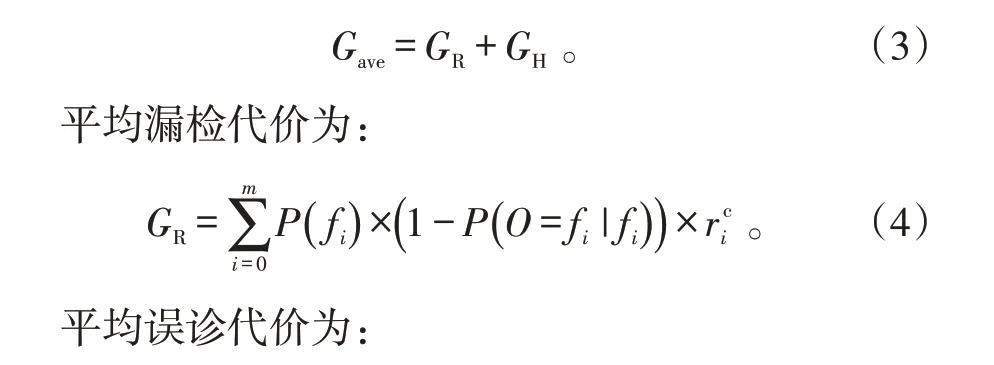
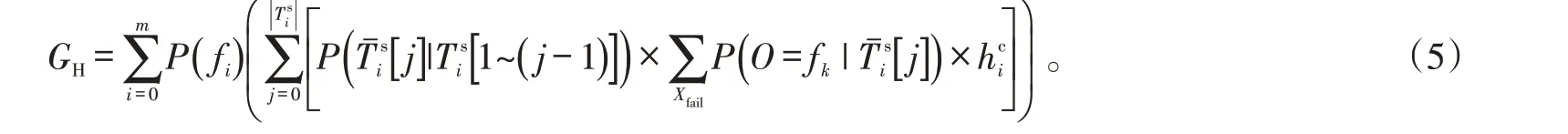
2 基于NABC算法的诊断策略优化方法

ABC算法无法直接应用于故障诊断策略，原因在于大部分算法都是将测试序列寻优过程向蜂群算法转化，导致其搜索过程仅能确定1个测试，而不能为每个子集寻找最优测试，致使诊断结果差、运行时间长。

下面介绍ABC 算法向测试序列寻优过程拟合过程。

2.1 蜂群搜索过程

为将ABC算法与MVAS测试序列寻优过程融合，本文重新定义蜂群算法搜索过程。设定1 个蜂群（故障集）由个不同批次蜜蜂组成，蜂群被随机放置某一位置（测试点）上，然后放任不同批次的蜜蜂寻找各自的最优食物源，寻优过程中每个食物源的位置代表1 个测试候选解，而所拥有的蜜量代表相应方向上的选择概率的大小。

蜂群中的个体根据某种规则选择寻找最优食物源的方向（测试），按照方向上设置的分流点（测试值）蜂群被分割为多个子蜂群，子蜂群重复上述选择方向、分割种群的操作，直至所有批次的蜜蜂均已找到最优食物源。

设定子蜂群规模小于等于1，即找到最优食物源位置，此时认为最后选择的测试即为最优食物源的位置所在，而蜜蜂寻找食物源时依次选择的测试构成了诊断隔离故障的测试序列。

上述蜜蜂寻优的过程如图1 所示，图中的、…、a表示测试值，即分流点。

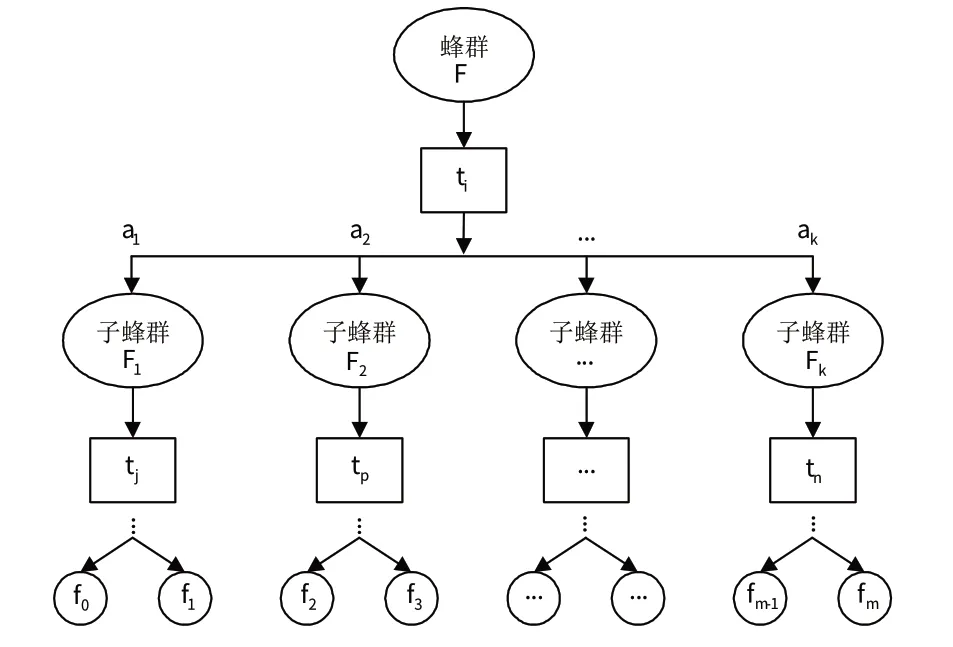
图1 蜜蜂寻找最优食物源的搜索过程Fig.1 Process of bees searching for the optimal food source

为直观介绍重新定义的人工蜂群，对比五元组在MVAS诊断策略和NABC算法中的含义，如表1所示。

表1 MVAS诊断策略和NABC算法的五元组对比Tab.1 Comparison of five-tuple for MVAS diagnostic strategy and NABC algorithm

由表1 可知，重新定义的蜂群使得MVAS 的五元组有了新的含义，在此基础上，还应设置状态转移规则、确定方向信息初始化及更新方式，才能实现所提算法在MVAS中的应用。

2.2 状态转移规则

传统的ABC 算法通常以观察蜂得到的食物源选择概率来选择最优食物源，而本文所提算法中定义的蜜蜂批次不同，为避免不同批次蜜蜂寻优过程混乱，故为不同批次蜜蜂设置不同的方向选择概率，以表示测试间的关系，引入概率信息矩阵，如表2所示。

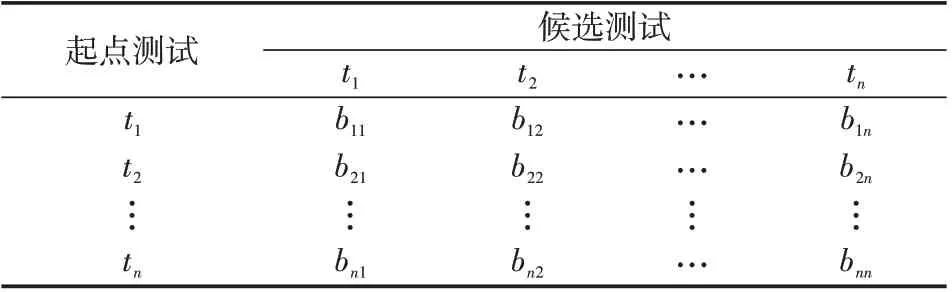
表2 方向概率信息矩阵Tab.2 Direction probability information matrix

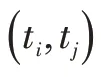
2.3 方向选择概率更新

2.4 算法的实现流程

基于上述分析，NABC算法流程图，如图2所示。

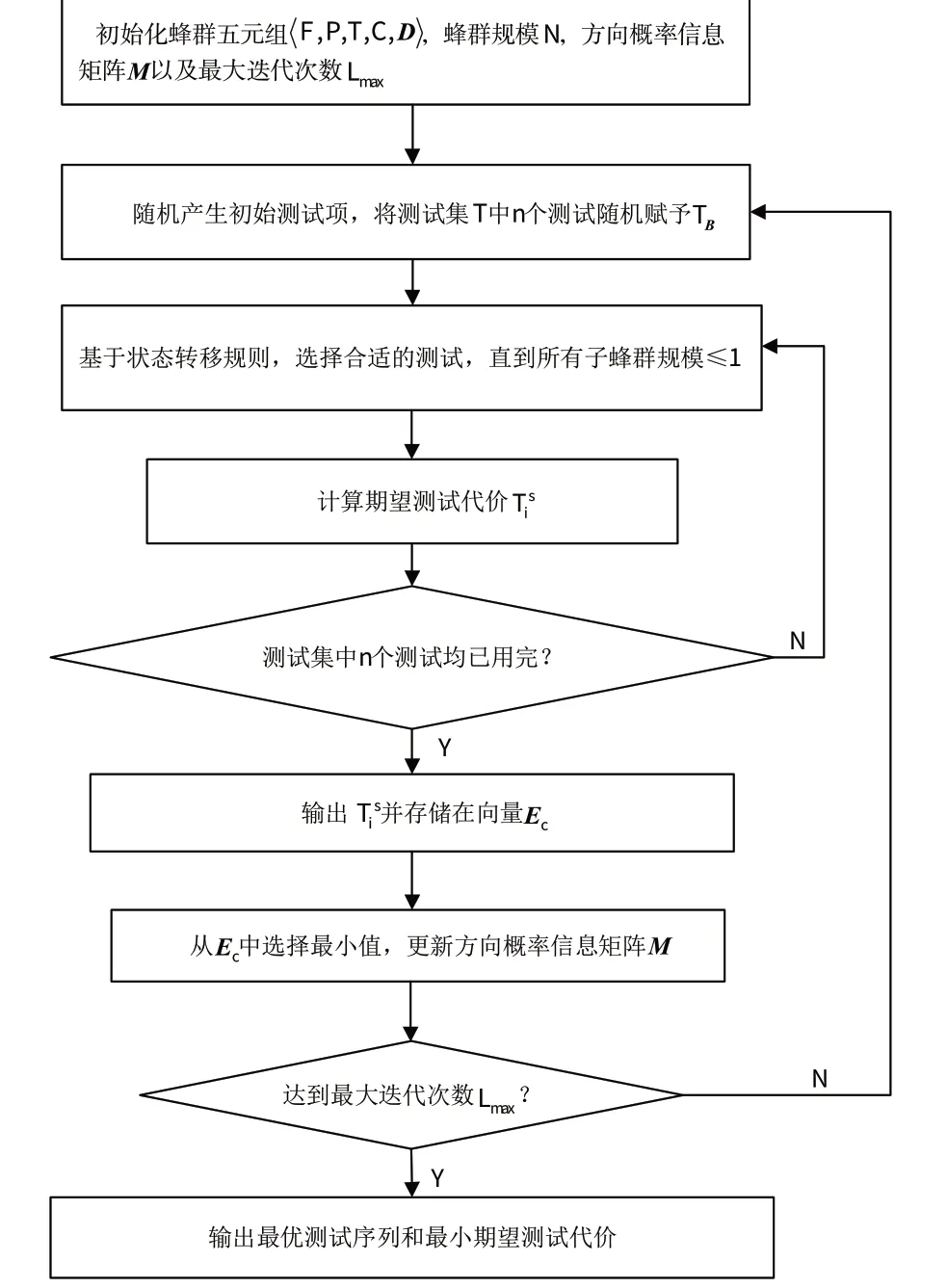
图2 NABC算法流程图Fig.2 Flow chart of NABC

NABC算法具体流程步骤，如下所示。

STEP 2：生成1 组1 维的向量，将测试集的个测试随机赋予。

STEP 3：随机将蜂群放置到的测试上，运用该测试将蜂群分割为个子蜂群。

STEP 4：利用式（7）和（8）从测试集中为个子蜂群选择测试，并在每次选择时留下一定量的观察蜂，记录该测试的方向选取概率，直到所有的子蜂群规模均小于等于1，存储每个蜜蜂的测试序列。

3 实例应用与算法分析

3.1 导弹舵系统实例应用

以某型导弹舵系统及其放大器模块为例，分别开展多值测试诊断策略优化设计工作，由于本文研究的系统为多值属性系统，测试对不同的故障程度有不同的响应，故给出舵系统及其放大器模块对应的多值相关性矩阵，见图3和图4。

图3 舵系统的多值相关性矩阵Fig.3 Multi-valued correlation matrix of the rudder system

图4 舵放大器电路的多值相关性矩阵Fig.4 Multi-valued correlation matrix of the rudder amplifier circuit

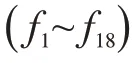
表3 故障模式及相关信息Tab.3 Failure mode and correlation information

表4 测试及测试信息Tab.4 Test and test information

舵系统及其放大器两层次的测试成本、故障“误诊”和漏检代价，见表5。其中，测试成本与测试错误代价并无量纲，是1个以某测试成本或某故障“误诊”、漏检费用为基准的相对值。

表5 两层次测试成本及错误诊断代价Tab.5 Two-level test cost and error diagnosis cost

首先，建立两层次数学模型，均采用式（6）；其次,运用本文所提的算法，参数设置分别为蜂群规模为60，迭代次数为20，初始方向选择概率均为1，3种代价权重系数均设置为1/3；最后，分别针对舵系统层次和放大器电路层次开展诊断策略优化设计工作。

表6给出3种算法得出的舵系统层次诊断策略方案对应的评价指标，由于本文算法的平均测试成本和平均故障隔离时间明显减少，故选择NABC算法进行诊断策略优化。

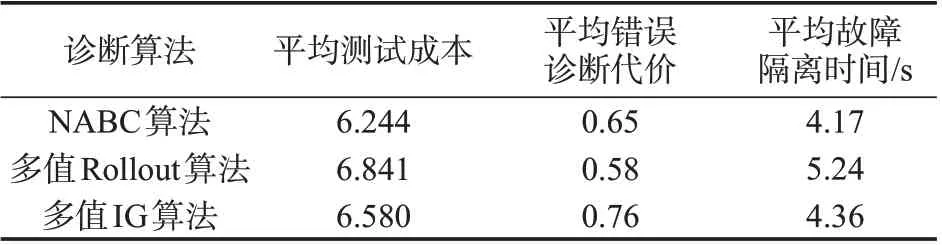
表6 不同算法诊断策略指标对比Tab.6 Comparison of diagnosis strategy indicators of different algorithms

现给出本文算法对应的诊断树，如图5 所示。可以看出，舵系统诊断策略中存在故障模糊组、和，即电动机模块故障模式难以通过现有可用测试进行隔离，需要额外添加测试项进一步进行隔离诊断分析。

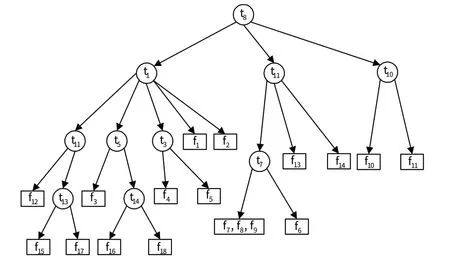
图5 舵系统诊断树Fig.5 Diagnostic tree of the rudder system

同理，将蜂群起点测试依次选为～，得到对应的测试代价，比较得出的测试代价最小，故放在上的蜂群获得最优方向。然后，根据式（9）和（10）更新该方向上的观察蜂数目，即方向概率信息矩阵，继续循环直至达到最大迭代次数。在此给出舵系统放大器模块的诊断树，如图6所示。

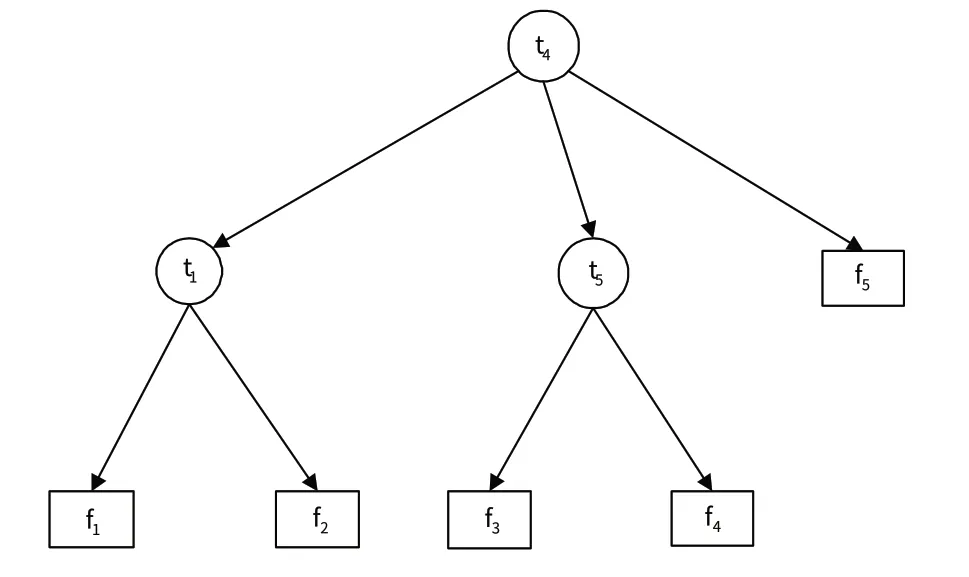
图6 舵系统放大器模块诊断树Fig.6 Diagnostic tree of rudder system amplifier module

经过诊断策略对比可知，NABC 算法相比于其他算法，较好地兼顾了测试成本和故障隔离时间。通过图5 和图6 的故障诊断树可以看出，利用NABC 算法进行诊断策略构建，不仅满足了实际工程中多值系统的测试诊断需求，而且在测试诊断过程中很好地兼顾了测试成本、故障隔离时间和错误诊断代价。

3.2 算法分析

下面进行诊断策略优化算法分析，用MATLAB编程仿真，并将NABC算法与传统故障诊断算法——多值Rollout 算法、多值IG 算法和ABC 算法，进行比较分析。

用以上4种算法在20、40、60维方阵中分别运行，且方阵元素在{0，1，2，3}中随机取值，测试费用在1～2之间随机取值，算法的种群数量设置为方阵阶数，最大迭代次数为20，算法运行次数设为10次。本文主要分析期望测试费用与运行时间2 项指标，图7 是维数为60的10次计算结果。

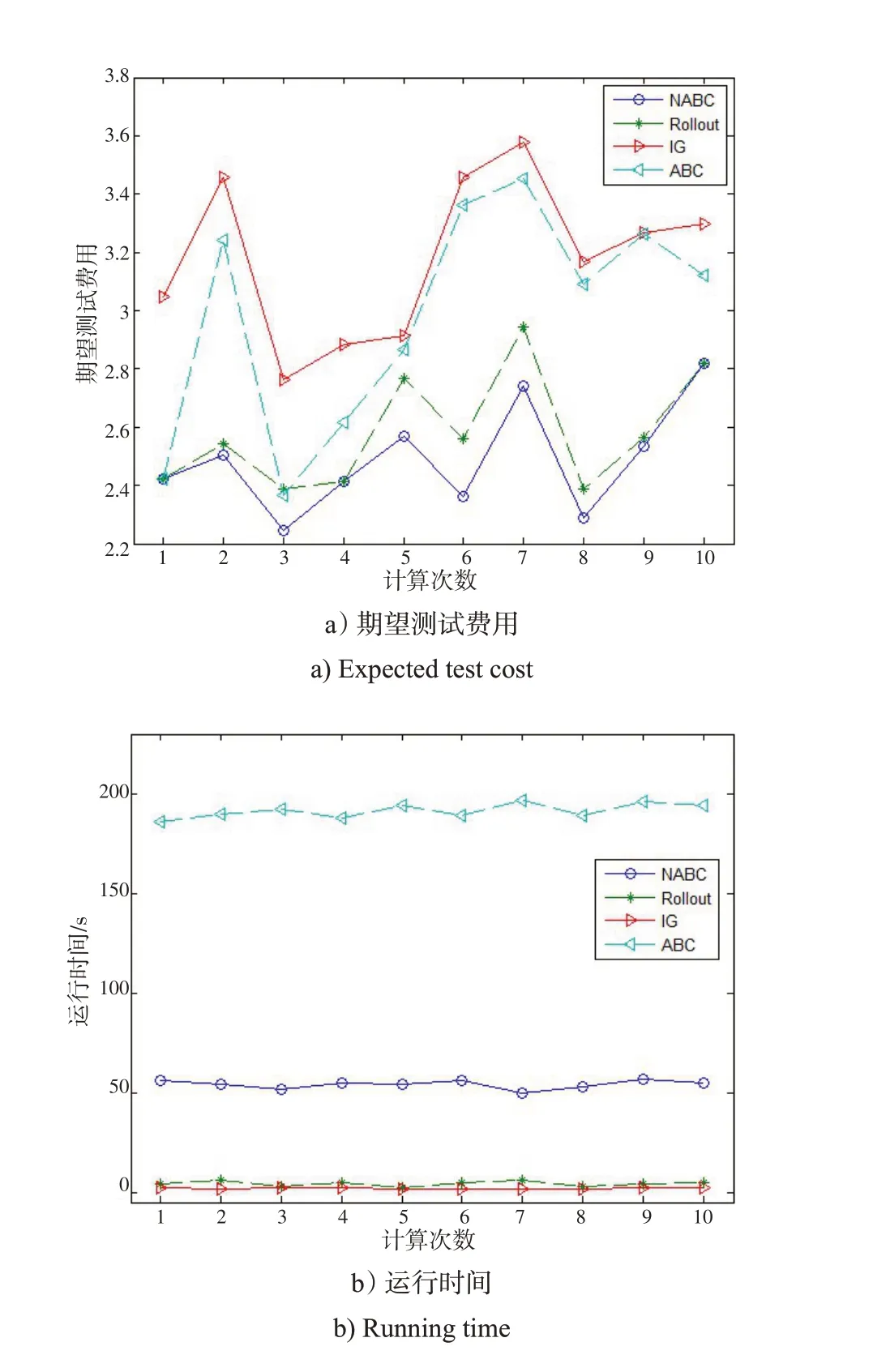
图7 基于4种算法的多值D60×60 矩阵计算结果Fig.7 Calculation results of multi-valued matrix D60×60 based on four algorithms

由图7 可知，NABC 算法的平均期望测试费用和平均运行时间均小于ABC算法，原因在于本文将蜂群算法实现过程简化并重新定义，以实现与MVAS诊断策略寻优过程的融合，同时引入方向概率信息矩阵，为算法的状态转移增加指向性，改善了诊断策略的结果和算法的寻优速度。而ABC算法则对参数要求高，循环次数较多，造成诊断结果差、运行时间长的问题。

NABC 算法的平均期望测试费用小于多值Rollout算法，而平均运行时间大于多值Rollout算法，这是因为NABC 算法的迭代优化了蜂群寻找最优食物源的过程，获得了更好的测试序列，同时也因为迭代次数的增多使得运行时间增加。

与多值IG算法相比，NABC算法的平均期望测试费用较小，这是因为多值IG 算法是1 种贪婪算法，只能实现一步向前寻优，而NABC算法可实现多步向前寻优，从而可获得近似最优结果，而平均运行时间的增加也是由于迭代次数的增多造成的。

4 结束语

诊断策略优化问题是典型的组合优化问题，目前提出的启发式搜索方法大多仅考虑测试成本，难以满足装备测试实际需求，不能实现快速有效寻优。同时，多值测试的诊断策略优化设计问题是1 个计算爆炸问题，全局最优算法不适用于复杂多值属性系统测试诊断策略优化。本文在传统ABC算法的基础上，研究了工程上应用更多的多值属性系统故障诊断策略问题，提出将蜂群算法实现过程简化并重新定义，以实现与MVAS诊断策略寻优过程的融合，同时以观察蜂概率选择食物源为启发，引入方向概率信息矩阵，为算法的状态转移增加指向性。经导弹舵系统实例验证，证明了本文提出的算法能获得较优的诊断策略，是1种有效的方法，具有一定的应用价值。