面向构造分析的赤平投影的计算机实现与应用
2022-08-04毛先成
毛先成
(1. 有色金属成矿预测与地质环境监测教育部重点实验室, 湖南 长沙 410006;2. 中南大学地球科学与信息物理学院, 湖南 长沙 410006)
0 引 言
传统地质构造方面的研究有助于理解矿产资源的形成机制,某些矿体的产状和形态与断层之间存在直接的决定关系,断层对产状资源的分布有着重要的影响(李忠权等,2010),矿液的汇集、渗透、分布和上涌需要节理提供空间条件(陈进等,2018)。因此,研究矿床的地质体数据能够为矿产资源的勘探提供指导。
赤平投影是常用的地质构造分析方法,通过统计节理的倾向和倾角数据,可得到研究区节理的优势方位(陈丽芹等,2014)。目前,虽然赤平投影等地质构造方法的分析软件种类繁多,但大多不是开源软件,在处理数据时存在数据泄露的风险,而且目前暂无系统介绍赤平投影在节理优势方位处理方面的资料。
因此,通过推导绘制赤平投影弧和节理优势方位计算模型算法,使用C++语言进行编码,实现赤平投影的可视化程序,并以胶西北多处金矿床为研究对象,验证开发程序的正确性和实用性。
1 赤平投影原理与绘制
1.1 赤平投影
1.1.1 投影原理 赤平投影以投影球南北方向的顶点为极点,以极点为发射点,将投影球与空间中任意线状或面状实体相交的点或曲线投影到赤平面上。赤平投影具有简单明了、直观形象和综合性强的特点,广泛应用于地球科学中(廖国华,1979)。

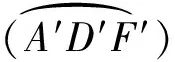
1.2 绘制赤平投影弧
1.2.1 计算圆交点坐标 赤平投影弧是产状数据所对应的圆在基圆内部的弧段,因此绘制赤平投影弧需要先计算产状数据所对应的圆与基圆的交点。计算机中的圆用半径R和圆心坐标(x,y)存储,根据2个圆的半径和圆心坐标即可求出2个圆的交点。已知圆A和圆B相交于点C、D(图3),圆A的圆心坐标为A(x1,y1),半径为r1;圆B的圆心坐标为B(x2,y2),半径为r2。交点C和D的坐标推导公式如下。
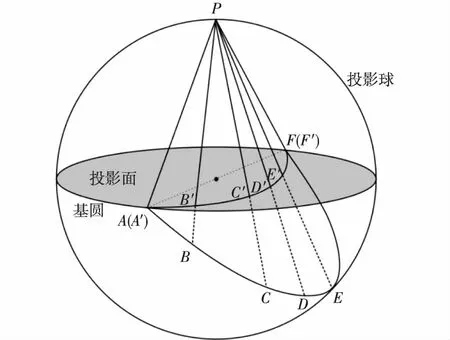
图1 平面赤平投影原理Fig. 1 Stereographic projection principle
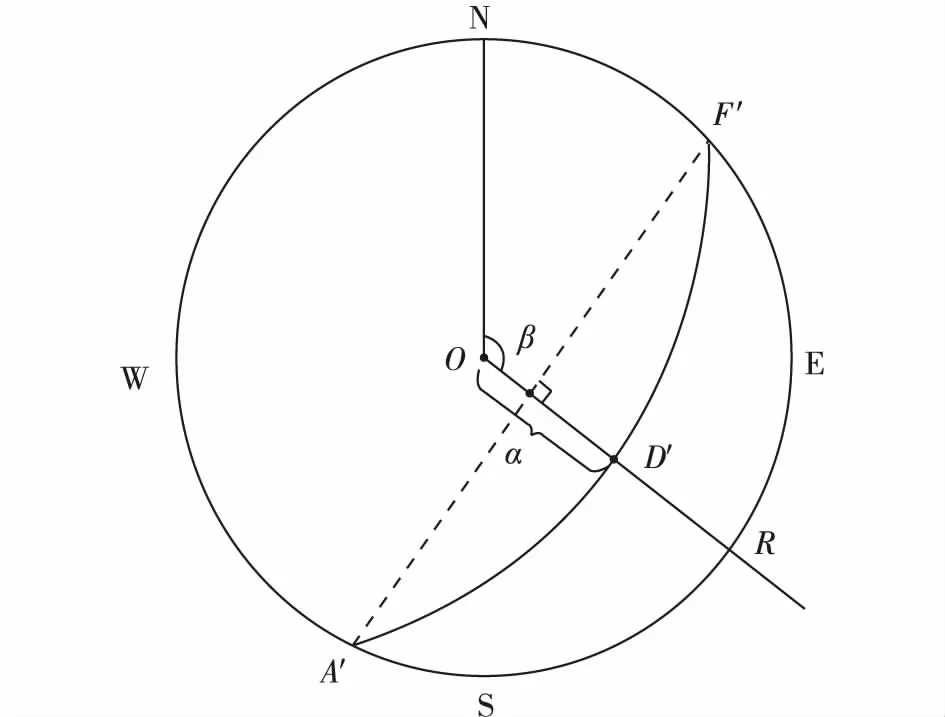
图2 赤平投影图构成Fig. 2 Structure of stereographic projection
绘制辅助线(图4),其中直线AB=L,直线AB的斜率为K1,直线CD的斜率为K2,则有:
(1)
解得:
(2)
(3)
(4)
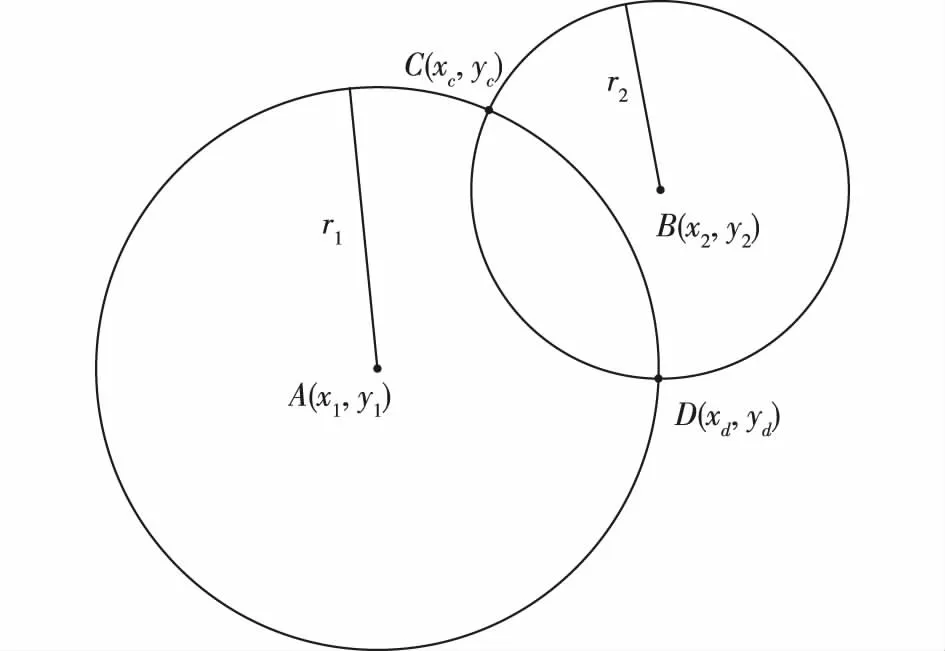
图3 平面两圆相交Fig. 3 Intersection of two circles on a plane
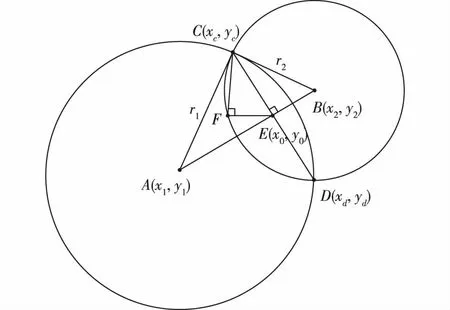
图4 求两圆交点示意图Fig. 4 Calculating the points where two circles intersect
1.2.2 计算机绘制吴氏网 赤平投影常用吴氏网作为投影网。吴氏网由1个基圆和1组经纬线构成(图5),基圆圆周以北方向N为0°,顺时针方向0°~360°,节理倾向方位与圆周方位对应,圆周到圆心为0°~ 90°,节理的倾角方位与半径方位对应。
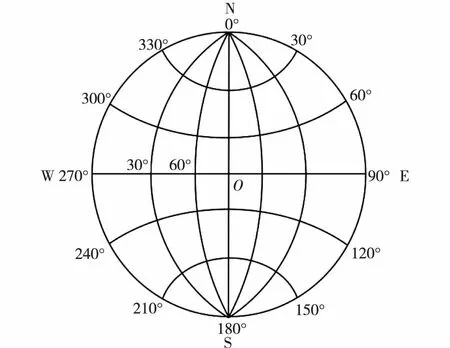
图5 吴氏投影网Fig. 5 Wulff net
首先绘制基圆,其半径为20 cm,在计算机制图时,为方便尺度换算,半径设为200 px。
绘制经线,吴氏网中每条经线均为圆心坐标在X轴的半径不同的圆在基圆内部的弧段。以这些圆的圆心至C点(或D点)的距离为半径,绘制一系列通过C、D点的圆弧,得到吴氏网一侧的经线,同理绘制另一侧经线(冯明权,2009)。设基圆的半径为R,产状数据投影到基圆的圆弧的圆心为F(图6),其坐标为(x,y),则:
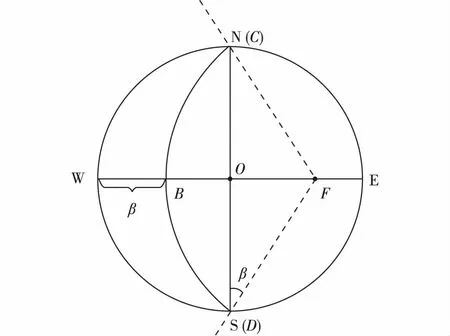
图6 投影网经线绘制Fig. 6 Meridian drawing of the projection net
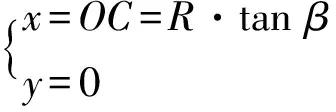
(5)
圆弧的半径为r,长度为:
(6)
式(5)、(6)中,β为产状平面的倾角,(°)。
将基圆与圆F的半径和圆心坐标代入公式(3)和(4),求得交点C、D的坐标,在基圆内部的圆弧部分即为组成吴氏网的南北经向部分。赤平投影弧的绘制仅用到吴氏网经线的绘制方法,不再介绍计算机绘制吴氏网纬线的方法。
1.2.3 绘制任意产状的赤平投影弧 在手工绘制某节理的赤平投影弧时,需要固定吴氏网,根据节理的走向旋转相应的角度,再根据倾角选取相应南北走向的经线作为该节理的赤平投影弧。
在计算机中,为避免手工绘制之类的操作,可采用以下方法,即在绘制吴氏网的南北向经线时,每条经线都代表倾向相同的节理,其圆心均在X轴上,只是每个节理的倾角不同,所以圆心的位置不同。
如图7所示,以某节理赤平投影弧所在圆的圆心O2至基圆圆心O1的距离L12为半径,以O1为圆心绘制圆C1,在圆C1上倾角处处相同,根据倾向可推导出该赤平投影弧所在圆的圆心O2的坐标,推导公式如下。
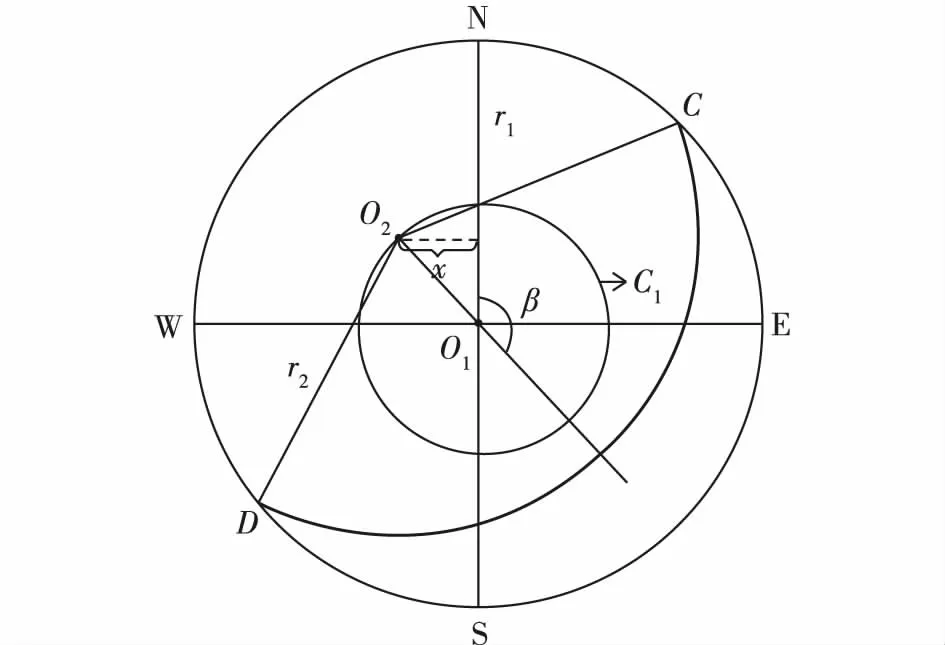
图7 任意产状赤平投影弧Fig. 7 Stereographic projection arc of arbitrary occurrence
由公式(6)得到圆C1的半径,即L12的长度,圆C1的标准方程为:
(7)
赤平投影弧所在圆的圆心在圆C1上,其圆心坐标的推导公式为:
(8)
式(8)中,β为节理的倾向,(°)。

1.3 优势方位计算模型
1.3.1 绘制等密图 计算节理组产状数据的优势方位通常采用等密图的方式。等密图是属性特征为密度的等值线图,后者的绘制通常在规则格网或三角网中对离散点进行插值处理,然后通过追寻等值线,最终绘制成图(龚恒等,2015)。等值线图的绘制方法已经很成熟。
首先通过公式(9)将产状数据投影到施密特网。施密特网与吴氏网的结构相似(陈胜同等,1996),不同之处在于施密特网从圆心到圆周对应的是0°~90°,每条产状数据在图上均为一个离散点。为保证施密特网圆周附近的离散点能够按照叠加对折原理处理,需将圆周边缘的离散点对折到圆的另一端(余淳梅等,2008)。
(9)
将施密特网的外接矩形划分为若干等分的规则格网,统计落入每个2×2单元大小格网内切圆中的离散点个数,将离散点个数除以总散点数的结果作为该格网中心点位置的密度值;顺序追踪图中密度值相同的格网中心点,连接所有等密度线,得到等密图。
1.3.2 计算优势方位 追踪得到的每条等密度线均包括一些格网中心点,通过对等密度线内的格网中心点进行处理,得到局部区域的优势中心。从若干条封闭型等值线中选取达到等值线最高值一半的等值线(李国庆等,2008),统计落入这些等值线的格网点,计算坐标的加权平均值,作为局部区域的优势中心。
设某条等值线所围的格网点坐标为(xi,yi),Hi为该格网点的密度值,则
(10)
求得的(x,y)即为施密特网下优势方位的直角坐标,代入式(11)得到节理的优势方位(β,θ)。
(11)
2 赤平投影程序设计与实现
2.1 程序设计
2.1.1 交互设计 所设计程序在Microsoft Visual Studio 2012(vs2012)平台进行开发,在Windows桌面平台运行。程序界面交互设计选择微软基础类库(MFC)框架,它不仅是一个以C++类的形式封装的Windows API类库,还是一个桌面程序开发框架。在vs2012开发平台中创建一个MFC项目不需要考虑消息传递等底层逻辑,仅需考虑程序的实现逻辑,程序逻辑的实现使用C++语言,能够直接继承MFC函数库中的类和方法。数据存储使用CSV文本文件,它具有轻量级、易安装的特点,非常适用于小型程序。程序的交互界面设计见图8。
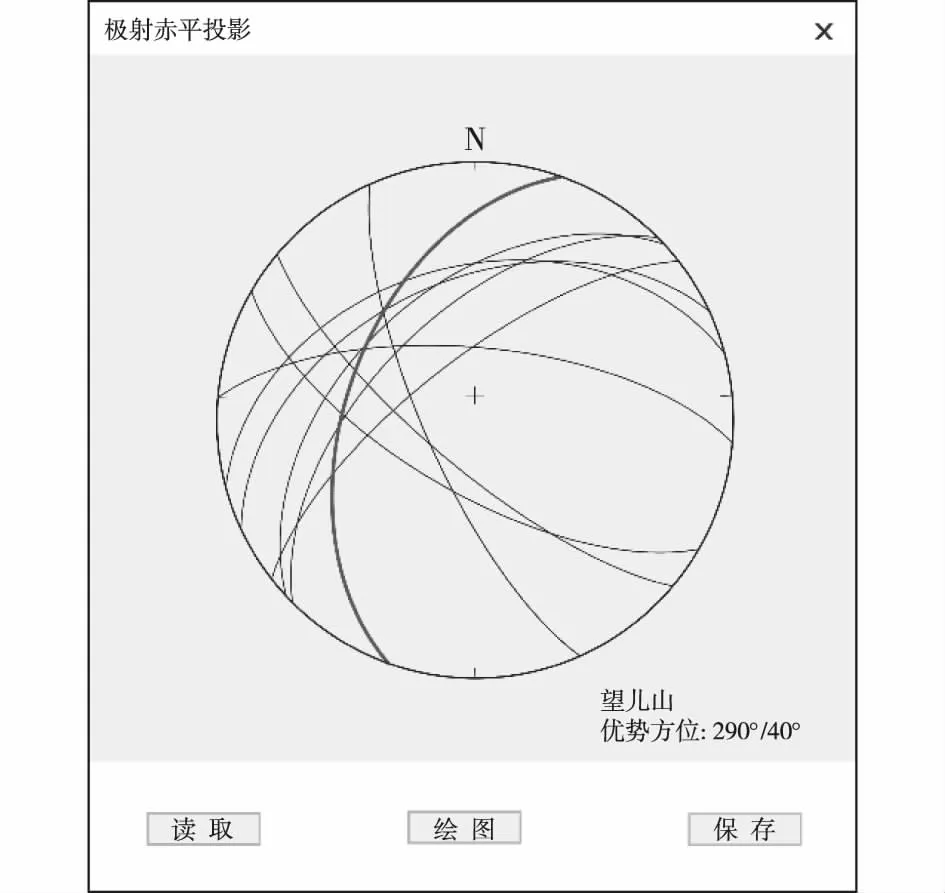
图8 程序交互界面Fig. 8 Program interface
2.1.2 运行流程 (1) 读取某研究区的节理数据,然后根据各节理的倾向和倾角数据绘制对应的赤平投影弧。
(2) 对数据进行处理,将产状数据转化为施式网直角坐标系下的数据,并通过规则格网进行统计。
(3) 根据设置的等值线等级,在规则格网中进行等值线追踪,选择等值线中最高级别一半等级所包含的区域,计算优势方位。
(4) 绘制优势方位所对应的赤平投影弧,并将可视化结果输出。
程序运行流程见图9。
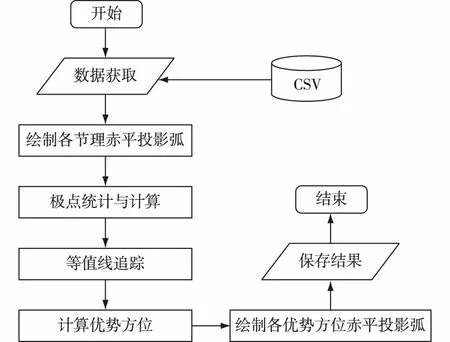
图9 程序运行流程图Fig. 9 Program flow chart
2.2 关键过程实现
赤平投影的绘制过程主要由赤平投影弧绘制和优势方位计算组成。
2.2.1 赤平投影弧 仅存储1条赤平投影弧,包含该弧段的起点和终点位置、宽度和颜色等属性、计算交点及绘制方法等。具体结构如下。
Class sgp_pjt_arc{
int m_r; //弧段所在圆的半径
intm_width; //弧段的宽度
Color m_rgb; //弧段的颜色
double m_dip, m_dip_dir; //倾角和倾向
Point m_start_p, m_end_p; //起点终点位置
…
void draw_arc(); //绘制弧段
sgp_pjt_arc( double dip, double dip_dir );
//类的构造函数
Pair
double r1, double r2, Point p1, Point p2 ); //求两个圆的交点
int cal_arc_radius(double R, double dip_dir ); //计算圆弧所在圆的半径
…
}
2.2.2 优势方位计算模型 包括节理数据的转换、极点统计与计算、等值线追踪和优势方位计算等过程。具体结构如下。
Classpri_orientiation{
Line m_max_countor; //级别最高等值线
Pair
Array
Array
Array < Pair
Array
…
Array
Array < pair
voidstatistics_density( Array
Array
Array
Pair
…
}
3 赤平投影应用实例
3.1 研究区地质背景
胶西北金矿矿集区矿产资源丰富,已探明金矿资源储量占胶东地区总储量的90%以上,中型以上金矿床达28处,胶东地区的特大型金矿均产于该地区(宋明春等,2011)。胶东金矿床具有区域集中、规模大、富集强度高和成矿期短的特点,区内包括三山岛断裂带、焦家断裂带、招平断裂带3条主要含矿断裂带(图10)。
三山岛断裂带位于胶西北最西部三山岛—仓上一线,陆地延伸约10 km,断裂的两侧延入渤海。该断裂带严格控制着一系列金矿床的产出,如三山岛、仓上等金矿(肖风利等,2018)。断裂的总体走向为NE-NNE,局部为NE-NEE。
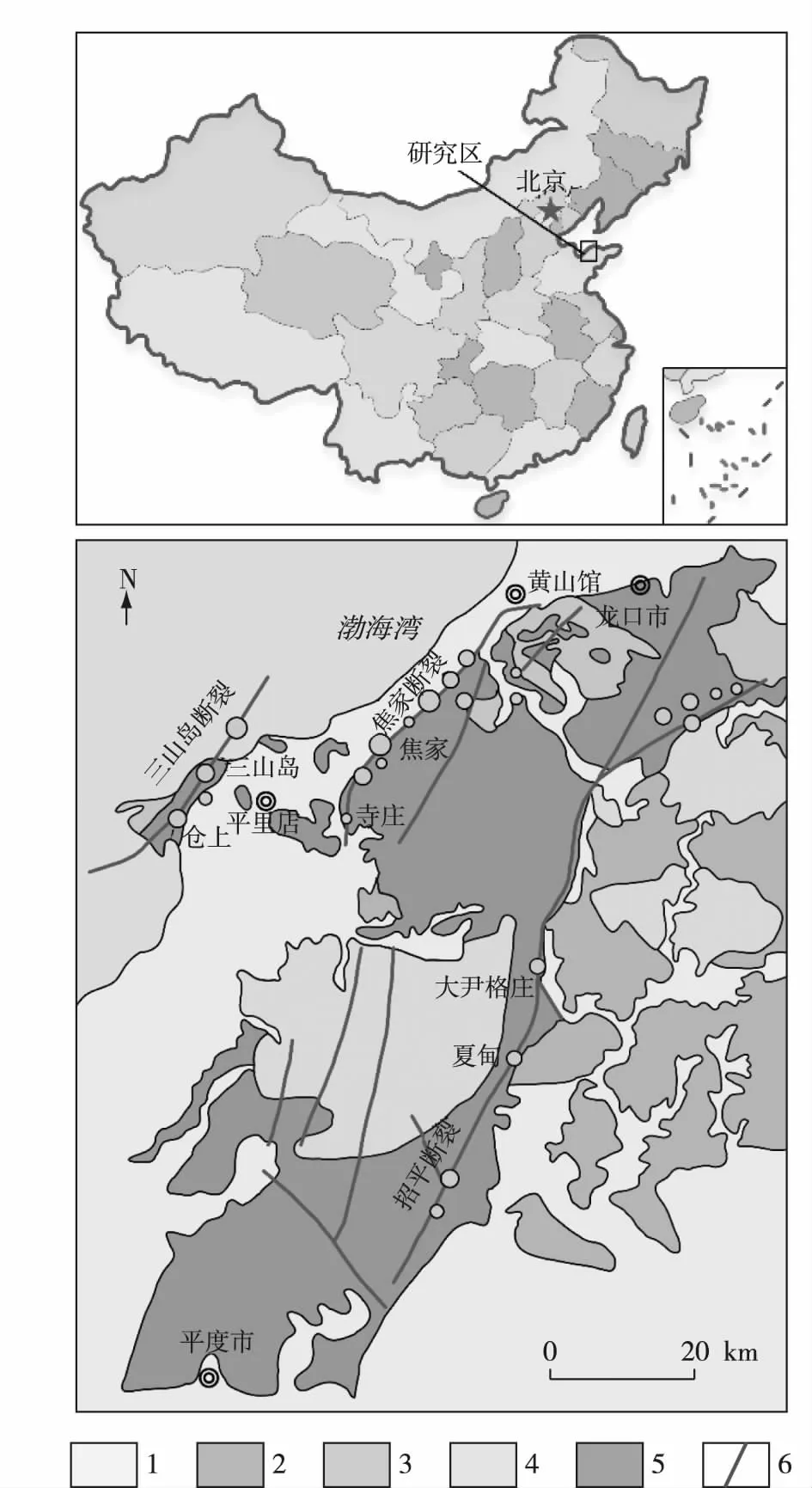
图10 胶西北地质简图(据Yang et al., 2016; Mao et al., 2019修改)1-第四系;2-上太古界胶东群;3-早白垩世郭家岭花岗闪长岩;4-晚侏罗世栾家河二长花岗岩;5-晚侏罗世玲珑花岗岩;6-区域断裂Fig. 10 Simplified map of northwestern Jiaodong Peninsula(modified from Yang et al., 2016; Mao et al., 2019)
焦家断裂带位于平里店—黄山馆一带,总长度为27 km,宽80~500 m,区内发育新城、红布、寺庄等金矿床(苏旭亮等,2016;王金利等,2020)。
招平断裂带北起龙口颜家庄,南至平度、洪山一带,断裂全长200 km,宽150~200 m,区内发育大尹格庄、后仓、夏甸等金矿床,断裂总体走向为NE-NNE,从北到南整体呈S形展布。
3.2 节理优势方位处理与分析
研究范围包括三山岛、寺庄和夏甸3个矿区,处理对象为3个矿区成矿期的节理数据。
(1) 绘制矿区节理数据的赤平投影弧(图11)。图中从左到右依次为三山岛、寺庄和夏甸不含优势方位的赤平投影图。
(2) 统计各矿区的节理数据,绘制各矿区的极点等密图(图12)。通过优势方位计算模型,得到各矿区优势方位的数据(表1)。

表1 各矿区节理优势方位
(3) 根据得到的优势方位,绘制各矿区节理数据的赤平投影图(图13)。
图13显示:三山岛矿床位于三山岛断裂带,走向为NE-NNE(图13a),处理得到的结果符合实际区域地质构造;寺庄矿床位于焦家主断裂带的南部,走向为NNE-NE(图13b),与焦家主断裂的走向相同;夏甸矿床位于招平断裂带,结果显示矿床断裂走向为NE-NNE(图13c),与招平断裂带的走向一致。
Dips是一个轻量级、易操作的地质绘图软件,常用于绘制玫瑰图、极点图和等密图等。使用Dips软件处理3个矿区的产状数据,利用其等密图功能计算3个矿区的优势方位,并与自编软件处理得到的优势方位进行比较(表2)。
由表2可知,自编软件计算的优势方位与Dips软件处理得到的结果误差在±2°以内,结果的精度符合实际需求,且各矿床的优势方位符合预期,与该矿床多数产状数据的方位相似,所编写程序绘制的赤平投影图能够满足实际需求。
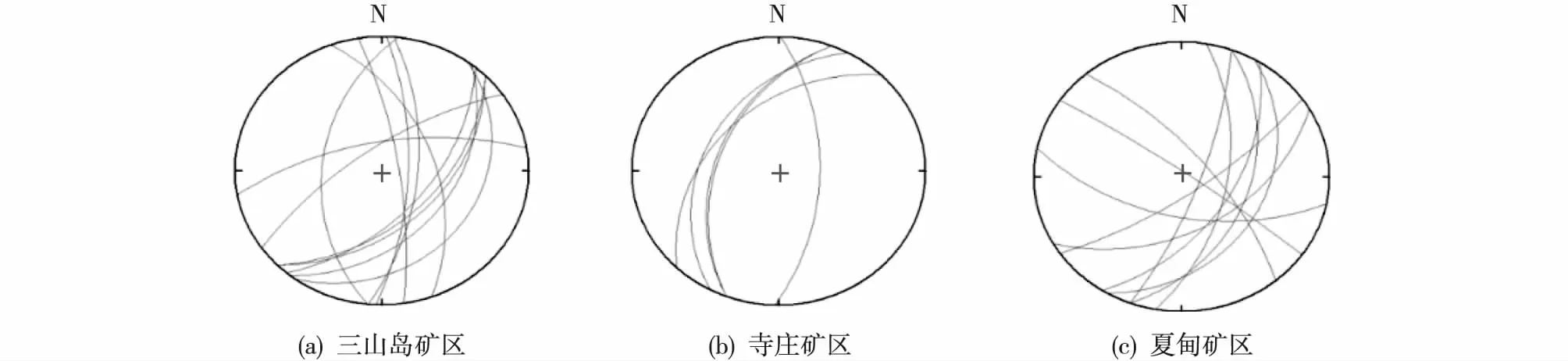
图11 不含优势方位的赤平投影图Fig. 11 Stereographic projection without dominant orientation (a) Sanshandao mining area; (b) Sizhuang mining area; (c) Xiadian mining area
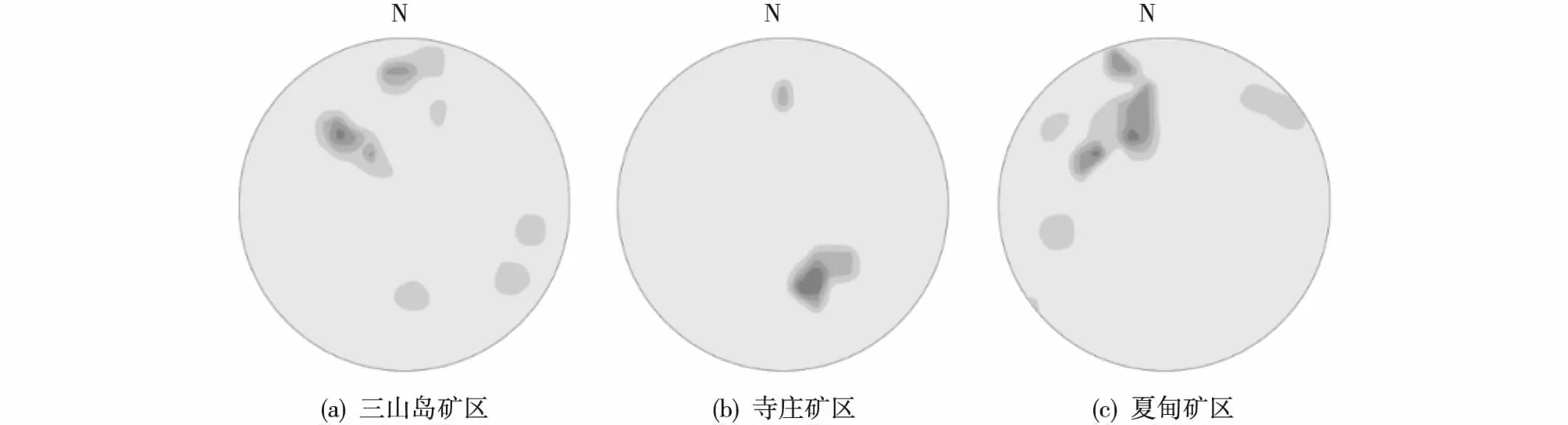
图12 各矿区节理等密图Fig. 12 Isodense map of joints in each mining area(a) Sanshandao mining area; (b) Sizhuang mining area; (c) Xiadian mining area
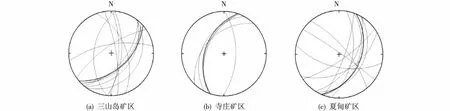
图13 各矿区节理数据赤平投影图Fig. 13 Stereographic projection of joints in each mining area(a) Sanshandao mining area; (b) Sizhuang mining area; (c) Xiadian mining area
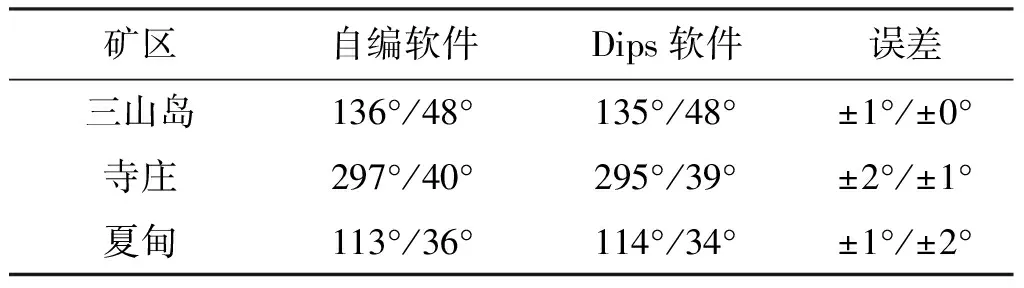
表2 各矿区节理优势方位Dips软件处理结果
4 结 论
(1) 详细推导了赤平投影弧的绘制和优势方位计算模型的算法,阐述了程序设计和实现的过程,提供了系统的赤平投影在节理优势方位处理方面的资料。
(2) 以胶西北3个金矿床为研究对象,使用自编程序绘制每个矿区的赤平投影图,展示各矿区的优势方位,结果符合各矿区的区域地质构造特征。与Dips软件处理结果相比,矿床优势方位误差精度均在±2°以内,验证了所编程序的正确性和实用性。
