油气勘探开发数据体平均值代表性分析

(中国石油辽河油田公司勘探开发研究院，辽宁 盘锦 124010)

0 引 言

油气等各种矿产的勘探、开发、生产等实践中涉及各类数据体(柳炳利等，2016；闫玉茹等，2019)，如物探、钻井、测井等勘探数据，生产、测试、注采等开发数据，岩芯分析、流体分析、热采试验等试验数据，成本、销售、财务等经济数据。如何加以分析运用，如何用于揭示或反映油气藏地质特征、生产规律、经营状况，都是日常面临的问题。统计中平均分析是最常用的数据体定量分析方法。一般来说，平均数(平均值)将同类现象的某一数量标志的各个体数量差异抽象化，用一概括指标综合说明该现象的代表性的典型水平，是最常见、最重要的综合性指标(周兆麟，1989)。在现象的发展过程中，某种共同的必然性因素总是与特殊的偶然性因素交织。为揭示一般的典型特征，需消除偶然性因素的影响，而平均数可抵消或降低偶然性因素变动的影响，最大限度地反映某种客观存在的必然性，因此平均数比个别数值更能反映同类现象的本质。但平均方法不同，平均数也不同(张玉平，2017)，这就必然导致平均值的代表性问题。

目前对确定数据体的典型水平尚无系统性认知和统一的判别标准(郑少智等，2003；姜玉华，2004；邹亚宝，2004；谢忠秋，2006)，同一数据体的典型水平常常不同。对油气藏勘探开发领域常用的数据体平均方法进行对比分析，探讨常用平均方法的适用条件，提出以加权中位数计算公式和平衡中位数法则确定数据体典型水平的方法。

1 数据体平均数种类

1.1 数值平均数

通用表现形式为幂平均数(幂平均值)，数学表达式为：

(1)

1.2 位置平均数

众数指有序数据体中出现频率最高或权重最大的数据，记为Xmo。中位数是将统计数据按升序排列(相同统计数据作为1个数参与排列)，位于有序数据体中间的那一个(组)统计数据的平均值(张玉平，2017；陈文等，2018；何文胜等，2018)，记为Xme或XME。

在油气勘探开发涉及的数据体中，中位数的计算公式一般不考虑加权(周兆麟，1989；张德元，2003；顾永泉等，2018；陈望学等，2020)，仅在图像降噪时会使用加权中值滤波算法(陈家益等，2019，2020)，该算法未在油气勘探开发领域推广应用，也无法诠释加权中位数的全部内涵。加权中位数根据统计数据及其相应频率或权重进行计算：首先计算统计数据按升序排列时的累积频率(或累积权重)，然后确定最接近50%的左累积频率fL(或左累积权重wL)及其左典型数据xL，最后确定统计数据按降序排列时最接近50%的右累积频率fR(或右累积权重wR)及其右典型数据xR。当有序数据体按升序或降序排列时的累积频率(或累积权重)在50%的左侧和右侧的接近程度完全相等且≠50%时，左典型数据和右典型数据均取>50%的最小累积频率(或最小累积权重)对应的统计数据。当每个统计数据(分析数据、观测数据)对应的频数或权数均相等时，加权中位数等于简单中位数。

偏态分布数据体的加权中位数不等于众数。偏态数据体的左累积频率和右累积频率(或左累积权重和右累积权重)及加权中位数的数学表达式为：

(2)

fri=1-fli

(3)

XME=xLfL+xRfR=xLfL+xR(1-fL)

(4)

(5)

wri=1-wli

(6)

XME=xLwL+xRwR=xLwL+xR(1-wL)

(7)

式(2)—式(7)中：fi为有序数据体中第i个(i=1,2,3,…,n)统计数据的频率，f；fli为统计数据按升序排列的第i个(i=1,2,3,…,L；L∈[1,n))左累积频率，f；fL为统计数据按升序排列时最接近50%的左累积频率，统称左特征频率，f；fri为统计数据按降序排列的第i个(i=n,n-1,n-2,…,R；R∈(1,n]；R≥L)右累积频率，f；fR为统计数据按降序排列时最接近50%的右累积频率，统称右特征频率，f；L为数据体按升序排列时第L个(自然数L∈[1,n)；L=1,2,3，…)统计数据；R为数据体按升序排列时第R个(R∈(1,n]；R≥L；R=n，n-1，n-2，…)统计数据；wi为有序数据体中第i个(i=1,2,3,…,n)统计数据的权重，f；wli为统计数据按升序排列的第i个(i=1,2,3,…,L;L∈[1,n))左累积权重，f；wL为统计数据按升序排列时最接近50%的左累积权重，统称左特征权重，f；wri为统计数据按降序排列的第i个(i=n,n-1,n-2,…,R;R∈(1,n];R≥L)右累积权重，f；wR为统计数据按降序排列时最接近50%的右累积权重，统称右特征权重，f；xME为加权中位数；xL为与左特征频率或左特征权重对应的统计数据，统称左典型数据；xR为与右特征频率或右特征权重对应的统计数据，统称右典型数据。

正态分布数据体的加权中位数等于众数，其左累积频率和右累积频率或左累积权重和右累积权重可分别采用式(2)和(3)或式(5)和(6)计算。

2 数据体平均值代表性

2.1 决定因素

对同一组数据体的各种平均值而言，哪种平均值能代表有序数据体的典型水平是数据体分析过程中需要解决的问题，否则会误导对数据体的正确认知。

位置平均数受控于数据体结构，一般不随有序数据体中各具体统计数据(分析数据或观测数据)的变化而改变，是决定数据体典型水平所属区间的指向性数值。

加权中位数作为有序数据体的平衡点，能指示数据体典型水平在有序数据体中的相对位置甚至具体位置。

数值平均数随有序数据体中具体统计数据(分析数据或观测数据)的变化而变化，可确定有序数据体典型水平的具体数值。

综合上述分析表明，平均值的代表性取决于数据体结构和平均值计算方法。

2.2 数据体结构

数据体结构包括数据样本的容量、频数或权数，频率分布曲线或权重分布曲线显现数据体特征。数据体容量越大，数据体特征或统计数据的频率越稳定。数据体权衡指标是否合理，决定了频率分布曲线或权重分布曲线表现出的特征是否客观真实。

统计数据的权重和频率从不同角度评价各统计数据在数据体中代表权的大小，权重越大或频率越高的统计数据表示代表权越大，反之则越小。在实际应用中，权衡指标一般选择统计数据单位或平均值计算公式的分母项(史书良，2006)。若数据体的权衡指标合理，频率分布曲线或权重分布曲线即可客观反映有序数据体的基本特征，例如，孔隙度、渗透率等岩芯分析数据体宜采用储集岩厚度作权衡指标，成本类和价格类数据体宜采用件数(或台数等)作权衡指标，产量类数据体宜采用生产天数作权衡指标，……；若数据体的权衡指标不合理，频率分布曲线或权重分布曲线就无法客观反映有序数据体的基本特征，例如，成本类和价格类数据体不宜采用总金额作权衡指标，产量类数据体不宜采用生产井数作权衡指标，……。对极小值≠0的有序数据体，虽然用权重和频率计算数据体加权平均值的方法(公式)不同，但确定的典型水平可以相同，如成本类、价格类数据体就存在这种情况。

2.3 计算方法

平均值计算方法体现了数值平均数的固有属性，若扣除随机误差和系统误差的影响，简单平均值客观上只与数据体的规模有关，加权平均值还受控于统计数据的频数或权数。同一数据体，从加权算数平均值到加权几何平均值再到加权调和平均值，呈单调递减的特点。在实际应用中，选用哪种数值平均数来代表数据体的典型水平需要借助位置平均数这一标尺，即通过平衡中位数法则来实现。

平衡中位数法则：① 当加权中位数两侧紧邻的自然区间出现≤50%的最大累积频率(或最大累积权重)，或≥50%的最小累积频率(或最小累积权重)时，将区间内有明确物理意义的数值平均数或最靠近加权中位数的数值平均数作为数据体的典型水平或特征平均值；② 在区间内无适合的数值平均数时，加权中位数即代表数据体的典型水平，或用迭代法求取与加权中位数相等的幂平均值作为数据体的典型水平；③ 当有序数据体按升序或降序排列时的累积频率(或累积权重)在左侧和右侧接近50%的程度完全相等且≠50%时，左典型数据和右典型数据均取>50%的累积频率(或累积权重)对应的统计数据。

应用平衡中位数法则确定正常有序数据体典型水平需满足2个条件：① 原始数据体的数据容量足够大，能满足最基本的统计分析要求；② 能选择出合理的权衡指标。

当正常有序数据体的极小值=0时，不能计算调和平均值与几何平均值，此时可令数据体中的极小值=相应数据精度的最小值或1，再根据平衡中位数法则确定数据体的典型水平。若有序数据体的权衡指标选择不合理，加权中位数指示的平衡点即失去指向性，有明确物理意义的加权平均值即为有序数据体典型水平的最佳选择；或可重新确定权衡指标，重新计算加权中位数及数值平均数等。

当有序数据体容量极小，只有2～10个统计数据(分析数据或观测数据)，且众数=中位数时，加权中位数即为数据体的典型水平。当众数≠中位数时，可采用幂平均值公式计算数据体的典型水平，其中阶数k采用左特征频率和右特征频率计算，公式为：

k=fR(1+fL)，|fL-fR|>0.20)

(8)

幂平均值公式中的频数(或权数)可用频率(或权重)替换，则式(1)可简化为：

(9)

或

(10)

经典统计学常采用某一种方法确定或估算数据体的中心位置，正态分布数据体的中位数总能与某一数值平均数相同，偏态分布(非对称分布)数据体中异常值对数值平均数的影响较大，对中位数的影响很小(侯景儒等，1992)。平衡中位数法则以权衡中位数为基础，将多种方法确定的数据体数值平均数与权衡中位数比对，最终确定数据体中心位置(数据体的典型水平)，较传统方法确定的数据体中心位置更客观、合理。

3 实例及分析

对理想情形下的储层物性正态分布有序数据体及权衡指标等参数，用不同方法计算储层物性参数数据体的平均值。例如，孔隙度数据体宜选用储层厚度作权衡指标，其中权数代表相应分析孔隙度的储层厚度。正态分布孔隙度数据体的左特征权重和右特征权重均为50%，左典型数据和右典型数据的平均值等于数据体的众数及加权中位数和算术平均值。根据平衡中位数法则确定加权算数平均值作为孔隙度正态分布数据体的典型水平。

3.1 渗透率平均值代表性的计算

表1为渗透率有序数据体及相应权衡指标等参数，分析用不同方法计算渗透率平均值的代表性。

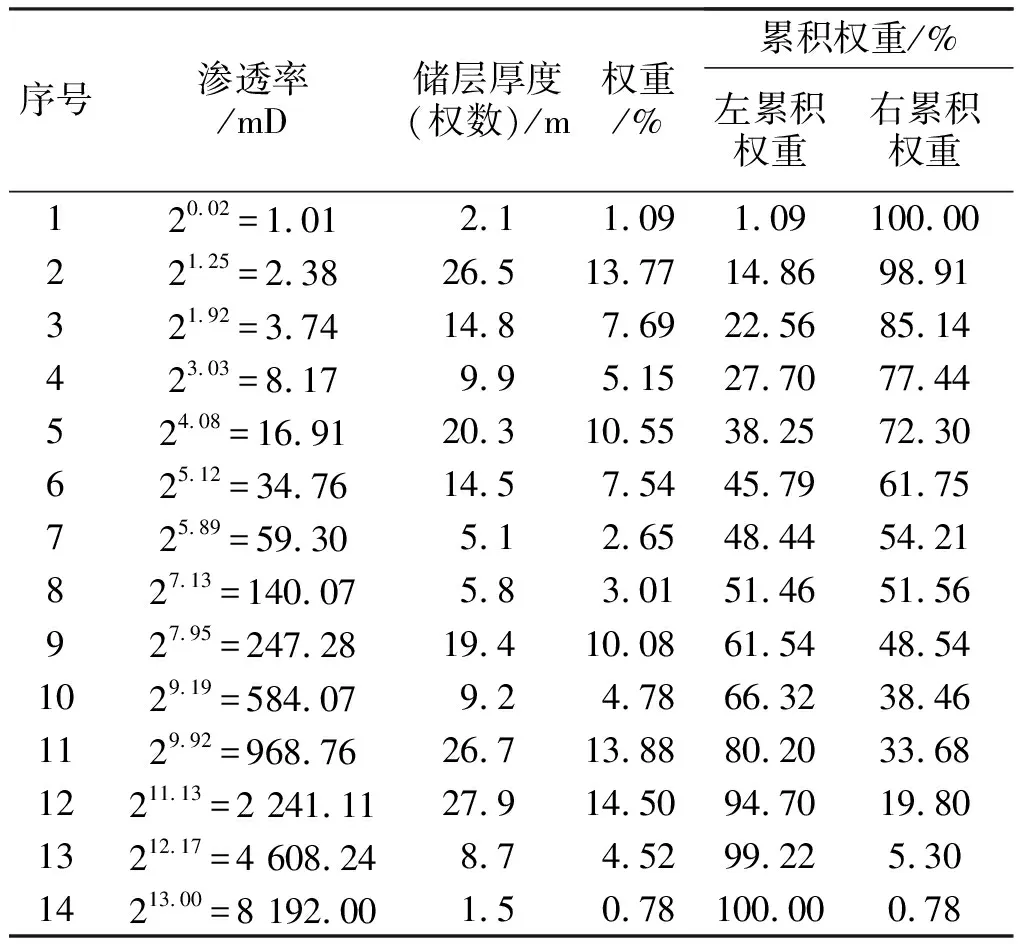
表1 渗透率有序数据体及相应权衡指标参数

对渗透率数据体而言，权衡指标宜选用储层厚度，其中权数代表相应分析渗透率的储层厚度。根据表1,确定渗透率数据体的左特征权重为51.46%,右特征权重为48.54%，则左典型数据为140.07 mD,右典型数据为247.28 mD。渗透率数据体的平均值见表2。

渗透率数据体权重分布曲线(图1)表明渗透率数据体具多峰偏态分布特征。由于渗透率的3种加权平均方法均无明确物理意义，因此采用平衡中位数法则确定渗透率有序数据体的典型水平介于左典型数据和右典型数据之间，即在140.07～247.28 mD之间，在该区间内没有数值平均数落入，故加权中位数190.14 mD即为渗透率数据体的典型水平。随着渗透率数据体的变化，几何平均值会经常入选数据体的典型水平。

图1 渗透率数据体权重分布曲线Fig. 1 Weight distribution curve of permeability data volume

对正常偏态分布的数据体，无论单峰、双峰或多峰，具有明确物理意义的加权平均值是确定正常偏态数据体典型水平的首选。权衡指标的选择也很关键，宜选用观测数据单位的分母项(有明确公式或隐含公式形式)作为权衡指标，当加权平均值公式没有明确物理意义时，选用平衡中位数法则确定数据体典型水平。实际上，具有明确物理意义的加权平均值即可确定正态分布或正常偏态分布数据体的典型水平，绝大多数情况下这2种方法确定的数据体典型水平可相互验证。

3.2 单井平均日产量代表性的计算

某区块单井平均日产量有序数据体及相应权衡指标等参数见表3，分析用不同方法计算数据体平均日产量的代表性。

对单井日产量数据体而言，选用生产天数比生产井数作权衡指标更合理，其中频数代表相应产量的生产天数。根据表3确定产量数据体的左特征频率为58.03%,右特征频率为41.97%，对应左典型数据为7.60 m3/d,右典型数据为15.20 m3/d。单井平均日产量有序数据体的平均值计算结果见表4。

表2 渗透率有序数据体平均值

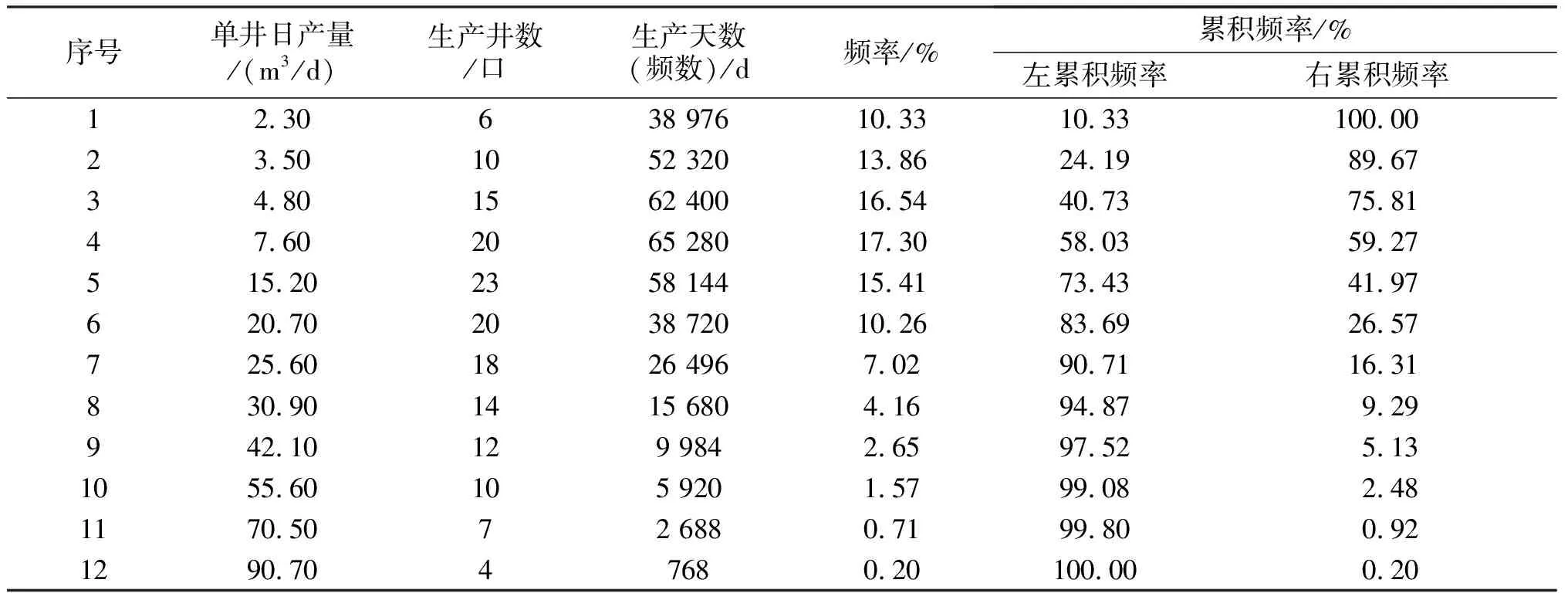
表3 单井日产量有序数据体

表4 单井日产量有序数据体平均值

图2 单井平均日产量数据体频率分布曲线Fig. 2 Frequency distribution curve of average single well daily production data volume

单井日产量数据体频率分布曲线(图2)表明该数据体具单峰偏态分布特征。根据平衡中位数法则，该数据体典型水平介于左典型数据与右典型数据(7.60～15.20 m3/d)之间，虽然加权算术平均值和加权几何平均值均落入该区间，但由于加权算数平均值具有明确的物理意义(总产油量与总生产天数的比值)，因此，加权算数平均值13.05 m3/d为单井平均日产量数据体的典型水平。

采用生产井数作权衡指标确定的单井日产量数据体的典型水平为加权几何平均值16.33 m3/d，没有用生产天数确定的结果客观合理。尽管生产井数不能与生产天数相互转化，但在生产井的信息量有限时，生产井数仍可作为单井平均日产量数据体特征平均值的较为有效的权衡指标。

李映涛等(2015)的研究发现，顺南4井硅化热液的盐度采用几何平均值作为数据体的典型水平较算术平均值更为合理。

4 结 论

(1) 加权中位数是正常有序数据体的平衡点，中位数和众数是分析正常有序数据体典型水平的方向标，加权中位数的计算公式对分析油气勘探开发各领域正常有序数据体的基本特征有指导意义。

(2) 平衡中位数法则是指当加权中位数两侧紧邻的自然区间出现≤50%的最大累积频率(或最大累积权重)或≥50%的最小累积频率(或最小累积权重)时，将区间内有明确物理意义的加权平均值或最靠近加权中位数的加权平均值作为数据体的典型水平或特征平均值；在区间内无适合的数值平均数时，加权中位数即代表正常有序数据体的典型水平。平衡中位数法则适用于正常有序数据体。

(3) 有序数据体的权衡指标一般选择统计数据单位的分母项，否则权重分布曲线不能客观反映数据体的基本特征。当权数与频数可相互转换时，尽管权重分布曲线不能客观反映数据体的基本特征，但采用有明确物理意义的加权平均值仍可确定有序数据体的典型水平。对成本类、价格类、收入类等有序数据体，采用权数或频数确定数据体特征平均值的计算方法有所不同(极小值=0的正常有序数据体除外)。

(4) 对正常有序数据体，采用有明确物理意义的加权平均值与用平衡中位数法则确定的正常有序数据体的典型水平可相互验证。