金属矿山多矿柱承载与失稳破坏研究

朱万成，董航宇，刘溪鸽，牛雷雷，代 风，关 凯

( 东北大学 资源与土木工程学院 岩石破裂与失稳研究所，辽宁 沈阳 110819 )

在金属矿山开采中，当采用房柱法、全面法等 空场采矿法时，会留下许多矿柱来支撑采空区周围岩体，以此维护采场稳定性。矿柱中的高应力集中导致了高应变能的储备，而周围采场的开采活动也提供了能量积聚的外在条件，当载荷超过矿柱的承载极限后，岩体中的弹性能大量释放，将引起多矿柱的大规模失稳破坏。

采空区群是指在一个区域密集分布的大量采空区，如图1[1]所示，其稳定性与多矿柱的承载及失稳破坏密切相关。当采空区体积达到一定规模以至于矿柱不能支撑上覆岩层时，将诱发采空区群失稳和地表沉陷，对矿山生产及地表居民生活造成威胁[2]。采空区灾害是中国分布最广、发生最频繁、危害最大的矿山灾害之一，我国70%～80%的金属矿山存在采空区失稳塌陷灾害，因采矿引起的失稳塌陷面积已达1 150 km2，因采矿诱发失稳塌陷的矿业城市已达30多个，因采空区失稳塌陷造成的直接经济损失达4亿元以上[3-5]。

图1 某金属矿的采空区群[1]Fig. 1 Goaf group of a metal mine[1]

金属矿山的矿柱大规模失稳破坏事故时有发生，往往造成巨大的人员伤亡和财产损失[6]。如，以房柱法开采为主的广东大宝山矿，曾于2004年发生因爆破作业引起的采空区大规模失稳塌陷事故，失稳岩体体积达数千万立方米；南非Witwaterstand金矿共发生千次以上震级达到5级的断层冲击矿压[7]，引起采空区的塌方甚至岩爆。煤矿也有大量采空区失稳案例，如发生在1986年的Lewiston-Stockton煤层的大规模煤柱失稳，仅在8 h内便波及到以失稳煤柱为中心的100 m外的采空区，导致失稳区域顶板下沉超过0.5 m，并伴随着大量支柱的破坏或倾斜。类似的还有2000年发生的Coalburg煤矿大规模煤柱失稳，1998年的Cedar Grove煤矿大规模矿柱失稳和1994年发生的一个磷酸盐矿大规模矿柱失稳[8]。1960年的南非Coalbrook煤矿大规模矿柱失稳造成437人遇难，形成了3 km2的塌陷区[9]。邢台石膏矿矿柱连锁破坏，形成了一个长轴300 m、短轴210 m的椭圆形沉陷区[10]，塌陷总面积达到53 000 m2，塌陷中心最大沉降量约为8.0 m。

另外，围岩体内部赋存有大量的节理、裂隙、结构面和断层等地质非连续面，许多岩石工程的失稳破坏与这些地质非连续面的扩展和贯通密切相关。图2[11]为某矿柱沿结构面发生的失稳滑移破坏。

图2 结构面失稳滑移[11]Fig. 2 Slide instability of pillar along major fracture[11]

因此需要密切关注结构面对矿柱破坏的影响。如果矿柱内赋存了大量结构面，同时岩体内又储存了较高应变能时，一旦矿柱沿结构面发生失稳滑移，会释放大量弹性能，导致顶板断裂和坍塌，严重时甚至造成规模更大的、灾害性更强的多矿柱连锁性失稳破坏灾难。随着浅部资源的逐渐枯竭和对资源能源需求的不断增长，越来越多的采矿活动需要在埋深大、应力高的岩体中进行，岩体失稳破坏灾害的发生频率与等级与日俱增。

由于采空区群主要由矿柱和顶底板这两个基本要素组成，因此许多研究将采空区群简化为多矿柱模型[12]。关于多矿柱承载与失稳破坏特性的研究尚不够完善，多矿柱载荷传递机制尚不清楚，缺乏有效的试验研究和理论分析方法，缺少多矿柱失稳的判据[13]。因此，只有充分研究多矿柱的承载与失稳破坏机制，才能提出更加科学合理的开采方案，进行采空区安全处理和残留矿产资源的高效回收，有效防控大规模采空区失稳破坏灾害，实现矿产资源的安全高效开采。

1 单矿柱稳定性研究方法

地下矿山是复杂的非线性开放系统，矿柱之间以及矿柱与顶底板之间处于相互作用状态[14]，当矿柱与顶底板之间的协同作用减弱时，原有的稳定状态将被打破，将有可能造成大面积的采空区坍塌事故。因此，矿柱稳定性评价是采空区稳定性评价的重要方面。

1.1 单矿柱稳定性评价方法简述

在矿柱稳定性评价方面，具有代表性的分析方法包括安全系数法、力学分析法、突变理论分析法、数值分析法、可靠度分析法和人工智能方法等。

( 1 ) 安全系数法

安全系数法是矿柱稳定性评价的传统方法。安全系数的定义为矿柱强度与矿柱荷载的比值，当比值小于1时，矿柱的荷载超过其峰值强度，即矿柱失效。根据矿柱安全系数的定义建立矿柱的安全系数表达式时，需对矿柱强度、荷载进行估算。

目前预测矿柱强度的方法主要是利用经验公式，并且多数都基于矿柱宽高比[15]。GADDY[16]等首次提出基于试验室测试煤岩试样强度的Holland-Gaddy公式；LUNDER[17]根据现场矿柱的测量和观察进行回归分析推导了一种矿柱强度计算公式；ESTERHUIZEN[18]等通过分析失效矿柱数据库建立了矿柱强度的经验公式，结合Bieniawski岩体分级、室内试验和数值模拟的结果，提出了一种考虑岩石强度、矿柱尺寸和潜在不连续面影响的矿柱设计方法；FANG[19]提出了一个局部退化模型来进行矿柱渐进破坏的平面应变分析及矿柱强度的预测；JAISWAL[20]等通过试验和模拟得出，当矿柱宽高比小于5时，矿柱强度取决于矿柱宽高比，而矿柱峰后应力-应变曲线的非线性则取决于宽高比和单轴抗压强度；MORTAZAVI[21]等研究了矿柱几何形状和矿柱强度之间的关系。

国内外计算矿柱应力的方法主要包括面积分摊法( 如从属面积法、Voronoi图解法 )、数值模拟和梁柱理论模型[22]。丘帆[23]等利用Voronoi图表法估算矿柱所承担上覆顶板的有效面积，进而估算矿柱承载力和稳定性；JAISWAL[24]等运用三维边界元模拟开采过程中的矿柱应力变化，并与实测结果进行对比分析；GHASEMI[25]等分析了矿体分步开挖过程中的应力集中效应，根据矿柱极限荷载、应力状态确定合理的矿柱宽度；POULSEN[22]针对矿柱尺寸和留设位置的随机性，提出荷载传递距离的理念，并通过对工程实例的反演分析验证了模型的可靠性；文献[26]指出矿柱所承担的荷载并不是上覆岩层重力，上覆岩层几乎是以拱桥的形式横跨在矿柱间，且大部分重力转移到附近原岩上，因此从属面积承载理论计算的矿柱安全系数相对保守；罗斌玉[27]等建立了考虑矿体倾角及矿柱受到正应力、剪应力共同作用下安全系数的解析表达式，用于评价任意倾角矿柱的稳定性。传统安全系数法没有考虑矿柱内的应力不均匀性，计算结果偏于保守，而点安全系数法综合考虑了矿柱内的多向应力状态和应力分布的不均匀性。在这方面，点安全系数定义为矿柱内某点可能达到的极限破坏状态值与该点实际的应力状态值之比，综合反映了矿柱整体的强度余量，使计算结果更加接近矿柱的应力-应变实际状态[28]。

( 2 ) 力学分析法

针对矿柱在动力载荷循环作用下的失稳破坏，杨宇江和李元辉[29]将加卸载响应比理论引入矿柱动力稳定性分析中，建立矿柱的加卸载响应比模型，进而确定矿柱的动力稳定性；李江腾[30]基于压杆稳定理论建立了简化的力学模型，计算出高大矿柱的载荷与初始挠度之间的函数关系，从而得出矿柱稳定性的力学判据；POULSEN[22]基于压力拱理论，结合从属面积法计算了房柱法开采时矿柱上的荷载，结果与数值模拟一致；针对缓倾斜层状矿床矿柱的稳定性问题，罗斌玉[31]等根据弹性力学理论分析了缓倾斜层状矿床中矿柱的受力状态，应用图解法绘制出表征矿柱应力状态的广义莫尔圆，结合数值模拟分析了矿体倾角对矿柱强度及稳定性的影响；彭斌[32]等基于矿柱荷载、应力分布和强度，得出某石膏矿山条形矿柱的安全系数，随后根据Bieniawski的面积承载理论和强度计算公式，采用反分析法对矿柱进行了稳定性分析；MA[33]等将顶板视为弹性薄板，将矿柱视为开尔文体，建立大型采空区力学模型；王金安[34]等将顶板视为弹性薄板，将矿柱视为伯格斯体，建立了采空区顶板破坏的流变力学模型。

岩样单轴压缩破坏试验是认识岩体系统突发性动力失稳现象的基础性试验。刚度是岩石力学试验机的一项重要性能指标，其大小对岩石单轴压缩试验的结果有很大影响，将单位载荷作用下试验机整体框架所发生的变形定义为试验机的刚度。COOK[35]通过大量试验分析后提出岩样失稳破裂的条件为km＜|f′(ut)|，即Cook刚度判据，km为试验机刚度；ut为曲线峰后软化阶段的拐点。当f′(ut)+km＞0时相当于刚性试验机加载，则试样不会发生失稳；当f′(ut)+km＜0时相当于柔性试验机加载，则试样会发生失稳。如图3所示，岩样失稳破裂发生在f′(ut)+km=0的uA处，而不是在峰值载荷点。其中，u为岩石试样的形变；f(u) 为岩样本构关系，即荷载-形变全过程曲线的表达式；A为岩样失稳的起始点；f′(uA)为曲线A点处的斜率；B为岩样失稳的结束点。在采矿工程实践中，可以把矿柱视为单轴压缩试验中的试样，而围岩对矿柱施加载荷，可以认为是试验机，因此，矿山岩体的刚度是影响矿柱剧烈破坏行为的重要因素。如果围岩体的刚度相对于矿柱“较软”，那么矿柱屈服时围岩释放的能量将大于矿柱所吸收的能量，从而发生矿柱失稳。

图3 柔性和刚性加载条件Fig. 3 Soft and stiff loading condition

利用相互作用的两体力学模型可以较好地揭示岩石失稳的物理本质。CHEN[36]等通过双岩石试样串联的方式，建立两体相互作用模型来研究岩石试样的失稳破坏行为，当串联试样中最弱试样发生破坏时，相邻试样将发生回弹并引发串联试样的失稳破坏；尤明庆[37]建立了岩石试样与试验机的相互作用模型，将试样看作弹簧和楔块两种元件的组合。楔块表征岩石的塑性变形和弱化，并提出弱化模量的概念来表征试样的峰后力学特性。基于该模型，推导了岩石试样-试验机系统的失稳破坏准则。当试样的长径比大于3时，试样接近脆性破坏，此时，试样自身的弹性应变的释放就可以引起试样的失稳破坏，而不需要试验机再施加额外载荷。因此，当矿柱的高宽比达到一定值以上时，矿柱的刚度降低，即使围岩体刚度比较大，矿柱也有可能会发生失稳破坏[38]。SALAMON[39]提出矿山局部刚度Local Mine Stiffness( LMS )的概念，定义了不同开采阶段特定区域内围岩体的等效刚度[39]，描述了上下盘或顶底板之间的荷载-变形特征。在评估矿山结构( 如多矿柱或采空区群系统 )的稳定性和冲击倾向性时[40]，可以使用该等效刚度来确定局部矿山结构的刚度。如果LMS小于矿柱峰后刚度的绝对值，则会引起矿柱结构的失稳破坏[41]。

( 3 ) 突变理论分析法

突变理论( Catastrophe Theory )最初由THOM[42]提出，经TROTMAN[43]，ZEEMAN[44-45]和POSTON[46]等扩充完善，旨在研究自然界中不连续或跳跃性的现象。突变是指系统演化过程中，某些变量的连续变化导致系统状态的突变，即系统从一种稳态跳跃到一种新的稳态。突变理论是研究非连续现象的一个数学分支，是在拓扑学、奇点理论、结构稳定性等数学分支的基础上发展起来的，特别适用于描述自然界中作用力或动力的渐变导致状态突然变化的情况，这也是其被称为突变理论的原因[46]。

唐春安[47]在《岩石破裂过程中的灾变》一书中，基于突变理论中的尖点灾变模型与损伤力学原理，分析了岩石单轴压缩过程的失稳破坏现象，导出了岩石失稳破坏准则、能量、突跳值等数学解析表达式，从而使岩石真实的失稳破裂过程得到更多地关注，而非人为控制下的岩石稳定破坏过程。随后尖点突变模型被广大学者用于矿柱失稳、滑坡、断层失稳滑移、地震、顶板冒落、巷道岩爆、煤与瓦斯突出等各种灾害的机理研究中，并取得了丰硕的研究成果[48-57]。徐曾和[49]等建立了顶板与煤柱组合的力学模型，并基于尖点突变理论分析了煤柱岩爆的失稳破坏稳定机制，推导了煤柱-顶底板系统的失稳准则、顶板突跳和能量释放表达式，并研究了矿柱岩爆的前兆规律和信息。LI和CAO[51]通过建立矿柱-顶底板系统的非对称开采物理模型，从整体上讨论了系统的失稳问题，并导出了矿柱位移突跳值与能量释放的表达式。为了进一步弄清矿柱-顶底板系统的失稳破坏机制，还有学者将力学模型与突变理论相结合，如将两体相互作用模型与突变理论结合[58-60]，对实验室岩样失稳破坏的能量、失稳判据进行定量描述等。WANG[52]等建立了两体力学模型，用两种材质分别模拟顶底板和矿柱，通过数值模拟和理论分析相结合的方法，揭示了矿柱的失稳破坏机制，认为岩石系统的稳定性特征是由系统内各部分的刚度分布决定的。同样的，QIN[53]等基于突变理论研究了顶底板和煤柱组成的力学系统的失稳机理，发现导致失稳的因素主要是煤柱与顶板的刚度比；付成华和陈胜宏[61]利用突变理论从不同判据出发探讨了硐室围岩的失稳问题；张钦礼[62]等建立了采场矿柱-顶板简化力学模型，基于尖点突变理论从能量释放角度分析了采场矿柱-顶板系统的稳定性，认为矿柱的应变软化特性和刚度比是导致失稳的主要因素；陈庆发[63]等以突变理论为理论支撑，建立了采空区顶板-矿柱的协同作用力学模型，研究了矿柱、顶板结构参数的改变对采空区协同效应的影响；LIU[64]等建立了矿柱和顶板相互作用的力学模型，并基于板的弯曲理论和突变理论，分析了矿柱-顶板系统的协同失稳行为，同时给出了矿柱-顶板系统发生破坏和整体失稳的力学条件和数学判据。针对房柱法开采下的石膏矿稳定性分析，XIA[65]等根据现场调查建立了矿柱-顶板系统简化力学模型和石膏矿柱-顶板系统的尖点突变模型；夏开宗[66]等针对石膏矿矿柱-顶板支撑体系的破坏特征，构建石膏矿矿柱-顶板支撑体系突发破坏的尖点突变模型，分析了支撑体系的几何参数对采空区稳定性的影响；高明仕[67]等将顶板和矿柱均视为弹性体，建立了煤柱失稳冲击破坏的尖点突变模型；贺广零[68]等将顶板视为弹性薄板，将矿柱视为温克尔弹性地基，建立了采空区煤柱-顶板系统失稳的尖点突变模型。这些基于突变理论的模型研究，为认识矿柱的失稳破坏机理提供了重要理论依据。

( 4 ) 数值分析法

数值分析法被广泛地应用于矿柱稳定性评价中[21,69-72]。LI[69]等利用FLAC3D建立某海底金矿三维数值模型，综合分析了海水压力和开采顺序对顶柱稳定性的影响；DEHGHAN[70]等通过数值模拟的方法研究了一个多矿柱多米诺失稳破坏案例，模拟了载荷传递与破坏过程。由于实际工程中，矿柱内往往赋存着许多大小产状不等的结构面，ELMO和STEAD[72]通过将离散元和有限元相结合的方法，模拟了结构面对不同宽度矿柱稳定性的影响；AKSOY和ONARGAN[71]根据土耳其某采石场的地质构造和岩石物理力学性质等现场数据，通过数值模拟确定了开采的房柱最佳参数，估算了矿柱中的垂直应力，并进行了多矿柱系统的稳定性分析；赵奎和蔡美峰[73]通过三维有限元数值分析方法，确定了回采区优势结构面、关键矿柱以及矿柱临近区域的损伤情况，对残留矿柱回采方案进行了稳定性分析；郭建军[74]应用突变理论和数值模拟相结合的方法，对某金矿的矿柱进行了稳定性分析，并分析了开采扰动对矿柱稳定性的影响。针对浅部与深部过渡区域隔离矿柱的设计问题，赵兴东[75]采用极限跨度法、经验公式法以及极限平衡分析方法，计算出合理的隔离矿柱厚度，随后利用FLAC3D对隔离矿柱的稳定性进行了模拟分析。由于矿柱的峰后力学特性与矿柱的破坏形式有着密切的关系[76]，可以根据断裂和损伤力学原理建立力学模型，来描述材料的峰后力学行为。IANNACCHIONE[77]，WHYATT和BOARD[78]在有限差分分析中使用应变软化模型来探索矿柱的峰后软化行为；MARTIN和MAYBEE[79]在有限元分析中采用脆性参数来预测岩柱的峰后力学行为；DUNCAN[80]和ADHIKARY[81]等在有限差分和有限元分析中使用应变软化模型来研究矿柱的峰后特性；MORTAZAVI[21]等使用有限差分法和应变软化模型来捕捉硬岩矿柱的失稳破坏行为；ELMO和STEAD[72]使用有限元和离散元耦合的方法对矿柱内的裂隙网络进行显式建模；李夕兵[82]等采用FLAC3D对深部开采矿柱进行高应力下动力扰动数值计算，分别分析了不同静载以及不同动力扰动影响下的矿柱稳定性。基于矿柱多维剪切破坏的特征，王在泉和李华峰[83]提出了矿柱抗剪安全系数的概念，采用有限元强度折减法计算了矿柱的抗剪安全系数，并与传统方法所得安全系数进行对比分析；赵奎[73]等对某金矿残留矿柱回采方案进行了三维有限元数值分析，并提出了合理的矿柱支护方案。

( 5 ) 可靠度分析法和人工智能方法

可靠度的研究起源于20世纪30年代，被广泛应用于铁路、公路和水利等各类工程领域。刘学增[84]等针对矿柱设计中传统的安全系数法，在忽略岩体固有的节理、裂隙特性的影响的条件下提出了可靠度设计法；周子龙[85]等基于可靠度分析法，综合考虑多矿柱的整体承载能力和承担的总载荷，建立了多矿柱的结构功能函数，用来评价多矿柱的稳定性；NAJAFI[86]等运用一次二阶矩和高次二阶矩可靠度分析方法对矿柱的稳定性进行了分析；刘沐宇[28]等考虑岩体性质的变异性和随机性，采用蒙特卡洛法对矿柱结构可靠度进行了分析与计算；GRIFFITHS[87]基于蒙特卡洛模拟方法，运用随机场理论和弹塑性有限元算法分析了地下矿柱的稳定性；WATTIMENA[88-89]等根据矿柱表观数据，将矿柱划分为稳定和失效2种类型，利用二元逻辑回归模型计算了矿柱稳定的概率，并 将其划分为稳定 ﹑不稳定和失效等3种类型，同时利用多元逻辑回归模型预测硬岩矿柱的稳定性；刘沐宇[90]等运用点安全系数法和可靠度分析法分别计算了矿柱的点安全系数和可靠度指标，此方法把安全系数的计算推广到二维或三维受力状态，使安全系数的计算包含了强度准则的内容。

矿柱的稳定性评价是一个涉及多层次、多指标的系统工程，且影响因素之间存在诸多模糊信息，从而使矿柱的失稳具有未知性和随机性，人工智能方法不同于传统方法，可以将复杂问题中的各影响因素之间进行层次排序，并利用数学的方法确定各层次影响因素的影响权重，从而给出一个矿柱稳定性的综合判断。人工智能法包括费舍尔判别法( Fisher Discriminant Analysis，FDA )、支持向量机( Support Vector Machine，SVM )、模糊综合评价法( Fuzzy Comprehensive Evaluation，FCE )、人工神经网络( Artificial Neural Network，ANN )等方法。费舍尔判别法( FDA )是一种基于统计学理论的，具有代表性的线性方法。郝先虎[91]基于Fisher判别分析法，建立了包含矿柱尺寸、应力、岩石单轴抗压强度等因素在内的矿柱稳定性预测模型，可以较好地对矿柱稳定性进行预测和评估。支持向量机( SVM )是SAIN[92]在统计学理论基础上发展起来的一种有效的机器学习方法，是一种具有代表性的非线性方法；ZHOU[93]等应用支持向量机法建立了矿柱稳定性预测模型，并利用矿山实测数据对模型进行了训练和测试( 包括矿柱尺寸、岩石单轴抗压强度和矿柱应力等 )，结果表明支持向量机是一种可靠、实用的地下矿山矿柱稳定性评价工具。模糊综合评价法( FCE )是将层次分析法和模糊数学相结合的一种综合评价方法，适合于多层次、多指标、多方案的优化决策问题。张睿和刘涛[94]采用模糊综合评价法对房柱法矿柱的结构参数进行了优化研究；TAWADROUS[95]利用人工神经网络( ANN )方法来预测矿柱的稳定性；IDRIS[96]等利用神经网络模型，结合矿柱所能承受的最大应变，从可靠性指标和失效概率两个方面对矿柱的稳定性进行了评估。

这些矿柱稳定性人工智能分析方法各有优劣，Fisher判别法算法简单且具有较好的鲁棒性，对确定性和随机性模式的分类都适用，可以抓住关键样本、剔除冗余样本。支持向量机方法的优势在于通过分界面能够直观地表现类别间的区分，但其缺点在于只能用于具有明显差异的小样本间的区分，误差较大。综合评价法根据模糊数学的隶属度理论把定性评价转化为定量评价，因此具有结果清晰、系统性强的特点，能较好地解决模糊的、难以量化的问题。神经网络算法对不确定的问题有自适应和自学习能力，能高精度地逼近连续的非线性函数，很好地协调多种输入信息的关系；然而人工神经网络存在学习率不稳定，容易陷入局部最优的缺点，这使得预测结果偏离了工程实际情况。

综上所述，上述单矿柱稳定性评价方法有如下优缺点：安全系数法简单实用，广泛用于工程实际；但是没有考虑矿柱内的应力不均匀性，计算结果有时与实际情况偏差较大。力学分析法可以较好地揭示岩石失稳的物理本质，但有些模型存在过于简化，而另外一些模型则存在参数过多且物理意义不明确的缺点。突变理论分析则抓住了矿柱失稳的本质，但工程问题往往难以简化为可以用突变理论表达的模型，获得的结果具有很大的局限性。数值模拟方法的优点在于能够考虑更为复杂的地应力场、开采过程等边界条件，也能够采用更为复杂的岩石力学本构关系；但是，由于数值模型实际上难以完全与工程实际相一致，很多情况下数值预测结果的准确度也值得商榷。可靠度分析法不需要关心系统内部构造，既可以定性分析又能定量分析，因果关系清晰且形象，但忽视了系统内部的作用关系，且相关数据难以获取。人工智能方法的优点是可以在不关心矿柱破坏过程力学机理的基础上做出有效的预测分析，但由于岩体工程样本数量有限，矿柱的破坏共性特征不明显，这使得预测结果存在很大的不确定性。

1.2 结构面对矿柱稳定性的影响

在实际工程中，工程岩体以及矿柱内部往往分布有许多大小、产状不等的结构面[97]，较大的结构面甚至贯穿整个矿柱，其极大地降低了矿柱的承载能力，改变了矿柱岩体的力学及变形特性。由于多矿柱-顶底板系统的失稳破坏与结构面的扩展、分叉和贯通密切相关，因此研究岩石结构面的失稳滑移行为具有重要的理论和实际意义。早在1960年，JAEGER[98]就基于Mohr-Coulomb准则提出了含单条贯通性结构面试样的强度解析解，如果试样含多组贯通结构面，其强度的确定方法是分步运用单结构面理论，分别绘出每一组结构面单独存在时的强度包络线和应力莫尔圆，岩体总沿着强度最小的那组结构面破坏，岩体强度为该组结构面强度[99]。

在室内试验[100-106]、数值模拟[107-108]以及理论分析[109-111]方面，国内外很多学者开展了结构面对矿柱稳定性影响的研究。杨圣奇[105]等利用3D打印和混凝土浇筑的方式制作含贯通粗糙节理的人工岩石节理试样，随后进行不同围压下常规三轴压缩试验，研究结果表明，随着JRC( Joint Roughness Coefficient )的增大，岩石试样由脆性破坏转变为延性破坏；ZHANG[107]等利用Synthetic Rock Mass ( SRM )方法和PFC3D研究了成组节理对矿柱的影响，结果表明，与无节理矿柱相比，含成组节理的矿柱的峰值强度和变形模量分别降低了68.1%和44.8%；SINHA和WALTON[112]采用黏结块体模型( Bonded Block Models，BBM )模拟了硬岩矿柱的渐进损伤过程，并研究了锚杆加固对矿柱强度和变形能力的影响；MUAKA[113]等基于Voronoi方法和UDEC2D开发了一种含大量节理的硬岩矿柱的设计方法；FARAHMAND[114]等采用离散断裂网络( DFNs )和离散单元模型( DEM )研究了含中等节理岩体在不同约束条件下的力学特性，利用代表单元体( REV )研究了岩体的尺度相关性，并将数值结果与经验方法的估计值进行比较；ZHANG和ZHAO[115]基于SRM方法和PFC3D对含大量节理矿柱的约束效应进行了数值模拟研究，发现围压将导致更高的矿柱强度和延性，当矿柱在一个横向方向受到高应力限制，而在另一个横向方向受到零或低应力限制时，可模拟出更加脆性的峰后行为；郭松峰[116-117]等利用FLAC3D对含贯通结构面试样的单轴压缩特性进行了数值模拟研究，考虑了结构面倾角、组数以及粗糙度的影响，认为试样的渐进破坏行为可分为塑性滑移破坏、滑移-剪切脆性破坏、剪切脆性破坏和塑性剪切破坏等4种破坏模式；郑青松[118]等研究了单轴和三轴载荷条件下结构面倾角对岩样力学特性的影响，对Jeager单结构面判据进行了修正；冒海军和杨春和[119]基于Jeager单结构面理论，建立了含贯通结构面试样的一维和三维抗压强度预测公式；李宏哲[120]等开展了含天然节理大理岩试件的常规三轴压缩试验，发现了穿切节理面破坏和沿节理面滑移两种破坏形式。

结构面的剪切滑移成为矿柱破坏的主要形式之一。在这方面，目前学者们关注最多的是结构面抗剪强度、粗糙度表征、尺度效应、本构模型以及其他结构面剪切特性( 如声发射特性、渗流及力学耦合特性 )等方面的研究[102,121-129]。当结构面的粗糙度以及应力状态满足一定条件时，结构面的剪切破坏过程将表现出失稳滑移现象[130-131]。DONG[130]等研究了岩石结构面在不同法向载荷下的剪切失稳特性，以峰后跌落斜率ksa描述结构面峰后软化行为，发现跌落斜率ksa随法向载荷的增加呈指数或线性增加的关系；唐志成[132]等提出以双曲线形式描述结构面峰值剪切强度后的应力- 位移曲线关系；USEFZADEH[123]等认为，峰后阶段大量微凸体发生剪断，结构面粗糙度逐渐退化，并基于Goodman模型提出了描述峰前和峰后两个阶段的非线性模型；唐志成[122]等认为，在结构面剪切过程中，当微凸体爬坡效应占主导地位时，表现为剪切硬化；当微凸体磨损累积到一定程度时，表现为剪切软化。

在结构面滑移的本构模型研究方面，王水林[133]等对结构面剪切应力-位移曲线峰后软化阶段的特性研究进行了简单的综述，将结构面本构模型分为全量型和增量型。全量型结构面本构模型分为连续型和分段型，主要依据试验测试曲线，采用基本的数学函数来拟合不同阶段的试验曲线。增量型结构面本构曲线是以弹塑性理论为基础，结构面剪切应力与剪切位移可以假设为理想弹塑性关系，增量型本构模型更适合于工程岩体变形过程的分析。

在全量型结构面本构模型研究过程中，GOODMAN[134]为较早研究结构面本构关系的学者，他将结构面非线性变形归结为结构面面壁微凸体的非线性压碎与剪断，提出类似于广义Hook定律的弹性本构关系；SAEB[135]等继Goodman模型之后提出纯线性的分段函数模型，但不能描述结构面的非线性力学行为；PARK[136]等做了362个结构面直剪试验，据此提出描述峰值摩擦因数和法向变形特征的经验型本构模型；POUYA[137]等提出岩石结构面的弹塑性变形和损伤过程模型，该黏结损伤模型( Cohesive-Crack Model )较好地反映了结构面的损伤破坏过程。为了评估结构面峰后剪切刚度，SIMON[138]于1999 年提出了CSDS( Complete Stress-Displacement Surface Model )模型，该模型包含2个指数型函数，分别表示摩擦和微凸体剪切破坏，但是CSDS模型参数计算复杂，有时难以得出显式解；AMADEI[139]等提出采用双曲线函数描述峰前的剪切应力-位移关系，但是对峰值后部分仍然采用线性函数；GRASSELLI[140]等采用线性函数拟合峰前部分，采用双曲线函数拟合峰值后部分，双曲线的形态由峰值强度、残余强度及剪切位移确定。在增量型本构模型研究过程中，PLESHA[141]基于非关联流动法则研究了不连续面的弹塑性本构关系，采用塑性功指数衰减函数表示剪胀角的演化过程；徐磊和任青文[142]将结构面切向和法向变形分为峰前线性段、峰前非线性段和峰后软化段，其中峰前线性段采用弹性模型，峰前非线性段采用抛物线函数，峰后软化段采用软化函数；方理刚[143]假设结构面滑动为塑性变形，提出了遵循非关联、弹塑性耦合流动法则的增量型弹塑性本构关系表达式。

综上可知，物理试验是研究结构面影响下单矿柱承载能力与失稳机理的重要手段，由此可以直观地观察到矿柱的裂纹产生、扩展、聚集和贯通现象，同时，因其边界条件简单，也便于相关学者建立理论模型。数值计算方法可以避免物理试验中遇到的加载能力不足、测量范围有限等问题，具有通用性强、方便灵活、可重复性等特点，虽然数值方法也存在岩体本构关系、边界条件设置的难点问题，但日益受到学者们的重视，新的模型和算法仍然是未来的研究重点。

2 多矿柱相互作用稳定性研究

目前国内外主要研究了单矿柱-顶底板组成系统的失稳破坏机制；而对多矿柱的动态失稳过程和发生机制的研究较少。多矿柱应力状态复杂，每一个矿柱的变形破坏都会打破原有的受力平衡，使相邻的矿柱产生损伤和应力重分布。经过多次应力重分布，围岩的应力状态将变得极其复杂。在实际生产中，开采活动往往是连续进行的，新的采空区和矿柱形成时，前一个应力重分布过程可能尚未完成，导致围岩的应力状态复杂多变。房柱法开采后往往留下许多不同尺寸和形状的矿柱作为临时或永久支护，这些矿柱与周围岩体共同作用，保证了地下采场的稳定[144-145]。

地下矿山经过长期开采而形成的采空区群围岩稳定性较差，容易引起采空区群系统大规模失稳破坏的“群效应”事故[146]。对多矿柱系统而言，当其中某一个矿柱体失稳破坏后，原先作用在该矿柱上的载荷将传递到相邻矿柱上，极有可能会导致多矿柱大规模失稳破坏。在该情况下，关键矿柱失稳破坏造成的载荷传递行为( 或者说是应力转移行为 )往往会引起一系列的连锁性反应，当转移的载荷超过相邻矿柱的承载极限时，可能会引发矿井大面积的坍塌[147-150]。随着开采深度的增加，多矿柱的连锁失稳破坏现象逐渐显现，关键矿柱的失稳破坏可能引起大范围内多矿柱失稳破坏，除了突然性、影响范围大等特点外，还具有扰动和诱发“多米诺效应”的特点[151-152]。

SWANSON和BOLER[153]提出“Cascading Pillar Failure( CPF )”这一术语来描述多矿柱的连锁失稳破坏行为。房柱法开采过程中出现的连锁性矿柱失稳破坏现象也称为“Progressive Pillar Failure”、“Massive Roof Collapse”、“Domino-type Failure”或“Pillar Run”[152]。矿柱可能以不同的方式发生破坏，这取决于矿柱的力学特性、采场布置、围岩结构特征和地应力状态等因素。在某些情况下，只有邻近几个矿柱受到影响而发生破坏；然而，在极端情况下，数十个甚至数百个矿柱可能发生多米诺式的连锁破坏现象。如，Fetr6铬矿的残余矿柱破坏导致4 000 m2范围内的矿柱在几分钟内发生破坏[70]。2015年，美国宾夕法尼亚州西南部一个石灰石矿约35根矿柱突然坍塌，波及30 000 m2的地下区域[154]。另据报道，美国煤矿和非金属矿山在20世纪90年代分别发生了至少8次和5次此类多矿柱连锁失稳破坏事故[152]。

国内外学者对矿柱失稳破坏的研究多集中于单个矿柱本身的承载能力或者失稳过程，而对于多矿柱间的载荷传递及“多米诺效应”的研究相对较少[148-150]。MA[33]等研究了多矿柱发生大规模坍塌的“多米诺效应”，认为引起“多米诺效应”的物理本质是上覆岩层的载荷重分布效应，如图4所示。采空区群系统形成初期，受到地质结构面切割的顶板会发生局部冒落，形成自然平衡拱，并保持长期稳定状态。随着时间的推移，矿柱在顶板荷载作用下发生缓慢蠕变，当损伤发展到核部承载区后，矿柱失稳，不再承担顶板荷载。随后，失去矿柱支撑的顶板会发生局部冒落，再次形成新的应力拱，将荷载转移到周边矿柱。周边矿柱荷载增加后，可能进一步失稳，从而顶板应力继续向外转移，最终当足够多的矿柱发生失稳，裂隙发育带到达地表后，将发生地表大面积瞬时切冒型塌陷。这种由局部矿柱破坏引发的顶板荷载传递和矿柱连锁式破坏并最终导致大面积塌陷灾害的现象，称为采空区塌陷的“多米诺效应”[155]。李俊平[156]将坚硬顶板下采空区多矿柱的多米诺骨牌式失稳过程称为顶板冲击地压；LI[157]等则尝试从多矿柱能量传递的角度出发解释“多米诺”失稳的机理。随着国家对采空区治理力度的加大，采空区群失稳破坏行为，特别是多矿柱体系的载荷传递行为诱发的采空区破裂行为，逐渐受到重视[158-162]。

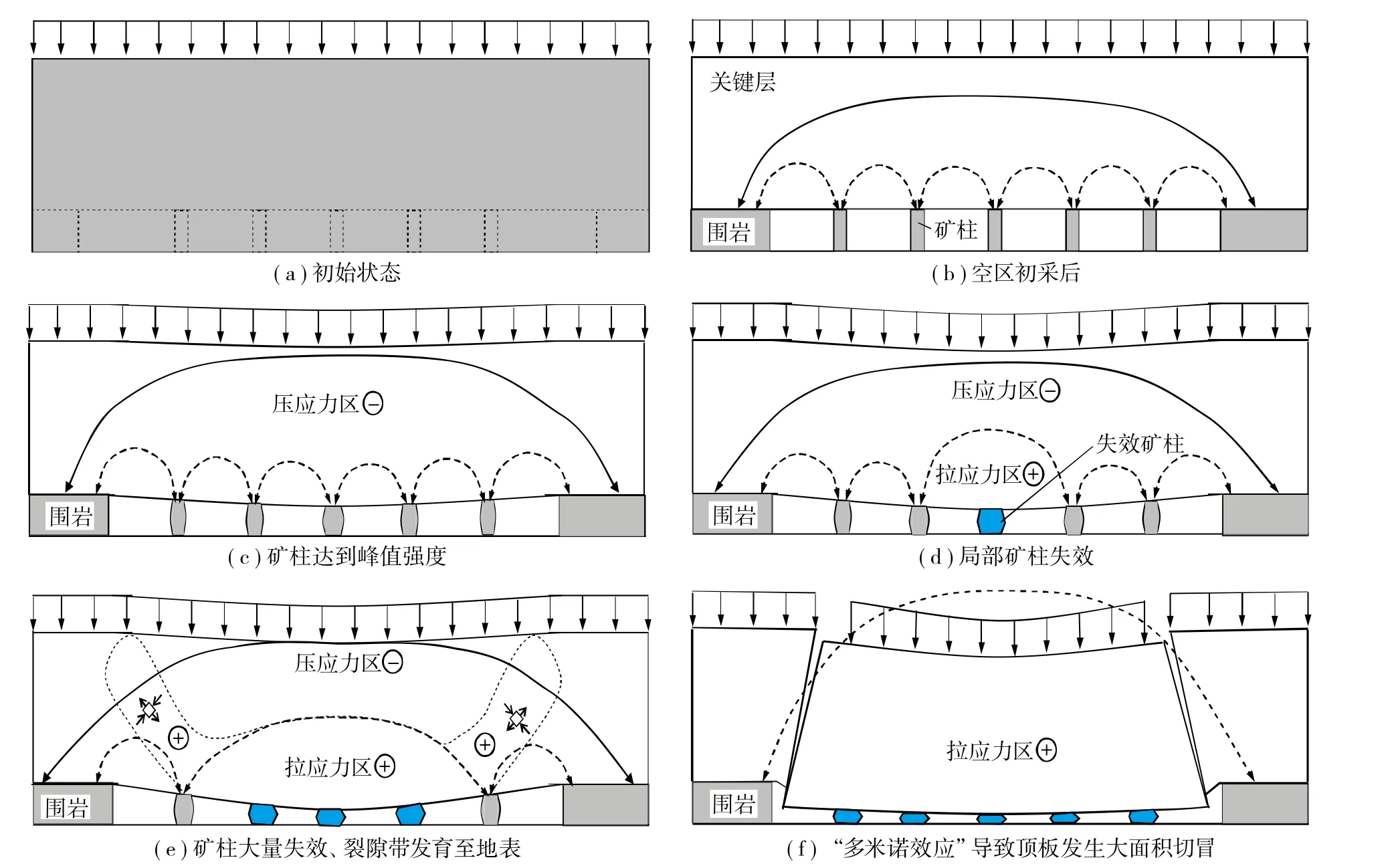
图4 多矿柱失稳破坏的“多米诺效应”[33]Fig. 4 Domino effect of pillar group instability

2.1 多矿柱载荷传递力学模型

目前国内外学者主要采用理论分析[163-165]、数值模拟[166]、室内试验[167]和现场监测[168-169]等方法对采空区群系统的稳定性进行研究。此外，重整化群方法[170]和局部刚度理论[171]也被用于多矿柱的稳定性问题研究。

由于采空区群系统的稳定性主要由顶底板和矿柱这2个基本要素决定，所以许多研究中将采空区简化为矿柱-顶底板系统模型[12]。如，一些学者将顶板、矿柱、约束、连接方式等进行适当简化，基于结构力学构建了采空区群类框架结构模型[172-173]，以类框架结构模型为分析基础，建立了顶板、矿柱及采空区群安全系数表达式，获取了采空区群各影响因素的重要度排序、主控因素及相应的临界值，评价了采空区群的稳定性。ZHOU[174]等通过建立基于压力拱理论和结构动力学的力学模型，研究了多矿柱体系下残余矿柱回采瞬间的卸荷作用引起的连锁反应，发现残矿回采所引发的卸荷效应是引起多矿柱大规模失稳坍塌事故的诱因。基于以上对多矿柱载荷传递行为的研究，载荷传递机制或物理本质成为学者们感兴趣的研究点；POULSEN[171]对矿柱失稳过程中的载荷转移规律进行了定量假设，并用数学方法对多矿柱连锁失稳的风险进行了定量评估，引入概率方法预测了多矿柱连锁失稳的概率；柯昌涛[175]等研究了矿柱失稳后的荷载重分布规律，研究了采空区多矿柱的连锁倒塌机制；赵源[174,176]等则研究了不同开采强度条件下房柱法采空区连续倒塌灾害动力诱发机制，初步探讨了应力重分配对相邻矿柱的连续动力过载作用。由于载荷传递效应的存在，使得采空区群系统的失稳破坏有别于单个采空区[177]。

此外，矿柱的荷载传递和倒塌不仅与矿柱本身的力学性质有关，还受围岩刚度的较大影响[178-180]。STARFIELD和FAIRHURST[181]提出了可以估算单一矿柱所在地层的刚度理论，该理论认为矿柱在理论上可假设为液压千斤顶，当千斤顶回缩时，可以绘制出千斤顶支撑区域顶底板相对位移随千斤顶载荷变化的曲线，该载荷-位移曲线的斜率，即矿柱所在地层的局部刚度。由于复杂的围岩地质条件，如何正确估算矿山岩体的局部刚度( LMS )成为学者们所面临的最大挑战，并且可参考的相关研究案例也比较有限。但是，在数值模拟方法的帮助下，可以通过建立地质模型来计算特定条件下的LMS，例如图5所示展示了利用边界元法确定局部刚度的方法[182]，其中矿山岩体的局部刚度LMS可通过公式KLMS=f1/(d2-d1)进行估算，其中，d1和d2分别为有矿柱和无矿柱时围岩体的收敛情况；f1为多矿柱承受的荷载，f2=0。

图5 利用边界元法确定矿山局部刚度LMS[182]Fig. 5 Procedure for determination of local mine stiffness by BEM simulation[182]

基于这种方法，许多学者采用不同的数值模拟工具计算了LMS[183]。如，ZIPF[184]使用非连续模型计算了LMS，并提出LMS与顶底板岩体的杨氏模量之间的线性关系；KIAS[185]采用FLAC-PFC耦合方法研究了矿柱高宽比对LMS和峰后特性的影响，结果表明，LMS随着加载系统杨氏模量的增加而呈现降低的趋势。由于可以借助数值模拟手段来计算LMS，使得利用SALAMON的LMS准则来评价矿山结构的失稳倾向性以及矿山设计也成为可能。GU和OZBAY[186]在UDEC中利用LMS准则来区分稳定和非稳定滑动破坏。通过分析发现随着采矿活动的进行，LMS逐渐降低，因此岩体结构发生失稳破坏的可能性也随之增加；ADHIKARY[81]等利用LMS准则与安全系数对高壁开采盘区的稳定性进行了数值研究，为盘区的布局设计提供参考；LACHENICHT[187]研究了LMS与微震事件之间的相关性，并提出了针对具有岩爆倾向矿山的矿井设计方案。

研究重点与展望：载荷传递的物理本质在于矿柱之间以及矿柱与围岩体之间的相互作用，多矿柱支撑体系中某一个或几个矿柱破坏后，由于力的传递将造成相邻矿柱的连锁性失稳及大规模坍塌灾害的发生。目前，这种相互作用下引起的荷载传递机制尚未揭示清楚，未来研究将更加关注围岩体的弹性储能与释放的定量化分析工作。理论模型考虑的因素有限，需要对研究对象进行简化，因此难以反映工程问题的实际边界条件。由于工程问题的边界条件复杂多变，如果针对每个工程问题建立独立的理论模型进行简化和建模分析，往往会增加工作量，且计算结果不一定适用。相对地，利用数值模拟并结合工程实际工况建立复杂的模型，有利于更加真实地反映现场实际，将在未来发挥越来越重要的作用。

2.2 多矿柱载荷传递试验

研究简单的双矿柱体系的承载与失稳破坏特性，对理清矿柱间的协同作用机制以及理解多矿柱的承载与失稳破坏特性具有重要的作用。目前常见的多矿柱物理试验模型主要分为“整体式”[188]和“分体式”[189]两种，具体形式如图6所示。

图6 双矿柱物理试验模型及其试验系统Fig. 6 Double-pillar model and test system

XU Shuai[188]等采用整体式双矿柱体系模型，利用声发射检测技术，记录了整体式双矿柱体系模型的变形破坏过程的声发射信息，描述了模型中裂纹的萌生和扩展特性。周子龙[189]等采用分离式双矿柱体系模型，依靠散斑测量系统和声发射监测手段记录了各矿柱所承担的荷载以及矿柱的变形与声发射信息，进而分析应力转移规律及变形破坏特征；主要结论是：低强度矿柱先出现裂纹，承载能力缓慢下降，与此同时荷载向高强度矿柱转移，当高强度矿柱出现宏观滑移时，双矿柱试样组整体丧失承载能力；单个矿柱的承载能力、应力状态及外部荷载与能量环境均对双矿柱体系的整体稳定性有着显著的影响。ZHOU[190]等对双柱试件的破坏过程进行了试验和数值模拟研究，发现弹性模量较高或强度较低的试样会首先失去承载力，并认为该类型矿柱是矿柱体系中的薄弱环节。

对于“整体式双矿柱体系模型”，其主要特点是它考虑了矿柱与顶底板的相互作用关系，试验过程中除了可以获得矿柱的失稳破坏形式，同时还可以观察到矿柱对顶底板的作用结果，因此整体式双矿柱体系模型的设计方法更加符合现场实际情况。但是整体式双矿柱体系物理模型不能单独监测每个矿柱的应力-应变数据，试验获取的结果仅仅是双矿柱体系整体的应力-应变关系，因此无法获得单个矿柱的变形、承载和失稳特性。对于“分体式双矿柱体系模型”，其矿柱模型的制作更加简单，而且通过在2个并联矿柱下分别安装压力传感器和位移计，可以较容易地获得单个矿柱的应力-应变数据，随后对2组数据进行对比以获取2个矿柱间的协同作用特性。但是分离式双矿柱体系模型无法考虑矿柱对顶底板的破坏特性的影响以及矿柱与顶底板之间的协同作用机制。

为了揭示多矿柱系统在变形与失稳破坏过程中伴随的载荷传递和能量转移行为，笔者所在课题组开展了并联多矿柱失稳破坏行为的试验研究，试验方案如图7所示[191]。图7( a )为三矿柱-顶底板系统简化物理模型，在远场围岩体的载荷作用下，多矿柱和顶底板发生压缩变形，并最终发生破坏。图7( b )为三矿柱-顶底板系统简化物理模型的试验方法，即采用3个标准圆柱试样模拟多矿柱系统，通过不同数量的碟簧组定量化模拟顶底板的弹性变形和储能行为，试验机加载系统模拟远场围岩体的加载行为。在多矿柱-顶底板系统的整个变形破坏过程中，顶底板始终处于弹性阶段，并能够储存大量的弹性能，其回弹行为将对多矿柱的荷载传递和失稳破坏行为产生重要影响。

图7 三矿柱-顶底板系统试验示意Fig. 7 Schematic diagram of physical experiment of roof-treble-pillar-floor system

图8展示了W-Y-R试样( 白色、黄色和红色砂岩 )的依次失稳破坏试验结果，得出试样R，W和Y依次在828.02，898.52，942.10 s发生失稳破坏。由图8可知，试样的破坏过程可分为以下几个阶段：① 试样R首先破坏，荷载下降66.44 kN，碟簧组回弹并压缩试样W和Y，导致试样W和Y的荷载激增17.52 kN和10.77 kN。由图8( c )可知，试样R破坏引起碟簧组回弹0.18 mm和弹性能释放3.61 J；试样W和试样Y的弹性能由于碟簧组回弹的压缩作用，分别增加了1.75 J和0.66 J。② 随后试样W破坏，荷载下降104.26 kN，碟簧组回弹并引起试样Y的荷载激增24.93 kN。由图8( c )可知，试样W破坏引起碟簧组回弹0.68 mm和弹性能释放26.13 J；试样Y的弹性能由于碟簧组回弹的压缩作用增加了8.51 J。③ 最后，试样Y破坏，载荷下降84.61 kN，碟簧组回弹1.06 mm，弹性能量释放33.74 J。

图8 多矿柱试样依次失稳破坏Fig. 8 Experimental result of successive failure mode of multiple pillar system

通过以上研究发现，顶底板的弹性变形( 或柔性加载条件 )是多矿柱荷载传递的必要条件；当某一矿柱发生失稳破坏时，顶底板将发生回弹，并对剩余矿柱产生应力叠加作用( 即动静组合加载 )，动载荷将导致剩余矿柱载荷激增( 即载荷传递 )。因此，顶板的变形回弹是引起矿柱间载荷传递的物理本质；载荷传递的大小决定了剩余矿柱变形及破坏特征，当载荷传递超过剩余矿柱的承载极限时，将诱发多矿柱的连锁性失稳破坏行为。

研究重点与展望：多矿柱失稳破坏试验的材料消耗大、试验过程复杂、精度要求高，为此，在基于试验结果对数值模拟方法进行验证的基础上，可以采用数值模拟手段对物理试验进行补充和验证。利用数值模拟可以重复开展不同矿柱数量、尺寸及含结构面情况下的多矿柱失稳破坏行为研究，在降低研究投入的同时，拓展了研究内容。因此，在物理试验基础上，借由数值模拟手段拓展试验方案并对应大尺度的工程问题，是未来多矿柱承载及失稳破坏机制的重要研究思路之一。

2.3 多矿柱失稳破坏数值模拟

针对采空区群的失稳坍塌和多矿柱系统的失稳破坏灾害，国内外学者还开展了大量的数值模拟工作，以期揭示出采空区群与多矿柱系统的损伤演化与失稳破坏机理[192-198]。ZHOU[190]等对双矿柱试件的破坏过程进行了试验和数值模拟研究，再现了弹性模量较高或强度较低的试样会首先失去承载力的现象；WANG[179]等对多矿柱的破坏机制进行了数值模拟分析，揭示了矿柱的刚度和单轴抗压强度对多矿柱的失稳破坏过程的重要控制作用；KAISER和TANG[178]利用RFPA2D研究了顶底板回弹对单矿柱破坏模式的影响，发现具有柔性力学特性的围岩通过释放其储存的弹性能，导致了矿柱的失稳破坏，证实了柔性加载系统对多矿柱体系失稳破坏的影响，并揭示了双矿柱体系的损伤演化及失稳破坏机制；宋卫东[169]等借助FLAC3D数值模拟软件对石人沟铁矿采空区群所在区域的应力场、位移场进行了分析，发现群效应增加了采空区的危险等级；吴启红[199]等利用数值模拟和多级模糊评价相结合的方法，对多层采空区群的稳定性进行了评价；刘晓明[200]等运用Phase软件分析了某矿山矿房采场依次回采后矿房、矿柱内部应力和位移的分布特征；陈伟[192]利用3DMINE-MIDAS/GTS-FLAC3D多软件耦合技术建立了复杂采空区群三维数值计算模型，然后应用FLAC3D软件模拟分析了采空区群在静力和爆破荷载组合作用下的应力、位移、塑性区和地表沉降分布规律；吴亚斌[193]基于三维激光探测系统的扫描结果和SURPAC三维建模软件，建立了采空区群三维几何模型，并导入FLAC3D数值模拟软件进行采空区群的稳定性分析；刘超[195]等建立了采空区群三维数值模型，利用MIDAS数值模拟软件对采空区群的大规模失稳现象进行模拟分析；付建新[201]等建立了采空区群FLAC3D数值计算模型，对采空区群的“群效应”进行了模拟研究，并发现“群效应”加剧了开采扰动对采空区的影响；姜立春[202-203]等利用RFPA数值模拟软件，建立纵向和横向采空区群动态失稳的等效数值模型，发现多列纵向采空区群比单列纵向采空区群的顶板更易发生破坏；多层水平采空区群岩体结构具有较好的稳定性，单层水平采空区群的间柱失稳过程较分散，而多层水平采空区群的间柱失稳过程则较集中。

DEHGHAN[70]等通过数值模拟的方法研究了一个具体的“多米诺”失稳破坏案例，用数值模拟方法与经验公式法研究了一个矿柱发生破坏导致其他矿柱逐渐坍塌，直到4 000 m2的矿井在几分钟内坍塌的载荷传递与破坏过程；通过比较发现，不合理的矿柱宽高比、不完善的支护系统、不合理的回采方案等因素是造成多矿柱连锁性失稳破坏的原因，并基于此提出预防“多米诺”破坏的方案。WANG[179]等利用RFPA数值模拟软件模拟了双矿柱和三矿柱试样的破坏模式，研究了矿柱的刚度和单轴抗压强度对矿柱失稳破坏先后顺序的影响；ZHANG[145]等研究了多矿柱损伤演化过程中的载荷传递机制，发现当传递载荷超过相邻矿柱强度时，会引起多矿柱的连锁性失稳破坏行为，即矿柱失稳的“多米诺”效应；LI[157]等基于房柱法开采的具体矿山案例，建立了矿柱-顶底板系统模型，从能量角度分析了模型失稳与系统刚度的关系，并利用UDEC模拟了“多米诺”效应的发生条件，并认为矿柱宽度越大，“多米诺”失稳破坏行为发生的可能性越低；陈柘儒[204]以某矿山的矿房式开采方案为例，利用ABAQUS数值模拟软件模拟研究了多矿柱支撑系统在受动载扰动时的响应规律，以及多矿柱系统的连锁性失稳破坏过程，探究了矿柱不同宽高比情况下的动态扰动结果，模拟了多矿柱系统发生连锁性失稳时，矿柱间的能量、应力转移行为及其导致整个系统发生失稳坍塌的现象。表1列举了具有代表性的多矿柱失稳破坏模式研究成果。

表1 多矿柱系统失稳破坏模式汇总Table 1 Unstable failure mode of multi-pillar system

续 表

此外，笔者利用RFPA数值模拟软件开展了与图8对应的多矿柱连锁性失稳破坏行为的数值模拟研究，表2展示了3种矿柱所采用的宏观力学参数和细观数值模拟参数，图9展示了柔性加载条件下WY-R试样的数值模拟结果。试样R，W和Y分别在821，910和922步发生失稳破坏。可知，试样的破坏过程可分为几个阶段：① 试样R首先破坏，荷载下降68.54 kN，引起试样W和Y的荷载激增10.79 kN和8.60 kN。试样R破坏引起碟簧组回弹0.418 mm和弹性能释放14.41 J；试样W和Y在碟簧组回弹的压缩作用下，弹性能分别增加4.03 J和2.68 J。② 试样W随后破坏，荷载下降了113.57 kN，引起试样Y荷载激增4.77 kN。试样W的破坏引起碟簧组回弹0.420 mm和弹性能释放14.55 J；试样Y由于碟簧组回弹的压缩作用，弹性能增加5.42 J。③ 试样Y最终破坏，载荷下降81.81 kN；碟簧组回弹0.584 mm至恢复原状，弹性能释放28.14 J。图9( c )为W-Y-R数值模型在柔性加载条件下的失稳破坏模式，数值模拟得到的载荷与能量传递数值与试验结果在量级和趋势上有良好的一致性，试样破坏顺序也与试验结果一致。

图9 多矿柱依次失稳破坏数值模拟结果Fig. 9 Numerical results of successive failure mode

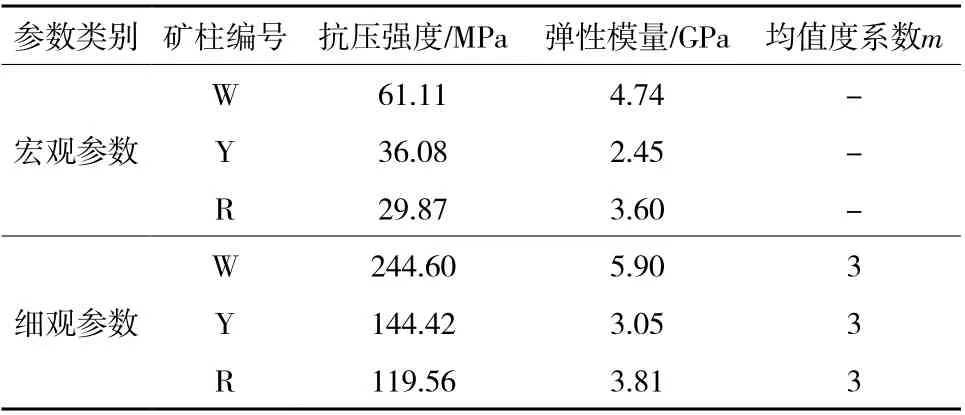
表2 基本力学参数Table 2 Basic mechanical parameters

研究重点与展望：通过理论分析和物理试验方法研究多矿柱的失稳破坏过程及载荷传递机制是认识该问题的重要手段。然而，由于理论模型过于简化且考虑的因素有限，难以反映工程实际；物理试验难度大、精度要求高，需要构建多矿柱的关联承载系统并严格控制加载条件，以使其符合工程实际。相比之下，数值模拟可以建立复杂的工程模型，优势明显。基于工程案例的详尽考察资料，建立大规模采空区群数值分析模型，可以充分发挥数值模拟的优势，对多矿柱-顶底板系统的整体协同变形与失稳破坏行为进行预测分析，并基于此提出更加科学合理的处理方案，这是未来研究多矿柱承载及失稳破坏机制的重要思路之一。

3 工程案例分析

基于工程案例资料，建立矿井大规模采空区群数值分析模型，可以充分发挥数值模拟的优势，对多矿柱的整体协同变形与失稳破坏行为进行预测分析，并基于此提出更加科学合理的采空区处理方案。作为多矿柱和采空区群处理的典型案例，红岭铅锌矿的采空区群处理和残矿回收具有代表性。经过多年开采，该矿遗留了大量的采空区，同一阶段水平采空区之间相互贯通，不同回采阶段采空区相互影响，共同构成了复杂的多矿柱[5,205-207]采空区群。胡高建[205]等利用COMSOL数值模拟软件研究了红岭铅锌矿多中段回采过程中围岩体的损伤破坏机理；赵永[206]等基于VR技术建立了该矿的矿山虚拟现实系统，再现了复杂的多矿柱空间分布，并利用FLAC3D软件对采空区稳定性进行数值模拟，并与Mathews图表法所评价的采空区群稳定概率进行对比分析[207]；王薪荣[1]建立了红岭铅锌矿大规模采空区群的三维地质模型，利用FLAC3D软件模拟分析了采空区群的应力场、位移场，并结合模拟结果提出了最佳多矿柱回收方案。

笔者所在课题组以阿尔哈达铅锌矿848 m中段4个矿柱( P1-2,P2-3,P3-4和P4-5)和5个采空区( 1号，2号，3号，4号和5号 )所组成的多矿柱系统为研究对象( 图10 )，利用RFPA2D岩石破裂过程分析软件模拟多矿柱系统的动态失稳演化过程，并基于刚度理论分析其失稳破坏特征及载荷传递行为。

图10 多矿柱( 采空区群 )三维模型Fig. 10 3D model of multi-pillar system ( or goaf group )

( 1 ) 矿柱破坏过程稳定性分析

比较矿柱P1-2，P2-3，P3-4和P4-5的峰后刚度(k1-2＝46.38 GN/m，k2-3＝47.73 GN/m，k3-4＝44.08 GN/m，k4-5＝47.95 GN/m )和所在地层的局部刚度(K1-2＝37.39 GN/m，K2-3＝32.69 GN/m，K3-4＝31.85 GN/m，K4-5＝38.20 GN/m )可知，所有矿柱的刚度比值( 即K1-2/k1-2，K2-3/k2-3，K3-4/k3-4和K4-5/k4-5)均小于1。根据SALAMON刚度准则[39]，当载荷超过各矿柱的承载极限时，各矿柱将发生失稳破坏。

( 2 ) 多矿柱载荷传递、变形突跳及弹性能释放

由图11( a )可知，模型中部双矿柱( P2-3和P3-4)首先发生连锁性失稳破坏，引起模型两侧双矿柱( P1-2和P4-5)的载荷激增( 即载荷传递 )，增量分别为714.81，480.03 MN。载荷传递没有超过双矿柱( P1-2和P4-5)的承载极限，因此没有引起连锁破坏。矿柱P1-2，P2-3，P3-4和P4-5发生失稳破坏时的变形突跳( 或其所在顶底板的回弹 )分别为105.26，63.91，106.19，69.36 mm；各矿柱所在顶底板的释放弹性能W1-2，W2-3，W3-4和W4-5分 别 为102.87，133.84，137.59，100.26 MJ。

图11 多矿柱载荷传递及变形突跳结果Fig. 11 Load transfer and sudden jump displacement of multi-pillar

( 3 ) 多矿柱失稳破坏模式

如图12所示，通过对数值模拟结果进行分析，并绘制多矿柱系统的载荷-位移曲线可知，阿尔哈达铅锌矿848 m中段多矿柱系统共经历了2次双矿柱连锁性失稳破坏，分别为双矿柱P2-3和P3-4连锁性失稳破坏a—b，以及双矿柱P1-2和P4-5连锁性失稳破坏c—d。第1次连锁性失稳破坏导致顶底板回弹86.66 mm，释放弹性能254 MJ；第2次连锁性失稳破坏导致顶底板回弹119.82 mm，释放弹性能486 MJ。综上所述，阿尔哈达铅锌矿848 m中段多矿柱系统的失稳破坏模式为“2+2”形式的复合型失稳破坏模式。

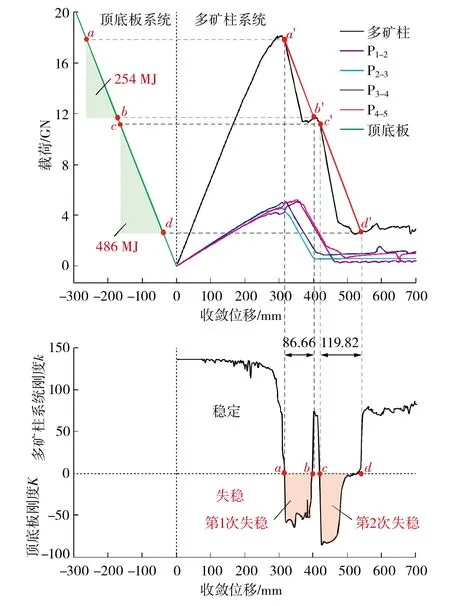
图12 多矿柱系统载荷-位移曲线Fig. 12 Load-displacement curves of multi-pillar system

( 4 ) 多矿柱连锁性失稳破坏防控措施及建议

针对阿尔哈达铅锌矿多矿柱系统的复合型失稳破坏模式，可以采用锚杆加固法、卸压法和充填法等进行防控。① 锚杆加固法是指通过给矿柱加装锚杆来提高多矿柱系统的稳定性和承载能力；② 卸压法是指围岩卸压或矿柱卸压，对于矿柱和围岩体组成的二维系统，通过释放其中任意一方的应力来起到改善岩石工程应力环境的作用；③ 充填法是指利用充填体充填采空区，约束多矿柱系统的横向变形，进而提高多矿柱系统的承载能力。除此之外，在矿山设计阶段应尽量保证：① 为提高矿柱强度，采出率不超过60%；② 矿柱的宽高比W/H>1，保证矿柱的残余承载能力；③ 留设宽高比W/H>10的坚固隔离矿柱，起到隔断矿柱失稳传播的作用。

4 结 语

对单矿柱和多矿柱系统的稳定性，以及多矿柱系统失稳破坏的影响因素、载荷传递机制等方面进行了总结和论述。文献综述表明，对于单矿柱的承载与失稳破坏行为的研究，当前已经有很多经典的理论模型及分析方法；然而，对于多矿柱系统的研究手段却较为单一，特别是对于载荷传递的理论及失稳判据的研究相对较少，尚缺乏可靠的力学模型和分析方法，同时也缺少相应的试验和数值模拟研究。根据已有研究成果可知，影响多矿柱系统稳定性的因素较多，且各因素之间存在相互作用，他们导致了多矿柱系统复杂的载荷传递与失稳破坏行为。因此，建立科学合理的多矿柱力学模型，并基于该模型提出有效的失稳判据和载荷传递理论分析方法，同时开展多矿柱失稳物理及数值模拟试验研究加以验证，是现阶段矿柱失稳破坏方面亟待解决的关键性问题。因此在未来研究发展过程中，数值模拟将起到越来越重要的辅助研究作用，需要深入开展多矿柱的承载、失稳破坏及载荷传递过程的数值模拟研究工作。

笔者在多矿柱关联失稳破坏方面的研究成果有助于理解大规模采空区群失稳破坏的内在关联机制，并据此提出科学有效的防控措施，保证矿产资源的安全高效开采。即便如此，鉴于实际工程中的多矿柱-顶底板系统及矿柱间的相互作用行为更为复杂，且应力状态及损伤程度难以完全探测清楚，以往认为上覆岩层的载荷重分布从而引起多矿柱连锁失稳破坏行为的诱因是过于浅显的，当前的研究尚不足以揭示多矿柱载荷传递的物理本质，该问题仍有待结合工程实践开展深入研究。此外，在实际工程中应加强对多矿柱-顶底板系统的监测和分析，探索载荷传递过程中所伴随的应力、变形突变及微震事件激增等现象，进而预防多矿柱系统大规模失稳破坏事故的发生。

参考文献( References )：

[1] 王薪荣. 红岭铅锌矿采空区稳定性分析[D]. 沈阳：东北大学，2014.WANG Xinrong. Stability analysis of mined-out area in Hongling Lead-Zinc Mine[D]. Shenyang：Northeastern University，2014.

[2] 姜立春，罗恩民，沈彬彬. 多自由度模型法的立体采空区群爆破动力响应研究[J]. 岩土力学，2019，40( 6 )：1-10.JIANG Lichun，LUO Enmin，SHEN Binbin. A dynamic response of blasting to stereoscopic goaf group based on the multi-degree of freedom model method[J]. Rock and Soil Mechanics，2019，40( 6 )：1-10.

[3] 王启明. 非煤矿山安全生产形势、问题及对策[J]. 金属矿山，2005，34( 10 )：1-6.WANG Qiming. Situation of safety production in non-coal mines and its problems and countermeasures[J]. Metal Mine，2005，34( 10 )：1-6.

[4] 马海涛，刘宁武，王云海，等. 金属矿山采空区灾害防治技术研究综述[J]. 中国安全生产科学技术，2014，10( 10 )：75-80.MA Haitao，LIU Ningwu，WANG Yunhai，et al. Review on research status of controlling techniques for goaf disaster in metal mine[J].Journal of Safety Science and Technology，2014，10( 10 )：75-80.

[5] 王启明，鲍爱华. 我国非煤矿山安全生产现状与技术发展[J]. 采矿技术，2005，5( 2 )：11-13.WANG Qiming ，BAO Aihua. Present situation and technical development of safety production in non coal mines in China[J].Mining Technology，2005，5( 2 )：11-13.

[6] 彭欣. 复杂采空区稳定性及近区开采安全性研究[D]. 长沙：中南大学，2008.PENG Xin. Study on stability of complex cavity and safety in nearcavity excavation[D]. Changsha：Central South University，2008.

[7] 潘一山. 冲击地压发生和破坏过程研究[D]. 北京：清华大学，1999.PAN Yishan. Study on rockburst initiation and failure propagation[D].Beijing：Tsinghua University，1999.

[8] PENG S S. Ground control failures-a pictorial view of case studies[M].Morgantown，WV，U. S. A：West Virginia University Press，2007.

[9] SZWEDZICKI T. Geotechnical precursors to large-scale ground collapse in mines[J]. International Journal of Rock Mechanics and Mining Sciences，2001，38( 7 )：957-965.

[10] WANG J A，SHANG X C，MA H T. Investigation of catastrophic ground collapse in Xingtai gypsum mines in China[J]. International Journal of Rock Mechanics and Mining Sciences，2008，45( 8 )：1480-1499.

[11] ESTERHUIZEN G S，DOLINAR D R，ELLENBERGER J R，et al.Pillar and roof span design guidelines for underground stone mines[A].Pittsburgh，USA：National Institute for Occupational Safety and Health[C]. 2011：1-64.

[12] 颜荣贵. 地基开采沉陷及其地表建筑[M]. 北京：冶金工业出版社，1995：262-268.YAN Ronggui. Foundation mining subsidence and its surface construction[M]. Beijing：Metallurgical Industry Press，1995：262-268.

[13] 吴启红. 矿山复杂多层采空区稳定性综合分析及安全治理研究[D]. 长沙：中南大学，2010.WU Qihong. Analyzing stability synthetically and researching treatment methods on the complicated multi-layer mine-out areas[D].Changsha：Central South University，2010.

[14] 郭治安. 协同学入门[M]. 成都：四川人民出版社，1988：1-368.GUO Zhian. Introduction to synergetics[M]. Chengdu：Sichuan People's Publishing House，1988：1-368.

[15] HUSTRULID W A. A review of coal pillar strength formulas[J]. Rock Mechanics and Rock Engineering，1976，8( 2 )：115-145.

[16] GADDY F L. A study of the ultimate strength of coal as related to the absolute size of cubical specimens tested[J]. West Virginia Polytechnic Bulletin，1956，112：1-27.

[17] LUNDER P，PAKALNIS R. Determination of the strength of hard-rock mine pillars[J]. CIM Bulletin，1997，9：51-55.

[18] ESTERHUIZEN G S，DOLINAR D R，ELLENBERGER J L. Pillar strength in underground stone mines in the United States[J].International Journal of Rock Mechanics & Mining Sciences，2011，48( 1 )：42-50.

[19] FANG Z，HARRISON P J. Numerical analysis of progressive fracture and associated behaviour of mine pillars by use of a local degradation model[J]. Mining Technology，2002，111( 1 )：59-72.

[20] JAISWAL A，SHRIVASTVA B K. Numerical simulation of coal pillar strength[J]. International Journal of Rock Mechanics and Mining Sciences，2009，46( 4 )：779-788.

[21] MORTAZAVI A，HASSANI F P，SHABANI M. A numerical investigation of rock pillar failure mechanism in underground openings[J]. Computers & Geotechnics，2009，36( 5 )：691-697.

[22] POULSEN B A. Coal pillar load calculation by pressure arch theory and near field extraction ratio[J]. International Journal of Rock Mechanics and Mining Sciences，2010，47( 7 )：1158-1165.

[23] 丘帆，马海涛，欧阳明，等. 基于Voronoi图和时间效应的矿柱失稳预测[J]. 中国安全生产科学技术，2014，35( 2 )：38-43.QIU Fan，MA Haitao，OUYANG Ming，et al. Prediction of pillar instability based on Voronoi chart and time effect[J]. Journal of Safety Science and Technology，2014，35( 2 )：38-43.

[24] JAISWAL A，SHARMA S K，SHRIVASTVA B K. Numerical modeling study of asymmetry in the induced stresses over coal mine pillars with advancement of the goaf line[J]. International Journal of Rock Mechanics and Mining Sciences，2004，41( 5 )：859-864.

[25] GHASEMI E，SHAHRIAR K. A new coal pillars design method in order to enhance safety of the retreat mining in room and pillar mines[J]. Safety Science，2012，50( 3 )：579-585.

[26] 刘陶安，刘芹. 矿柱设计中的岩石力学问题[J]. 世界采矿快报，1993( 33 )：18-20.LIU Taoan，LIU Qin. Rock mechanics in pillar design[J]. W orld Mining Express，1993( 33 )：18-20.

[27] 罗斌玉，叶义成，李玉飞，等. Mohr-Coulomb准则下倾斜矿柱稳定性的安全系数法[J]. 煤炭学报，2018，43( 9 )：46-53.LUO Binyu，YE Yicheng，LI Yufei，et al. Safety factor method for stability of inclined pillars under Mohr-Coulomb criterion[J]. Journal of China Coal Society，2018，43( 9 )：46-53.

[28] 刘沐宇，徐长佑. 地下采空区矿柱稳定性分析[J]. 矿冶工程，2000，20( 1 )：19-22.LIU Muyu，XU Changyou. Stability analysis of pillars in minedout area[J]. Mining and Metallurgical Engineering，2000，20( 1 )：19-22.

[29] 杨宇江，李元辉. 基于加卸载响应比理论的矿柱动力稳定性分析[J]. 岩土力学，2013，34( S1 )：324-330.YANG Yujiang，LI Yuanhui. Dynamic stability analysis of pillar based on loading-unloading response ratio theory[J]. Rock and Soil Mechanics，2013，34( S1 )：324-330.

[30] 李江腾. 硬岩矿柱失稳及时间相依性研究[D]. 长沙：中南大学，2005.LI Jiangteng. Study on instability and time dependence of pillar in hard rock mass[D]. Changsha：Central South University，2005.

[31] 罗斌玉，叶义成，曹中，等. 基于Mohr-Coulomb准则的缓倾斜层状矿床矿柱强度估算及倾角效应[J]. 岩土力学，2019，40( 5 )：1940-1946.LUO Binyu，YE Yicheng，CAO Zhong，et al. Estimation of pillar strength and effect of inclination under gently inclined layered deposits based on Mohr-Coulomb criterion[J]. Rock and Soil Mechanics，2019，40( 5 )：1940-1946.

[32] 彭斌，陈才贤，杨军伟. 石膏矿矿柱稳定性分析及试验研究[J].采矿技术，2011，11( 2 )：18-21.PENG Bin，CHEN Caixian，YANG Junwei. Stability analysis and experimental study of gypsum ore pillar[J]. Mining Technology，2011，11( 2 )：18-21.

[33] MA H，WANG J，WANG Y. Study on mechanics and domino effect of large-scale goaf cave-in[J]. Safety Science，2012，50( 4 )：689-694.

[34] 王金安，李大钟，马海涛. 采空区矿柱-顶板体系流变力学模型研究[J]. 岩石力学与工程学报，2010，29( 3 )：577-582.WANG Jin'an，LI Dazhong，MA Haitao. Study of rheological mechanical model of pillar-roof system in mined-out area[J]. Chinese Journal of Rock Mechanics and Engineering，2010，29( 3 )：577-582.

[35] COOK N G W. The failure of rock[J]. International Journal of Rock Mechanics & Mining Sciences & Geomechanics Abstracts，1965，2( 4 )：389-403.

[36] CHEN Z H，TANG C A，HUANG R Q. A double rock sample model for rockbursts[J]. International Journal of Rock Mechanics and Mining Sciences，1997，34( 6 )：991-1000.

[37] 尤明庆. 岩石的力学性质[M]. 北京：地质出版社，2007：1-316.YOU Mingqing. Mechanical properties of rock[M]. Beijing：Geological Publishing House，2007：1-316.

[38] 尤明庆. 岩样单轴压缩的失稳破坏和试验机加载性能[J]. 岩土力学，1998，19( 3 )：43-49.YOU Mingqing. Instable failure of rock specimen in uniaxial compression and the loading behavior of testing machine[J]. Rock and Soil Mechanics，1998，19( 3 )：43-49.

[39] SALAMON M D G. Stability，instability and design of pillar workings[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts，1970，7( 6 )：613-631.

[40] ZIPF R K，MARK C. Design methods to control violent pillar failures in room-and-pillar mines[J]. Mining Technology IMM Transactions Section A，1997，106：A124-A132.

[41] YAVUZ H. Yielding pillar concept and its design[A]. Proceedings of 17th International Mining Congress and Exhibition[C]. Turkey，2001：397-404.

[42] THOM R. Stabilité structurelle et morphogénèse[J]. W. A.Benjamin，1972，36( 5/6 )：611-613.

[43] THOMPSON J M T，LEIPHOLZ H H E. Instabilities and catastrophes in science and engineering[J]. Journal of Applied Mechanics，1982，49( 4 )：932.

[44] ZEEMAN C. The classification of elementary catastrophes of codimension≤5[M]. Berlin：Springer Berlin Heidelberg，1976：263-327.

[45] ZEEMAN E C. Bifurcation，catastrophe，and turbulence[M]. New York：Springer，1982：109-153.

[46] POSTON T，STEWART I，PLAUT R H. Catastrophe theory and its applications[J]. Bulletin of Mathematical Biology，1979，41( 4 )：615-616.

[47] 唐春安. 岩石破裂过程中的灾变[M]. 北京：煤炭工业出版社，1993：1-126.TANG Chun'an. Catastrophe in rock unstable failure[M]. Beijing：China Coal Industry Publishing House，1993：1-126.

[48] 郭文兵，邓喀中，邹友峰. 走向条带煤柱破坏失稳的尖点突变模型[J]. 岩石力学与工程学报，2004，23( 12 )：1996-2000.GUO Wenbing，DENG Kazhong，ZOU Youfeng. CUSP catastrophic model of instability of strip coal pillar along strike[J]. Chinese Journal of Rock Mechanics and Engineering，2004，23( 12 )：1996-2000.

[49] 徐曾和，徐小荷. 坚硬顶板下煤柱岩爆的尖点突变理论分析[J].煤炭学报，1995，20( 5 )：485-491.XU Zenghe，XU Xiaohe. Theoretical analysis of a cusp catastrophe bump of coal pillar under hard rocks[J]. Journal of China Coal Society，1995，20( 5 )：485-491.

[50] 徐曾和，徐小荷. 柱式开采岩爆发生条件与时间效应的尖点突变[J]. 中国有色金属学报，1997，7( 2 )：17-23.XU Zenghe，XU Xiaohe. Cusp catastrophe of occurrence conditions and hysteresis of rockbursts in pillar workings[J]. Journal of Nonferrous Metals，1997，7( 2 )：17-23.

[51] LI J，CAO P. Cusp catastrophe model of instability of pillar in asymmetric mining[J]. Applied Mathematics and Mechanics，2005，26( 8 )：1100-1106.

[52] WANG S Y，AU S K，LAM K C，et al. A numerical study of pillar failure based on a cusp-type catastrophe model[J]. Key Engineering Materials，2005，297-300：2628-2635.

[53] QIN S，JIAO J J，TANG C A，et al. Instability leading to coal bumps and nonlinear evolutionary mechanisms for a coal-pillar-and-roof system[J]. International Journal of Solids and Structures，2006，43( 25-26 )：7407-7423.

[54] 李江腾，曹平. 硬岩矿柱纵向劈裂失稳突变理论分析[J]. 中南大学学报( 自然科学版 )，2006，37( 2 )：371-375.LI Jiangteng，CAO Ping. Analysis of pillar stability in hard rock mass by longitudinal splitting based on catastrophe theory[J]. Journal of Central South University( Science and Technology )，2006，37( 2 )：371-375.

[55] 王连国，缪协兴. 基于尖点突变模型的矿柱失稳机理研究[J]. 采矿与安全工程学报，2006，23( 2 )：137-140.WANG Lianguo，MIAO Xiexing. Study of mechanism of destabilization of the mine pillar based on a cusp catastrophic model[J]. Journal of Mining & Safey Engineering，2006，23( 2 )：137-140.

[56] 谷惠棠，胡慧明. 基于突变理论的矿柱失稳破坏研究[J]. 金属矿山，2011，40( 8 )：15-18.GU Huitang，HU Huiming. Study on instability and failure of the mine pillar based on catastrophe theory[J]. Metal Mine，2011，40( 8 )：15-18.

[57] 江文武，徐国元，马长年. 基于尖点突变理论的矿房间矿柱的稳定性分析[J]. 金属矿山，2007，36( 9 )：39-41.JIANG Wenwu，XU Guoyuan，MA Changnian. Stability analysis of intermittent pillar between stope rooms based on cusp catastrophe theory[J]. Metal Mine，2007，36( 9 )：39-41.

[58] 潘岳，王志强，李爱武. 岩石失稳破裂的综合刚度和综合能量准则[J]. 岩土力学，2009，30( 12 )：3671-3676.PAN Yue，WANG Zhiqiang，LI Aiwu. Comprehensive rigidity and comprehensive energy criterion of the rock burst[J]. Rock and Soil Mechanics，2009，30( 12 )：3671-3676.

[59] 张黎明，王在泉，张晓娟，等. 岩体动力失稳的折迭突变模型[J].岩土工程学报，2009，31( 4 )：552-557.ZHANG Liming，WANG Zaiquan，ZHANG Xiaojuan，et al. Fold catastrophe model of rock dynamic destabilization[J]. Chinese Journal of Geotechnical Engineering，2009，31( 4 )：552-557.

[60] 王志强，张立新，潘岳. 岩体动力失稳及能量释放特征分析[J].金属矿山，2011，40( 8 )：33-36.WANG Zhiqiang，ZHANG Lixin，PAN Yue. Analysis on rock dynamic destabilization and energy releasing characteristics[J]. Metal Mine，2011，40( 8 )：33-36.

[61] 付成华，陈胜宏. 基于突变理论的地下工程洞室围岩失稳判据研究[J]. 岩土力学，2008，29( 1 )：167-172.FU Chenghua，CHEN Shenghong. Study on instability criteria of surrounding rock of underground engineering cavern based on catastrophe theory[J]. Rock and Soil Mechanics，2008，29( 1 )：167-172.

[62] 张钦礼，曹小刚，王艳利，等. 基于尖点突变模型的采场顶板-矿柱稳定性分析[J]. 中国安全科学学报，2011，21( 10 )：52-57.ZHANG Qinli，CAO Xiaogang，WANG Yanli，et al. Stability analysis of stope roof-pillar based on cusp catastrophe model[J]. China Safety Science Journal，2011，21( 10 )：52-57.

[63] 陈庆发，古德生，周科平，等. 对称协同开采人工矿柱失稳的突变理论分析[J]. 中南大学学报( 自然科学版 )，2012，43( 6 )：2338-2342.CHEN Qingfa，GU Desheng，ZHOU Keping，et al. Analysis of catastrophe theory for artificial pillar instability in symmetric synergistic mining[J]. Journal of Central South University( Science and Technology )，2012，43( 6 )：2338-2342.

[64] LIU C，TAN Z，DENG K，et al. Synergistic instability of coal pillar and roof system and filling method based on plate model[J]. International Journal of Mining Science & Technology，2013，23( 1 )：145-149.

[65] XIA K，CHEN C，ZHOU Y，et al. Catastrophe instability mechanism of the pillar-roof system in gypsum mines due to the influence of relative humidity[J]. International Journal of Geomechanics，2019，19：1-16.

[66] 夏开宗，陈从新，刘秀敏，等. 基于突变理论的石膏矿矿柱-护顶层支撑体系的破坏分析[J]. 岩石力学与工程学报，2016，35(S2 )：3837-3845.XIA Kaizong，CHEN Congxin，LIU Xiumin，et al. Study of the failure of pillar-roof system in gypsum mines based on catastrophe theory[J].Chinese Journal of Rock Mechanics and Engineering，2016，35(S2 )：3837-3845.

[67] 高明仕，窦林名，张农，等. 煤( 矿 )柱失稳冲击破坏的突变模型及其应用[J]. 中国矿业大学学报，2005，34( 4 )：433-437.GAO Mingshi，DOU Linming，ZHANG Nong，et al. Cusp catastrophic model for instability of coal pillar burst damage and analysis of its application[J]. Journal of China University of Mining & Technology，2005，34( 4 )：433-437.

[68] 贺广零，黎都春，翟志文，等. 采空区煤柱-顶板系统失稳的力学分析[J]. 煤炭学报，2007，32( 9 )：897-901.HE Guangling，LI Duchun，ZHAI Zhiwen，et al. Analysis of instability of coal pillar and stiff roof system[J]. Journal of China Coal Society，2007，32( 9 )：897-901.

[69] LI X，LI D，LIU Z，et al. Determination of the minimum thickness of crown pillar for safe exploitation of a subsea gold mine based on numerical modelling[J]. International Journal of Rock Mechanics &Mining Sciences，2013，57：42-56.

[70] DEHGHAN S，SHAHRIAR K，MAAREFVAND P，et al. 3-D numerical modelling of Domino failure of hard rock pillars in Fetr6 Chromite Mine，Iran，and comparison with empirical methods[J].Journal of Central South University，2013，20( 2 )：541-549.

[71] AKSOY C O，ONARGAN T. Sizing room and pillar by numerical modeling for underground marble quarries in Turkey[J]. Journal of Mining Science，2006，42( 5 )：483-489.

[72] ELMO D，STEAD D. An integrated numerical modelling-discrete fracture network approach applied to the characterisation of rock mass strength of naturally fractured pillars[J]. Rock Mechanics and Rock Engineering，2010，43( 1 )：3-19.

[73] 赵奎，蔡美峰，饶运章，等. 某金矿残留矿柱回采的稳定性研究[J].有色金属，2003，55( 2 )：82-84.ZHAO Kui，CAI Meifeng，RAO Yunzhang，et al. Stability of residual pillars recovery in a gold mine[J]. Nonferrous Metals，2003，55( 2 )：82-84.

[74] 郭建军. 夏甸金矿矿柱及围岩稳定性分析与应用[D]. 青岛：山东科技大学，2005.GUO Jianjun. Study and application on the stability of the mine pillars and surrounding rocks in Xiadian Gold Mine[D]. Qingdao：Shandong University of Science and Technology，2005.

[75] 赵兴东. 谦比希矿深部开采隔离矿柱稳定性分析[J]. 岩石力学与工程学报，2010，29( S1 )：2616-2622.ZHAO Xingdong. Stability analysis of insulating pillar of excavation of Chambishi Copper Mine in depth[J]. Chinese Journal of Rock Mechanics and Engineering，2010，29( S1 )：2616-2622.

[76] RAFIEI Renani H，MARTIN C D. Modeling the progressive failure of hard rock pillars[J]. Tunnelling and Underground Space Technology，2018，74：71-81.

[77] IANNACCHIONE A T. Numerical simulation of coal pillar loading with the aid of a strain-softening finite difference model[A]. 30th U. S.Symp. on Rock Mech.[C]. Morgantown，WV，1989：775-782.

[78] WHYATT J K，BOARD M P. Numerical exploration of shear-fracturerelated rock bursts using a strain-softening constitutive law[R].Washington，D C，USA：US Department of the Interior，Bureau of Mines，1991.

[79] MARTIN C D，MAYBEE W G. The strength of hard-rock pillars[J].International Journal of Rock Mechanics and Mining Sciences，2000，37( 8 )：1239-1246.

[80] DUNCAN Fama M E，TRUEMAN R，CRAIG M S. Two- and threedimensional elasto-plastic analysis for coal pillar design and its application to highwall mining[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts，1995，32( 3 )：215-225.

[81] ADHIKARY D P，SHEN B，FAMA M E D. A study of highwall mining panel stability[J]. International Journal of Rock Mechanics and Mining Sciences，2002，39( 5 )：643-659.

[82] 李夕兵，李地元，郭雷，等. 动力扰动下深部高应力矿柱力学响应研究[J]. 岩石力学与工程学报，2007，26( 5 )：922-928.LI Xibing，LI Diyuan，GUO Lei，et al. Study on mechanical response of highly-stressed pillars in deep mining under dynamic disturbance[J].Chinese Journal of Rock Mechanics and Engineering，2007，26( 5 )：922-928.

[83] 王在泉，李华峰. 矿柱抗剪安全系数的数值计算方法及分析[J].采矿与安全工程学报，2010，27( 2 )：277-280.WANG Zaiquan，LI Huafeng. Numerical calculation method for shear safty coefficient of mine pillar[J]. Journal of Mining and Safety Engineering，2010，27( 2 )：277-280.

[84] 刘学增，翟德元. 矿柱可靠度设计[J]. 岩石力学与工程学报，2000，19( 1 )：85-88.LIU Xuezeng，ZHAI Deyuan. The reliability design of pillar[J].Chinese Journal of Rock Mechanics and Engineering，2000，19( 1 )：85-88.

[85] 周子龙，王亦凡，柯昌涛. “多米诺骨牌”破坏现象下的矿柱群系统可靠度评价[J]. 黄金科学技术，2018，26( 6 )：729-735.ZHOU Zilong，WANG Yifan，KE Changtao. Reliability evaluation of pillars system based on domino failure effect[J]. Gold Science and Technology，2018，26( 6 )：729-735.

[86] NAJAFI M，JALALI S E，BAFGHI A R Y，et al. Prediction of the confidence interval for stability analysis of chain pillars in coal mines[J]. Safety Science，2011，49( 5 )：651-657.

[87] GRIFFITHS D V，FENTON G A，LEMONS C B. Probabilistic analysis of underground pillar stability[J]. International Journal for Numerical and Analytical Methods in Geomechanics，2002，26( 8 )：775-791.

[88] WATTIMENA R K. Predicting the stability of hard rock pillars using multinomial logistic regression[J]. International Journal of Rock Mechanics and Mining Sciences，2014，71：33-40.

[89] WATTIMENA R K，KRAMADIBRATA S，SIDI I D，et al. Developing coal pillar stability chart using logistic regression[J]. International Journal of Rock Mechanics and Mining Sciences，2013，58：55-60.

[90] 刘沐宇，夏元友，徐长佑. 矿柱结构的应力测量及稳定性分析[J].金属矿山，1999，28( 4 )：5-7.LIU Muyu，XIA Yuanyou，XU Changyou. The stress measurement and the stability analysis of pillar structure[J]. Metal Mine，1999，28( 4 )：5-7.

[91] 郝先虎. 基于Fisher判别分析法的矿柱稳定性研究[J]. 煤炭技术，2014，33( 3 )：11-14.HAO Xianhu. Pillar stability study of mine construction based on Fisher discriminant analysis[J]. Coal Technology，2014，33( 3 )：11-14.

[92] SAIN Stephan R. The nature of statistical learning theory[J].Technometrics，1997，38( 4 )：409.

[93] ZHOU J，LI X B，SHI X Z，et al. Predicting pillar stability for underground mine using Fisher discriminant analysis and SVM methods[J]. Trans. Nonferrous Met. Soc. China，2011，21：2734-2743.

[94] 张睿，刘涛. AHP-Fuzzy法的缓倾斜薄矿体矿柱结构参数优化[J].世界有色金属，2016( 8 )：100-102.ZHANG Rui，LIU Tao. The pillar structural parameter optimization of inclined thin orebody based on AHP-fuzzy method[J]. World Nonferrous Metals，2016( 8 )：100-102.

[95] TAWADROUS A S，KATSABANIS P D. Prediction of surface crown pillar stability using artificial neural networks[J]. International Journal for Numerical & Analytical Methods in Geomechanics，2007，31( 7 )：917-931.

[96] IDRIS M A，SAIANG D，NORDLUND E. Stochastic assessment of pillar stability at Laisvall Mine using Artificial Neural Network[J].Tunnelling and Underground Space Technology，2015，49：307-319.

[97] ULUSAY R. The ISRM suggested methods for rock characterization，testing and monitoring：2007-2014[J]. Bull. Eng. Geol. Environ.，2015，74：1499-1500.

[98] JAEGER J C. Shear failure of anistropic rocks[J]. Geological Magazine，1960，97( 1 )：65-72.

[99] HUDSON J，HARRISON J，POPESCU M. Engineering rock mechanics：An introduction to the principles[J]. Applied Mechanics Reviews，2002，55( 2 )：72.

[100] CAO R，YAO R，MENG J，et al. Failure mechanism of non-persistent jointed rock-like specimens under uniaxial loading ：Laboratory testing[J]. International Journal of Rock Mechanics and Mining Sciences，2020，132：104341.

[101] INDRARATNA B，PREMADASA W，BROWN E T，et al. Shear strength of rock joints influenced by compacted infill[J]. International Journal of Rock Mechanics and Mining Sciences，2014，70：296-307.

[102] LIU M，LIU E. Dynamic mechanical properties of artificial jointed rock samples subjected to cyclic triaxial loading[J]. International Journal of Rock Mechanics and Mining Sciences，2017，98：54-66.

[103] 潘建武. 含单一天然弱面岩石试样的力学特性研究[D]. 焦作：河南理工大学，2010.PAN Jianwu. Study on the mechanical properties of rock specimens with a single natural weak plane[D]. Jiaozuo：Henan Polytechnic University，2010.

[104] 苏承东，吴秋红. 含天然贯通弱面石灰岩试样的力学性质研究[J].岩石力学与工程学报，2011，30( S2 )：3944-3952.SU Chengdong，WU Qiuhong. Study of mechanical property of limestone specimens with natural continuous weak plane[J]. Chinese Journal of Rock Mechanics and Engineering，2011，30( S2 )：3944-3952.

[105] 杨圣奇，陆家炜，田文岭，等. 不同节理粗糙度类岩石材料三轴压缩力学特性试验研究[J]. 岩土力学，2018，39(S1 )：21-32.YANG Shengqi，LU Jiawei，TIAN Wenling，et al. Experimental study of mechanical behavior of rock specimens with different joint roughness coefficient under conventional triaxial compression[J].Rock and Soil Mechanics，2018，39( S1 )：21-32.

[106] 章颖辉. 含胶结剂结构面力学特性试验研究[D]. 南昌：东华理工大学，2019.ZHANG Yinghui. Experimental study on mechanical properties of structural surface containing cementing agent[D]. Nanchang：East China University of Technology，2019.

[107] ZHANG Y，REN F，ZHAO X. Characterization of joint set effect on rock pillars using synthetic rock mass numerical method[J].International Journal of Geomechanics，2017，17( 3 )：06016026.

[108] 汪子华，熊良宵. 含单节理裂隙岩体的单轴压缩试验及数值模拟[J]. 地质灾害与环境保护，2019，30( 2 )：81-85.WANG Zihua，XIONG Liangxiao. Uniaxial compression test of singlejoint fractured rock mass considering the influence of thickness and length of joint surface and numerical simulation[J]. Journal of Geological Hazards and Environment Preservation，2019，30( 2 )：81-85.

[109] 王学滨. 基于能量原理的岩样单轴压缩剪切破坏失稳判据[J].工程力学，2007，24( 1 )：153-161.WANG Xuebin. Unstable criterion of rock specimen subjected to shear failure in uniaxial compression based on energy principle[J].Engineering Mechanics，2007，24( 1 )：153-161.

[110] 姚再兴，刘向峰，范福平. 单一弱面控制岩石力学系统特性[J].辽宁工程技术大学学报，2001，20( 4 )：533-534.YAO Zaixing，LIU Xiangfeng，FAN Fuping. A single weak plane controlling over the characteristics of the rock-mechanics system[J].Journal of Liaoning Technical University Natural Science Edition，2001，20( 4 )：533-534.

[111] 尤明庆，苏承东. 具有沉积弱面试样的剪切拉伸破坏及强度分析[J]. 岩石力学与工程学报，2006，25( S2 )：3618-3622.YOU Mingqing，SU Chengdong. Analysis of strength and shear-tensile failure of rock specimens with sedimentary weak plane[J]. Chinese Journal of Rock Mechanics and Engineering，2006，25( S2 )：3618-3622.

[112] SINHA S，WALTON G. Investigation of pillar damage mechanisms and rock-support interaction using bonded block models[J]. International Journal of Rock Mechanics and Mining Sciences，2021，138：104652.

[113] MUAKA J，DUMA S，MUSHANGWE P，et al. Modelling hard rock jointed pillars using a distinct element and discrete fracture network approach considering the effect of a clay-filled shear structure[A].Proceedings of the Eighth International Conference on Deep and High Stress Mining[C]. Perth，Australian，2017：311-328.

[114] FARAHMAND K，VAZAIOS I，DIEDERICHS M S，et al. Investigating the scale-dependency of the geometrical and mechanical properties of a moderately jointed rock using a synthetic rock mass ( SRM ) approach[J]. Computers and Geotechnics，2018，95：162-179.

[115] ZHANG Y，ZHAO X. Characterisation of confinement effect on jointed rock pillars using a synthetic rock mass approach[J]. International Journal for Numerical and Analytical Methods in Geomechanics，2016，40( 12 )：1690-1711.

[116] 郭松峰，祁生文，李星星，等. 含结构面岩体试样单轴强度与变形特征[J]. 工程地质学报，2016，24( 5 )：891-898.GUO Songfeng，QI Shengwen，LI Xingxing，et al. Strength and deformation characteristics of rock sample with discontinuities under numerical uniaxial compression simulation tests[J]. Journal of Engineering Geology，2016，24( 5 )：891-898.

[117] GUO S，QI S. Numerical study on progressive failure of hard rock samples with an unfilled undulate joint[J]. Engineering Geology，2015，193：173-182.

[118] 郑青松，刘恩龙，刘明星. 三轴试验下结构面倾角对制备岩样力学特性的影响[J]. 岩土力学，2019，38( 5 )：1854-1861.ZHENG Qingsong，LIU Enlong，LIU Mingxing. Influence of dip angle of structural planes on mechanical properties of artificial rock samples under triaxial test conditions[J]. Rock and Soil Mechanics，2019，38( 5 )：1854-1861.

[119] 冒海军，杨春和. 结构面对板岩力学特性影响研究[J]. 岩石力学与工程学报，2005，24( 20 )：3651-3656.MAO Haijun，YANG Chunhe. Study on effects of discontinuities on mechanical characters of slate[J]. Chinese Journal of Rock Mechanics and Engineering，2005，24( 20 )：3651-3656.

[120] 李宏哲，夏才初，王晓东，等. 含节理大理岩变形和强度特性的试验研究[J]. 岩石力学与工程学报，2008，27( 10 )：2118-2123.LI Hongzhe，XIA Caichu，WANG Xiaodong，et al. Experimental study on deformation and strength properties of jointed marble specimens[J].Chinese Journal of Rock Mechanics and Engineering，2008，27( 10 )：2118-2123.

[121] 范海军，郝艳广，肖盛燮. 岩样直剪应力-应变全程曲线研究[J].岩石力学与工程学报，2006，25( S1 )：2612-2617.FAN Haijun，HAO Yanguang，XIAO Shengxie. Study on complete stress-strain curve of rock specimen under direct shear test[J].Chinese Journal of Rock Mechanics and Engineering，2006，25( S1 )：2612-2617.

[122] 唐志成，夏才初，肖素光. 节理剪切应力-位移本构模型及剪胀现象分析[J]. 岩石力学与工程学报，2011，30( 5 )：917-925.TANG Zhicheng，XIA Caichu，XIAO Suguang. Constitutive model for joint shear stress-displacement and analysis of dilation[J]. Chinese Journal of Rock Mechanics and Engineering，2011，30( 5 )：917-925.

[123] USEFZADEH A，YOUSEFZADEH H，SALARI-RAD H，et al.Empirical and mathematical formulation of the shear behavior of rock joints[J]. Engineering Geology，2013，164：243-252.

[124] BAHAADDINI M，HAGAN P C，MITRA R，et al. Experimental and numerical study of asperity degradation in the direct shear test[J].Engineering Geology，2016，204：41-52.

[125] JOHANSSON F. Influence of scale and matedness on the peak shear strength of fresh，unweathered rock joints[J]. International Journal of Rock Mechanics and Mining Sciences，2016，82：36-47.

[126] MENG F，ZHOU H，LI S，et al. Shear behaviour and acoustic emission characteristics of different joints under various stress levels[J]. Rock Mechanics and Rock Engineering，2016，49( 12 )：4919-4928.

[127] ZHANG G，KARAKUS M，TANG H，et al. Estimation of joint roughness coefficient from three-dimensional discontinuity surface[J].Rock Mechanics and Rock Engineering，2017，50( 9 )：2535-2546.

[128] 陈世江，朱万成，王创业，等. 岩体结构面粗糙度系数定量表征研究进展[J]. 力学学报，2017，49( 2 )：239-256.CHEN Shijiang，ZHU Wancheng，WANG Chuangye，et al. Review of research progresses of the quantifying joint roughness coefficient[J].Chinese Journal of Theoretical and Applied Mechanics，2017，49( 2 )：239-256.

[129] XIA C C，TANG Z C，XIAO W M，et al. New peak shear strength criterion of rock joints based on quantified surface description[J].Rock Mechanics and Rock Engineering，2013，47( 2 )：387-400.

[130] DONG H，GUO B，LI Y，et al. Empirical formula of shear strength of rock fractures based on 3D morphology parameters[J]. Geotechnical and Geological Engineering，2017，35( 3 )：1169-1183.

[131] MENG F，WONG L N Y，ZHOU H，et al. Comparative study on dynamic shear behavior and failure mechanism of two types of granite joint[J]. Engineering Geology，2018，245：356-369.

[132] 唐志成，夏才初，黄继辉，等. 节理峰值后归一化位移软化模型[J].岩土力学，2011，32( 7 )：2013-2016.TANG Zhicheng，XIA Caichu，HUANG Jihui，et al. Post-peak normalized displacement softening model for discontinuous rock joint[J]. Rock and Soil Mechanics，2011，32( 7 )：2013-2016.

[133] 王水林，郭明伟，王万军，等. 节理面剪切应力-切向位移曲线峰值后区特性的初步研究[J]. 岩石力学与工程学报，2016，35(S2 )：3805-3812.WANG Shuilin，GUO Mingwei，WANG Wanjun，et al. A preliminary study of the post-peak characteristics of shear stress-displacement curves of joints[J]. Chinese Journal of Rock Mechanics and Engineering，2016，35(S2 )：3805-3812.

[134] GOODMAN R E. A model for the mechanics of jointed rock[J].Journal of the Soil Mechanics & Foundations Division，1968，94：637-660.

[135] SAEB S，AMADEI B. Modelling rock joints under shear and normal loading[J]. International Journal of Rock Mechanics and Mining Sciences Geomechanics Abstracts，1992，29( 3 )：267-278.

[136] PARK J W，LEE Y K，SONG J J，et al. A constitutive model for shear behavior of rock joints based on three-dimensional quantification of joint roughness[J]. Rock Mechanics and Rock Engineering，2013，46( 6 )：1513-1537.

[137] POUYA A，YAZDI P B. A damage-plasticity model for cohesive fractures[J]. International Journal of Rock Mechanics & Mining Sciences，2015，73：194-202.

[138] SIMON R，AUBERTIN M，MITRI H. A non-linear constitutive model for rock joints to evaluate unstable slip[C]. The 37th US Symposium on Rock Mechanics ( USRMS )，Colorado，1999.

[139] AMADEI B，WIBOWO J，STURE S，et al. Applicability of existing models to predict the behavior of replicas of natural fractures of welded tuff under different boundary conditions[J]. Geotechnical & Geological Engineering，1998，16( 2 )：79-128.

[140] GRASSELLI G，EGGER P. Constitutive law for the shear strength of rock joints based on three-dimensional surface parameters[J].International Journal of Rock Mechanics and Mining Sciences，2003，40( 1 )：25-40.

[141] PLESHA M E. Constitutive models for rock discontinuities with dilatancy and surface degradation[J]. International Journal for Numerical and Analytical Methods in Geomechanics，2010，11( 4 )：345-362.

[142] 徐磊，任青文. 岩体结构面新型本构模型研究[J]. 岩土力学，2011，32( S1 )：217-224.XU Lei ，REN Qingwen. A new constitutive model for rock discontinuities[J]. Rock and Soil Mechanics，2011，32( S1 )：217-224.

[143] 方理刚. 岩石节理弹塑性本构关系[J]. 岩土工程学报，1996，18( 3 )：91-95.FANG Ligang. Elastoplastic constitutive relation of rock joints[J].Chinese Jounal of Geotechnical Engineering，1996，18( 3 )：91-95.

[144] CORDING E J，HASHASH Y M A，OH J. Analysis of pillar stability of mined gas storage caverns in shale formations[J]. Engineering Geology，2015，184：71-80.

[145] ZHANG J，HUANG P，ZHANG Q，et al. Stability and control of room mining coal pillars-taking room mining coal pillars of solid backfill recovery as an example[J]. Journal of Central South University，2017，24( 5 )：1121-1132.

[146] 付建新，宋卫东，杜建华. 金属矿山采空区群形成过程中围岩扰动规律研究[J]. 岩土力学，2013，34( S1 )：508-515.FU Jianxin，SONG Weidong，DU Jianhua. Study of disturbance law for wall rock while goaf group formation in metal mines[J]. Rock and Soil Mechanics，2013，34( S1 )：508-515.

[147] ZIPF R K. Simulation of cascading pillar failure in room-and-pillar mines using boundary-element-method[A]. 2nd North American Rock Mechanics Symposium[C]. Montreal，Quebec，Canada：American Rock Mechanics Association，1996：6.

[148] 何江. 煤矿采动动载对煤岩体的作用及诱冲机理研究[D]. 徐州：中国矿业大学，2013.HE Jiang. Research of mining dynamic loading effect and its induced rock burst in coal mine[D]. Xuzhou：China University of Mining and Technology，2013.

[149] BLAKE W，LEIGHTON F，DUVALL W I. Microseismic techniques for monitoring the behavior of rock structures[R]. Washington D C：United States Government Printing Office，1974.

[150] 牟宗龙，窦林名，张广文，等. 坚硬顶板型冲击矿压灾害防治研究[J]. 中国矿业大学学报，2006，35( 6 )：737-741.MOU Zonglong，DOU Linming，ZHANG Guangwen，et al. Study of prevention methods of rock burst disaster caused by hard rock roof[J].Journal of China University of Mining & Technology，2006，35( 6 )：737-741.

[151] 陈璐. 多矿柱体系承载特性与失稳机理研究[D]. 长沙：中南大学，2018.CHEN Lu. Study on loading characteristics and failure mechanism of multiple pillar system[D]. Changsha：Central South University，2018.

[152] ZIPF R K. Toward pillar design to prevent collapse of room and pillar mines[R]. Spokane，W A：NIOSH-Spokane Research Laboratory，2011.

[153] SWANSON P L，BOLER F M. The magnitude 5.3 seismic event and collapse of the solvay trona mine：Analysis of pillar/floor failure stability[R]. United States Bureau of Mines Open Fire Report，1995：86-95.

[154] ESTERHUIZEN G S，TYRNA P L，MURPHY M M. A case study of the collapse of slender pillars affected by through-going discontinuities at a limestone mine in Pennsylvania[J]. Rock Mechanics and Rock Engineering，2019，52( 12 )：4941-4952.

[155] 王金安，赵志宏，侯志鹰. 浅埋坚硬覆岩下开采地表塌陷机理研究[J]. 煤炭学报，2007，32( 10 )：1051-1056.WANG Jin'an ，ZHAO Zhihong ，HOU Zhiying. Study on the catastrophic collapse of surface land induced by mining under a shallow and hard strata[J]. Journal of China Coal Society，2007，32( 10 )：1051-1056.

[156] 李俊平. 缓倾斜采空场处理新方法及采场地压控制研究[D]. 北京：北京理工大学，2003.LI Junping. Study of new disposing method and ground pressure control for gently inclined abandoned stope[D]. Beijing：Beijing Institute of Technology，2003.

[157] LI C，XU J ，WANG Z，et al. Domino instability effect of surrounding rock-coal pillars in a room-and-pillar gob[J]. International Journal of Mining Science and Technology，2013，23( 6 )：913-918.

[158] ZHOU Z，WANG H，CAI X，et al. Bearing characteristics and fatigue damage mechanism of multi-pillar system subjected to different cyclic loads[J]. Journal of Central South University，2020，27( 2 )：542-553.

[159] ZHU D，SONG X，LI H，et al. Cooperative load-bearing characteristics of a pillar group and a gob pile in partially caved areas at shallow depth[J]. Energy Science and Engineering，2020，8( 1 )：89-103.

[160] ZHOU Z，ZANG H，CAO W，et al. Risk assessment for the cascading failure of underground pillar sections considering interaction between pillars[J]. International Journal of Rock Mechanics and Mining Sciences，2019，124：104142.

[161] ZHU W，CHEN L，ZHOU Z，et al. Failure propagation of pillars and roof in a room and pillar mine induced by longwall mining in the lower seam[J]. Rock Mechanics and Rock Engineering，2019，52( 4 )：1193-1209.

[162] ZHOU Z，CHEN L，CAI X，et al. Experimental investigation of the progressive failure of multiple pillar-roof system[J]. Rock Mechanics and Rock Engineering，2018，51( 5 )：1629-1636.

[163] 邓高，杨珊. 基于组合预测与变精度粗糙模糊集的采空区稳定性评价[J]. 黄金科学技术，2017，25( 3 )：98-107.DENG Gao，YANG Shan. Stability evaluation of goafs based on combined forecasting and variable precision rough fuzzy set[J]. Gold Science and Technology，2017，25( 3 )：98-107.

[164] 郝旭彬，杨立辉，万胜. 基于AHP及模糊综合评判法的采空区稳定性评价[J]. 黄金科学技术，2013，21( 6 )：63-67.HAO Xubin，YANG Lihui，WAN Sheng. Stability evaluation for mine gob areas based on ahp and fuzzy synthetic judgement theory[J]. Gold Science and Technology，2013，21( 6 )：63-67.

[165] HUANG Z，DAI X，DONG L. Buckling failures of reserved thin pillars under the combined action of in-plane and lateral hydrostatic compressive forces[J]. Computers & Geotechnics，2017，87( 7 )：128-138.

[166] 张耀平，曹平，袁海平，等. 复杂采空区稳定性数值模拟分析[J].采矿与安全工程学报，2010，27( 2 )：233-238.ZHANG Yaoping，CAO Ping，YUAN Haiping，et al. Numerical simulation on stability of complicated goaf[J]. Journal of Mining &Safety Engineering，2010，27( 2 )：233-238.

[167] 方勇，姚志刚，符亚鹏，等. 上覆水平煤层采空区衬砌受荷模型试验研究[J]. 岩土工程学报，2016，38( 8 )：1513-1521.FANG Yong，YAO Zhigang，FU Yapeng，et al. Model tests on loading characteristics of linings in overlying horizontal coal mined-out area[J].Chinese Journal of Geotechnical Engineering，2016，38( 8 )：1513-1521.

[168] 胡静云，李庶林，林峰，等. 特大采空区上覆岩层地压与地表塌陷灾害监测研究[J]. 岩土力学，2014，35( 4 )：1117-1122.HU Jingyun，LI Shulin，LIN Feng，et al. Research on disaster monitoring of overburden ground pressure and surface subsidence in extra-large mined-out area[J]. Rock and Soil Mechanics，2014，35( 4 )：1117-1122.

[169] 宋卫东，付建新，杜建华，等. 基于精密探测的金属矿山采空区群稳定性分析[J]. 岩土力学，2012，33( 12 )：3781-3787.SONG Weidong，FU Jianxin，DU Jianhua，et al. Analysis of stability of goaf group in metal mines based on precision detection[J]. Rock and Soil Mechanics，2012，33( 12 )：3781-3787.

[170] 周子龙，李夕兵，赵国彦. 民窿空区群级联失稳评价[J]. 自然灾害学报，2007，16( 5 )：91-95.ZHOU Zilong，LI Xibing，ZHAO Guoyan. Evaluation of cascading collapse for private mined zone groups[J]. Journal of Natural Disasters，2007，16( 5 )：91-95.

[171] POULSEN B A ，SHEN B. Subsidence risk assessment of decommissioned bord-and-pillar collieries[J]. International Journal of Rock Mechanics and Mining Sciences，2013，60：312-320.

[172] 李令鑫. 基于类框架结构模型的采空区群失稳研究[D]. 广州：华南理工大学，2017.LI Lingxin. Research on instability of goaf group based on the framelike structure model[D]. Guangzhou：South China University of Technology，2017.

[173] 王国伟. 基于框架结构法的采空区群失稳响应及控制研究[D].广州：华南理工大学，2017.WANG Guowei. Research on instability response and control technology of goaf group based on the frame structure method[D].Guangzhou：South China University of Technology，2017.

[174] ZHOU Z，ZHAO Y，CAO W，et al. Dynamic response of pillar workings induced by sudden pillar recovery[J]. Rock Mechanics and Rock Engineering，2018，51( 10 )：3075-3090.

[175] 柯昌涛. 矿柱连锁失稳过程中的载荷传递及连锁失稳灾害的风险评价[D]. 长沙：中南大学，2018.KE Changtao. Risk assessment of load transfer and chain instability disasters in the process of cascading pillar failure[D]. Changsha：Central South University，2018.

[176] 赵源. 地下岩柱承载与失稳的诱发动力机制[D]. 长沙：中南大学，2017.ZHAO Yuan. Induced dynamic mechanism of bearing and instability of underground rock pillar[D]. Changsha：Central South University，2017.

[177] 陈庆发. 隐患资源开采与采空区治理协同研究[D]. 长沙：中南大学，2009.CHEN Qingfa. Study on synergism of hidden danger resources mining and goafs treatment[D]. Changsha：Central South University，2009.

[178] KAISER P K，TANG C A. Numerical simulation of damage accumulation and seismic energy release during brittle rock failure Part II：Rib pillar collapse[J]. International Journal of Rock Mechanics and Mining Sciences，1998，35( 2 )：123-134.

[179] WANG S Y，SLOAN S W，HUANG M L，et al. Numerical study of failure mechanism of serial and parallel rock pillars[J]. Rock Mechanics and Rock Engineering，2011，44( 2 )：179-198.

[180] GAO F，KANG H，LOU J，et al. Evolution of local mine stiffness with mining process：Insight from physical and numerical modeling[J].Rock Mechanics and Rock Engineering，2019，52( 10 )：3947-3958.

[181] STARFIELD A M，FAIRHURST C. How high-speed computers advance design of practical mine pillar systems[J]. Engng. Min. J.，1968，169( 5 )：78-84.

[182] JAISWAL A，SHRIVASTVA B K. Stability analysis of the proposed hybrid method of partial extraction for underground coal mining[J].International Journal of Rock Mechanics and Mining Sciences，2012，52：103-111.

[183] MANDAL P K，DAS A J. Prediction of coal bump with respect to local mine stiffness and post-failure stiffness using numerical modelling[J].Journal of Mines, Metals and Fuels，2018，66( 6 )：328-338.

[184] ZIPF R K. Analysis of stable and unstable pillar failure using a local mine stiffness method[A]. Proceedings of the Workshop on Coal Pillar Mechanics and Design[C]. Washington D C，United States，1992：128-143.

[185] KIAS E. Investigation of unstable failure in underground coal mining using the discrete element method[J]. Dissertations & Theses-Gradworks，2013.

[186] GU R，OZBAY U. Numerical investigation of unstable rock failure in underground mining condition[J]. Computers and Geotechnics，2015，63：171-182.

[187] LACHENICHT R. Relationship between ERR，system stiffness parameters and seismic energy release for different geotechnical areas[R]. SIMRAC Final Report GAP612a，2001.

[188] XU Shuai，LIU Jianpo，XU Shida，et al. Experimental studies on pillar failure characteristics based on acoustic emission location technique[J]. Transactions of Nonferrous Metals Society of China，2012，22( 11 )：2792-2798.

[189] 周子龙，陈璐，赵源，等. 双矿柱体系变形破坏及承载特性的试验研究[J]. 岩石力学与工程学报，2017，36( 2 )：420-428.ZHOU Zilong，CHEN Lu，ZHAO Yuan，et al. Experimental study on failure mechanism and bearing characteristic of double-pillar system[J]. Chinese Journal of Rock Mechanics and Engineering，2017，36( 2 )：420-428.

[190] ZHOU Z，CHEN L，ZHAO Y，et al. Experimental and numerical investigation on the bearing and failure mechanism of multiple pillars under overburden[J]. Rock Mechanics and Rock Engineering，2017，50( 4 )：995-1010.

[191] DONG H，ZHU W，HOU C，et al. Load transfer behavior during cascading pillar failure：an experimental study[J]. Rock Mechanics and Rock Engineering，2022，55( 3 )：1445-1460.

[192] 陈伟. 采空区群顶板动静稳定性研究[D]. 赣州：江西理工大学，2019.CHEN Wei. Study on dynamic and static stability of goaf group roof[D]. Ganzhou：Jiangxi University of Science and Technology，2019.

[193] 吴亚斌. 基于CMS实测的采空区群稳定性数值模拟研究[D]. 长沙：中南大学，2007.WU Yabin. Numerical simulation method for mined-out area group stability based on cavity monitoring system[D]. Changsha：Central South University，2007.

[194] 罗周全，鹿浩，刘晓明，等. 基于CMS实测的采空区群稳定性数值模拟方法[J]. 化工矿物与加工，2008，37( 1 )：18-21.LUO Zhouquan，LU Hao，LIU Xiaoming，et al. Numerical simulation method for mined-out area group stability based on cavity monitoring system[J]. Industrial Minerals & Processing，2008，37( 1 )：18-21.

[195] 刘超，杨仕教，王洪武，等. 五道岭钼矿大规模采空区群失稳复活的数值模拟[J]. 现代矿业，2011，28( 3 )：6-8.LIU Chao，YANG Shijiao，WANG Hongwu，et al. Numerical simulation on the instability and resurrection of large-scale mined-out area in Wudaoling Molybdenum Mine[J]. Modern Mining，2011，28( 3 )：6-8.

[196] HAUQUIN T，DECK O，GUNZBURGER Y. Average vertical stress on irregular elastic pillars estimated by a function of the relative extraction ratio[J]. International Journal of Rock Mechanics and Mining Sciences，2016，83：122-134.

[197] 周子龙，柯昌涛，王亦凡，等. 基于颗粒离散元的矿柱群连锁失稳机理分析[J]. 中国地质灾害与防治学报，2018，29( 4 )：78-84.ZHOU Zilong，KE Changtao，WANG Yifan，et al. Mechanism of pillar's cascading failure based on discrete particle flow code[J].Chinese Journal of Geological Hazard and Control，2018，29( 4 )：78-84.

[198] WANG F，KAUNDA R. Assessment of rockburst hazard by quantifying the consequence with plastic strain work and released energy in numerical models[J]. International Journal of Mining Science and Technology，2019，29( 1 )：93-97.

[199] 吴启红，万世明，彭文祥. 一种多层采空区群稳定性的综合评价法[J]. 中南大学学报( 自然科学版 )，2012，43( 6 )：2324-2330.WU Qihong，WAN Shiming，PENG Wenxiang. A comprehensive evaluation method about stability of polylaminate goafs[J]. Journal of Central South University( Science and Technology )，2012，43( 6 )：2324-2330.

[200] 刘晓明，罗周全，杨承祥，等. 基于实测的采空区稳定性数值模拟分析[A]. 全国岩土力学数值分析与解析方法研讨会[C].武汉，2007：521-526.LIU Xiaoming，LUO Zhouquan，YANG Chengxiang，et al. Analysis of stability of cavity based on cavity monitoring[C]. Proceeding on Numerical Analysis and Analytical Methods of Geotechnical Mechanics[C]. Wuhan，2007：521-526.

[201] 付建新，宋卫东，杜建华. 金属矿山采空区群形成过程中围岩扰动规律研究[A]. 第十三届全国岩石动力学学术会议[C]. 重庆，2013：508-515.FU Jianxin，SONG Weidong，DU Jianhua. Study on the law of surrounding rock disturbance in the formation of goaf groups in metal mines[A]. The 13th National Academic Conference on Rock Dynamics[C]. Chongqing，2013：508-515.

[202] 姜立春，罗恩民，贾晓川. 纵向采空区群失稳动态演化过程研究[J]. 矿业研究与开发，2017，37( 4 )：62-65.JIANG Lichun，LUO Enmin，JIA Xiaochuan. Study on dynamic failure process of longitudinal goaf group[J]. Mining Research and Development，2017，37( 4 )：62-65.

[203] 姜立春，曾俊佳，贾晓川. 水平采空区群动态失稳演化过程及工程控制[J]. 辽宁工程技术大学学报(自然科学版)，2016，35( 8 )：821-825.JIANG Lichun，ZENG Junjia，JIA Xiaochuan. Dynamic failure process and engineering control of horizontal goaf group[J]. Journal of Liaoning Technical University ( Natural Science )，2016，35( 8 )：821-825.

[204] 陈柘儒. 矿柱支撑系统应力扰动响应及稳定性分析[D]. 青岛：山东科技大学，2018.CHEN Zheru. Response regular and stability analysis of stress disturbance in pillar support system[D]. Qingdao：Shandong University of Science and Technology，2018.

[205] 胡高建，杨天鸿，张飞，等. 红岭铅锌矿多中段回采围岩破坏机理研究[J]. 金属矿山，2017，46( 9 )：20-24.HU Gaojian，YANG Tianhong，ZHANG Fei，et al. Study on the surrounding rock failure mechanism in muti-level stoping in Hongling Pb-Zn Mine[J]. Metal Mine，2017，46( 9 )：20-24.

[206] 赵永，杨天鸿，解联库，等. 红岭铅锌矿的虚拟现实系统[J]. 金属矿山，2015，44( 1 )：98-103.ZHAO Yong，YANG Tianhong，XIE Lianku，et al. Hongling Lead-zinc Mine's virtual reality technology[J]. Metal Mine，2015，44( 1 )：98-103.

[207] 赵永，杨天鸿，王薪荣，等. 基于Mathews稳定图法的采空区稳定性评价[J]. 东北大学学报( 自然科学版 )，2016，37( 1 )：74-78.ZHAO Yong，YANG Tianhong，WANG Xinrong，et al. Stability evaluation of stope based on mathews graph method[J]. Journal of Northeastern University( Natural Science )，2016，37( 1 )：74-78.