力学-电化学交互作用下E690钢的腐蚀疲劳裂纹扩展速率理论模型

2022-08-03马剑军

机械工程材料 2022年6期

马剑军，刘肖，王恒

(1.上海振华重工集团(南通)传动机械有限公司，南通 226017；2.南通大学机械工程学院，南通 226019)

0 引言

在国家实施海洋强国战略的环境下，海洋工程装备受到广泛的关注[1]。E690高强钢因具有高强度、良好的韧性、优异的抗疲劳和耐腐蚀性等特点，而广泛应用于海洋工程装备中[2-3]。海洋工程装备的工作环境恶劣，腐蚀疲劳问题成为该装备服役过程中不可忽视的问题，研究海洋工程装备材料的腐蚀疲劳特性便显得尤为重要。腐蚀疲劳损伤是腐蚀损伤与疲劳损伤耦合作用的结果，也是腐蚀因素、疲劳因素以及材料自身因素共同影响的结果[4]。影响E690高强钢腐蚀疲劳特性的疲劳因素包括应力比、应力幅、加载频率以及加载波形等[5]，腐蚀因素包括pH、温度、含氧量、氯化物含量以及干湿条件等[6]，材料自身因素包括化学成分、组织、性能以及缺陷等。目前，有关E690高强钢的研究主要集中在力学性能、显微组织、焊接性能以及热处理工艺等方面[7-8]。在腐蚀特性方面，郝文魁[2]、马宏驰等[9]通过干湿交替环境模拟海洋薄液环境来研究E690高强钢的腐蚀行为及机理。但是，目前还未见有关E690高强钢腐蚀疲劳裂纹扩展理论模型的研究报道。

腐蚀疲劳特性对材料的影响主要表现在腐蚀疲劳裂纹扩展速率上，目前描述材料腐蚀疲劳裂纹扩展速率的理论模型主要有叠加模型、竞争模型以及基于Paris公式修正的模型[10]。由于材料腐蚀疲劳性能以及腐蚀环境具有一定的差异性，腐蚀疲劳裂纹扩展速率理论模型不具备良好的通用性。在工程实践中，对于材料腐蚀疲劳裂纹扩展速率的研究主要是通过试验来修正Paris公式得到模型(简称Paris模型)，例如引入环境因子与疲劳载荷因子，基于试验数据得到因子的表达式，研究不同腐蚀和疲劳因素对其腐蚀疲劳裂纹扩展速率的影响[11]。但是建立Paris模型需要大量的试验数据，试验数据的准确性影响着模型的可靠性，从而影响腐蚀疲劳裂纹扩展速率预测的准确性，继而影响寿命预测的准确性。Paris模型仅反映裂纹扩展速率的平均水平，并不能体现极端情况下的裂纹扩展速率；同时，Paris模型无法反映应力比、频率以及应力幅等因素对材料腐蚀疲劳裂纹扩展行为的具体影响。

依据能量守恒原则建立的模型可以避免出现上述需要大量试验数据，不能反映极端情况，无法反映应力比、频率以及应力幅影响的问题[12]。作者通过研究腐蚀疲劳裂纹扩展过程中能量的变化并推导各种能量的表达式，依据能量守恒原则建立E690高强钢的腐蚀疲劳裂纹扩展速率理论模型，同时对E690高强钢进行腐蚀疲劳裂纹扩展试验，计算出腐蚀疲劳裂纹扩展速率，通过理论模型计算结果与试验结果的对比，验证该理论模型的准确性，以期为E690高强钢的腐蚀疲劳寿命预测提供理论指导。

1 试样制备与试验方法

按照GB/T 6398-2000，截取如图1所示的腐蚀疲劳裂纹扩展试样，对试样进行裂纹预制，预制裂纹长度为2 mm,采用SCHENCK160M型电液伺服疲劳试验机进行腐蚀疲劳裂纹扩展试验，研究腐蚀环境及应力比对其裂纹扩展行为的影响。选取正弦波形加载方式，试验频率为10 Hz，具体的试验参数如表1所示。按照HB 6266-1992配置质量分数3.5% NaCl溶液模拟海水。试验过程中测量裂纹长度，试验结束后将试样放入干燥器中保存。

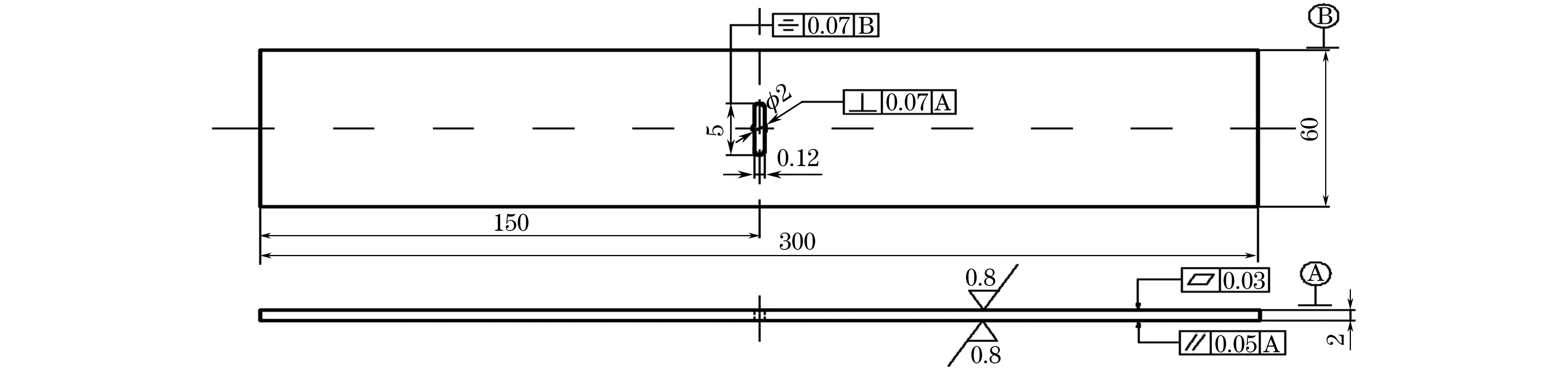
图1 E690高强钢腐蚀疲劳裂纹扩展试样的尺寸Fig.1 Size of corrosion fatigue crack growth specimen of E690 high strength steel

2 试验结果与讨论

不同试验条件下E690高强钢的裂纹长度-循环次数曲线(a-N曲线)如图2所示。由图2可知：在相同应力比下，E690高强钢在质量分数3.5% NaCl溶液中的疲劳寿命比在空气中低很多，即在较少的循环次数作用下该钢发生断裂；应力比的增大会促使该钢较早断裂，疲劳寿命降低。腐蚀疲劳裂纹扩展行为是力学与电化学交互作用的结果。电化学对裂纹扩展的促进作用会明显降低试样的寿命，使试样较早发生断裂失效。

图2 不同试验条件下E690高强钢的a-N曲线 Fig.2 a-N curves of E690 high strength steel under differenttest conditions

通过对试验数据处理，得到疲劳裂纹扩展速率(da/dN)和应力强度因子范围(ΔK)的散点图。由图3可知，腐蚀环境对E690高强钢裂纹扩展的加速作用主要体现在裂纹扩展初期，对裂纹扩展中后期的作用不明显。由图4可以看出，在质量分数3.5%NaCl溶液中腐蚀疲劳裂纹扩展速率随着应力比的增大而提高，在裂纹扩展初期，应力比为0.5的裂纹扩展速率接近于应力比为0.3的2倍，同时应力比的提高还会降低裂纹扩展的门槛值。

表1 E690高强钢腐蚀疲劳裂纹扩展试验参数

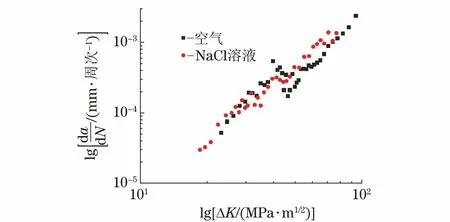
图3 应力比0.1下E690高强钢在空气与质量分数3.5%NaCl溶液中的裂纹扩展速率散点图Fig.3 Scatter plot of crack growth rate of E690 high strength steelin air and 3.5wt% NaCl solution at stress ratio of 0.1

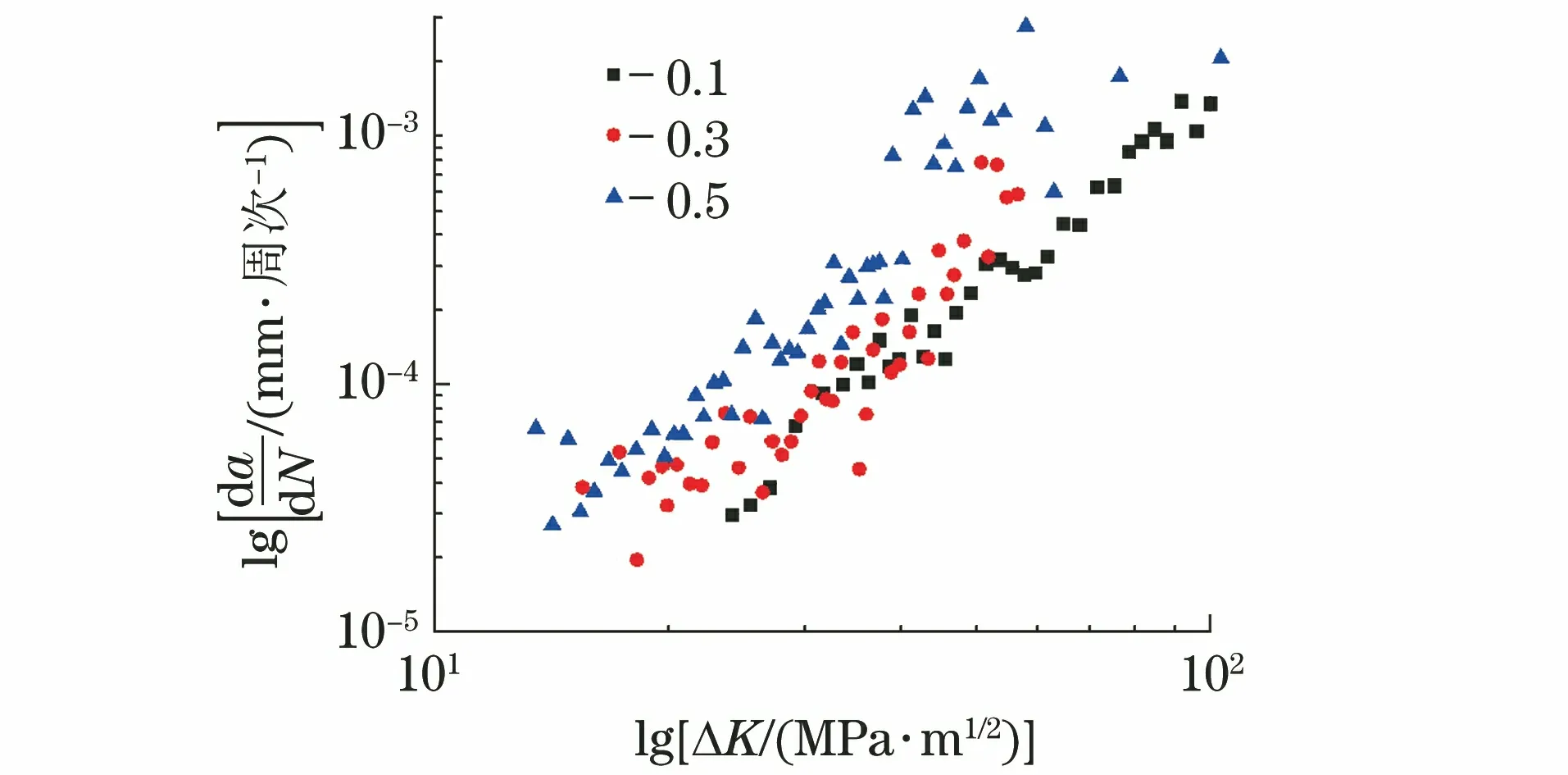
图4 不同应力比下E690高强钢在质量分数3.5%NaCl溶液中的裂纹扩展速率散点图Fig.4 Scatter plot of crack growth rate of E690 high strength steelin 3.5wt% NaCl solution at different stress ratio

3 基于能量守恒的腐蚀疲劳裂纹扩展速率建模

3.1 腐蚀疲劳裂纹扩展过程中的能量方程

根据热力学基本原理，腐蚀疲劳裂纹扩展过程是一个不可逆的过程，其本质是能量转换的过程。E690高强钢腐蚀疲劳裂纹扩展过程中的能量主要包括电化学能、动能和势能。电化学能是E690高强钢在电化学腐蚀过程中阳极溶解所释放的能量，在腐蚀中占主要部分，因此采用电化学能代表腐蚀过程中的能量。动能和势能属于疲劳载荷因素方面的能量。

根据电化学原理，电化学腐蚀过程中阳极溶解释放的电化学能为腐蚀溶解金属所携带电量在电场中所作的功[3]。溶解金属所携带的电量ΔQ表达式[3]为

2exp(-λTZ0)+exp[-λ(TZ-TZ0)]}

(1)

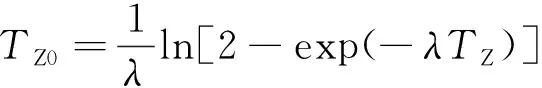
(2)

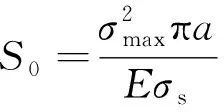
(3)

式中:i0为阳极溶解电流密度；S0为裂纹尖端新露出的金属面积；ρ为材料的密度；λ为形膜速率常数；TZ为疲劳载荷周期；E为材料的弹性模量；σs为材料的屈服强度；σmax为最大应力；TZ0为裂纹扩展后的疲劳载荷周期。

阳极溶解释放的电化学能uc的表达式为

2exp(-λTZ0)+exp[-λ(TZ-TZ0)]}

(4)

式中：E0为腐蚀电池电动势；E⊕为标准电极电位；R为气体常数；T为热力学温度；n为原子价；F为法拉第常数；aMn+为金属离子活度。

在裂纹扩展过程中，载荷的往复作用使得运动微裂纹具有相应的动能。交变载荷作用下的裂纹扩展动能公式修正如下[13]：

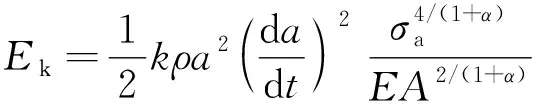
(5)

式中：Ek为裂纹扩展动能；k为与材料相关的常数，对于金属材料取5.45；t为裂纹扩展时间；α为硬化指数，取1；A为硬化系数,A=E；σa为应力幅。

根据位错理论[12,14]，势能由表面能、弹性应变能、位错挤入裂纹所作的功以及位错本身的弹性能组成，势能U的表达式如下：

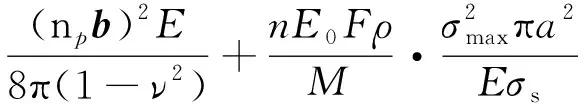
(6)

式中：GIC为临界裂纹扩展力；ν为泊松比；np为位错数；b为柏氏矢量；M为摩尔质量。

3.2 模型的建立

在腐蚀疲劳裂纹扩展过程中，E690高强钢的电化学能、动能和势能都会发生变化，但遵循能量守恒定理，即在一个疲劳载荷作用周期内，裂纹扩展过程中的电化学能、动能和势能总和Φ不变[12]，由此可得：

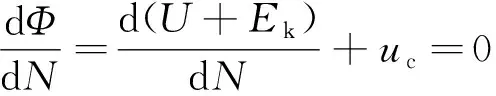
(7)

将势能、动能和电化学能的公式代入式(7)中，并根据da/dt=fda/dN(f为几何修正因子)，得到E690高强钢在腐蚀疲劳环境下的裂纹扩展动力学方程为

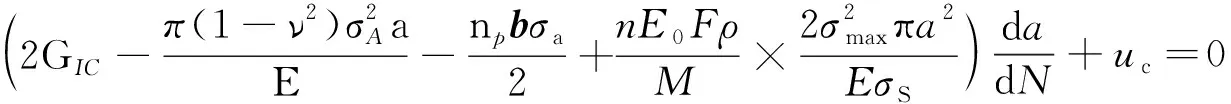
(8)

在裂纹扩展初期和裂纹稳定扩展时期，d2a/dN2与(da/dN)3项非常小，可以忽略[14]，因此裂纹扩展速率da/dN的表达式为

(9)

每个应力循环周期内裂纹尖端增加的位错数d(npb)/dN等于2个滑移面放出的位错数[14]，即：

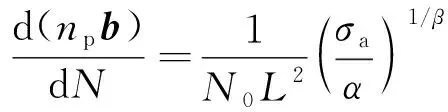
(10)

式中：β为交变应变硬化指数；N0为单位体积内位错源的平均数；L为滑移面的平均长度；α为硬化指数。

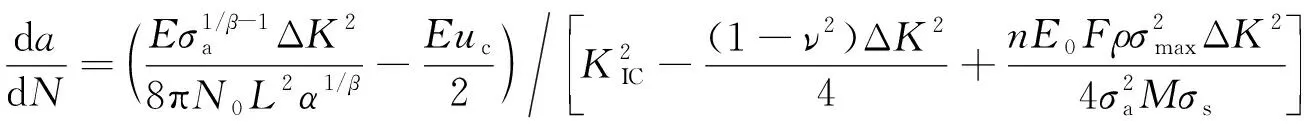
(11)

3.3 模型相关参数的确定

断裂韧性是材料抵抗裂纹扩展的性能，是材料的固有属性，由于缺乏E690高强钢断裂韧性相关的数据资料，作者根据GB/T 4161-2007中的断裂韧度进行测试，试样为标准紧凑型拉伸试样，尺寸如图5所示，试样的起始裂纹采用预制的方法制备。

若满足(Pmax/PQ)≤1.1(Pmax为试验最大载荷，PQ为特定力)以及2.5(KQ/Rp0.2)2(Rp0.2为非比例延伸率为0.2%时的延伸强度，即屈服强度，KQ为断裂韧性)小于试样厚度、裂纹长度和韧带尺寸的要求，则此时KQ等于KIC，否则试验无效。KQ的计算公式

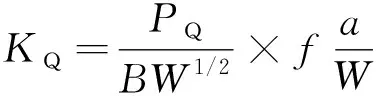
(12)

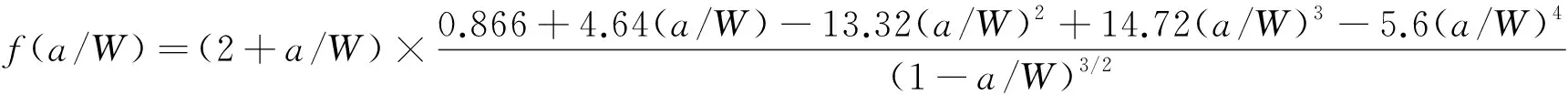
(13)

式中：B为试样厚度；W为试样宽度。

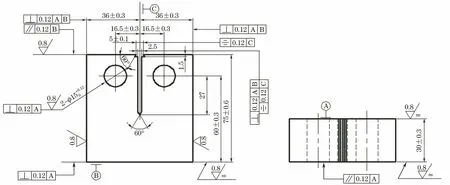
图5 E690高强钢标准紧凑型拉伸试样的尺寸Fig.5 Size of standard compact tensile specimen of E690 high strength steel

断裂韧性试验分两组，试验温度为室温27 ℃，相对湿度为46%，试验参数及试验结果如表2所示。E690高强钢的断裂韧度取两组数值的平均值，即KIC=182.4 MPa·m1/2。

表2 E690高强钢在室温中断裂韧性试验数据

在质量分数3.5% NaCl溶液中E690高强钢的腐蚀疲劳裂纹扩展模型的相关参数如表3,4[15]所示。

表3 在质量分数3.5% NaCl溶液中E690高强钢腐蚀疲劳裂纹扩展模型相关材料参数

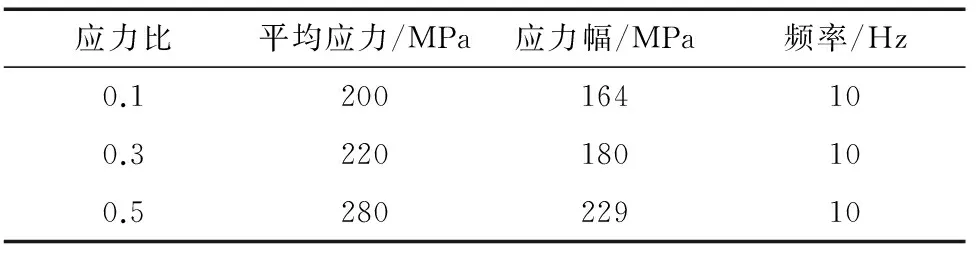
表4 E690高强钢腐蚀疲劳裂纹扩展模型相关试验参数

4 模型验证

将利用理论模型计算得到的E690高强钢在质量分数3.5% NaCl溶液中的腐蚀疲劳裂纹扩展速率与试验结果进行对比。由图6可以看出：由理论模型计算得到的不同应力比下E690高强钢在质量分数3.5% NaCl溶液中的腐蚀疲劳裂纹扩展速率与试验结果基本吻合，相对误差小于10%，腐蚀疲劳裂纹扩展速率随着裂纹尖端应力强度因子范围的增加而变大。由此可知，作者建立的E690高强钢腐蚀疲劳裂纹扩展理论模型能够比较准确地模拟E690高强钢的腐蚀疲劳裂纹扩展行为。

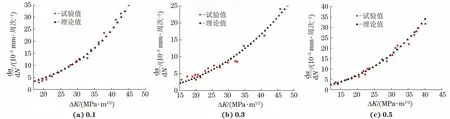
图6 不同应力比下由理论模型计算得到E690高强钢在质量分数3.5% NaCl溶液中的腐蚀疲劳裂纹扩展速率与试验结果的对比Fig.6 Comparison between corrosion fatigue crack growth rate of E690 high strength steel in 3.5wt% NaCl solution calculatedby theoretical model and experimental results at different stress ratio

将E690高强钢裂纹扩展速率理论模型计算结果与Paris模型计算结果进行对比，结果如图7所示。由图7可知，作者建立的理论模型与Paris模型计算得到疲劳裂纹扩展速率-应力强度因子范围拟合直线的斜率与截距几乎接近，即理论模型所计算出的裂纹扩展速率与门槛值均接近，二者的相对误差小于10%。裂纹扩展可分为3个阶段，即裂纹萌生、稳态扩展和快速扩展，其中：裂纹的萌生和稳态扩展是疲劳寿命的主要部分；当裂纹进入快速扩展阶段，预示着构件即将发生断裂失效。研究裂纹扩展的意义在于对构件进行有效预警和寿命预测，预测裂纹扩展速率是研究剩余寿命的一个重要方法。由于裂纹快速扩展阶段只占疲劳寿命的一小部分，在工程实践中，构件的断裂失效预警应在裂纹扩展即将进入快速扩展时进行。此外，在腐蚀疲劳裂纹快速扩展阶段，裂纹扩展的影响因素具有明显的复杂性和不确定性。

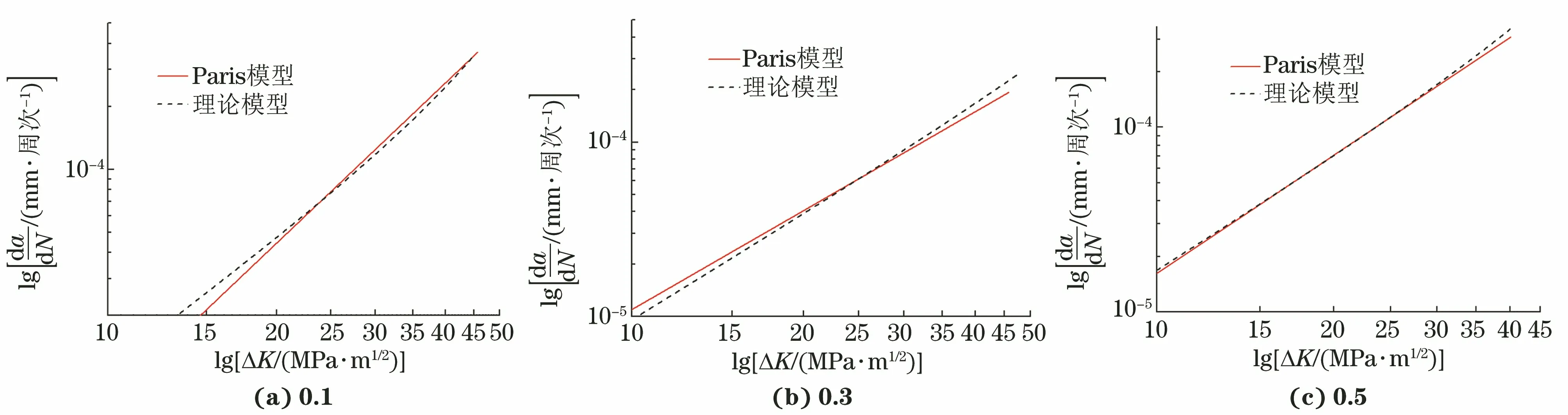
图7 不同应力比下理论模型计算得到E690高强钢在质量分数3.5% NaCl溶液中的腐蚀疲劳裂纹扩展速率与Paris模型计算结果的对比Fig.7 Comparison of corrosion fatigue crack growth rate of E690 high strength steel in 3.5wt% NaCl solution calculatedby theoretical model and Paris model at different stress ratio