基于沉降点占比的非错台型桥头沉降检测方法

张 萌，温 添，陆 键，郎 洪，陈圣迪

(1.同济大学 道路与交通工程教育部重点实验室，上海 201804; 2.上海海事大学 交通运输学院，上海 201306)

0 引言

我国江河湖泊众多，水系发达，桥梁成为连接渡水公路的主要技术手段，住建部最新统计数字显示，仅江浙沪三地城市桥梁总数就多达32 515座[1]。以宁波市为代表的江南地区地基以软土为主，修建在这类地基上的公路与桥梁在通车运营后多发生路桥连接处的差异沉降，产生桥头沉降现象，造成车辆经过时的颠簸，这会影响行车平顺性和车内人员的乘坐舒适度，严重时还会危及行车安全。

为及时掌握桥头沉降的发育演变规律，采取及时有效、经济性的处治措施，需要对其定量检测。目前描述桥头沉降的指标[2]主要有工后沉降量、沉降纵坡差、垂直错台高度、国际平整度指数IRI与标准偏差σ、车辆加权加速度均方根等，具体的检测方法有水准仪测量法、3米直尺法、连续平整度仪、车载式颠簸累积仪、多功能激光平整度检测仪测量法[3]和平整度惯性剖面仪测量法[4]等。其中，水准仪测量法通过测量路桥过渡段上布设测点的高程来绘制纵断面线，并对比竣工验收纵断面线测得工后沉降量；3米直尺法是将直尺置于路桥过渡段上，将楔块塞入尺底间隙并读取最大间隙值，以此来描述桥头沉降，上述两种方法检测效率和采样密度低且易受交通流和管制影响。考虑到桥头沉降会影响路面平整度，一些学者应用平整度类检测设备检测桥头沉降，但连续平整度仪、车载式颠簸累积仪、多功能激光平整度仪和平整度惯性剖面仪均仅能对短波长即路面的局部凸起和凹陷达到较好地检测效果，对于长波长即区段型沉降灵敏度较低，且利用上述设备检测桥头沉降时，连续平整度仪易受坑槽等路面病害干扰；车载式颠簸累积仪与车速密切相关，须考虑结果修正；多功能激光平整度仪和平整度惯性剖面仪虽检测精度高，但无法较好地反映桥头沉降的真实状况。此外，桥头沉降造成车辆颠簸和车上人员乘坐舒适性变化，我国GB/T 1344.1—2007机械振动与冲击标准[5]建立了车辆振动与乘坐舒适性的联系，一些学者便由此入手，通过检测车辆经过沉降处时的振动加速度变化[6-8]，或驾驶员的心率变化[9]间接表征了桥头沉降状况，但上述方法均通过研究车和人来间接量化桥头沉降状况，未测得直接反映桥头沉降的相关指标，这就无法为处治措施提供定量的决策参考，且车辆振动加速度、人体乘坐舒适性和心率变化皆与车速密切联系，难以获得标准化的检测结果。

2018年5月正式实施的我国《公路技术状况评定标准》[10](下称《标准》)新增路面跳车内容，《标准》规定使用断面类设备检测路面跳车，消除纵坡和异常值对路面高程的影响后，以0.1 m为采样间隔、10 m为统计单位计算单位长度内路面高程极差，结合计算结果与3等级路面跳车程度划分标准得到各单位路段内的跳车评价结果，再根据路面跳车扣分标准和相关计算公式得到路面跳车指数(PBI)。然而《标准》新增的路面跳车内容关注的主要是由路面局部凸起、凹陷及路桥异常连接引起的跳车，即仅包含错台型桥头沉降，尚未包含其他类型的桥头沉降，即由非错台型桥头沉降引发的跳车研究仍基本处于空白状态。

基于路面平整度测量的桥头沉降检测技术提供了一种代替主观、低效的人工测量的方法，然而，平整度设备对桥头沉降检测的适应性较差，且在此领域尚存在一定的技术缺陷；通过对车和人的研究间接量化桥头沉降状况是一种新的研究思路，但未还原道路自身的病害状况，且因车速影响须修正计算结果；《标准》规范了错台型桥头沉降的检测与计算，但尚未涉及非错台型桥头沉降。鉴于此，本研究针对《标准》未涉及的非错台型桥头沉降进行研究，提出利用车载式检测系统快速采集路桥纵坡与路面图像，形成道路纵断面线，并结合连续的路面图像在图线上定位路桥连接位置，基于此建立起桥头沉降计算模型和算法，形成了一种非错台型桥头沉降检测方法。最后，在宁波境内开展了多组试验与计算分析，并对比人工测量结果评估了该方法。

1 沉降类型与检测技术

1.1 桥头沉降类型

桥头沉降是由路桥连接处的不均匀沉降导致的，根据沉降后的道路线形特征可将其分为错台型、折线型和曲线型3类[11]，如图1所示。错台型沉降指因路桥差异沉降或路面材料剥落产生的路桥连接处“台阶”状沉降，如图1(a)所示；折线型沉降常发生于设有桥头搭板的路桥过渡段，显现出纵坡变化较为均匀的折线，如图1(b)所示；发生桥头沉降后的道路纵断面线呈现出曲线的特征，这种桥头沉降称为曲线型沉降，如图1(c)所示。

图1 3类桥头沉降Fig.1 Three types of bridgehead settlement

上述3类桥头沉降中，错台型桥头沉降呈现出局部凸起的特征，对于这类道路纵断面高程具有突变特征的沉降，《标准》的路面跳车内容已对其检测和计算作出了规定，而折线型和曲线型桥头沉降由于具有渐变性和区段性，不再适用于路面跳车相关内容，故这两类非错台型桥头沉降成为研究对象和重点。

1.2 检测技术

两类非错台型桥头沉降在道路线形上呈现出不同特征，故提出基于道路纵断面线研究桥头沉降的检测方法。对两类沉降的检测，利用断面类检测技术，同时搭载路面图像检测设备，形成车载式非错台型桥头沉降检测系统，如图2所示。车载式检测系统主要包含检测车、惯性导航系统、线扫描相机、光电编码器DMI、GPS、工业控制机和计算机显示器等。其中，惯性导航系统用于采集道路纵坡数据，光电编码器DMI用于获取实时车速与行驶距离，它们共同为计算获取道路纵断面线提供数据基础；线扫描相机作为路面图像检测设备可拍摄连续的路面图像，当实现道路纵断面线与路面图像位置对应后，即可在图线上快速定位路桥连接位置(桥接缝)。

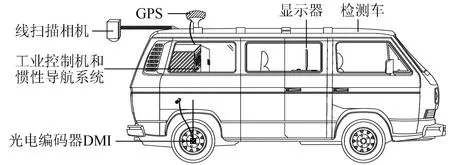
图2 车载式非错台型桥头沉降检测系统Fig.2 Vehicular non-staggered-step bridgehead settlement detection system

2 桥头沉降计算方法

2.1 数据预处理

车载式检测系统可获取检测车的行驶距离、车速、俯仰角(纵坡度)、横滚角(横坡度)、三轴(X/Y/Z)加速度等信息，利用纵坡数据和行驶距离，根据式(1)，(2)计算得各采集点相对出发点的高程(出发点高程记为0)，平滑连接行驶距离-高程二维点形成的图线即为道路纵断面线。

hi=(Li-Li-1)×sinθi-1,i=2,3,4,…,n,

(1)

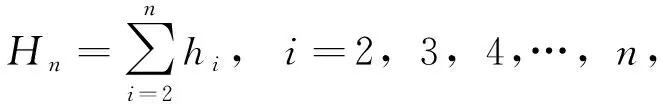
(2)

式中，hi为第i点较前一点的高程变化值；Hn为第n点相对出发点的高程；n为系统采集的点总数；Li，Li-1分别为第i，i-1点处检测车的累计行驶距离；θi-1为系统采集的第i-1点的俯仰角，上坡为正，下坡为负。

2.2 桥头沉降计算模型及算法

2.2.1 计算指标及阈值规定

现有研究成果中，描述桥头沉降状况的指标已有多类，主要包括路桥连接处错台高度[12-13]、路桥过渡段工后沉降量[14]、桥接缝前后纵坡差值[15]等。本研究利用桥接缝前后纵坡差值这一指标来量化桥头沉降状况，与上述研究不同的是，本研究“化线为点”，着重考察研究区段内均匀选取的各点前后纵坡差值，以超过纵坡差阈值的点占取点总数的比例来评价非错台型桥头沉降状况。上述超过纵坡差阈值的点称“沉降点”，其比例即本研究提出的计算指标，被定义为“沉降点占比”。

沉降点占比的计算基础是对纵坡差阈值的选取，由于以宁波为例开展桥头沉降研究，故根据宁波市城市管理局相关技术导则[16]对不同车速下相邻最大纵坡差的规定，同时考虑城市桥梁即城市道路的限速一般为80 km/h，提出了如表1所示的不同车速下的纵坡差阈值规定。

表1 不同车速下的纵坡差阈值规定Tab.1 Regulation of longitudinal slope difference thresholds at different vehicle speeds

2.2.2 模型及算法

由于桥头沉降主要发生于路桥连接处，故研究区段应为桥接缝前后的一段距离，对于不设桥接缝的对象，试验前应在路桥连接处进行标记，使得能在路面图像上清晰识别路桥连接位置。将道路纵断面线和路面图像位置对应后，基于图像在纵断面线上定位桥接缝，此时，纵断面线起点为采集开始点，重新设置桥接缝位置为纵断面线水平方向0点，如图3所示。

计算模型适用于上桥和下桥两处的桥头沉降，下面以上桥为例阐述计算模型。如图3(a)所示，在纵断面线上定位桥接缝位置点，由图线上的高程突变点定位过渡段起点，两点间的水平距离定义为l0，截取水平方向上-l0～l0范围内的纵断面线，并在图线上沿水平方向以Δl为间隔均匀取点；如图3(b)所示，沿水平方向对各点前、后l1(l1>Δl)距离拉坡，由于l1大于Δl，故图3(a)中所取点中仅部分点参与是否为沉降点的判定，将这部分点称为“有效计算点”，其数量定义为ne，各点序号为k。上述各参数取值规则将在下文试验与结果分析部分叙述。

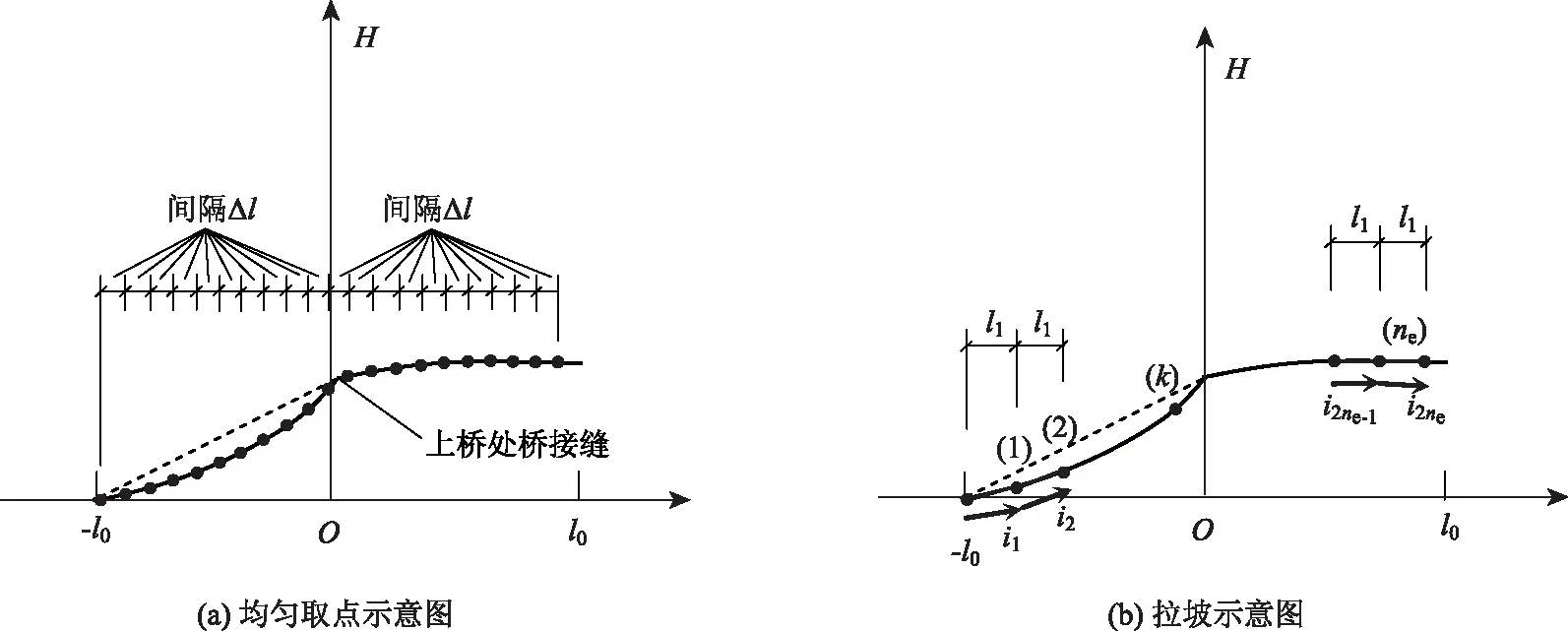
图3 桥头沉降计算模型示意图(单位：m)Fig.3 Schematic diagram of bridgehead settlement calculation model(unit：m)

非错台型桥头沉降计算模型如下：

(1)计算拉坡后各有效计算点前坡坡度i2k-1(%)和后坡坡度i2k(%)：

(3)

(4)

式中，Hk为第k个有效计算点的高程；Hk-1为第k-1个有效计算点即第k个有效计算点前坡起点的高程，H0记为0；Hk+1为第k+1个有效计算点即第k个有效计算点后坡终点的高程；Hne+1为纵断面线终点高程；其他符号同前。

(2)计算拉坡后各有效计算点前坡与后坡差的绝对值Δik(%)：

Δik=|i2k-i2k-1|,k=1,2,3,…,ne。

(5)

其中，有效计算点数ne按式(6)计算，结果取整：

(6)

(3)根据试验车速确定纵坡差阈值(表1)，记为i0，若某有效计算点前坡与后坡差的绝对值Δik超过该阈值，则判定该点为沉降点，nk记为1，反之记为0，即：

(7)

(4)计算沉降点数量N及其占有效计算点数ne的比例，即沉降点占比SPR(Settlement Points Ratio)：

(8)

(9)

上述计算模型形成了一种非错台型桥头沉降分析算法，其算法流程图如图4所示。基于此算法可编写相关计算机程序，实现对非错台型桥头沉降的自动和快速计算，计算结果可为路桥处治决策提供量化参考。

图4 桥头沉降检测算法流程图Fig.4 Flowchart of bridgehead settlement detection algorithm

3 试验与结果分析

3.1 道路纵坡自动化检测准确性验证

为保证车载式检测系统采集的道路纵坡结果在容许误差范围内，在正式试验前须先对其做纵坡自动化检测的准确性验证。在此之前已参照《公路路面技术状况自动化检测规程》[17]有关距离自动化测量的准确性验证要求进行了试验，试验结果符合《公路路面技术状况自动化检测规程》[17]和《多功能路况快速检测设备》[18]中距离自动化测量误差不超过0.1%的规定，即检测系统对车行距离的自动化检测符合要求。

选取一条长约150 m、纵坡变化显著的直线测试路段，在路段起终点位置做明显标记，并沿行车方向每10 m标记一个测点位置；利用DSZ05型水准仪沿行车方向逐一测量两相邻测点高程，根据式(10)计算两相邻测点间的纵坡值，将此结果作为两测点间的已知纵坡，见图5。此外，利用车载式检测系统分别以20，30和40 km/h匀速检测测试路段，系统按0.1 m间距采集纵坡数据并以10 m为单位输出平均纵坡，作为纵坡自动化测量结果。

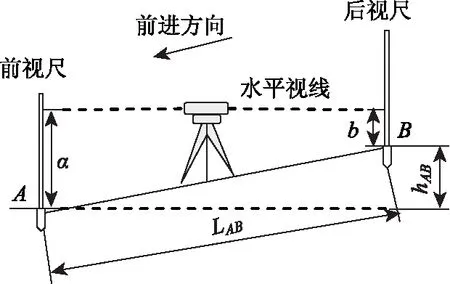
图5 纵坡自动化检测准确性验证人工试验Fig.5 Manual test for verifying accuracy of longitudinal slope automatic detection

(10)

式中，IHM为人工测量的两相邻测点间纵坡值；hAB为水准仪测量的两相邻测点间高差；LAB为两相邻测点间距离，此处取10 m。

对测量结果进行误差分析，选取绝对误差(Absolute Error)和相对误差(Relative Error)作为纵坡自动化测量的准确性验证参数，其计算公式如下：

(11)

式中，EAE为两相邻测点间纵坡测量的绝对误差；ERE为两相邻测点间纵坡测量的相对误差；IAM为车载式检测系统以10 m为单位输出的两相邻测点间的平均纵坡值。

分析结果见表2，自动化和人工测量的纵坡结果共15组，分别按0～10，10～20,…，140～150 m 即10 m为单位分布。由表可知，3种车速下的15组纵坡测量结果绝对误差EAE均小于6%，即同一车速下的所有检测值绝对误差小于6%。同时，20 km/h车速下0～10，10～20和140～150 m距离范围内的相对误差ERE分别为13.25%，10.39%和10.25%，均大于10%，使此车速下有80%的检测值相对误差小于10%；30 km/h和40 km/h车速下相对误差小于10%的检测值占比分别为86.67%和100%。20 km/h和30 km/h车速下满足相对误差要求的检测值比例虽不足95%，但100%检测值的绝对误差小于1.5%，即绝对误差小于1.5%的检测值比例大于95%。综上所述，上述3种车速下的误差分析结果均符合我国JTG/T E61—2014标准规范中的相关规定，证明本研究采用的车载式检测系统满足纵坡自动化检测的准确性要求。

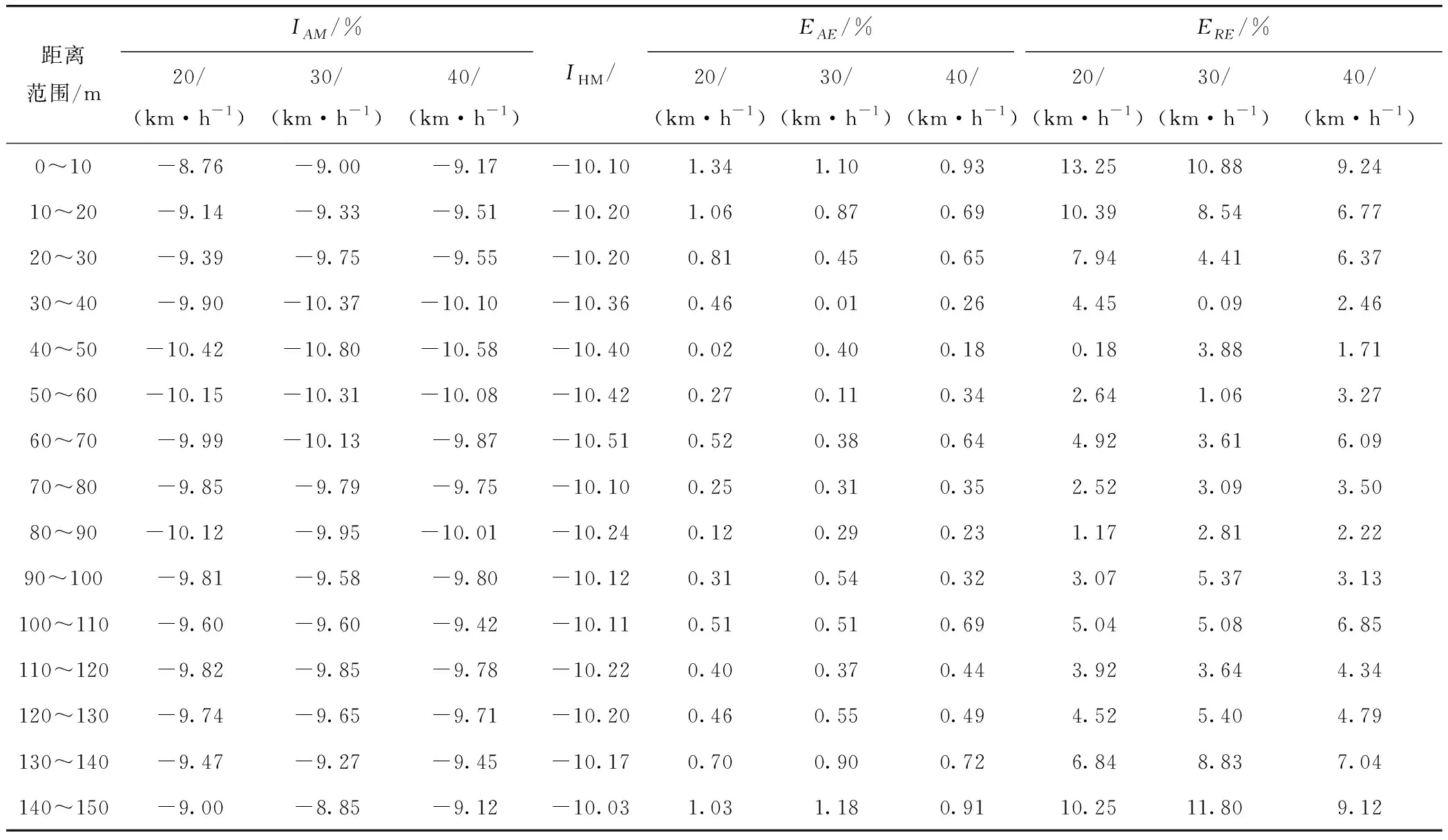
表2 车载式检测系统与人工测量结果误差分析Tab.2 Error analysis between vehicular detection system and manual measurement result

3.2 桥头沉降相关性分析

3.2.1 自动化与人工试验方案

如图6所示，搭载检测系统的检测车经加速后匀速通过路桥过渡段和桥梁段，采集数据与图像，完成后经减速停车。考虑行车安全，并减小车辆颠簸对试验结果的影响，检测车加速后以不大于40 km/h的车速匀速行驶。基于构建的桥头沉降计算模型和算法，输入检测系统采集的数据和图像，即得到各试验对象的沉降点占比SPR。

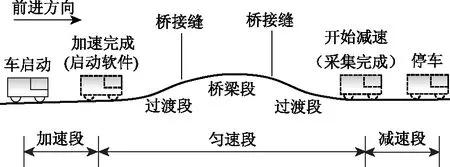
图6 车载式检测系统采集道路纵坡及路面图像Fig.6 Collecting road longitudinal slope and pavement images by vehicular detection system

同时，考虑到桥头沉降由路桥间的不均匀沉降产生，通过测量两者的纵坡差值来描述桥头沉降状况。如图7所示，利用水准仪测量桥接缝处、桥接缝前l0距离处、桥接缝后l0距离处3点高程，通过式(12)计算过渡段和桥梁段纵坡值及两者差的绝对值。

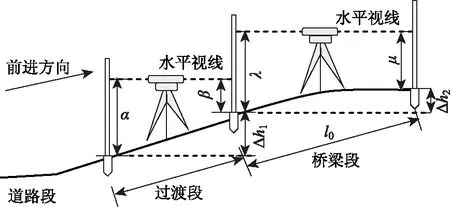
图7 人工测量道路纵坡Fig.7 Manual measuring road longitudinal slope

(12)

式中，l0为人工测量纵坡选取的桥接缝桥前(后)距离，意义同上文计算模型中相同参数；Δh1，Δh2分别为桥接缝前、后l0距离内过渡段、桥梁段高差；I1，I2分别为桥接缝前、后l0距离内人工测量的纵坡值；ΔI为人工测量的桥接缝前后纵坡差绝对值。

3.2.2 结果相关性分析

在实际情况下，错台型桥头沉降常发生在路桥平直连接(无显著纵坡变化)和桥接缝路面材料显著剥落的桥头处，而这里研究的是非错台型桥头沉降，为使提出的检测方法适用对象正确，选取上下桥纵坡变化显著且桥接缝处无明显材料剥落的桥梁为试验对象。

对于模型参数的取值，考虑了《标准》[11]对路面跳车检测采样间隔为0.1 m的规定和实际应用模型时取点密度对计算结果的影响，同时考虑了《导则》对检测车轴距的规定及实际应用模型时拉坡长度对计算结果的影响，综上所述，按如下规则对模型参数进行取值：

(1)对于模型中的l0：精确到0.05 m，根据试验对象的纵断面线不同，其取值不同。

(2)对于模型中的Δl：当l0>5.0 m时，Δl取0.5 m，反之，Δl取0.1 m。

(3)对于模型中的l1：当l0>5.0 m时，l1取2.0 m，反之，l1取1.0 m；

(4)对于模型中的i0：由于各组试验的检测车速均小于40 km/h，按表1规定，i0取4%。

按上述试验方案、试验对象和参数取值原则选取了浙江宁波境内的100座桥梁，利用车载式检测系统采集其纵坡数据和连续路面图像，并通过所建立的计算模型与算法获得了200组(上、下桥)沉降点占比SPR。同时，按人工试验方案在各试验对象的上、下桥处测得过渡段与桥梁段纵坡差绝对值ΔI，产生200组人工试验结果，部分结果如表3所示。

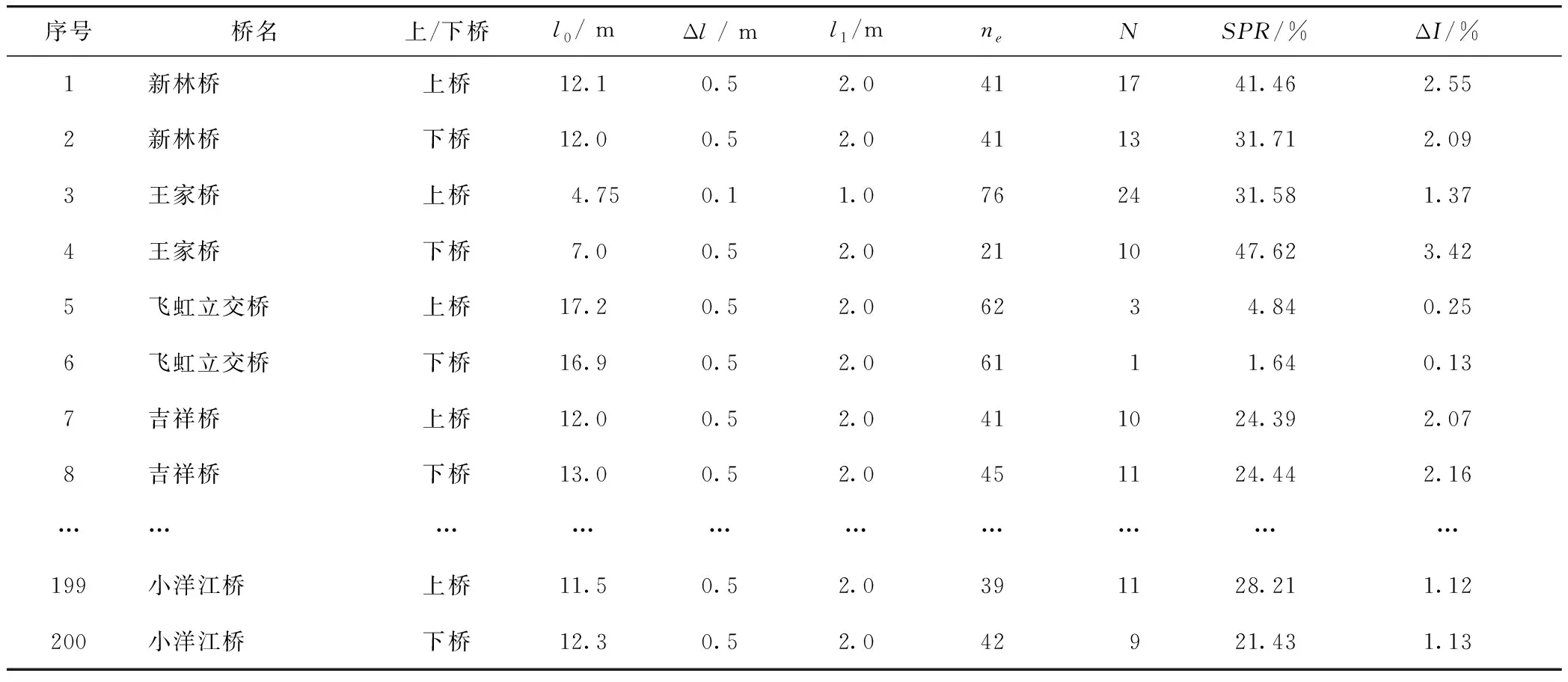
表3 自动化与人工试验结果Tab.3 Result of automatic and manual test

为进一步分析计算模型及算法的输出结果和人工测量结果的相关性，将上述200组沉降点占比SPR与人工测量的纵坡差绝对值ΔI做相关性分析，得到两者的相关系数r=0.957 4，p值为0，说明两者显著相关。进一步利用Origin软件建立两者间的线性回归模型，模型拟合结果如图8所示。分析得，SPR和人工测量结果的决定系数为0.916 6，表明所建立的回归模型具有较高的拟合精度，进而验证了所提出的非错台型桥头沉降检测方法及模型参数取值规则是科学合理的。

图8 模型及算法结果与人工测量结果的线性回归模型Fig.8 Model of linear regression between results of model +algorithm and manual measurement

4 结论

(1)对于非错台型桥头沉降，现行国家标准未对其检测方法作出规定，且现有方法效率低、主观性强、对区段型沉降灵敏度低、易受变形类病害干扰等，针对上述问题，提出利用车载式检测系统快速采集路桥纵坡与路面图像数据，形成与图像位置对应的道路纵断面线，并基于此建立了非错台型桥头沉降计算模型与算法，其中提出了一项计算指标即沉降点占比SPR。

(2)对车载式检测系统自动化检测道路纵坡的准确性进行了试验验证，结果表明，3种车速下各15组距离梯度的道路纵坡自动化检测结果与人工测量结果的误差均符合有关标准规范的规定，即检测系统满足纵坡自动化检测的误差要求。

(3)规定了试验对象选取和模型参数取值规则，在浙江宁波境内对100座桥开展了自动化和人工试验，对自动化检测数据利用所建模型与算法输出了200组(上、下桥)SPR，并将其与人工测量的200组纵坡差绝对值ΔI进行了相关性和回归分析。结果表明：两者的相关系数为0.957 4，p值为0，回归模型决定系数为0.916 6，两者显著相关，说明提出的检测方法和参数取值规则是科学合理的，能够准确定量描述非错台型桥头沉降状况。

(4)所提检测方法填补了桥头沉降检测的研究空白，对于自动化定量检测其沉降状况具有重要的应用价值，但此方法为单车道逐一检测，针对一次性检测多车道下的桥头沉降状况还需深入研究，且未来需添加全国其他地区的数据集，进一步优化所提检测方法，从而增强模型的普适性。