基于MOPSO算法的商用车气制动系统优化

郭冬妮，李孟华，阎阔，李法兵，郑鑫，张军

1.一汽解放集团股份有限公司，吉林长春 130011；2.陆军装备部驻沈阳地区军事代表局驻长春地区第二军事代表室，吉林长春 130011；3.蒂森克虏伯富奥汽车转向柱(长春)有限公司,吉林长春 130011

0 引言

在车辆安全性越来越受重视的今天，设计出既能满足用户需求，又兼顾经济性的制动系统成为汽车工程师的重要目标。现有的针对制动系统的优化一般只针对性能提升单方面的研究，缺少统筹兼顾性能及成本的多目标优化。本文通过采用具有快速收敛特性的多目标粒子群方法作为优化算法，根据影响制动系统性能和成本的12个优化变量构建了基于响应时间和系统成本的双目标函数，利用MATLAB-AMESim联合仿真平台对其进行了优化设计，确定了一种兼顾性能和成本的气制动系统优化方案，为产品性能改进指明方向。

1 粒子群优化算法介绍

粒子群优化算法(particle swarm optimization,PSO)是一种基于生物种群模型的原理简单、收敛迅速的优化算法。其基本原理是对鸟群飞行和觅食过程中的飞行行为的仿生模拟。粒子群优化算法的原理如图1所示。

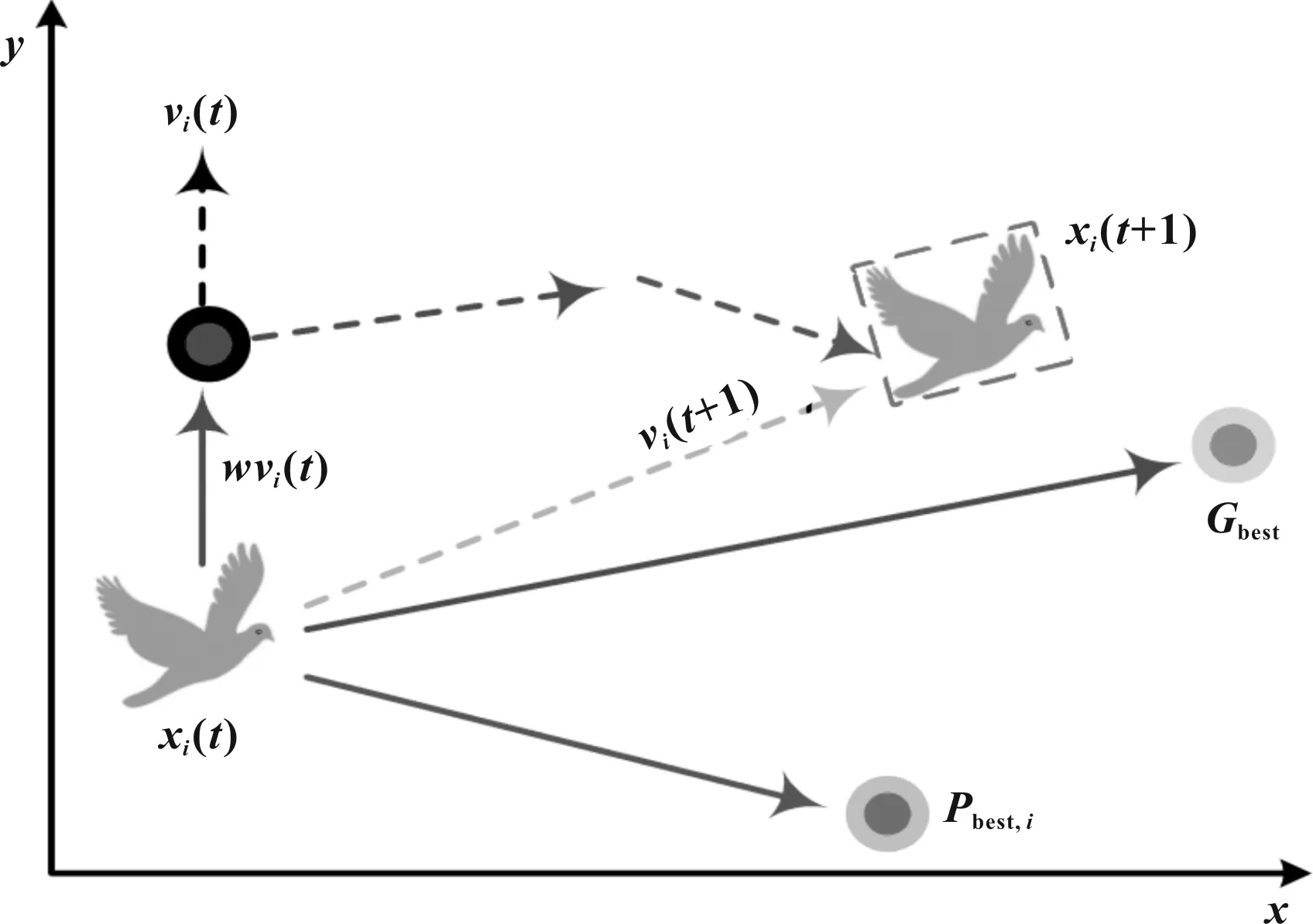
图1 粒子群优化算法的原理

在PSO算法中，粒子表示单个飞鸟，粒子的全集合表示鸟群。根据鸟群飞行原理，每个粒子分配速度和位置两个属性参数。每个粒子都能判断出整个群体中的最优位置和当前飞行轨迹中的最优位置。通过对鸟群历史最优位置和当前最优位置的判断，粒子经计算可以得出下次飞行的速度和方向，不断循环这个过程，整个鸟群将实现快速收敛至最优解集。

1.1 粒子群优化算法基本流程

基于粒子群优化算法原理，粒子群优化过程可以划分为粒子初始化、最优单体选择、粒子速度和位置更新、外部档案更新以及最优解判定等几个过程，PSO基本流程如图2所示。在初始化过程中，首先对所有粒子进行随机赋值，以实现算法的运行；进而在最优单体选择环节，根据目标函数的计算方法对每个个体的历史最优解以及所有个体的全局最优解进行选择和记录；然后根据最优个体的情况，依据粒子速度和位置的更新方程对粒子进行更新。对于档案更新环节，算法的每次迭代都会以档案内现有解和待进入解之间的支配关系来更新外部档案。对进入解与现有解进行比较，将被支配的新解或现有解舍弃删除一些相对较差的解以释放空间，确保新解能够存入档案。

图2 PSO基本流程

1.2 粒子速度与位置更新

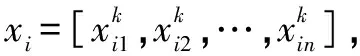
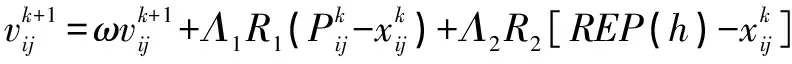
(1)

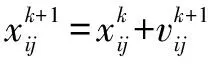
(2)

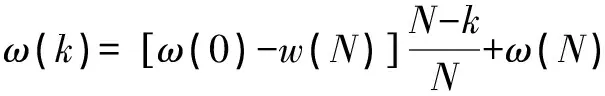
(3)

其中为惯性权值，其值越大，粒子速度越快，全局最优解的搜索能力越大，粒子对新信息的接收度越差，局部搜索能力越差。和分别为学习因子，的值越大，粒子越依赖自身的经验，且越趋于稳定运行；的值越大，粒子越依赖社会经验，且越趋于灵活运行；和在0～1之间随机取值。为由非支配解构成的外部档案集；()为通过自适应网格法从里选取的值。

2 多目标优化函数构建

2.1 目标函数构建

文中的目标是在优化制动响应时间的同时尽可能节约成本,因此多目标优化问题可以表达为：

Minimize={(),()}

(4)

式中：为由制动系统响应时间关键影响因素构成的矩阵;为制动系统响应时间;为制动系统成本。

矩阵共有12个变量，分别为：制动阀上腔进气管直径、制动阀下腔进气管直径、制动阀上腔出气管直径、制动阀下腔出气管直径、上腔排气间隙、下腔活塞直径；继动阀进气管直径、继动阀进气管2直径；前桥ABS电磁阀进气管直径、后桥ABS电磁阀进气管直径；前桥制动气室进气管直径、中后桥制动气室进气管直径。

成本依照活塞直径及管路直径大小进行线性计算，活塞直径及管路直径越大，成本就越高，根据实际供应商价格数据，设定管路直径每增加1 mm，每米成本增加10元，活塞直径每增加1 mm，成本增加20元；制动阀上腔排气间隙的成本定为0元。文中以6X4载货车为研究对象，其制动阀上腔进气管、下腔进气管、上腔出气管、下腔出气管、继动阀进气管、继动阀进气管2；前桥ABS电磁阀进气管、后桥ABS电磁阀进气管；前制动气室进气管、中后桥制动气室进气管的长度分别为4 680、4 870、6 830、1 800、3 030、2 300、7 250、1 160、4 165、1 700 mm，最后得出成本计算公式为：

=468×+487×+683×+18×+303×+

23×+725×+116×+4165×+17×+20×

(5)

2.2 约束条件确定

根据主机厂实际可采购的气管类型，管路直径的取值范围为3～12 mm，活塞直径的取值范围为60～100 mm。

2.3 参数选择

2.3.1 种群规模

种群规模的设定需考虑模型的复杂度、目标的个数以及对优化程度的需求。文中设定种群规模为30。

2.3.2 学习因子

在初始飞行阶段，种群未获得足够的信息，社会经验参考价值不高，此时应增大；随着飞行不断进行，粒子信息充足，社会经验有较高参考价值，此时应增大。和的计算公式如下：

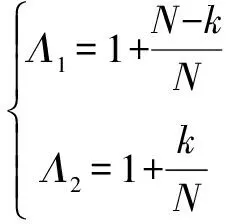
(6)

式中：是最大迭代次数，取值为100。

3 基于MATLAB-AMESim联合仿真的优化算法实现

3.1 优化算法实现步骤

在气制动系统优化问题中，粒子的位置代表了各参数下的制动响应时间，算法实现步骤如下：

(1)初始化。对种群中所有粒子的位置和速度在定义域内进行随机赋值。

(2)通过联合仿真对各粒子位置进行仿真计算，并得到各粒子的适应度值。

(3)根据各粒子适应度值，求解非支配解集，同时更新外部档案。

(4)根据公式(4)更新粒子速度。

(5)根据公式(5)更新粒子速度。

(6)判断是否达到终止条件。

(7)如果未达到终止条件则重复步骤(2)～(6)的过程，直到达到终止条件。

3.2 优化结果分析

按照GB 12676—2014的规定，制动系统响应时间必须在0.6 s以内，根据要求舍弃结果中响应时间大于0.6 s的解，得出最优解如图3所示。

图3 最优解

由图3可以看出，Pareto解集是散点，说明制动系统响应时间和系统成本相互矛盾，不能同时最优。此次优化共有最优解15个。由图3还可以看出，制动响应时间和成本不能同时取得最优解，其中点为制动系统响应时间最优解，系统响应时间为0.44 s，系统成本为399.3元；点为成本最优解，系统响应时间为0.59 s，系统成本为327.2元。

图4列举了其中两个粒子的飞行轨迹，其中上腔出气管直径的轨迹为由大变小，最终收敛至最小值，这说明随着上腔出气管直径的变化，制动系统响应时间和系统成本变化趋势相同;下腔出气管直径粒子的轨迹是不断波动不收敛状态，说明随着下腔出气管直径的变化，制动系统响应时间和系统成本变化趋势矛盾，导致粒子轨迹无法收敛。

图4 粒子飞行轨迹示例

设置制动系统响应时间和系统成本两个要素的权重均为50%，将要素分别进行归一化，可得气制动系统优化的目标函数:

=05+05

(7)

其中是归一化后的制动系统响应时间，其值越小越好；是归一化后的系统成本，其值同样是越小越好；所以函数的最小值就是本次优化的最优解。

取最优解时，制动系统响应时间是0.47 s，系统成本是367.2元。最优解具体数值如下：制动阀上腔进气管直径=10 mm、制动阀下腔进气管直径=10 mm、制动阀上腔出气管直径=4 mm、下腔出气管路直径=9mm、继动阀进气管直径=9 mm、前桥ABS电磁阀进气管直径=8 mm、后桥ABS电磁阀进气管直径=7 mm、前桥制动气室进气管直径=10 mm、中后桥制动气室进气管直径=7 mm、继动阀进气管2直径=11 mm、制动阀下腔活塞直径=77 mm。

将最优解的参数与原始制动系统参数所得制动系统响应时间曲线对比，结果如图5所示。

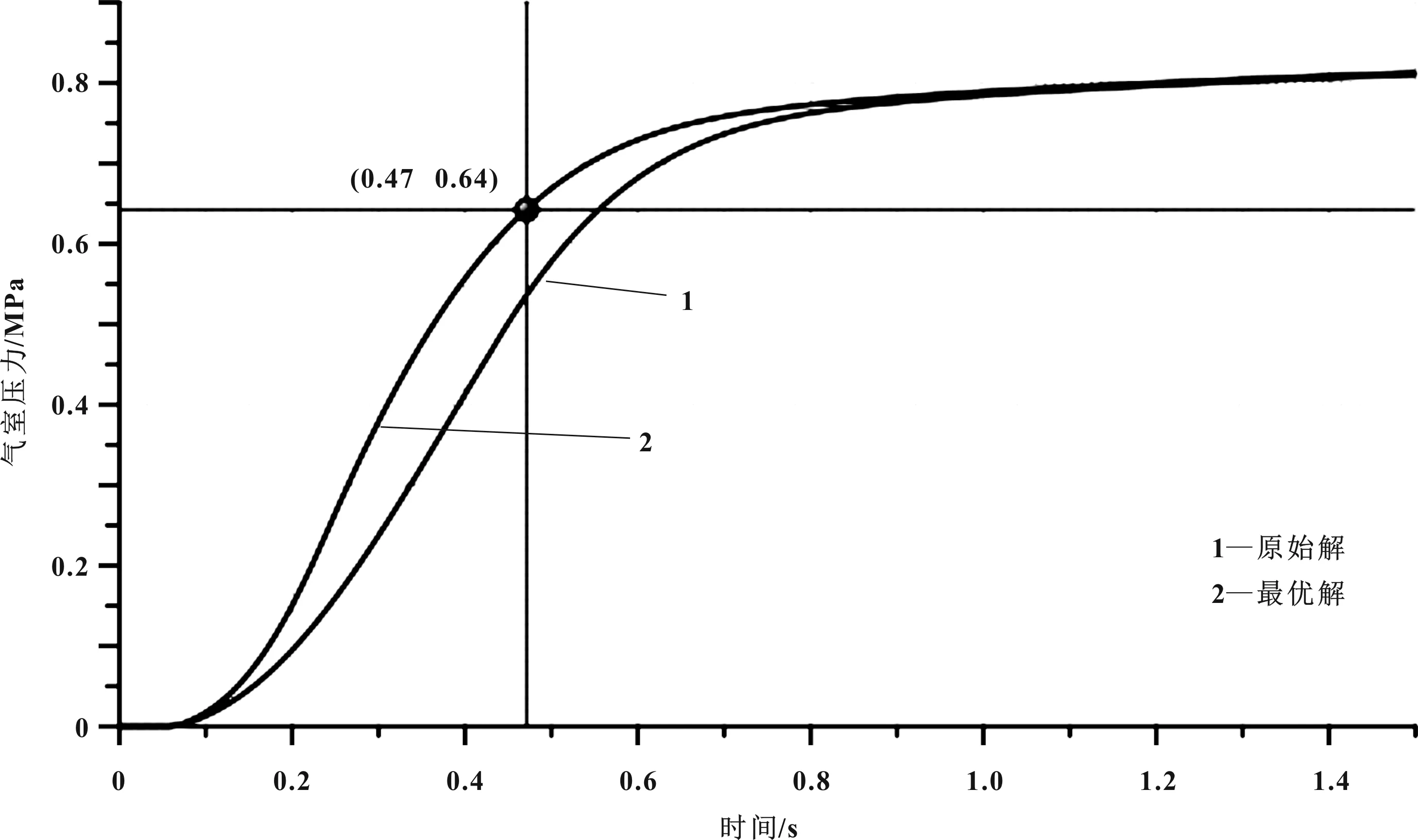
图5 制动系统响应时间优化前后对比结果

由图5可以看出，原参数制动系统响应时间是0.55 s，成本是427元；优化后响应时间是0.47 s，成本是367.2元。通过多目标粒子群优化算法，在系统成本降低14%的同时，响应时间加快了14.5%。

4 结束语

本文通过采用具有快速收敛特性的多目标粒子群方法作为优化算法，构建了基于响应时间和系统成本的双目标函数，同时根据市场供货能力和企业产品系列化需求，确定了各变量的约束条件，并完成了种群规模、学习因子、惯性权值等参数的选择；在此基础上，利用MATLAB-AMESim联合仿真平台对其进行了优化设计，以取得综合性能与成本的最优值，为新产品的开发和现生产车型的方案优化提供技术支持，缩短设计时间、节约开发成本，具有一定的理论意义和应用参考价值。