基于TRIZ理论的减振器流-固耦合特性仿真
2022-08-03张娜于振环杨坤刘志远
张娜,于振环,杨坤,刘志远
1.长春汽车工业高等专科学校机械工程学院,吉林长春 130011;2.长春汽车工业高等专科学校汽车工程学院,吉林长春 130011;3.一汽东机工减振器有限公司试验中心,吉林长春 130013;4.哈尔滨工业大学控制科学与工程系,黑龙江哈尔滨 150080
0 引言
车辆减振器是汽车悬架极其重要的部分,车辆行驶的操控稳定性能的好坏直接受其影响。电磁阀半主动减振器,又称为连续可变阻尼悬架控制系统,减振器的阻尼受电磁阀连续调节,以便适应复杂的路况,保持良好的操稳性。我国半主动悬架控制系统目前已经取得了很多成果,但是在使用中还存在一些不足。因此,本文基于TRIZ理论的新型创新原理给出了一种减振器,提升了半主动减振器的阻尼力值范围,利用创新理论深入开展车辆减振器的改进研究具有重要的理论和实际意义。
1 TRIZ理论新型创新原理表
创新是发明在某企业进行商品化的开发,企业通过产品在市场中获得了收益。找到系统当前的问题所在,通过创新方法将其达到理性状态的过程,就是解决问题的实质。文中主要应用TRIZ创新理论中Matrix 2003的创新原理表以及所对应的40个创新原理。MANN于2003年提出新型矛盾矩阵Matrix 2003。利用该矩阵可以推导出出现频率较高的创新法则,并将该法则应用到实际工程领域中,大大提高解决问题的效率。
在利用TRIZ理论新型创新原理表解决电磁阀半主动减振器的问题时,首先根据电磁阀半主动减振器遇到的具体工程问题,确定其有待改善的性能;然后将预改善的问题转化为TRIZ理论新型创新原理表的标准解,通过Matrix 2003表格,整理出出现频率较高的发明原理序号;最后将发明创新原理应用到具体的系统中,找出满足要求的有效解。
2 基于TRIZ理论的电磁阀减振器的分析
2.1 基于TRIZ理论嵌套原理的应用
电磁阀半主动减振器受自身机械结构限制,可调阻尼力范围小,如图1所示为电磁阀半主动减振器阻尼力曲线。有限的阻尼力范围严重限制了半主动悬架控制器的工作边界,影响了车辆的操稳性,所以势必要提高电磁阀半主动减振器阻尼力的范围。
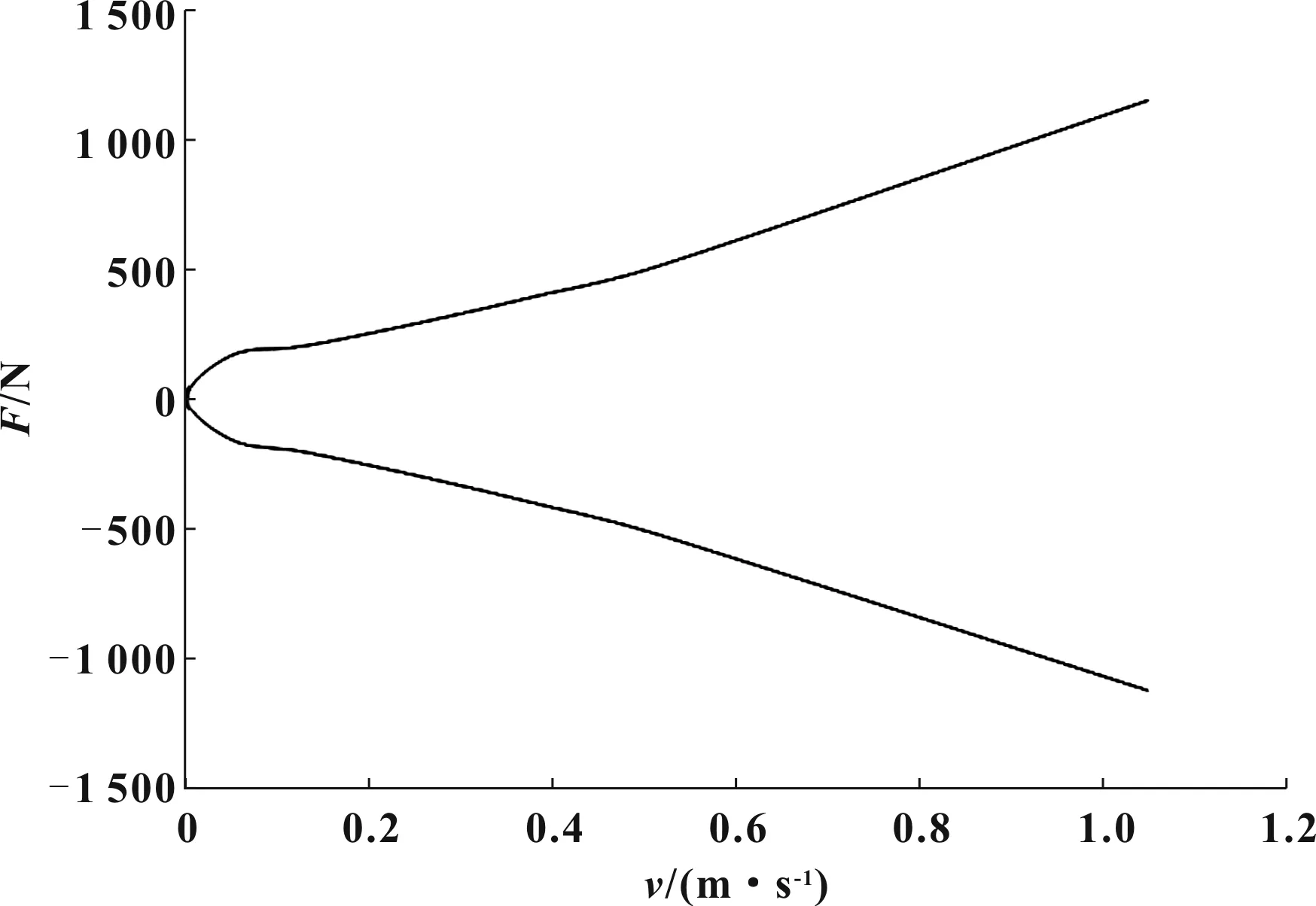
图1 电磁阀半主动减振器阻尼力曲线
为了解决以上问题,文中提出欲改善的工程特性为:应力或压力以及可靠性。
欲改善的工程特性对应的创新原理(一)见表1。由表可知,两个欲改善的性能中,同时包含的创新原理适用序列为NO.35、NO.10、NO.3和NO.4,TRIZ创新原理及其具体内容(一)见表2。
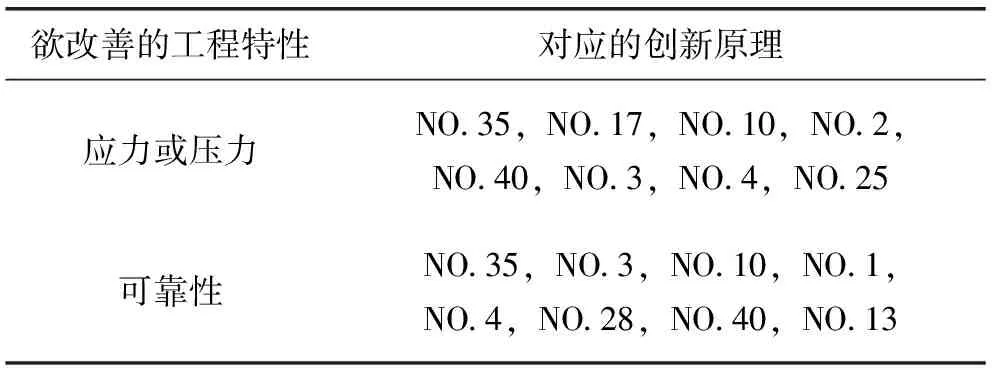
表1 欲改善的工程特性对应的创新原理(一)

表2 TRIZ创新原理及其具体内容(一)
嵌套原理的应用设想:改变系统的物理状态。液压油为电磁阀半主动减振器的主要成分,随着温度的变化,液压油的黏度系数也有较大变化,若黏度系数变化大,通过小孔的油液受到的阻力也变化,影响车辆行驶的稳定性,即该减振器可调阻尼力范围小。磁流变液(magnetorheological fluid,MR)属流动性可控的新型流体,是一种应用性较广的智能材料。外部无磁场时,MR流体呈现低黏度物理特性;外加磁场时,转化为高黏度、低流动性的物理特性。磁流变液具有转换能耗低、易于控制以及响应迅速等特点,在毫秒级时间内从任意流动的液体突变为半固体或者固体,可控流变特性即可显现出来。所以,根据嵌套理论的设想,将电磁阀半主动减振器内部的油液改为磁流变液,即可改善所需工程特性。
2.2 基于TRIZ理论机械替代及分离原理的应用
将电磁阀半主动减振器内部油液改为磁流变液又会遇到新的问题:磁流变液是由微小易磁化的颗粒分布于特定溶液中形成的特殊悬浮液体,由于磁流变液颗粒大且黏度系数较大,将其置于阀系结构复杂的电磁阀半主动减振器内部,会导致阀系机械结构严重损伤并失效。
为了解决以上问题,文中提出欲改善的工程特性为:物质损失和系统的复杂性。
由表3可知,两个欲改善的性能中,同时包含的创新原理适用序列为NO.28、NO.2、NO.10和NO.35,TRIZ创新原理及其具体内容(二)见表4。

表3 欲改善的工程特性对应的创新原理(二)

表4 TRIZ创新原理及其具体内容(二)
机械系统替代原理和分离原理的应用设想:将电磁阀半主动减振器中的“干扰”部分——阀系分离出去,再设计一套新的机械系统进行替代,如图2所示。
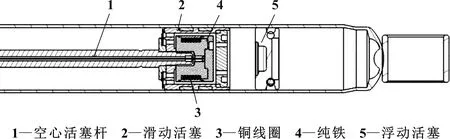
图2 新型减振器阀系结构
此新型减振器内部为磁流变液流动液体,液体黏度系数可随磁场强弱变化而变化,当磁场增加时,其黏度系数增加,液体流过活塞的节流孔后,减振器的阻尼力值也随之增加。在磁场作用下,磁流变液的流动黏度系数远大于电磁阀半主动减振器油液系数,产生的阻尼力值比电磁阀半主动减振器阻尼力值范围更大,能够增加控制器对作动器的控制范围,扩大控制算法数学模型的边界范围,能够提高车辆的操控稳定性。
3 新型减振器的有限元分析方法
3.1 流固耦合有限元数学模型
固体与流体之间的运动状态,可以利用流固耦合有限元分析方法来解决,它需要同时满足:流体耦合边界的动力学方程和运动学方程。固体耦合边界的运动学方程为
=
(1)
动力学条件为
=
(2)
式中:为流体边界位移;为固体边界位移;为单位外法线矢量;为流体应力;为固体应力。
利用运动学的条件,即可推导出以下条件
=
(3)
式中:为流体速度;为固体速度。
3.2 基于Adina的减振器阀系流固耦合有限元分析
利用流固耦合有限元对新型减振器阀系核心区域进行仿真分析时,有3个关键性问题需要解决:
(1)流固耦合面上的相互作用力需准确传递。Adina软件在仿真前需要分别建立固体与流体模型,并且在求解流-固耦合问题时要分别定义两个模型的耦合面上的边界条件。还要达到一定容差,设置的网格可以不完全一致。因此,为了确保在流固耦合面上准确传递作用力,在对MRD核心区域进行分析时,需采用如下处理方式:将处于流固耦合面上的流体节点位移与附近固体节点位移做插值,固体节点力通过对周围流体应力积分求得,即
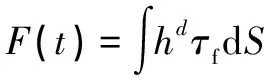
(4)
式中:为固体虚位移。
(2)固体变形引起流体网格移动的问题解决。这一问题的解决可以把欧拉方程导入ALE(arbitrary lagrangian euleria)。Adina软件中的流固耦合边界上,流体节点的位移以及速度取决于固体变形的程度,可通过对Laplace方程求解得到流体体积的变化量。与此同时,定义Leader-Follower点时,流体边界的网格可人为控制。
(3)高效求解耦合系统。直接法和迭代法是Adina的两种有效解法,进行动态分析时,流体和固体模型的积分点要求一致。为了对流-固模型分别求解,由于该模型的非线性特点,需要均采用迭代求解法。将流-固模型放在同一矩阵中求解,即直接解法,有限元方程为:
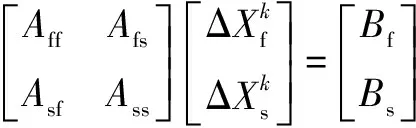
(5)
+1=+Δ
(6)
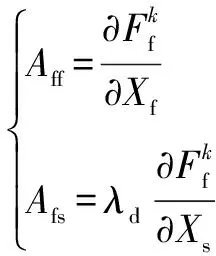
(7)
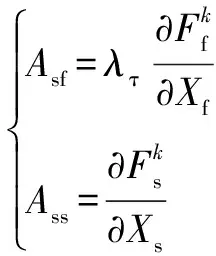
(8)
式中:为位移松弛因子,0<≤1;为应力松弛因子,0<≤1。
直接解法精确度很高,主要应用于计算量较小的非接触瞬态模型。
4 阀系核心区域流固耦合有限元分析
所述新型减振器的-特性曲线来自于其工作核心区域,必须分别建立流场模型和固体模型,可刚体处理工作缸。为求得最大减振器阻尼力-范围,所以只建立磁场最大模式下的阻尼力-范围,即最大磁场状态下的模型和求解结果。
4.1 建立三维流场有限元模型
图3为流场有限元模型,文中建立1/4有限元模型,为减少计算时间,在满足有限元计算精度要求前提下,单位体积的有限单元设置较大。由于流场运动剧烈,减振器的核心工作区域——活塞节流孔,有限单元需要较小的单位体积。流-固耦合面上的网格均可以通过Adina软件耦合计算,计算的收敛性即可提高。

图3 流场有限元模型
4.2 建立三维固体有限元模型
如图4所示,该模型包括活塞节流孔和活塞杆。文中建立1/4阀体模型,为保证流固耦合面密度相容性,单元划分采用八节点六面体。

图4 固体有限元模型
4.3 初始条件及边界条件
利用隐式动态法进行固体分析。如图5所示,为确保仿真流场与真实环境的一致性,将100 mm振幅的正弦波载荷加于活塞杆,软件中出口处压力值默认为零。
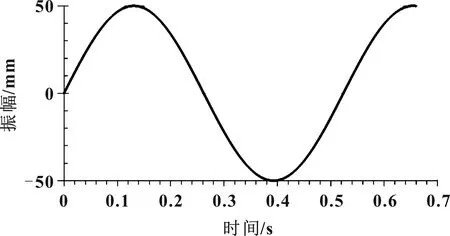
图5 加载正弦波
5 减振器仿真分析
5.1 减振核心区域的流场分析
核心区域的流场对减振器的特性有至关重要的影响,这一部分的流场变化剧烈。
图6为减振器压力云图。
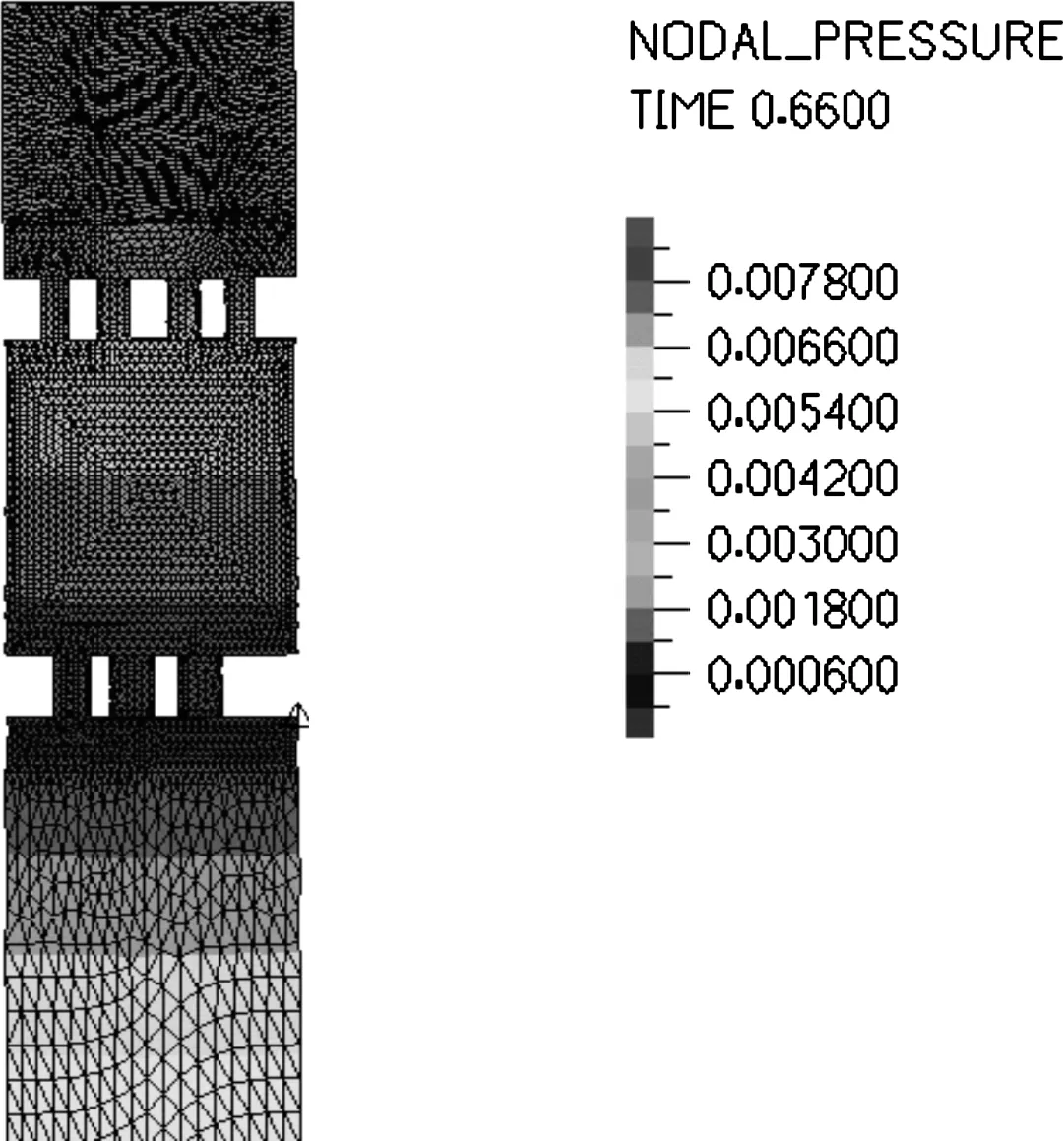
图6 减振器压力云图
由图6可以看出,减振器在工作状态下,活塞节流孔处压力集中。由图还可以看出,活塞节流孔明显具有节流作用,流场压力梯度分布明显,说明仿真的有效性。
图7为减振器流场速度流线图。由图可以看出,在节流孔处速度颗粒表现活跃,再次说明仿真具有真实性。
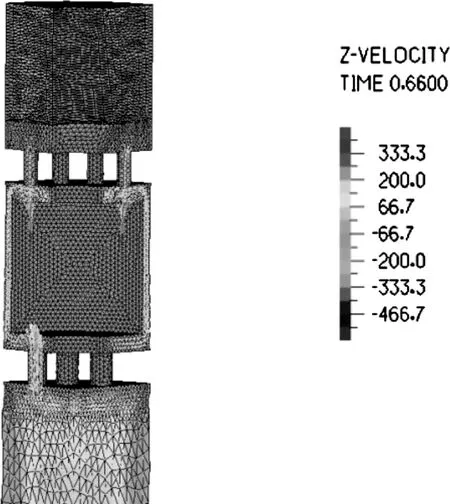
图7 减振器流场速度流线图
5.2 核心区域活塞节流孔特性分析
图8为减振器活塞应力云图。由图可以看出,活塞孔处及活塞本体受到的应力变大,同时流场区域的压力也在上升,使得活塞壁面受高速流体冲击,造成湍流流动。

图8 减振器活塞应力云图
5.3 减振器阻尼特性F-v对比
减振器阻尼力可调范围是减振器特性的关键问题之一,本文仿真磁场最大时的阻尼力-特性曲线。图9为减振器-特性曲线。由图可以看出,其阻尼力比电磁阀半主动减振器范围大,更有利于控制器对边界条件的控制。
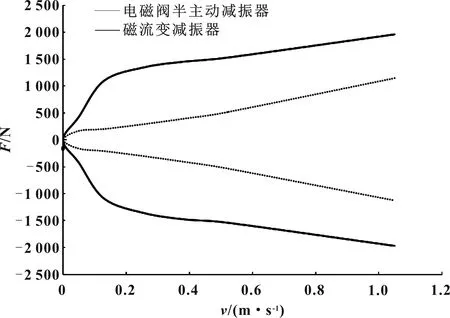
图9 减振器F-v特性曲线
6 结束语
本文通过TRIZ理论的新型原理表和创新原理对电磁阀半主动减振器的阻尼力特性进行全面分析,将其内部的油液和阀系进行改进,得出一种新型磁流变液减振器。并利用流固耦合有限元分析的方法,建立固体和流体三维有限元模型,得到固体和流体的应力和压力云图以及新型减振器最大阻尼力-特性曲线,并与电磁阀半主动减振器比较,阻力值范围明显增大。阻尼力可调节范围外包络曲线的增大,对车辆半主动悬架控制有极其重要的意义。文中的研究结果满足了TRIZ创新理论对理想解的要求。
