巧用计数器，让竖式除法教学厚重起来——以“除数是一位数的笔算除法”一课为例

黄兴发

(广德市实验小学教育集团西校区 安徽宣城 242200)

竖式除法学习对二三年级的小学生来说是一个挑战，因为竖式除法表达方式有些“怪异”，颠覆了学生对所学的加、减、乘竖式计算的固有认识，学生理解起来有一定的思维难度。为了突破这一难点，教师习惯采用分小棒的方法，直观形象，效果不错。但笔者认为，除法的计算过程就是数位的转换和数位上数值的分与合的过程，而使用计数器能够合理表达除法的运算过程，使运算过程更加直观。故笔在“除数是一位数的笔算除法”一课的教学中引入计数器，收到了很好的教学效果。接下来，笔者根据课堂教学实践谈一些粗浅的认识。

一、以计数器明算理，通算法

究其实质，除法是一个平均分的过程，就是把一个数位上的数值按要求平均分，如果有“余数”，就把它的计数单位变小和低一级上的数合并继续分。借助计数器不仅能形象直观地表达平均分的过程，更将思维聚焦在计数单位的转换上，沟通算理算法。

教学片段：

师：请说说52÷2=是怎么计算的。

师在黑板上贴出磁性计数器并在相应的数位下板书除法竖式。(见图1)

生：先分十位上的珠子，5颗珠子平均分成2份。

师：5颗珠子怎么平均分成2份？

生：分2份，一份2颗，还多1颗。

师：这一步除法竖式怎么写？

生：十位上商2，二二得4，写在5的下面，5减4得1。

师：2为何写在十位上？余数1写在哪位上？

生：因为这5颗珠子在十位上，表示50，平均分两份，每份是20还余10，所以这里的商2和余数1都要写在十位上。(见图2)

师：这位同学讲得真好，那么接下来怎么分呢？

生：将十位上剩下的1颗珠子移到个位上变成10颗珠子。(见图3)

师：单位变小一级，数量就变多了，十位上的一个1就是个位上的10个1，接着怎么分？

生：移过来的10颗珠子和个位上原来的2颗珠子合起来共12颗珠子，平均分成2份，每份6颗。

师：讲得真好，那么这一步在竖式上怎么表示？

生：个位上商6，2×6=12，12-12=0，没有余数。(见图4)

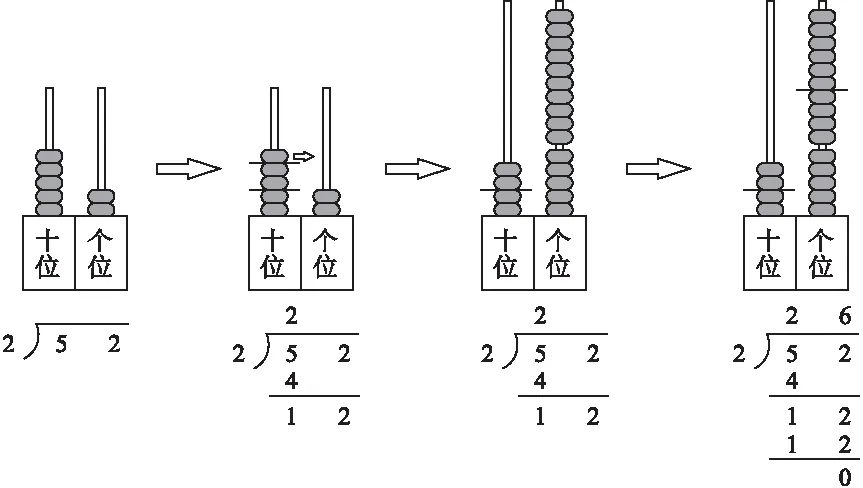
图1 图2 图3 图4

在教学中，我通过在计数器上分珠，将抽象的算理直观化，借助计数器这一教具，引导学生将“分—换—合—再分”的操作过程与竖式除法运算中的“除—余—合—再除”的计算过程建立联系，这样学生就很容易明白算理。

算法是算理的语言表征，是对计算方法的语言概括。在教学中我有意识地将除法竖式写在计数器下面，数位相对，让学生感受到“除到哪一位，商就上在哪一位”。同时“巧”用计数器，打破计数器上每个数位上珠子数不能破十的限制，直观呈现“上一位的‘1’换成下一位的‘10’”，凸显了“计数单位转换”这一核心，有效说明“如果有余数，要以‘1’当‘10’，和下一位上的数合起来再除”这一算法。

二、以计数器建联系，形成数学思想

(一)建立竖式除法和口算除法的联系

以下是我在教学中的一个教学片段：

师：同学们，比较这个算式的口算和竖式计算过程，你想说什么？

学生思考，讨论。

师提示：我们要结合竖式除法过程中计数器的拨珠过程观察。

生：口算和竖式计算的道理是一样的。

教师及时给予肯定，根据学生的回答，结合计算器完成以下总结(见图5)：

图5

不难看出，用计数器作媒介，学生很容易看出口算除法和竖式除法虽表达形式完全不一样，但实质上都是先将被除数按数位进行拆分，再分别进行平均分。

(二)建立竖式除法和竖式乘法的联系

教学片段如下：

师课件出示练习：根据下图计数器所表示的含义写一道竖式乘法和一道竖式除法。(见图6)

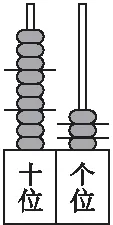
图6

学生练习，讨论。

请两名同学分别上黑板写竖式乘法和竖式除法,师生共同总结结果如下图7：

图7

师：你发现了什么？

生：我发现同一幅计数器示意图所表示的竖式乘法和竖式除法是相互联系的。它们是逆运算。

“联系”是一种重要的数学思想，教学中，我充分利用计数器建立竖式除法和口算除法以及竖式乘法之间的联系，有效渗透这一数学思想教育，深化学生对竖式除法的认知，让学生体会到小学数学知识是一个整体。

三、用计数器巧破疑，使教学更深入

在教学中，我们要重视学生的疑问，因为学生的疑问往往是学生没有弄懂的知识点，也是学生思维的生长点。

在课堂交流环节，有位喜欢动脑的学生问道:“老师，原先的竖式计算都是从低位算起，为什么竖式除法非要从高位算起？”此问一出，学生们都小声议论起来。看来这个问题引起大家的共鸣，我要抓住这个契机进行深度教学，接着进行了以下教学。

教学片段如下：

师：前面我们计算42÷2=和52÷2=时都是从高位算起，现在请同学们利用计数器探究一下，它们能从低位算起吗？

学生探究，在本子上画计数器演示图和相应的竖式除法计算过程，师巡视并指导。

学生汇报：

生1出示42÷2=的计数器演示图及相应的除法竖式。

生1：我觉得42÷2=可以从低位算起。

师：请你告诉大家为什么？

生1：先分个位上的2颗珠子，除以2，每份是1颗，正好分完，在个位上商1；再分十位上的4颗珠子，除以2，每份是2颗，正好分完，在十位上商2。合起来商为21。

师表扬，提高语气道：“那竖式除法可以从低位除起吗？”

生2：不能，我觉得52÷2=不能从低位除起。

师：请你来告诉大家为什么。

生2出示52÷2=的计数器演示图及相应的除法竖式。

生2：从个位算起，个位上2颗珠子，除以2，每份1颗珠子，这一步没有问题，但接下来算十位时，十位上的5颗珠子除以2，每份2颗，还余1颗，不能除尽，这余下的1颗珠子我又把它移到个位上，换成个位上的10颗珠子，进行二次平均分，这样计算太麻烦了，还容易算错，没有从高位算起来简便。

师鼓掌，道：同学们，现在你们觉得竖式除法是“从高位算起”好呢，还是“从低位算起”好呢？

生3：“从高位算起”好。

师：请你说说理由。

生3：因为“从低位算起”对于有的除法算式可行，有的不行；而“从高位算起”则对于任何除法算式都可行。

师：我也赞成这位同学的观点，竖式除法是一种计算方法，作为一种计算方法，我们就要选择最优算法，所以我们选择“从高位算起”。

以上教学中，教师引导学生利用计数器进行自主探究，在探索中思考，在思索中感悟，解决了疑问。学生的学习由此引向深入，思维得到延伸，真正的学习自然而然发生。

总之，由于计数器的引入，竖式除法的课堂教学令人耳目一新，走出了计算教学常有的说教模式，不仅变得生动活泼，更增加了课堂教学的宽度和深度。在这里，计数器不仅能直观形象地表征竖式除法的算理，表达算法，还是沟通数学知识竖向及横向间联系的有效手段和工具。它已成为学生深度思维的载体——以“计数器模型”来解决数学问题，成为学生思考数学问题的一种思维方式。