基于图像处理技术的高鲁棒性角膜曲率测量方法

黄铭斌，陈 隆，黄沃杰，郑伊玫，丁文正

（1.佛山科学技术学院机电工程与自动化学院，广东佛山 528225；2.佛山科学技术学院 物理与光电工程学院，广东 佛山 528225）

角膜是人眼结构前端的透明组织，其屈光力占人眼屈光系统的80%以上［1］，而角膜曲率半径决定着屈光度的大小，通过测量角膜曲率半径可以判断人眼有无杂散光以及近视的情况，同时也为角膜屈光度矫正手术和验配眼镜提供科学的判断依据［2-3］。

目前研究最多的角膜曲率测量方法是：采用一组同心圆的LED 阵列作为发光光源，发射出来的均匀光束照射到角膜上，经过角膜反射到成像系统中，被CCD 相机接收。根据像与像之间的几何关系，便可计算出角膜曲率半径［4-5］。现有的角膜曲率测量系统采用的图像处理方法基本都是直接对图像进行图像阈值分割处理［6-8］。在实际测量过程中，需要对人眼角膜最清晰的位置进行拍摄，对于眼睛小、睫毛长等不好处理的角膜图像，无法较好地滤除瞳孔外的眼部结构以及图像中的噪点，这些噪点会影响系统对靶环像的拟合结果，导致系统的测量精度下降，其鲁棒性都不是很高，并不具备市场运用价值。

为解决上述问题，本文基于图像处理技术，提出了一种新的角膜图像处理方法。该方法先对图像进行归一化处理，提高图像的对比度，再利用阈值化处理求取瞳孔区域；对原始图像采用大津法OSTU［9-10］对图像进行二值化处理，减去瞳孔外部的最大连通区域，再对获取的二值化图像与瞳孔区域图像求积，获取只有靶环像的二值化图像；最后采用了最小二乘法对靶环像进行拟合，求取椭圆的中心坐标、短轴、长轴和轴位角参数，通过角膜曲率的计算原理，计算出角膜曲率半径。该方法能较好地滤除图像背景带来的干扰，提高了系统的鲁棒性，对于人眼查找及角膜曲率测算具有一定的应用价值。

1 人眼角膜曲率测量系统及原理

角膜曲率测量的原理［11］如图1 所示，采用670 nm 的LED 灯阵列照射靶环，使光束形成均匀的同心光环在角膜上成像，根据角膜中央曲面直径大约4 mm 的位置近似一个球面透镜原理［12-13］，该同心光环会在角膜上成一个缩小正立的像，利用成像系统对角膜上的光环像进行捕捉，通过CCD 进行采集成像。由于获得的图像是一个眼睛的图像，需要滤除眼睛，对瞳孔内的光环进行提取，才可以对光环进行椭圆拟合。

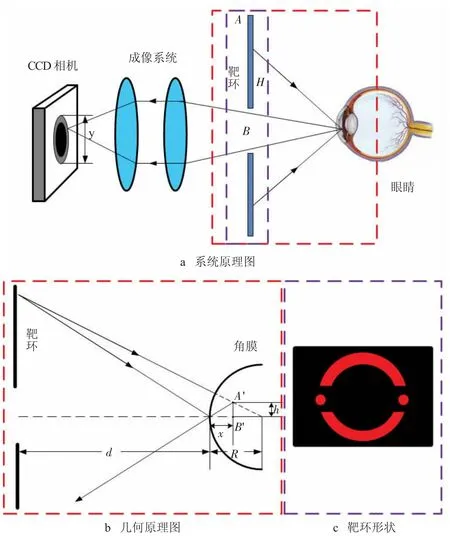
图1 角膜测量系统及原理

根据图1b 所示的LED 靶环与角膜之间的几何关系推导可得角膜曲率半径的表达式为

其中，R 为角膜曲率半径，d 为角膜到靶环间的距离，y 为CCD 上像的高度，β 为成像系统的放大倍数，H为靶环实际高度。靶环的高度H 是机械确定的标准参数，角膜到靶环的距离d 可通过光学相干层析成像原理进行测量，成像系统的放大倍数β 可通过将标定板置于焦深内进行测量，像的高度y 可通过对靶环进行最小二乘法拟合获得。由于d 的测量数值和y 的测量数值对系统精度的影响都比较敏感，本文使用的系统对d 的测量是基于时域光学相干成像系统，利用标准件的曲率半径对d 的值进行校准，然后通过测量角膜的干涉信号的位置，实时对角膜曲率进行测量。

图1c 为该角膜曲率系统的靶环形状，使用的是一个同心圆环，y 的精度取决于图像是否滤噪完全，光环的像能否完整的保留。在对光环进行拟合的过程中，如果角膜没有散光，相机接收到的成像则是一个同心圆环；而在有散光的情况下，相机接收到的成像将是一个同心的椭圆环。为了使拟合椭圆环的长轴、短轴和轴位角［14］等参数获得较高的精度，利用这些参数精确计算角膜的散光情况，需要设计一套具有高鲁棒性的图像处理方法。

如图2 所示，对椭圆拟合需要提取同心光环的内环和外环，用最小二乘法分别对提取出的内环与外环进行椭圆拟合，得到拟合系数，并利用求得的系数分别计算长轴、短轴、椭圆中心坐标和轴位角。

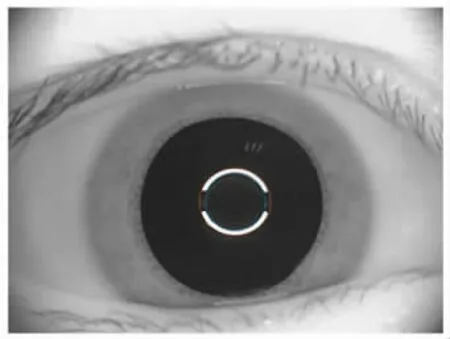
图2 角膜椭圆拟合图

拟合的椭圆方程一般设为

椭圆拟合的精确度用测量误差的平方和来描述，误差最小即拟合精度最高，误差函数为

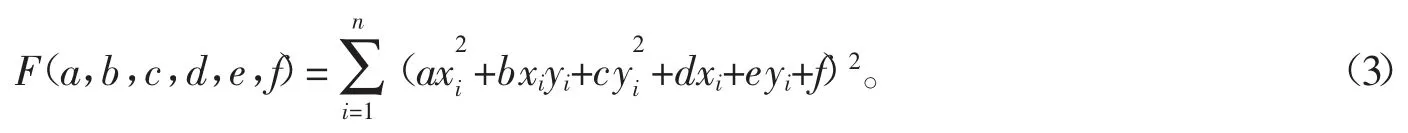
根据极值定理，为求取误差函数最小，则令各系数偏导为零，即

通过计算得到

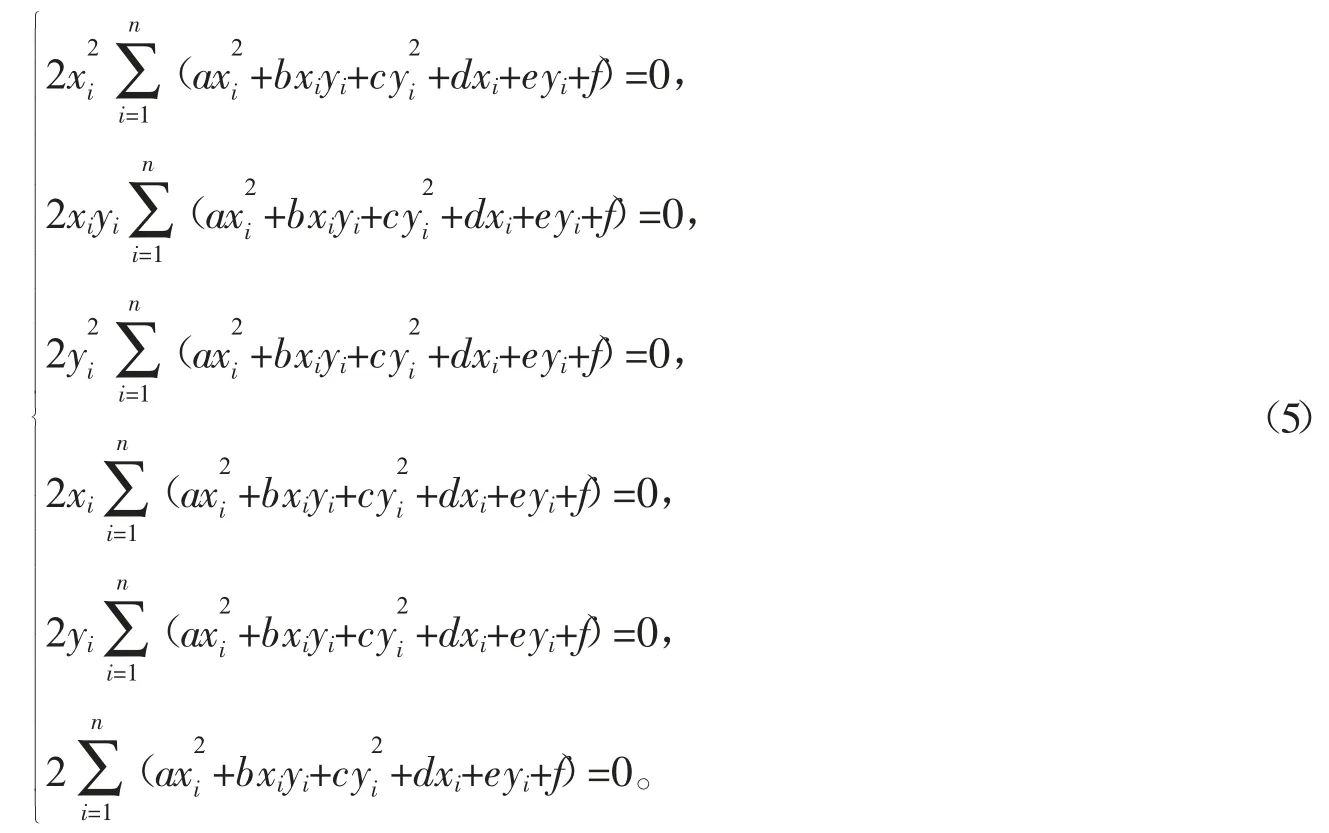
根据式（5）可以求解a，b，c，d，e，f 这5 个系数的值，求出椭圆系数后，利用这些系数代入下式便可求出中心坐标（xc，yc）、短轴a、长轴b 和轴位角θ，再根据这4 个参数确定拟合的椭圆。

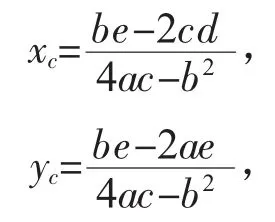
上述方法用于拟合椭圆可以得到式（2）中所求参数的最优解，根据靶环形状，分别拟合内环椭圆和外环椭圆，将计算出来的两个短轴长度和两个长轴长度取平均代入式（1）中，就可以精确计算出角膜的曲率半径和散光轴位角。

2 高鲁棒性角膜图像处理方法

为准确提取出角膜上靶环的像，滤除背景带来的干扰，提高系统的鲁棒性，准确拟合靶环的像，本文提出了一种新的图像处理方法来滤除背景，消除图像噪点给靶环像拟合带来的干扰。图3 是拟合LED 靶环的图像处理流程。该方法先利用式（6）对图像进行归一化处理，以提高图像的对比度

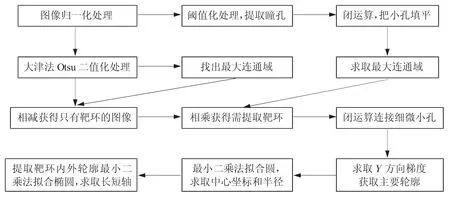
图3 图像处理流程图

其中，imgg 是归一化的图像，img 是一个x×y 个像素点的图像，min（img）为图像的最小值点，max（img）为图像的最大值点。针对瞳孔的特点，选取阈值，对角膜图像进行阈值化处理，提取出角膜中的瞳孔部分。为了获得只有瞳孔的二值化，滤除瞳孔内的靶环亮斑，对阈值化处理后的图像进行闭运算处理，将瞳孔内部以及外部的细缝填平，形成多个连通区域。然后通过求取图像中的最大连通域，提取出只含瞳孔的二值化图像。

大津法全称为OTSU-最大类间方差，是一种自适应的阈值确定方法，利用该方法对归一化后的图像进行阈值化处理，将靶环的像保留下来。利用闭运算处理，将瞳孔外面的部分连通起来，通过减最大连通区域滤除大部分的图像噪点。处理后的图像还可能会含有噪点无法滤除，通过将处理后的图像与只含瞳孔的二值化图像相乘，便可将瞳孔外部的噪点全部都滤除，而得到的靶环像可能会因为睫毛的原因而不够圆滑，所以需要对图像进行闭运算，将细孔填满，最终得到完整的只含靶环像的图像，最后对内环和外环进行椭圆拟合。

在对靶环像拟合椭圆时，需要再对处理后的图像进行Y 方向的梯度求取主要轮廓，减少运算量，便于利用最小二乘法对提取出来的靶环的像进行椭圆拟合，求取内、外环的中心坐标、长短轴以及轴位角，最后通过角膜曲率的原理计算出角膜曲率半径以及散光情况。

3 实验结果分析

在对眼球进行测量时，采集下来的图像会有角膜以及眼睛结构带来的干扰，为了滤除这些干扰，精准提取出完整的靶环像，提高椭圆拟合的精度，本文利用搭建好的角膜曲率测量系统，如图4 所示，对采集下来的眼睛测量图像进行处理。

图4 角膜曲率测量系统

为了验证算法的可行性，实验对无散光人眼图像进行采集，测试是否可以滤除角膜背景结构，精准提取出靶环的像。如图5 所示，利用该方法对人眼图像进行处理，可以较好地对瞳孔区域进行捕获，并提取出只含靶环像的图像，滤除角膜结构带来的干扰，实现对靶环的高精度拟合。

图5 图像处理效果图

由于部分人的眼睛存在眼睛小、睫毛长的问题，在测量时眼球多动，这些不定性因素都会导致图像噪点多，图像模糊，以至于在进行椭圆拟合过程中，无法很好地对靶环进行拟合。利用该图像处理方法可以很好地滤除这些问题带来的干扰，有利于提高椭圆拟合的精度。图6a 中采集的人眼瞳孔部位较为模糊，而且眼睫毛也较长，基本将整个角膜给挡住，在进行阈值化处理后，如图6b 所示，因为睫毛的原因会导致图中产生多个连通区域，通过闭运算处理，将大部分细微的噪点滤除，选取最大连通区域，得到完整的瞳孔区域如图6c 所示，去除掉瞳孔外较多的噪点。利用大津法OTSU 得到眼球的二值化图像，图6d 中瞳孔外还存在小片的连通区域，通过减最大连通区域并无法将其滤除，通过使用与瞳孔求积，得到只含靶环像的图，较好地滤除瞳孔以外的图像噪点。最后对靶环像进行闭运算处理，得到较为完整的靶环图像，如图6e 所示。图6f 为椭圆拟合后的图像，结果表明，该方法可以很好地滤除靶环像外的所有噪点，具有较高的鲁棒性，可以精确地对靶环内环和外环进行拟合，对提高角膜曲率半径的精度有较好的辅助作用。

图6 瑕疵眼球处理

为验证方法可以提高系统的拟合精度，实验利用曲率半径为8.005 mm 的标准件进行20 次测量，测量结果如表1 所示。根据实验数据可以得到，系统的误差值为±2 μm，重复性精度远高于国家计量规定的角膜曲率半径±0.02 mm 的最小误差，系统的平均值为8.002 9 mm，与标准值8.005 相差2.1 μm，该方法具有高精度的特点。

表1 测量半径约为8 mm 的20 组钢球的曲率半径mm

4 结语

为了解决现有角膜曲率测量方法的低适应性问题，本文提出了一种新的人眼角膜图像处理方法。该方法是先对图像进行归一化处理，计算出图像的最大连通区域，提取出瞳孔区域，再采用Otsu 大津法对图像进行二值化处理，通过与瞳孔区域求积，较好地滤除瞳孔外所有的噪点。最后对图像处理的结果图用最小二乘法拟合同心光环的内环和外环，计算出椭圆的短轴和长轴，并推算出角膜的曲率半径。利用该处理方法对图像进行处理，可以很好地滤除角膜组织给予图像带来的干扰，对系统具有较高的鲁棒性，可以精确提取靶环，对靶环进行拟合；采用曲率半径为8.005 mm 标准件进行实验，实验结果表明，本文提出的方法实现了系统误差±2 μm，系统重复性良好，平均值为8.002 9 mm，比标准值小了2.1 μm，远高于国家计量规定的角膜曲率半径±0.02 mm 的最小误差要求，具有较高的精度标准。该方法对角膜曲率测量仪器的研究具有重要的市场应用价值，对提高角膜曲率精度具有重要的意义，有利于推动眼科医疗行业的发展，在图像处理领域具有一定的参考价值。