社会网络环境下基于群体一致性的概率语言多属性大群体决策方法
2022-08-02张发明朱姝琪
张发明,朱姝琪
(桂林电子科技大学 商学院,广西 桂林 541004)
当多名决策者必须根据预定义的属性集,从不同备选方案中选择出最佳方案时,即面临多属性群决策问题[1]。随着社会及互联网技术的快速发展,群体决策者的规模及其决策复杂度也在不断增加,相关研究学者已经注意到多属性大群体决策问题[2-3]。Chen等[4]认为当决策群体成员的数量超过20人时,即可称其为大群体。作为多属性群决策问题的衍生,现阶段关于多属性大群体决策问题的研究仍处于起步状态[2],相关研究已经取得了一些研究成果[5-10],其中多数学者尝试通过聚类算法对多属性群决策问题进行分组降维,以实现简便计算。Palomares等[11]提出一种基于FCM 聚类算法的大群体决策模型,对大群体决策者进行分组以实现有效降维。Liu等[12-13]提出一种部分二叉树DEA-DA循环分类模型对决策者进行分类处理,通过连续区间有序加权平均(COWA)算子汇总表现为区间值直觉模糊数的评价信息。Wu等[7]针对区间Ⅱ型模糊集,提出一种基于模糊等价聚类和语言信息聚类的群决策聚类方法,用于聚合决策者的偏好。上述研究为降低多属性大群体决策问题的决策复杂度提供了一定的理论支持,但这些研究并未对大群体决策者的共识过程做过多探讨。事实上,随着群体决策者数量的增加,获得大规模群体共识意见的难度也在大幅提高,共识问题成为解决多属性大群体决策问题的关键要素之一。目前,已有学者尝试从不同角度探讨多属性大群体决策的共识达成问题。Tang等[15]考虑大群体决策者之间的群内和群间共识水平,提出一种基于模糊C-means聚类算法的自适应共识模型,并根据子群大小和内部聚合度确定群间权重。Wu等[6]基于可能性分布的犹豫模糊元(PDHFE),提出一种基于K-means聚类方法的共识模型,以实现对大规模群体决策者的降维和聚类。Labella等[16]开发出一款基于共识分析框架的AFRYCA 2.0软件,旨在模拟出不同的共识模型性能以及共识达成过程中不同专家的行为模式。值得注意的是,上述研究大都是在假设大规模群体决策者彼此之间相互独立的前提下开展的,尚未虑及群体决策者之间存在的社会关系及其内部联系。
在现实决策中,大群体决策者的社会网络特征及其之间的社会关系会对大群体决策的聚类效果和决策结果造成一定的影响[17-18]。考虑社会网络关系的多属性大群体决策问题的研究,更能契合实际决策的需要[6,37],一些学者开始尝试引入社会网络关系来解决多属性大群体决策问题。Chu等[19]提出一种基于模糊聚类的社会网络社区检测方法,依据社区划分的不完全模糊偏好关系补全缺失信息,通过社区网络的度中心性确定权重。Wu等[7]针对区间Ⅱ型模糊集,提出一种基于Louvain社区探测方法的大群体决策模型,根据社区网络特征确定决策者及社区子模块权重。Tang等[20]考虑群体决策者之间的社会网络关系,提出一种基于最大共识序列的大群体决策方法。值得注意的是,上述基于社会网络关系的多属性大群体决策问题的研究中,大都重点关注大规模群体决策者的聚类问题,较少同时考虑多属性大群体决策问题的聚类分析和群体共识的反馈调整过程。同时,上述研究都是基于一个专家只能隶属于一个社区或集群的假设基础上,直接对群体决策者进行聚类分析或降维,较少考虑现实情境中存在决策者同时隶属于多个子群参与决策的情况[20]。事实上,在现实决策中,由于决策者具有多样性,一名决策者往往可以隶属于不同类别的集群参与决策,即存在重叠社区[21-22]的情况,例如在实际情况下,某名决策者依据其多重社会属性,既可以隶属于教授群体参与决策,又可以隶属于行政人员群体参与决策。因此,研究具有重叠社区属性特征的多属性大群体决策问题具备一定的现实意义和理论价值[23]。
在研究多属性大群体决策问题时,如何准确表达群体决策者的个体偏好特征也是学者关注的重点[24-25]。相关学者尝试基于概率犹豫模糊集[26]、区间Ⅱ型模糊集[7]、犹豫模糊偏好关系[20,27]等信息偏好表达形式来解决多属性大群体决策问题。概率语言术语集(PLTSs)[28]作为近年提出的偏好表达形式,通过引入概率信息来反映决策者对不同语言术语集的偏好程度,能够更好地满足实际评价与决策的需要。因此,本文重点探讨偏好表达为概率语言信息的多属性大群体问题,允许专家使用概率语言来表达个人偏好信息。
基于上述分析,本文针对社会网络环境下,决策者偏好表达为概率语言信息的多属性大群体决策问题,提出一种新的、考虑重叠社区属性特征的概率语言多属性大群体决策方法。为使最终决策方案更符合现实需要,首先考虑大群体决策者之间的社会关系,对具有重叠社区属性特征的社区子模块进行预处理,然后改进Louvain 社区探测算法(Modified Fast Louvain Method,MFLM)以解决概率语言多属性大群体决策中的聚类及社区子模块划分问题,依据群体意见的一致性及其社会网络关系来确定各节点及社区子模块的权重。进一步,引入最大共识序列挖掘算法用于解决概率语言多属性大群体决策问题,在考虑群体决策意见一致性的基础上,提出一种基于概率语言信息的大规模群体共识测度和反馈调整方法,从而根据最终的共识比较序列确定最优评价方案。
1 预备知识
1.1 社会网络分析
在社会网络中,人们通过彼此之间存在的各种社会关系实现相互关联,一般用一组节点e和一组边l组成的集合表示。节点e可以表示任一社会行为主体(如个体、组织、国家等),边l则用来表示各节点e之间的关系(如信任、友谊、合作等),一般用有向图G=(e,l)表示。其中,边l具有方向性,依据实际情况,节点之间存在单向连接、双向连接及不连接3种情况[29]。本文将单向连接和双向连接两种情况做统一处理,选用无向社会网络图进行分析,即节点之间仅存在有连接和无连接两种情况。令E={e1,e2,…,em}表示m名决策者集合,在社会网络关系中,中心性是衡量节点ek(ek∈E)重要程度的有效标尺,关于节点ek的度中心性C(ek)表述如下:
定义1[30]与节点ek相连接的节点数被称为节点ek的度,则节点ek的度中心性可表示为

式中:m为社会网络的总节点数,即社会网络中群体决策者的数量;G是社会网络关系矩阵。
1.2 概率语言
定义2[28]设S={Sα|α=-τ,…,-1,0,1,…,τ}为一个语言术语集,其中,Sα表示语言术语,则概率语言术语集可表示为

式中:L(k)(p(k))表示概率为p(k)的语言术语L(k);#L(p)为概率语言术语的数量。特别地,当时,此时语言术语的概率信息完全未知,原概率语言术语集退化为犹豫模糊集,故对此类情况不做详细探讨。
为方便比较两个概率语言术语集的大小,现引入概率语言术语集的期望函数和偏离度函数进行度量。
定义3[28]设r(k)为概率语言术语L(k)的下标,则概率语言术语集L(p)的期望函数和偏离度函数分别为:
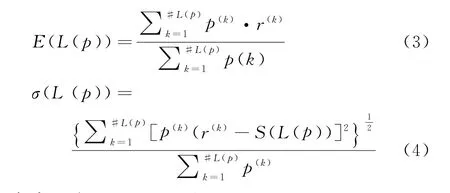
式中,对于L1(p)和L2(p)(L1(p),L2(p)∈L(p))的比较规则如下:
(1)当E(L1(p))>E(L2(p))时,则称L1(p)≻L2(p)。
(2)当E(L1(p)) (3)当E(L1(p))=E(L2(p))时,则有:当σ(L1(p))<σ(L2(p))时,称L1(p)≻L2(p);当σ(L1(p))>σ(L2(p))时,称L1(p)≺L2(p);当σ(L1(p))=σ(L2(p))时,称L1(p)~L2(p)。 定义4[31]令r(ki)i表示Li(p)中第ki个概率语言术语的下标,则任意两个概率语言术语集L1(p)和L2(p)(L1(p),L2(p)∈L(p))的距离为 式中,#L(p)=#L1(p)·#L2(p)表示L1(p)和L2(p)数量的乘积。 在实际决策中,由于决策者具备不同的社会属性,一个决策者可能隶属于不同的决策群体参与决策,具体示意如图1所示。 图1 重叠社区子模块示意图 考虑大规模决策群体可能存在的社区子模块重叠性网络特征,更能满足现实复杂决策的需要[32]。对于现实决策中存在的具备社区重叠特征的大规模群体决策者,需要对其进行预处理,将其重新划分至非重叠的社区子模块,以便进行后续处理。为更好地对存在社区子模块重叠特征的大规模群体决策者进行预处理,定义社区子模块的模块中心性M(Nf)[30]和社区子模块隶属度Dk如下: 定义5[30]设社区子模块的模块中心性为 式中,N={N1,N2,…,Nn}表示社区子模块的集合(Nf∈N)。 定义6设社区子模块隶属度为 对于具有重叠社区属性特征的决策者ek,计算其位于各重叠社区子模块的隶属度,并进行比较,根据比较结果将其划分至第f个社区子模块,同时将其从其他重叠子模块中剔除。重复上述步骤,直至社区网络中不存在重叠社区。 MFLM(Modified Fast Louvain Method)方法是一种用于提取社区网络信息的强大检测工具,是在Louvain方法基础上的进一步优化和改进,常用来探测复杂社会网络的底层结构。将其应用于多属性群决策问题中的大规模群体聚类,能够有效揭示大规模群体社会网络中的层次和结构。具体步骤如下[34]: 步骤1相似度检测。在步骤1中,社区网络中的每个节点e都被视为是一个单独的个体社区,则在初始状态下,社区的数量等于网络中所有节点的数量。 定义7令e和c表示社区网络中任意两个节点,则相似度测量系数可表示为 式中,τ(e)和τ(c)表示节点e和c的邻域。 定义8令任意两个节点之间的平均共享得分函数为 式中:h为节点e和c的共享链接数;ke和kc为节点e和c的度;m为社区网络中的链接总数。 为使每个节点e均能找到最佳的社区子模块归属,计算其对应的c个相似度测量系数Dec,确定max(Dec),将节点e分配至其相邻社区。上述过程对每个节点持续迭代,直至社区子模块不再发生变化。 步骤2社区子模块优化。计算社区子模块的模块化得分,通过比较社区子模块的模块化得分判断所划分社区结构的优劣。 定义9令社区子模块得分函数为 式中,w为连接节点e和c的边权重。 步骤3社区聚类。将隶属于同一社区子模块的节点抽象为一个总节点,令边权重为1,重新计算社区网络中的点权重及边权重。重复上述步骤,直至获得最高的社区子模块分数且社区子模块不再发生变化。 在社会网络关系中,决策者的权重主要是通过衡量各群体决策者之间的重要程度来确定的。决策者的度中心性越大,说明与该决策者产生关联的决策者就越多,则该决策者的重要性也就越大[30]。决策者节点ek基于度中心性的权重可表示为 在群决策问题中,隶属于不同社区子模块的决策者通常具备不同的知识背景及个人偏好,则需要充分考虑各社区子模块偏好信息,以确定相应的权重。通常情况下,社区子模块中群体决策者的偏好意见越集中,说明该社区中群体决策者的方案偏好一致性越强,其相应模块的权重就应当越大。同时,引鉴古代“三个臭皮匠,赛过诸葛亮”的思想,社区子模块中划分的群体决策者数量越多,其对应的子模块权重也应当越大。 定义10令Tf表示社区子模块Nf的得分函数,规定社区子模块Nf的一致性函数为 式中,社区子模块的一致性水平If越高,该模块决策者的方案偏好一致性越强。 定义11社区子模块Nf基于群体一致性的权重的计算公式为 社区子模块Nf基于分区群体决策者数量的权重计算公式为 则社区子模块Nf的综合权重为 式中,ρ(0<ρ<1)为权重调节因子,可以根据实际情况由决策专家拟定。 3.2.1 共识方法 现有的多属性群决策共识模型大都是基于相似度或群体意见的离散程度来度量群体意见的共识水平,通过不断搜集反馈信息来调整群体决策者的偏好,目的是降低群体意见之间的差异程度,直至达成群体共识[18-20]。然而,在现实社会网络中,由于群体决策者知识背景、决策偏好等的差异,不同决策者给出的评价信息可能会存在较大差异。为降低概率语言多属性群决策过程中可能存在的少数极端值对决策结果的不良影响,在参考文献[20,34]的基础上,将最大共识序列挖掘算法拓展至概率语言大群体决策领域,旨在通过不断迭代发现尽可能长地与多数意见保持一致的共识方案序列,得到群体决策者的最大共识水平,以最终得到方案的优劣排序。设A={A1,A2,…,At}(t≥2)为备选方案集,E={e1,e2,…,em}(m≥20)为m名群体决策者的集合,C={C1,C2,…,Cb}(b≥2)为方案属性集,N={N1,N2,…,Nn}为划分的n个社区子模块集合,Nf∈N(f=1,2,…,n);xAp>xAq表示一组方案比较关系,称为一个方案对,其中Ap,Aq∈A,且当p≠q时,Ap≠Aq,{xA1>xA2>…>xAt}为一组方案比较序列,表示群体决策者对备选方案集的偏好程度。 定义12在概率语言多属性大群体决策问题中,定义群体决策者的一组方案偏好关系对xAp>xAq的社区子模块方案偏好度为 对于任意方案Ap(Ap∈A),对应群体决策者的最佳方案偏好度为 对于任意方案Ap(Ap∈A),其社区模块最佳方案共识度为 方案比较序列xA1>xA2>…>xAt的社区子模块方案偏好度为 方案比较序列xA1>xA2>…>xAt的共识度为 3.2.2 共识达成及反馈调整 令Zd表示长度为d的共识比较序列集合,比较序列中方案的个数即为Zd的长度。特别地,令Z1={xA1,xA2,xA3,xA4}。 输入大规模群体决策者提供的概率语言评价信息;共识度阈值P'。 输出达到大规模群体决策共识的决策方案序列。 步骤1通过以下算法迭代计算以生成大规模群体决策者的共识序列Zd。 步骤2识别Zd-1中的可连接序列并连接。例如,l1={xA1>xA2}和l2={xA2>xA3}为Z2中的共识比较序列,则连接l1、l2,得到l3={xA1>xA2>xA3}为Z3中的共识比较序列。 步骤3若d=t,则生成的Zt即为最终的共识比较方案排序;否则,转步骤4。 步骤4当d 基于上述分析,给出考虑具有重叠社区属性特征的概率语言多属性大群体决策方法步骤如下: 步骤1识别初始状态下大规模群体决策者的社区属性特征,若存在重叠社区特征转步骤2;否则,转步骤3。 步骤2根据式(6)~(7),对存在重叠社区特征的大规模群体决策者进行预处理,计算其社区子模块隶属度,将其划分至隶属度最大的社区子模块,同时从其他重叠子模块中剔除,重复直至社区网络中不存在重叠社区。 步骤3根据式(8)~(10),利用MFLM 社区探测算法对大规模群体决策者进行社区子模块的聚类划分,得到n个非重叠社区子模块{Nf|f=1,2,…,n}。 步骤4根据式(11)~(15)计算大规模群体决策者的权重wk及社区子模块权重wf。 步骤5根据概率语言多属性群决策共识方法,计算各方案比较序列的共识度。 步骤6根据共识达成及反馈调整模型,计算大规模群体决策者的最大共识序列或部分最大共识序列。 步骤7根据计算结果,确定最佳决策方案。 决策流程示意如图2所示。 图2 基于群体一致性的概率语言多属性群决策方法决策流程 现共有20 名来自多个领域的杰出专家E={e1,e2,…,e20}需要根据属性集C={C1,C2,…,C6},对4个备选方案A={A1,A2,A3,A4}进行多属性大群体决策,决策专家大群体所对应的评价语言术语集可表示为:S={S0,S1,…,S5},对应评语集为:{极差,较差,偏差,偏优,较优,极优},对应权重ω={0.1,0.1,0.3,0.2,0.2,0.1},共识度阈值为:P'=0.51。其初始社会网络关系如图3所示。 图3 决策专家社会网络结构 经处理后得到初始决策专家评价矩阵如表1所示。 表1 决策专家评价矩阵 步骤1根据决策专家的社会网络结构图(见图3),根据式(8)~(10),利用MFLM 社区探测算法对大规模群体决策者进行社区子模块的划分,划分结果如图4所示。根据社区网络分析理论,将20名决策专家划分为4个社区子模块。 图4 决策专家社区子模块示意图 步骤2根据式(11)~(15),计算决策者及社区子模块权重,计算结果如表2所示(取权重调节因子ρ=0.5)。 表2 专家及社区子模块权重 其中,根据式(11)计算得到社区子模块N1中对应的决策成员权重为:w1={0.11,0.22,0.17,0.22,0.28},社区子模块N2中对应的决策成员权重为:w2={0.27,0.20,0.13,0.20,0.20},社区子模块N3中对应的决策成员权重为:w3={0.16,0.21,0.21,0.26,0.16},社区子模块N4中对应的决策成员权重向量为:w4={0.17,0.22,0.22,0.22,0.17}。 步骤3根据共识方法,生成最大共识序列。已知Z1={xA1,xA2,xA3,xA4},根据算法1 生成Z'2。根据式(17)~(21),结合表2的权重系数及决策成员权重进行信息集结,计算d=2时各方案比较序列共识度水平,计算结果如下: 步骤4识别步骤3中共识度水平大于共识度阈值P'的的可连接序列并根据算法进行连接,得到Z3的共识比较序列为: 步骤5识别步骤4中Z3的可连接序列并连接,得到Z4的共识比较序列为:l4={xA2>xA1>xA4>xA3}。 步骤6由步骤5可得满足条件d=t=4,则生成的Z4即为最终的共识方案序列。 输出最终共识比较方案排序为:A2≻A1≻A4≻A3,确定最优方案为:x*=A2。 本文基于社会网络环境,考虑到现实决策中决策者存在隶属于重叠社区和非重叠社区的情况,提出了基于概率语言信息的大群体决策共识测度模型和共识调整方法。为充分说明本文方法的合理性及优越性,将本文方法与文献[20,35-36]中所提出的模型进行对比分析,主要集中在信息表达形式和聚类权重计算两个方面的展开。 (1)在评价信息的表达形式上,现有文献针对评价信息为概率语言术语的大规模群体共识序列挖掘算法与大群体决策模型结合的研究还相对较少,文献[20,35-36]中则分别是针对犹豫模糊信息、不完全概率语言信息、犹豫模糊元素等评价信息展开的相关研究(见表3)。相较于其他文献,本文方法考虑现实决策中社会网络关系的影响,对决策者隶属的重叠模块进行预处理,通过共识测度模型能直接导出共识结果,从结果来看,本文模型达成共识一致性的过程相对更加高效。 表3 不同群决策方法的对比分析 (2)在聚类方法的权重确定上,由于文献[36]中采用基于可能性分布的犹豫模糊元素(PDHFE)表示每个群组的偏好,无法直接应用到概率语言术语集领域,故引用文献[20,35]中的方法对本文算例进一步分析和计算,计算结果如表4所示。 表4 不同权重计算方法的比较结果 采用文献[35]中所提提出聚类权重确定方法对本文算例进行计算,得到:0.25),该方法基于聚类成员数量对聚类群体进行权重的计算和划分,但当聚类成员数目相同时,该方法难以体现不同聚类下各群体决策者之间的差异;采用文献[20]中所提出的子群权重确定方法对本文算例进行计算,得到:该方法综合考虑了社区子群内的专家数量以及子群内的链接强度因素,对聚类后的社区子群进行赋权,但该方法在集结权重指标时,采用直接将不同指标相乘再归一的处理方法,难以体现不同指标的重要程度。本文所提出的子模块权重确定方法基于群体一致性和不同聚类成员的数量进行计算,设置了调节系数,能够根据实际情况及时调整不同指标在聚类时的重要程度,更加符合实际需要,同时能够在聚类社区子群成员数量完全一致时,有效赋予社区子群权重,以更好地满足现实决策的要求。 除了上述两点外,对比文献在群体聚类方法和共识达成过程方面也存在较大不同。文献[20]中引用加权网络重叠社区探测算法对大群体决策者进行聚类划分,提出了基于重叠子群的共识达成方法,该方法可以较好地处理子群具有关联特点的群体决策问题,但该方法在确定不同的核心社区时可能会得出不同的聚类结果,较难保证大群体决策的鲁棒性。文献[35]中在闭包聚类的基础上,提出了两阶段专家相似度测度方法,该方法通过距离测度和距离赋权计算专家评价信息的差异值,可以较好地处理专家的聚类分析问题,但当决策群体数量或评价属性较多时,该方法关于评价信息距离的测度和距离权重赋权计算量就相对较大,较难很好地处理群体规模较大的聚类问题。文献[36]中采用K-means方法对专家大群体进行聚类,该方法需要人为规定聚类后的子群数目,这使得最终评价结果可能会受到一定的主观因素影响。同时,文献[35-36]中均需要对通过共识测度的群体评价矩阵进行再处理,根据计算公式集结出最终的优先级矢量,并根据计算结果进行排序。相比之下,本文采用的MFLM 社区探测算法是对Louvain方法的进一步改进和优化,将其用于解决大群体决策问题,不仅避免了提前确定子群数目对决策结果造成的可能误差,还可以有效揭示大规模群体社会网络中的层次和结构。同时,本文方法通过逐步迭代生成达到共识度阈值的群体共识方案序列,可以直接导出共识结果,根据共识序列即可确定最终方案,计算过程相对更加简便、高效。 传统大群体决策方法鲜少虑及现实决策中存在决策者隶属于多个社群参与决策的情况,且针对评价信息为概率语言的多属性大群体决策问题的研究还相对较少,针对上述不足,本文提出一种社会网络环境下基于群体一致性的概率语言多属性大群体决策方法及共识达成模型,为解决评价信息为概率语言的多属性大群体决策问题提供了一种新的、可供参考的借鉴思路。与现有文献相比,本文方法具有如下特点: (1)将社会网络分析理论拓展至概率语言多属性大群体决策领域,在确定决策者及社区子群权重时,考虑了群体决策者之间的社会关系,基于群体一致性和社区子模块决策者数量确定权重,使得计算结果更能满足实际决策的需要。 (2)考虑自然状态下存在群体决策者隶属于多个重叠社区的现象,对其进行预处理,采用MFLM社区探测算法自动聚类,无需提前设置社区聚类数目,避免了主观因素可能给决策结果带来的不利影响。 (3)提出的基于概率语言信息的共识测度模型在计算各比较序列共识测度的基础上,不断生成达到大群体共识阈值的比较共识序列,通过反馈调整,生成达到群体共识阈值的最大共识比较序列,从而得到最终的决策方案,无需集结最终的优先级矢量并比较排序,方法相对更加简便易懂。 由于传统多属性群决策问题假设专家之间相互独立,基于社会网络的多属性群决策问题假设专家之间相互关联,而在实际决策中存在部分专家相互独立,部分专家相互关联的情况[23],同时,考虑到决策者的评价语言信息具有多样性,未来研究可从进一步探究同时包含独立和不独立专家的大规模多属性群决策问题,以及将大群体决策的语言形式拓展至混合语言信息等方面展开。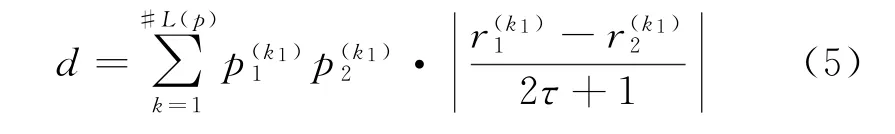
2 考虑重叠社区特征属性的模块预处理
2.1 重叠社区子模块预处理
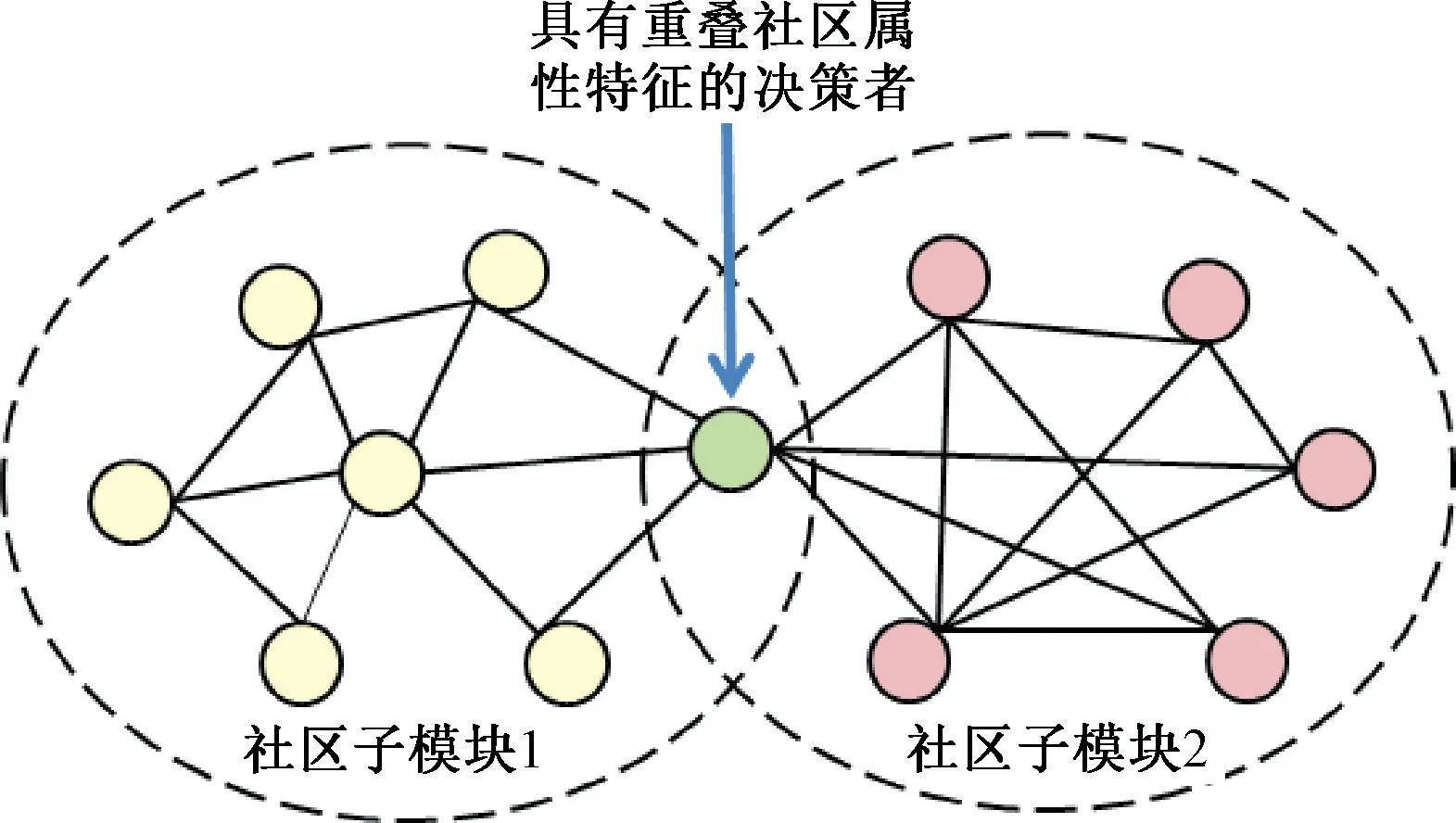
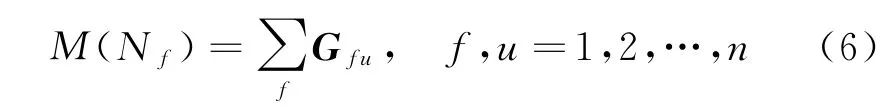
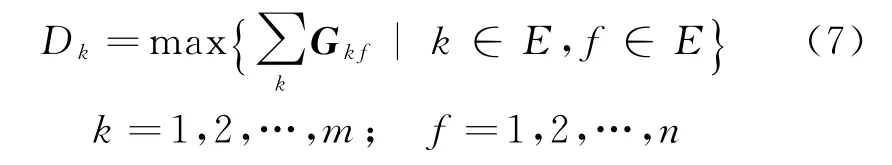
2.2 社区子模块划分

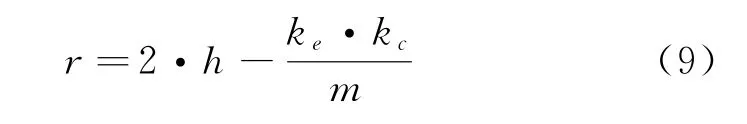

3 基于群体一致性的概率语言多属性群决策方法
3.1 决策者权重及社区子模块权重的确定
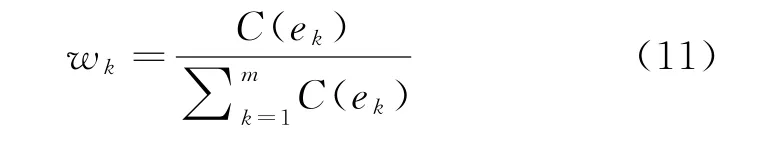
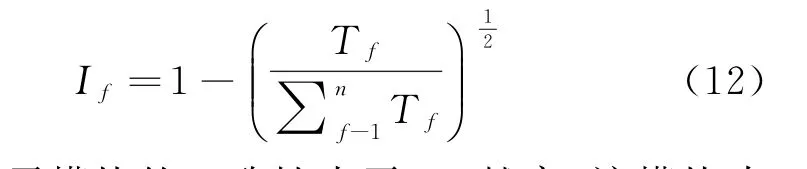
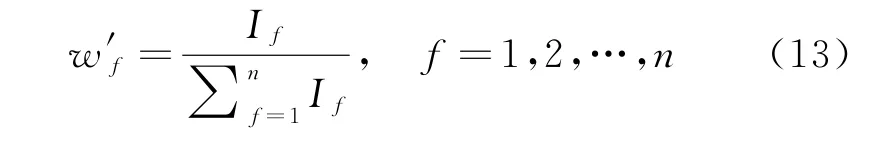
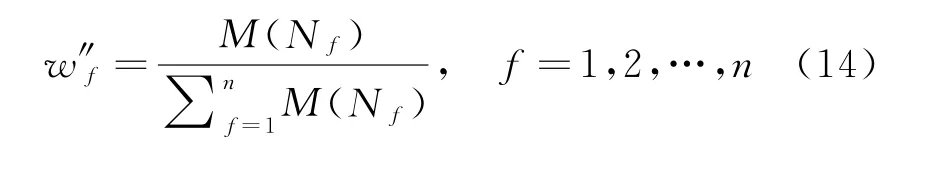
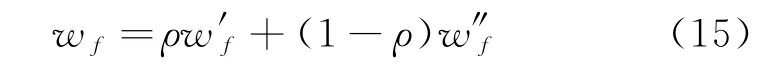
3.2 共识测度模型

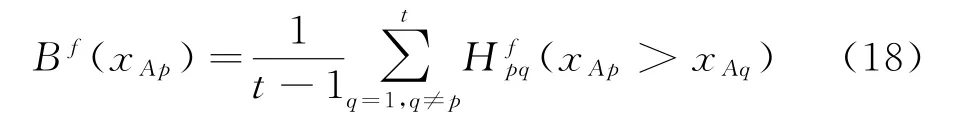




3.3 决策步骤

4 算例分析
4.1 问题背景

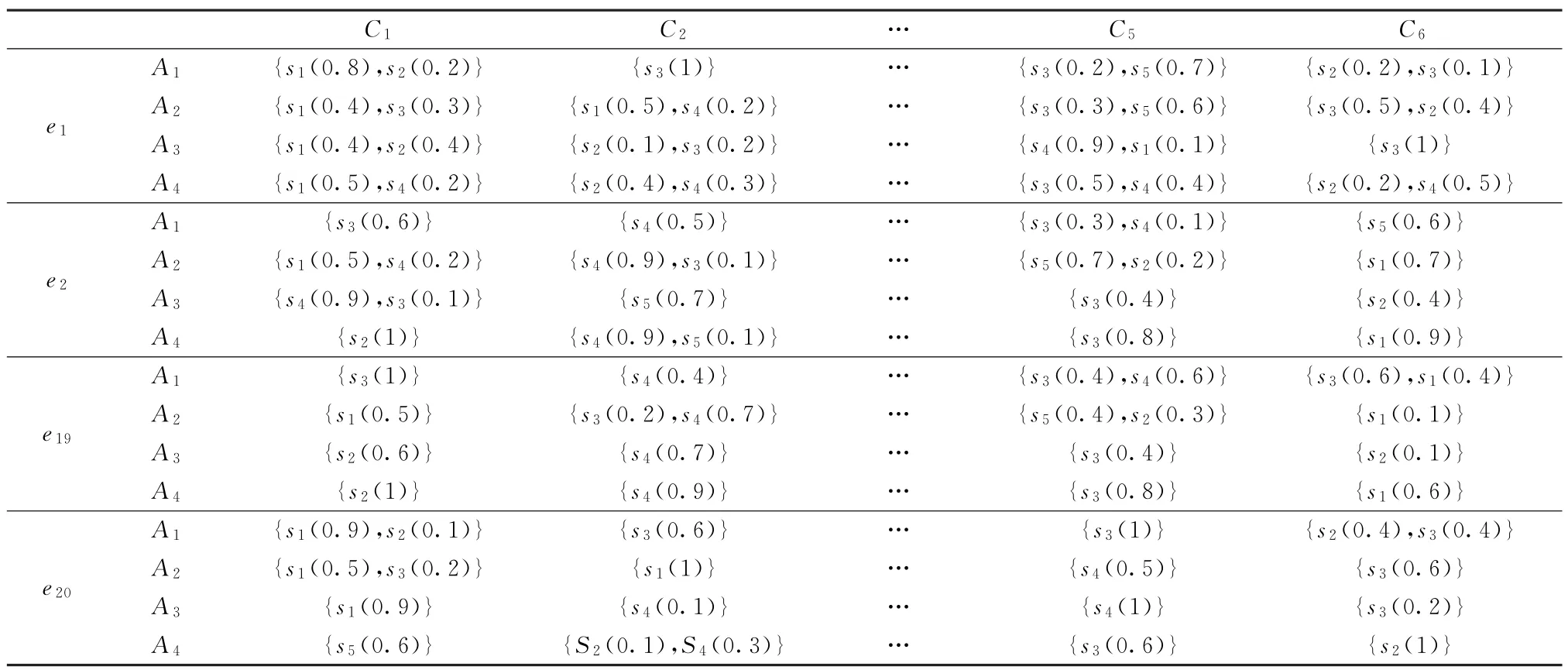
4.2 决策过程

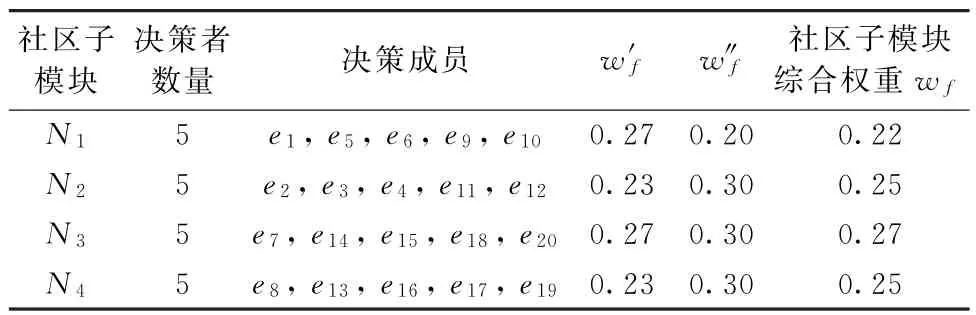
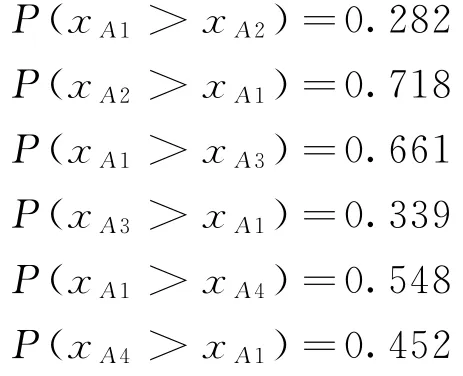


4.3 对比分析


5 结论
