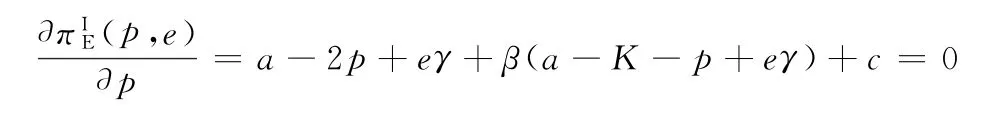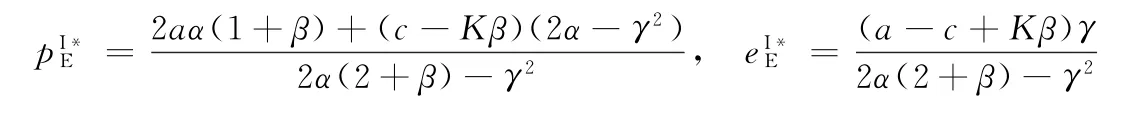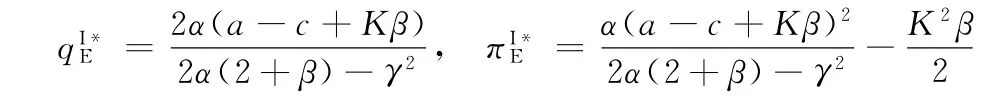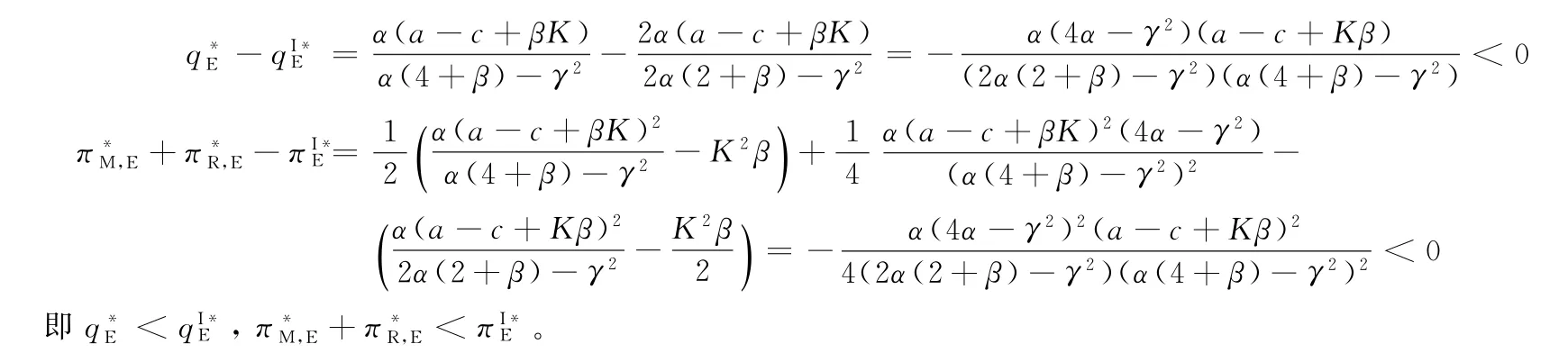考虑促销努力的供应链产能策略及其协调
2022-08-02汪婷婷
常 珊 ,胡 斌 ,汪婷婷
(1.湖北经济学院 信息管理学院 大数据与数字经济研究院,武汉 430205;2.华中科技大学 管理学院,武汉 430074)
在企业的生产运作过程中存在着供需不匹配的问题,例如劳动力、技术和设备、原材料、加工制造、办公场地和库存等的过剩或不足[1],这给企业的产能管理带来了挑战。产能过剩会导致资源浪费和低效率,产能不足会造成销售流失和信誉损失。因此,有效的产能管理不仅能更好地匹配供需,保障企业价值实现过程的高效性,还可以提高企业的市场竞争力。以物联网和云计算等新兴信息技术为基础的云制造模式[2]使得制造商的产能具有柔性——根据需求情况进行产能扩张。在供应链情境下,企业间决策彼此关联,制造商的产能柔性也必将受到其下游零售商相关决策的影响。因此,在供应链情景下研究制造商的产能柔性与零售商相关决策间的交互影响,不仅是理论上值得探讨的问题,同时也是实践领域需要解决的现实问题。
广告或促销是企业创造需求的重要工具[3]。作为直面消费者的零售商,其有实施广告或促销活动的强烈动机。零售商的价格调整或促销活动会影响市场需求,这种变化可能导致上游制造商的产能问题——产能过剩或不足。针对该问题,制造商可以采用不同策略加以应对。其一,制造商通过批发价影响零售商的价格或促销决策,从而间接影响市场需求,以缓解其产能管理问题;其二,制造商构建柔性产能,以产能扩张的方式应对因零售商营销策略引起的需求变化对其产能管理的影响。可见,零售商的价格和促销努力决策与制造商的批发价决策和产能策略之间相互影响。因此,当制造商的产能不具有扩张性时,零售商是否有实施促销的动机? 促销努力对供应链绩效有何影响? 当制造商的产能具有扩张性时,其是否会利用产能扩张来满足更多市场需求? 零售商的促销行为对供应链绩效又会有怎样的影响? 两企业间相互制约的关系是否会导致供应链中柔性产能的低效率? 是否存在契约能够协调供应链,使两个企业的利润都得到Pareto改进? 为回答上述研究问题,本文首先考虑制造商的两种产能策略,并分析零售商的价格或促销决策在不同产能策略下的影响;然后,基于供应链低效率的问题,通过设计合适的契约以协调该供应链。
1 文献综述
促销投入可以让产品购买者获得额外效用,从而增加该产品市场份额[4]。大量文献都在研究中考虑促销努力对需求的影响。在零售价格外生的假定下,Krishnan等[5]考虑了不确定需求下的库存决策和需求确定后的促销努力决策。其中,促销努力是通过相乘的方式影响需求,类似的研究还有文献[6-8]。Nouri等[9]则在模型中考虑零售商促销努力对需求的线性影响。上述研究均假设零售商是市场价格的被动接受者(没有定价权)。另外,在转售价格维持契约下,零售商也不能进行价格决策,只能通过促销努力影响需求[10-11]。在非完全竞争市场下,例如由制造商和零售商组成的双层供应链中,每个成员都是对应层级中的垄断者,拥有完全的定价权。Desai[12]认为需求是零售商增值服务的凹性增函数,是零售价格的线性减函数。文献[13-16]中均同时考虑促销和价格因素对需求的不同影响。在零售商的促销努力成本是私有信息时,Gurnani等[17]研究了制造商对不同契约的偏好。在促销成本和促销努力水平均不可知的情境下,Mukhopadhyay等[18]设计了最优契约激励零售商进行促销。不同供应链结构下的促销努力也得到学者关注[3,19-20]。
一旦在模型中考虑零售商的促销努力,传统的契约可能无法协调供应链。Krishnan等[5]的研究表明,回购契约会削弱零售商的促销动机,因此,需要结合促销成本共享等契约才能实现供应链协调。在双层供应链中,Ma等[21]设计了两部定价契约、促销成本和质量改进成本分担相结合的契约来协调供应链。Cachon等[22]考虑了存在零售商促销努力时收益共享契约的有效性问题,结果表明,促销效果的强弱会影响供应商对收益共享契约和批发价契约的选择。He等[23]发现,在依赖促销努力和零售价格随机需求下大多数契约都无法实现供应链协调,由此设计了组合契约进行协调。另外,相关学者研究了上游企业[24]、上下游企业同时实施促销努力的情况[25-27],但均未考虑产能或库存约束。
上述文献表明:①促销努力是实现需求增量(线性或非线性的)的重要方式之一;②促销努力的引入使企业的决策更加复杂(信息的不对称、协调契约的有效性);③促销努力与产能扩张相结合的研究还不充分。
关于产能投资问题,现有文献大多都是基于需求不确定性分析产能投资不足和过剩之间的决策权衡。Tomlin[28]研究了供应商和制造商同时投资产能时的协调问题。Erkoc等[29]和Jin等[30]设计了产能预留契约来协调上游供应商的产能投资问题。当需求信息不对称时,下游制造商会夸大需求预测[31],Özer等[32]设计了非线性的产能预留契约和提前采购契约来解决该问题。在信息对称情境下,相关学者使用惩罚[33]、补偿[34-36]、收益共享[36]、成本分担[37]等契约来协调产能投资问题。在考虑提前期的两阶段模型中,供应商在第1阶段确定产能水平,零售商在第2阶段观察到需求信息后确定订货量和零售价格。Chen等[38]设计了风险和收益分享契约对其进行协调。Lu等[1]在双层供应链中考虑了产能扩张投资问题,但零售价格是外生给定的,且没有考虑促销努力和供应链协调。在两阶段生产供应链中,Huang等[39]比较了基本策略、批发价折扣和产能扩张策略3种生产策略,结果表明,当单阶段的产能不足时,产能扩张是该供应链的占优策略,但其同样没有考虑零售商的价格和促销努力决策。
上述文献表明:①现有文献大多都是在不确定需求下研究产能投资量(或备货量)问题(报童问题);②可以用不同的协约形式来协调供应链中的产能投资问题;③制造商产能扩张的研究中还未考虑产能扩张与零售商营销决策之间的交互。
在产能设定方面,邵晓峰等[35]假设制造商的生产能力调整速度很快,当供应商的生产能力出现约束时,制造商可以一个更高的采购价格从外部其他渠道获取关键零部件,从而不受产能约束。该假定与本文的产能扩张的设定类似,但也存在不同,例如在其模型中外购件的单位成本是外生给定的,而本文中产能扩张成本是边际递增的(类似研究有文献[1])。另外,本文还考虑上游企业的批发价决策以及下游企业的促销努力。在下游企业决策方面的研究有:Chen等[38]的两阶段模型的第2阶段中零售商的价格决策与本文设定类似,但其未考虑零售商的促销努力决策;常珊等[40]在报童模型下考虑了类似的产能柔性,但是没有考虑零售商的营销行为;Gurnani等[10]考虑了零售商在数量约束下的促销努力决策问题,但是在转售价格维持契约下零售商没有定价权,且没有考虑制造商产能扩张的情况。
2 基本假设与模型分析
2.1 基本假设
考虑由一个风险中立的制造商和一个风险中立的零售商组成的供应链。零售商面临着对价格p敏感且会受到促销努力e影响的市场需求q(p,e)。假设零售商的促销努力效率为γ,即单位促销努力可以带来γ单位的需求。因此,参考文献[10-11,13],需求函数可表示为

式中:a表示市场潜在需求;b>0表示市场需求对零售价格的敏感性(为简化分析,假设b=1)。同时,促销努力也会产生成本,假设促销努力成本系数为α,且边际成本递增,即单位成本的促销努力获取客户的难度越来越大。参考文献[3,15],促销努力成本可表示为αe2。为保证解的存在性和唯一性,假设γ2<4α,其潜在含义是促销效率不可能太高,否则零售商会无限制地开展促销以增加需求。假设制造商初始产能水平为K,单位产品生产成本为c,并以批发价w向零售商供货。假设制造商有如下两种可选产能策略用于满足零售商所确定的市场需求。
2.1.1 可扩张的产能策略(E) 在产能策略E 下,
当K无法满足q时,制造商可通过扩张产能的方式满足需求q。产能扩张可通过外部资源交易或内部产能转换实现。对于前者,制造商可以更高的价格从外部采购[35]或临时性委托制造,以快速调整生产能力,云制造平台将进一步促进这种产能扩张方式的发展;对于后者,智能制造工厂可以将产能在多个产品线之间进行灵活转换,从而让某个产品的生产不受现有产能水平的约束。此外,还可临时雇佣更多工人或延长设备运行时间等方式调整产能。无论采用哪种形式,额外产能的获取都需要企业付出更多的成本,即体现规模不经济性。为满足超过初始产能水平的需求,参考Lu等[1]的做法,假设产能扩张产生的额外成本为β(q-K)2/2,则总生产成本为:cq+β[(q-K)+]2/2。
2.1.2 受约束的产能策略(P) 在产能策略P下,制造商的初始产能量水平将是其可以向市场供应产品量的上限,其需要通过价格调整来匹配产能和需求,因此,可满足的市场需求为min{q,K}。相应地,产能策略P下的总生产成本为cmin{q,K}。
2.2 分散决策时各产能策略下的决策问题
制造商根据零售商所决定的市场需求进行生产,因此,通过逆序法依次求解两个企业的决策问题。在分散结构下,供应链中各主体都以自身利益最大化为原则进行决策,零售商的决策问题可以表示为(下标R 表示零售商)

给定制造商的批发价,分别求零售商利润πR(p,e)关于p和e的偏导数,并令其等于0,联立求解可得到零售商的决策及相应的需求,关于批发价w的表达式为:

制造商会依据零售商的上述决策做出自己的最优决策。对于制造商而言,有两种可选产能策略(下文中,下标M 表示制造商,E 表示可扩张的产能策略,P表示受约束的产能策略)。
2.2.1 产能策略E下制造商的决策问题 一旦制造商采用可扩张的产能策略(E),即意味着当市场需求量超过了制造商的初始产能水平时,制造商可通过产能扩张的方式以满足超过其初始产能水平的需求量。此时,制造商的决策问题为

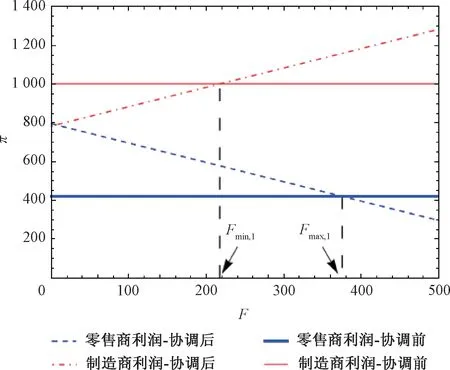
命题1在可扩张的产能策略(E)下,当K 命题2在可扩张的产能策略(E)下,当K≥K0时: 证明见附录B。 命题1和命题2表明,在初始产能水平较低状态下,可扩张的产能策略(E)的价值将得以体现,但产能扩张量会受到诸多因素的影响,例如初始产能水平K、产能扩张成本系数β和促销效率γ等。初始产能水平越高,产能扩张成本越高,则产能扩张量越少。因此,初始产能水平和产能扩张成本系数会对产能扩张量产生负向影响。较高的促销效率会带来更多市场需求,从而需要更高产能量来满足该需求。因此,促销效率对产能扩张量会产生正向影响。在产能扩张状态下,优化促销效率(γ)可以为供应链带来足额的需求增量和更高的批发价,制造商会从中获益,但零售商可能因此而利润受损。一方面,零售商会因需求量增加而获得销售增量;但另一方面,制造商会通过批发价向零售商转移产能扩张带来的成本,同时零售商还需要承担额外的促销成本。因此,当产能扩张成本系数太高时,零售商改善促销效率带来的收入不足以抵消由此增加的成本而利润受损。 管理启示:当产能不充足时,制造商可以通过扩张产能的方式来满足更多需求,但会通过批发价转移部分产能扩张成本;开展促销活动是零售商用来增加销量的常用策略,但如果零售商试图改善促销效率,则需要明确制造商的产能状态,即当制造商的产能扩张技术效率较高时,零售商改善促销效率才会对自身有利。 2.2.2 产能策略P下制造商的决策问题 在产能策略P下,制造商的产量可能会受制于其初始产能水平,即其产品生产量不会超过K。制造商的决策问题可表示为 求解上式,并结合式(3)~(5),可有如下命题。 命题3在受约束的产能策略(P)下,当K 命题4在受约束的产能策略(P)下,当K≥K0时: 证明见附录B。 上述命题表明,在受约束的产能策略(P)下,促销效率(γ)对企业决策和利润的影响与制造商初始产能水平有关。制造商产能受限时,改善促销效率会导致更高的零售价格和促销努力水平,制造商也会依此设定更高的批发价。虽然零售价格的提升会增加零售商的销售收入,但是更高的促销努力水平会产生更高的促销成本,同时也要面临更高的批发价,这些都将侵蚀零售商的利润,并最终使零售商遭受利润受损。制造商产能充足时,零售商通过改善促销效率带来的需求增量,都能被制造商充足的产能所满足,而无需利用批发价对其进行调节。因此,在量价齐升的情况下,零售商可以从促销效率改善中获益。制造商作为供应链的主导者,总可以从促销效率提升中获益:在产能不足时,其可以通过提高批发价获益;在产能充足时,其可以通过满足更多市场需求而获益。 管理启示:当制造商不具备产能扩张能力时,零售商应谨慎选择是否改善其促销效率。特别是当制造商产能不充足时,促销效率的改善可能使零售商面临更高的批发价,从而使自身利润受损。对于制造商而言,在不同产能状态下可以有不同的实现利润最大化的方式。 假设存在一个集中决策者,其同时决策产品的零售价格p和促销努力e。在两种产能策略下,集中决策者将有不同的决策问题(上标I表示集中结构)。 2.3.1 可扩张的产能策略(E)下的最优决策及利润 集中决策结构下,采用产能扩张策略,即意味着市场需求高于供应链系统初始产能水平时,集中决策者可以采用产能扩张的方式满足超出初始产能水平的需求。此时,集中决策者的优化问题为 对上述问题的求解可得如下命题。 命题5可扩张的产能策略下,当K<2K0时,集中决策者的最优决策和利润为: 命题6可扩张的产能策略下,当K≥2K0时,集中决策者的最优决策和利润为: 证明见附录B。 命题5和命题6呈现了集中系统在可扩张产能策略下的决策和利润。与分散结构下的初始产能水平边界(K0)相比,集中结构下可扩张的产能策略(E)发挥作用时初始产能水平有着更宽的边界(2K0),这意味着集中系统可以达到更高的最优产出量。 2.3.2 受约束的产能策略(P)下的最优决策及利润 当无法进行产能扩张时,集中决策者只能通过价格和促销努力决策实现自身利润最大化,集中系统的利润函数可表示为 对上述问题的求解可得如下命题。 命题7受约束的产能策略下,当K<2K0时,集中决策者的最优决策和利润为: 命题8受约束的产能策略下,当K≥2K0时,集中决策者的最优决策和利润为: 证明见附录B。 命题7和命题8呈现了集中系统在受约束的产能策略下的决策和利润。同样地,与分散结构下的初始产能水平边界相比,集中结构下也具有更宽的边界,从而可达到更高的最优产出量。 本部分将在分散结构和集中结构下,对两种产能策略下的决策和利润进行比较,并探讨不同因素(K、α或γ)的影响。 命题9在可扩张的产能策略(E)和受约束的产能策略(P)下,制造商和零售商的决策及利润满足如下关系(其中,0 <γ2<4α,K0=α(a -c)/(4α-γ2)): 证明见附录B。 命题9 表明,当初始产能水平足够高(K≥K0)时,两种产能策略下的决策问题均等价于无产能约束下的决策问题,从而具有相同的决策和利润,这比较符合直观;但当K 管理启示:采用可扩张的产能策略可以为供应链带来更高的产能柔性,对供应链成员都有利。但在进行产能扩张时,如果促销努力效率偏低,零售商应向市场提供数量更多但价格更低的产品;如果促销效率偏高,则零售商应高价销售产品。 命题10在可扩张的产能策略和受约束的产能策略下,集中结构下的利润大小满足如下关系:当K<2K0时,;当K≥2K0时, 证明见附录B。 命题10表明,在初始产能水平不超过2K0时,与受约束的产能策略相比,可扩张的产能策略下集中决策者可以获得更高利润。因此,可扩张的产能策略应作为该供应链系统的首选。此策略下的系统利润是该系统可以实现的最优利润,将作为后续设计协调契约的标杆。 命题11在可扩张的产能策略(E)下,分散决策结构和集中决策结构下产量和利润满足如下关系: 证明见附录B。 命题11表明,在分散结构下由于双重边际效应的存在,零售商和制造商都以自身利益最大化为目标进行决策,从而导致供应链中的产量和总利润要低于集中决策结构下的产量和利润。因此,下文将通过设计协调契约,使零售商和制造商在分散结构下也能实现集中结构下的生产数量和利润,且都获得更高的利润,实现整个系统利润的Pareto改进。 命题10表明,可扩展的产能策略(E)对于整个系统而言是一种优势策略;而命题11表明,分散结构下的企业决策会导致供应链系统的低效率,从而无法充分发挥产能扩张和促销努力的效果。下文将设计适用的契约对供应链成员的决策进行协调,以实现整个供应链系统绩效的改善。由于为消除制造商与零售商之间的双重边际效应,增加分散决策下的生产量,下文将利用理论和实践中常用的两部定价契约(w,F)进行协调。其中,w为零售商从制造商处采购所支付的批发价,F为零售商与制造商之间的转移支付。为简化表示,用和分别表示在产能策略E 下使用两部定价契约时零售商和制造商的利润,其他符号含义同前文, 求解上述问题,可有命题12。 命题12两部定价契约(w,F)可以协调产能策略E下的供应链,但需满足: (1)当0 如果0 (2)当K≥2K0时,wF=c,Fmin,3≤F≤Fmax,3。 其 中,Fmin,1、Fmax,1、Fmin,2、Fmax,2、Fmin,3、Fmax,3表达式见附录证明。 证明见附录B。 命题12表明,在可扩张的产能策略下,使用两部定价契约可以协调该供应链,但契约中的参数(批发价和转移支付)应根据制造商初始产能水平的状态进行调整。 为直观地分析本文所得相关结论,并进一步揭示相关参数对企业决策及利润的影响,本节利用数值仿真方法进行分析。在满足约束条件α>γ2/4的前提下,取如下参数值:a=100,c=30,α=2.5,γ=2,β=2。 (1)不同产能策略下的最优生产量。在上述参数值设定下,初始产能水平不同可能会使供应链确定不同的最优生产量。在分散结构下,当K 图1 不同产能策略下初始产能水平K 对最优生产量的影响 (2)不同产能策略和决策结构下的企业(供应链)利润。图2(a)~图2(c)表明,当K 图2 不同产能策略和决策结构下的利润 (3)协调契约参数对企业利润的影响。两部定价契约(w,F)可以协调考虑促销努力和产能扩张的供应链,但需要设置合适的参数值以适应制造商不同初始产能水平带来的影响。给定制造商初始产能水平,则可以确定实现供应链协调的批发价,以及确保制造商和零售商都受益的转移支付范围。例如,当K=23.3 图3 当K=23.3时可实现供应链协调的F 取值范围 (4)初始产能水平对契约协调参数上界和下界的影响。图3展示了特定初始产能水平下,实现供应链协调的转移支付边界。图4则从更一般的角度展示了不同初始产能水平对应的转移支付边界。当K≤2K0时,随着制造商初始产能水平的提高,整个供应链利润递增(见图2(c)),且零售商利润增速更快(见图2(a)和图2(b));同时,为实现供应链协调,制造商需要接受更低的批发价,以消除双重边际效应。因此,零售商需要向制造商转移更多的利润,才能确保协调后的制造商利润有所改善,即Fmin和Fmax均会随着K递增(见图4)。 图4 不同K 值下实现供应链协调的F 上界和下界 有效的产能管理不仅能够提高企业运作效率,还可以改善其供应链绩效。本文在双层供应链结构下研究了考虑零售商促销努力的制造商产能策略及协调机制。研究结论表明: (1)初始产能水平不足会促使供应链选择产能扩张,该策略的实施会使制造商和零售商都从中获益。在产能扩张状态下,零售商应谨慎地改善其促销效率,因为当产能扩张成本系数偏高时,制造商会通过批发价向零售商转移成本,从而使零售商利益受损。 (2)在可扩张的产能策略下,两部定价契约可以实现供应链协调,但批发价和转移支付应根据制造商的初始产能水平状态进行设定。 本文仅考虑了风险中立的制造商和零售商之间的博弈决策问题,由于产能投资也存在一定风险,将制造商的风险态度纳入模型中将是一个非常有意义的方向。此外,也可在竞争因素、不确定性、权力结构差异等方面做进一步拓展。 附录A 附表1 分散结构下各企业的均衡决策及利润 附表2 集中结构下的最优决策及利润 附录B 命题1和命题2的证明零售商的利润表达式为:πR(p,e)=(p-w)q-αe2,分别求其对p和e的偏导数,并令其等于0,可有: 当γ2/α<4时,上述矩阵是负定的,即πR(p,e)是p和e的凹函数。通过式(B1)和(B2)可求得:p(w)=w +代入式(1),可有,即分别对应正文中式(3)~(5)。 (1)当K 制造商利润关于w的二阶导数,当4α-γ2>0或4α-γ2+αβ<0时,,即πM,E(w|K)是关于w的凹函数。通过求解式(B3)可得:分别代入式(3)~(5),可得: 进而可得零售商和制造商利润,分别为: 由前文假设K 产能扩张量 (2)当产能充足即K≥q(w)时,πM,E(w|K)=(w-c)q(w),将式(5)代入,并令其关于w的一阶导数等于0,可有: 求解式(B4)可得(a+c)/2,分别代入正文中式(3)~(5),可得: 由前文假设K≥q(w)可有,即当K≥K0时可得上述均衡决策。将其汇总于附录A 中附表1。 在此情景下,产能充足K≥K0,即产能扩张量命题2得证。 命题3和命题4的证明在产能策略P下,制造商利润函数为:πM,P(w|K)=(w-c)min{q(w),K}。假设在无产能约束下的均衡批发价为w*。 (1)当K≥q(w*),即制造商产能较充足时,πM,P(w|K)=(w-c)q(w),最优批发价的求解方法同前文产能策略E中在无产能约束下对最优批发价的求解。相应地,均衡决策表达式为: 制造商产能充足意味着K>K0。将上述各式汇总于附录A 中附表1。 (2)若K 将上述结果汇总于附录A 中附表1。 命题5和命题6的证明在产能策略E下,集中系统的利润为:,且由式(1)可知q=q(p,e)=a-bp+γe。 (1)当K足够大时,集中决策者不会受到初始产能的约束,此时集中系统的利润为:πIE(p,e)=(p-c)q(p,e)-αe2,分别求利润关于p和e的偏导数并令其等于0,可有: (2)当K不充足(即K<2K0)时,集中决策者会受到初始产能水平的约束,此时集中系统的利润可以表示为: 分别求其关于p和e的偏导数并令其等于0,可有: 联合上述两式并求解可有: 将零售价格和促销努力分别代入需求函数和利润函数,可有: 将上述结果汇总于附录A 中附表2。命题6得证。 命题7和命题8的证明在产能策略P下,集中结构利润为:(p,e)=(p-c)min{q(p,e),K}-αe2,同前文分析思路,下文将考虑两种情景下的决策问题。 (1)当K足够大,即无产能约束时(p,e)=(p-c)q(p,e)-αe2。此时,最优决策问题与产能策略E下的决策问题相同,因此,可直接得到相应决策及利润,分别为:且K≥2K0。 (2)当初始产能水平不足,即受产能约束(K<2K0)时,供应链会充分利用产能,即(p,e)=(p-c)K-αe2。即供应链会提高产品价格p或降低促销努力e,使市场需求恰好满足q(p,e)=K,以实现系统利润最大化,即 将式(B5)代入利润式,可有(e)=(p(e)-c)K-αe2。求该利润关于e的导数,并令其等于0,可有Kγ=0,可得将其代入式(B5),可有。相应地,可有:,其中,K<2K0。 将上述结果汇总于附录A 中附表2。命题7和命题8得证。 命题9的证明下文将以附录A 中附表1为基础对命题9进行证明。 (1)当K (2)当K≥K0时,由附表1易知产能策略E、P下的各决策与利润表达式是相同的,因此,命题9(2)直接得证。 命题10的证明附录A 中的附表2呈现了两种产能策略下集中系统的决策和利润。 (1)当K<2K0时,产能策略P、E下的利润作差可有 (2)当K≥2K0时,由附表2中的表达式可直接得到命题10得证。 命题11的证明根据附录A 中的附表1和附表2,下面将分3个阶段依次比较产能策略E 下分散决策和集中决策下的生产量和总利润。 (1)当K (2)当K0≤K<2K0时, 命题12的证明在两部定价契约(w,F)下,w为零售商从制造商处采购所支付的批发价,F为零售商与制造商之间的转移支付。两部定价契约(w,F)能协调供应链需要满足两个条件:①实现与集中结构下相同的决策;②供应链中各成员的利润情况会更好(至少不会变差)。在两部定价契约下零售商和制造商的利润分别为: 根据决策顺序,首先计算零售商的价格和促销努力决策,然后再进行制造商的批发价决策。 分别求式(B6)关于p和e的偏导数,并令其等于0,可有: 同附录中命题1的证明,当γ2<4α时,可求得: (1)当K<2K0时,集中系统因初始产能不足而处于产能扩张状态,且此时的产量为:。为实现产量上的协调,需满足,即w应设定为 将其代入式(B8)和(B9),并对比附表2中表达式,可有: 可知在K<2K0的情况下,两部定价契约实现了与集中结构下相同的决策,同时还实现了系统最优利润。 (2)当K≥2K0时,集中系统处于产能充足状态,且此时同上,为实现产量上的协调,即qF(w),应将w设定为 同上,将其分别代入式(B8)和(B9)并与附表2中表达式对比,可有: 因此,同样地,当K≥2K0时,两部定价契约也可以实现与集中结构下相同的决策,且实现系统最优利润。 上述结论表明,两部定价契约满足了协调契约的第1个条件,协调契约的第2个条件应满足 (1)当K 即在两部定价契约下,当K (2)当K0≤K<2K0时, 即在两部定价契约下,当K0≤K<2K0时,如果,且Fmin,2≤F≤Fmax,2,则零售商和制造商的利润都会得到改善。 (3)当K≥2K0时, 即在两部定价契约下,当K≥2K0时,如果wF=c,且Fmin,3≤F≤Fmax,3,则零售商和制造商的利润都会得到改善。 综上可有: (1)当K<2K0时,,如果0 (2)当K≥2K0时,wF=c,Fmin,3≤F≤Fmax,3。其中: 命题12得证。

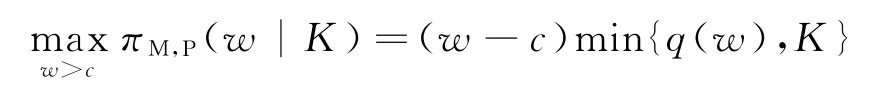

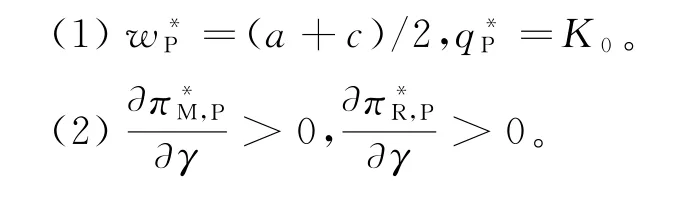
2.3 集中决策时各产能策略下的决策问题
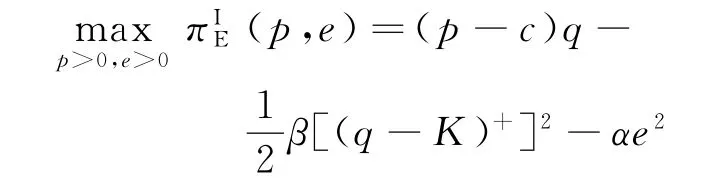


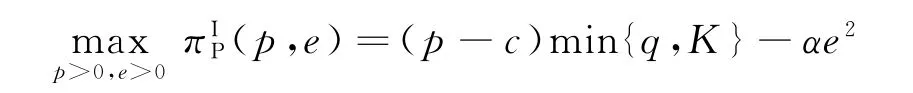

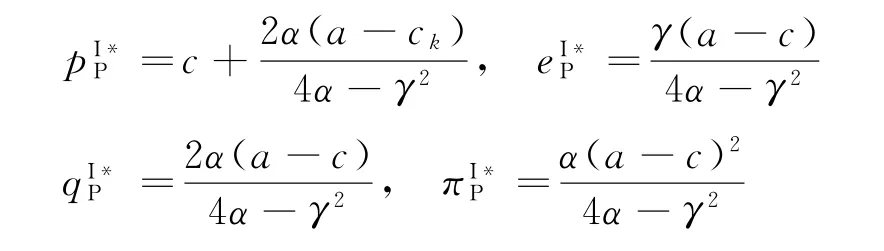
3 不同产能策略下的决策及利润的比较分析

4 供应链协调分析

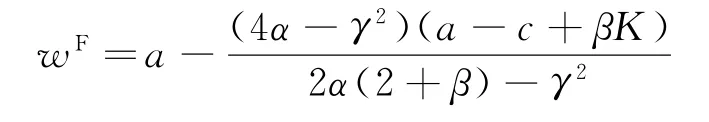
5 数值分析



6 结论