CZ铁路色季拉山隧道高地应力岩爆风险定量预测研究*
2022-08-02田朝阳兰恒星许博闻
田朝阳 兰恒星② 张 宁 许博闻
(①长安大学地质工程与测绘学院, 西安 710054, 中国)
(②中国科学院地理科学与资源研究所, 资源与环境信息系统国家重点实验室, 北京 100101, 中国)
0 引 言
CZ铁路是我国藏区综合交通运输体系的重要组成部分,对维护我国国家长治久安、促进西藏自治区经济社会发展具有重大意义(彭建兵等, 2020)。CZ铁路沿线地貌陡峻,内外地质作用异常活跃,多场环境耦合作用强烈,地质环境条件极其复杂。全线桥隧占比超过80%,存在多条特长深埋隧道,在极端复杂的工程环境及强烈的工程扰动影响下,这些深埋长隧建设过程中工程灾害问题更加凸显(郭长宝等, 2017; 薛翊国等, 2020; 赵勇等, 2021)。其中:色季拉山隧道位于西藏自治区林芝市境内,全长37.965km,最大埋深1696m,为新建CZ铁路雅安林芝段先期开工隧道和全线重点控制性工程。隧道地处青藏高原东南缘的喜马拉雅东构造节附近,属于印度洋板块向欧亚板块俯冲、楔入的最前缘,是现今全球构造活动最为剧烈的地区之一(常利军等, 2015; 兰恒星等, 2021)。强烈构造背景下形成的构造应力和深埋应力耦合成的高地应力特征,加之隧道沿线高度发育花岗岩、闪长岩和片麻岩等硬质岩,使得色季拉山隧道在建设过程中,将面临着严重的高地应力岩爆问题。
岩爆是在工程开挖过程中,围岩发生应力释放而产生脆性破坏的一种岩体失稳过程,具有突发性、高危害性等特点,是高地应力地区地下隧道建设过程中所面对的主要风险之一(靳晓光等, 2013; 蒋钰峰等,2019)。岩爆的发生取决于两个条件:一是岩体能够储存大量能量,同时在破坏过程中表现出强烈的弹射倾向; 二是岩体所在区域存在形成较高的应力集中的地应力环境(王开洋等, 2014; Pan et al.,2021)。
准确的预测预判岩爆发生的位置以及强烈程度对高地应力区域地下工程的修建具有重要指导意义,也是岩爆研究中的热点和难点问题。Neyma于1972年提出了能够反映岩石弹性变形能储存能力的岩爆倾向性指数Wet(Homand et al.,1990),其后诸多学者采用此指标进行岩爆倾向性评估,并根据不同的适用条件、提出了相应的岩爆倾向性评价标准(Kidybinski, 1981; Singh, 1988)。然而,除了围岩的自身性质之外,岩爆的发生还取决于围岩所处区域的地应力环境(李鹏翔等, 2019)。Barton(1974)研究挪威隧道围岩稳定性过程中发现,岩石单轴抗压强度与最大主应力的比值与岩爆之间具有一定的关系,并根据强度应力比指标划分了相应的岩爆等级分级标准。此后,国内外学者根据工程实践经验以及理论推导,先后提出了Russense判据(Russense,1974)、Hoek判据(Hoek et al., 1980)、陶振宇判据(张镜剑等, 2008)、二郎山判据(徐林生等, 1999)、国标法(中华人民共和国国家标准编写组,2008)等一系列应力指标型(应力与强度或者强度与应力的比值)岩爆判据。随着新技术理论的发展,以及对岩爆问题探索的深入,涌现了一批如模糊综合预测、BP神经网络预测、声发射现场检测预报等新的岩爆预测方法与理论(李庶林, 2009; 陈鹏宇等, 2014; Roohollah et al.,2019)。
上述方法中,应力指标判据法同时考虑了岩爆发生的两大条件:围岩自身性质以及外部地应力条件,并分别将其用地应力量值、岩石强度这两个相对易获取的指标参数进行表征。在实际应用中,通过有限的实测地应力数据进行反演,结合地质资料中岩石的强度参数,即可方便快捷地得到隧道的岩爆预测结果,是目前应用最广泛的岩爆预测方法。然而,现有强度应力判据采用岩石强度参数多通过完整岩块的室内试验获取,忽视了原位岩体强度的结构损伤效应。此外,这些判据多为岩爆等级的定性预测,难以给出岩爆的范围和程度的定量预测。而量化研究岩爆对于硐室围岩的破坏程度和影响深度,对于选取恰当的加固方式以及支护参数,预防并降低岩爆对于隧道建设的不利影响、确保工程的顺利开展具有重要意义。
为此,本文收集了大量国内外典型岩爆隧道的特征参数并进行统计分析,建立了一种通过应力强度比来预测岩爆爆坑深度的岩爆定量化预测模型。同时,通过室内力学试验和岩体强度损伤理论获取了隧道沿线岩体强度参数,以多元线性回归法反演了隧道沿线地应力参数,最终对CZ铁路色季拉山隧道的岩爆风险进行了定量化预测和分析,并与同属雅鲁藏布缝合带影响区、地质条件相近的已贯通CZ铁路巴玉隧道岩爆风险进行了对比评价,成果可以为色季拉山隧道施工与岩爆风险防控提供重要参考。
1 岩爆定量化预测模型与岩体强度损伤准则
1.1 脆性破坏定量化预测模型
岩爆是多种因素共同耦合的结果,其中应力和围岩性质(主要包括强度和完整性)是导致脆性破坏发生的最显著的两个条件(Martin et al.,1994)。对于裂隙网络不发育的完整岩体,当应力强度比较高时,开挖界面附近的岩体发生应力集中而产生脆性破坏,且隧道围岩的破坏深度随着应力强度比的增加而逐渐增加,即硐室的破坏深度与其应力强度比之间具有一定的函数关系(Martin et al.,1999)。基于这一发现,Martin et al. (1999)根据实测数据对应力强度比和硐室围岩的破坏深度进行了拟合(图1),建立了应力强度比与硐室破坏深度的关系表达式:

图1 硐室围岩破坏深度与最大切应力关系图(Martin et al., 1999)Fig. 1 Relationship between depth of failure and the maximum tangential stress at the boundary of the opening
(1)
式中:Df为硐室破坏影响深度,等于隧道破坏深度与隧道半径的和;a为隧道半径;σc为完整岩石的单轴抗压强度;σmax=3σ1-σ3,为硐室围岩的最大切向应力,其中,σ1为最大主应力,σ3为最小主应力。
由图1可以看出,硐室围岩破坏深度与最大切向应力之间具有良好的线性关系,通过式(1)反算,得到围岩发生脆性破坏的临界应力为0.4σc(Df/a=1)。该方法针对应力引起的完整或少量微裂隙的脆性围岩破坏建立,将传统的应力强度比与围岩破坏深度联系起来,可以实现量化预测应力集中下的围岩脆性破坏深度。
1.2 岩爆定量化预测模型
基于上述思路,通过收集66个典型岩爆隧道的实例数据,对包括乌兹别克斯坦甘姆奇克隧道、二郎山隧道、锦屏二级水电站引水隧洞、拉林铁路桑珠岭隧道、花瓶山隧道等典型岩爆隧道的岩性、地应力、抗压强度、隧道跨度以及最大爆坑深度等参数进行了统计。典型岩爆隧道参数统计见表1。

表1 典型岩爆隧道统计Table 1 Statistics of typical rockburst tunnels
表中σ1为最大主应力;σ3为最小主应力;σc为岩石单轴抗压强度
对收集的岩爆隧道的应力强度比以及爆坑深度数据分析发现,应力强度比与隧道岩爆的爆坑深度具有良好的线性关系。通过建立隧道岩爆爆坑深度与应力强度比之间的关系,对收集的66组数据进行回归分析,得到拟合公式:
(2)
拟合关系曲线如图2所示。可以看出,爆坑影响深度Df与应力强度比σmax/σc之间具有良好的线性关系,同时,由式(2)推导出的岩爆起始应力为0.32σc(Df/a=1),与Martin et al. (1999)提出的临界脆性破裂应力范围0.4σc接近。

图2 岩爆量化预测模型Fig. 2 A universal quantitative rockburst prediction model
Hoek et al. (1980)根据南非金矿工程经验,提出采用围岩切向应力与岩石单轴抗压强度比值σmax/σc来对岩爆进行评价并给出了岩爆等级划分界限以及相应的支护建议,其后得到广泛的应用。因此,综合隧道爆坑深度和Hoek et al. (1980)提出的岩爆等级划分依据,确定出本文预测模型中岩爆等级划分依据如表2所示。

表2 岩爆等级分级标准Table 2 Classification of rockburst grades
本文建立预测模型所用参数包括岩石的单轴抗压强度,最大切向应力和爆坑影响深度等参数。最大切向应力反映了对隧道围岩脆性破坏发生起重要作用的原位应力状态,而采用爆坑影响深度,很好地考虑到岩爆对于整个隧道围岩破坏程度的量化值。因此,基于该预测模型,通过室内试验获得完整岩石的单轴抗压强度,并结合现场原位地应力测试,即可实现岩爆风险的定量化预测。
1.3 结构岩体强度损伤准则
Hoek et al. (2002)考虑到受结构裂隙、风化以及开挖过程中的工程扰动等因素的影响,岩体的强度相比于实验室测得的岩块强度将有大幅度的下降,并根据完整岩石的物理学试验和裂隙岩体的模型研究结果,建立了一种考虑结构损伤效应的岩体强度估算理论。该方法的原理为:通过引入相关折减系数,对完整岩石的基本物理参数和力学参数进行折减,以获取含结构裂隙岩体的强度参数。该理论目前是较为完善的岩体强度估算方法之一(谢和平等, 2022),在对岩体强度进行合理估计的同时,大大节约了岩体强度测试的成本和不方便性,在实际工程中得到广泛的应用。其最新修正表达式为(Hoek et al.,2019):
(3)
式中:σ1、σ3分别为岩体破坏时的最大、最小主应力; σc为完整岩石单轴抗压强度;mb为岩石材料常数mi(范围: 0.0000001~25)的折减系数,可根据式(4)确定;
(4)
式中:s和α为岩体常数,可分别由式(5)和式(6)确定:
(5)
(6)
式(4)~式(6)中:GSI为岩石的地质强度指标;D为扰动常数,反映岩体受开挖、爆破等外界因素所影响的程度,介于0~1之间。
在开挖过程中,靠近隧道边界的岩体处于临空状态,因此可认为σ3=0,此时岩体的强度可由式(3)简化为:
σcm=σcisα
(7)
式中:σcm为岩体强度。
对于质量控制良好的隧道掘进机开挖等方式,其对隧道围岩的扰动可以控制在较小的水平,D可取值为0(Hoek et al.,2019)。此时,地质强度指标GSI的大小将直接决定结构岩体强度损伤的程度,即可根据室内完整岩块强度参数和GSI指标求取原位岩体强度。
2 工程实例应用
2.1 工程概况及工程地质条件


图3 色季拉山隧道地质纵断面Fig. 3 Geological profile of Sejila Tunnel

表3 色季拉山隧道围岩等级统计Table 3 Statistics of surrounding rock grade of Sejila Tunnel
2.2 工程区岩石力学性质
将工程区取回的钻孔岩芯加工成标准样,分别进行单轴抗压强度试验和巴西劈裂实验,得到工程区岩石力学参数统计结果见表4。可以看出,隧址区岩石抗压强度较高,一般大于100MPa。岩石自身是否具有发生岩爆的本质属性,通常以岩爆倾向性指标进行评价。目前,反映岩石硬脆程度的脆性系数B,是目前应用最简便、广泛的岩爆性倾向指标之一(王开洋等, 2014),其计算公式为:

表4 隧道岩石基本力学参数Table 4 Statistics of basic mechanical parameters of rock of Sejila Tunnel
B=σc/σt
(8)
式中:σt为岩石的抗压强度。
根据式(8)以及岩石强度参数测试结果,计算得到隧址区花岗岩、闪长岩以及片麻岩的脆性系数B分别为20.07、21.56以及16。徐林生等(1999)提出脆性系数B判断岩爆倾向性的界限:B≥18时,强烈岩爆; 18>B≥14,中等岩爆; 14>B≥10,轻微岩爆; 10>B无岩爆。因此,由式(8)可判断出,除片麻岩为中等岩爆倾向外,闪长岩和花岗岩均具有强烈岩爆倾向性。
隧址区岩体以弱风化为主,岩体完整性总体较好,以完整、较完整岩体为主,揭露岩芯柱可长达0.5~1m,部分段落存在断层破碎带及节理密集带。基于室内岩石物理力学试验参数、野外钻孔岩芯描述、工程物探及初步岩体分级等资料,采用定性与定量相结合的方法确定出隧道沿线岩体质量指标GSI分布范围,如图4所示。利用前述Hoek-Brown岩体强度损伤准则及软件RocLab对隧道轴线岩体强度参数进行分析估算,如表5所示。
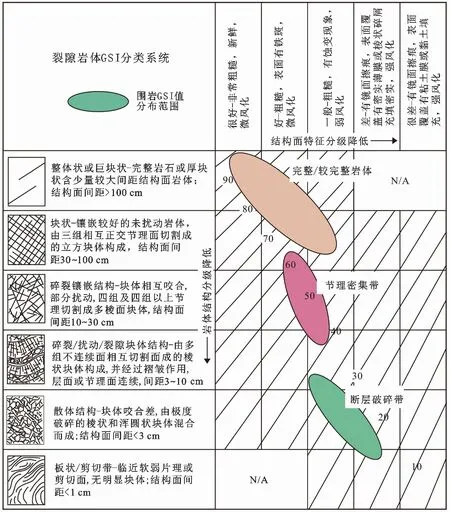
图4 隧道沿线岩体质量GSI分布范围Fig. 4 Distribution of GSI along the tunnel

表5 利用Hoek-Brown强度准则估算隧道轴线岩体强度Table 5 Strength of rock mass around tunnel section based on Hoek-Brown Criterion
2.3 隧址地应力特征
隧址区位于喜马拉雅东构造结附近,区域内新生代以来地壳急剧抬升、板块强烈挤压,造成了地应力高且主应力方向复杂的初始地应力场特征。在前期勘察过程中,沿隧道沿线共布置地应力测量孔10个,采用水压致裂法对代表性测段进行测试,为了减小山坡卸荷和沟谷应力集中等干扰因素,测段深度一般超过100m,最大孔深达1450m(张玉玺, 2021)。地应力测试结果见表6。

表6 隧址区地应力测量结果Table 6 In situ stress measurement results

为进一步分析隧址区地应力状态,根据水力压裂测试结果分别计算出隧址区地应力特征参数Kav、KHv和Khv,其表达式如下:
Kav=(SH+Sh)/2Sv
(9)
KHv=SH/Sv
(10)
Khv=Sh/Sv
(11)
式中:Kav为侧压力系数;KHv为最大水平应力系数;Khv为最小水平应力系数; 可以反映水平应力相对于垂向自重应力的关系。
隧址区地应力特征参数随深度变化的规律如图5所示。可以看出,色季拉山隧道地应力特征参数分布特征表现出相似的趋势,可通过双曲线进行拟合。在埋深较浅的近地表附近,各地应力特征参数基本大于1,三向主应力之间关系为SH>Sh>Sv,此时,反映出隧址区受水平构造作用影响较大。同时,由于受地形切割、卸荷以及风化剥蚀等作用的影响,浅部地应力特征参数离散程度较大。随着深度增大,隧道地应力特征参数及其波动范围逐渐减小。在埋深大于500m之后,Kav趋于1.14±0.2,KHv趋于1.36±0.26,Khv趋于0.97±0.19,三向主应力之间关系逐渐转变为SH>Sv>Sh,隧址区的应力场仍表现为以水平应力为主的构造控制作用,但自重应力的影响显著加强。

图5 色季拉山隧道地应力特征参数Fig. 5 Characteristic parameters of in-situ stress of the Sejila Tunnela. 侧压力系数Kav; b. 最大水平应力系数KHv; c. 最小水平应力系数Khv
2.4 初始地应力场反演分析
地应力是隧道工程围岩发生变形破坏的关键性因素和重要工程荷载来源,直接影响隧道工程的施工安全(李天斌等, 2019)。由于场地、经费等诸多因素的影响,难以做到对隧道全线地应力进行水力压裂测试(黄艺丹等, 2021)。因此,结合实地工程地质条件及地应力测试数据,进行地应力数值模拟与反演,对于获取分析隧址区及隧道沿线初始地应力场具有重要意义。目前常用的地应力场反演分析方法包括多元线性回归分析法、边界荷载调整法、应力函数法等(王金安等, 2015; 李天斌等, 2016; 王庆武等, 2018)。其中:多元线性回归法地应力场反演概念清晰,在许多工程中已得到了成功的应用和推广(裴启涛等, 2012)。因此,本文采用多元线性回归法进行地应力反演。
在Rhino中建立三维数值计算模型并剖分地层,模型构建过程中,采用250m薄层来模拟断层破碎带及其影响带。模型范围如下:以隧道为中心区域,垂直于隧道走向为x轴,长42km; 以隧道走向为y轴, 16km; 竖直向上为z轴,模型基底以隧道出口点高程为基准向下延伸2000m。
结合研究区的工程条件,本文选取自重应力状态、南北向水平挤压构造运动、东西向水平挤压构造运动、水平面内均匀剪切构造运动等4个因素作为回归岩体初始应力场的基本要素,回归初始地应力场表达式为:
σ地=b1σ构1+b2σ构2+b3σ构3+b4σ自4
(12)
式中:σ构1、σ构2分别为x、y方向施加的均匀挤压应力;σ构3为xy方向施加的均匀应力;σ自4为自重应力,b1~b4为回归系数。
将模型导入FLAC3D软件中进行计算。模型所使用的隧址区岩体物理力学参数综合现场地质勘察资料、室内试验结果以及Hoek-Brown经验公式(Hoek et al.,2002)确定,如表7所示。采用弹性本构模型对隧址区地应力进行反演,以ZK6钻孔实测地应力值为回归目标值,分别对式(12)确定的4种工况进行模拟计算,求解回归方程。分别得到隧址区回归系数b1、b2、b3、b4为1.89、0.14、1.05、0.45。
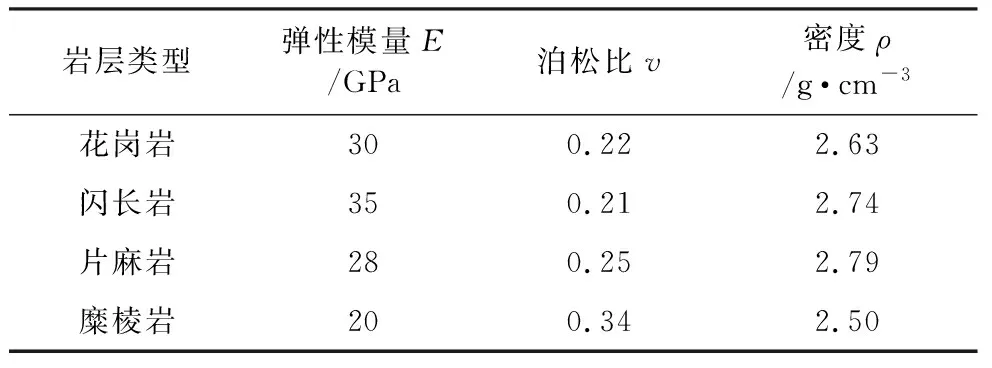
表7 隧址区岩体力学参数Table 7 Mechanical parameters of rock mass
经过应力场平衡计算,得到隧址区最大水平主应力云图如图6所示,可以看出,隧址区核心部最大主应力明显大于隧道进出口段。

图6 隧址区最大主应力云图Fig. 6 Maximum horizontal principal stress at tunnel site
考虑到靠近地表地应力实测数据较离散,因此,选取ZK6埋深大于400m的地应力实测数据与地应力场反演结果进行对比,如图7所示。可以看出,地应力回归数据与钻孔实测地应力数据比较接近,且两者随深度的变化具有较好的一致性。各测点实测值与回归模拟值相对误差计算结果见表8。可以看出,地应力回归模拟值与实测值的误差基本控制在10%以内,表现出较高的准确率。

图7 地应力实测与回归值对比Fig. 7 Comparison between measured and simulated results of Sejila Tunnel

表8 地应力回归值误差Table 8 Comparison between measured and simulated results of Sejila Tunnel
数值模拟得到的色季拉山隧道沿线地应力分布如图8所示。可以看出隧道沿线最大水平主应力为6.53~51.24MPa,最小水平主应力为4.8~36.12MPa,垂向主应力为2.26~43.62MPa。全线最大水平主应力量值水平较高,在断层带附近有明显下降。在浅埋深段水平主应力大于铅垂应力,三向主应力关系为SH>Sh>Sv,表现出明显的构造应力为主,当埋深超过500m,垂向应力大于最小水平主应力,三向主应力关系转变为SH>Sv>Sh。

图8 色季拉山隧道沿线地应力Fig. 8 Principal stress value of Sejila Tunnel
2.5 色季拉山隧道岩爆量化预测
根据色季拉山隧道沿线岩体抗压强度估算结果和地应力反演得到的隧道轴线地应力参数,采用式(2)对色季拉山隧道岩爆风险进行量化预测。为此,首先需要进行隧道最大切向应力的计算。色季拉山隧道开挖断面可近似于圆形,故可将隧道横截面假定为平面应变模型(张重远等, 2022),此时,隧道截面方向受到水平向正应力σn和上覆岩石自重作用引起的垂向应力σv,根据线弹性公式,水平向正应力计算公式为:
(13)
式中:θ为最大水平主应力SH与隧道轴向法线的夹角,根据水力压裂测试结果,色季拉山隧道θ为64°。最终,可以得到色季拉山隧道最大切向应力计算公式:
(14)
对于断层破碎带等不具备弹性应变储存条件的岩体强烈破碎区域,在较高的应力下可能发生大变形而非岩爆,因此在预测及统计隧道沿线岩爆时对该段落进行去除。最终计算得到色季拉山隧道沿线岩爆预测结果如图9所示。

图9 色季拉山隧道最大爆坑深度预测结果Fig. 9 Prediction results of maximum explosion pit depth of Sejila Tunnel
可以看出,除断层影响地带和埋深较浅的沟谷、进出口地带,隧道沿线均可能有不同程度的岩爆出现。其中:在埋深较大的地段,花岗岩、闪长岩地层将出现强烈等级程度的岩爆,片麻岩地层中将有中等程度岩爆发生。
同时对沿线岩爆段落进行统计,得到色季拉山隧道岩爆评价结果,如表9所示。可以看出,发生岩爆的段落普遍具有较高的地应力,最大水平主应力SH普遍高于20MPa,部分段落地应力可达40MPa以上,有强烈等级的岩爆发生。对不同等级岩爆段落长度进行统计,结果显示,色季拉山隧道预测岩爆段落达23254m,占隧道全长的61.25%,其中:中等岩爆段落达12188m,占隧道全长32.1%,强烈等级岩爆段落达3502m,占隧道全长的9.23%。预测隧道爆坑最大深度比Df/a可达1.67(1.46+0.21),按色季拉山隧道当量半径5.1m计算,预测最大爆坑深度可达3.42m。

表9 色季拉山隧道岩爆评价结果Table 9 Statistical chart of rockburst prediction results
2.6 色季拉山岩爆风险可控性分析
为评估色季拉山隧道岩爆风险的可控性,选取已成功贯通的CZ铁路拉林段巴玉隧道进行相似工程案例风险的定量对比分析。工程地质类比法属于定性评价的一种,它的实质是将已有的隧道风险进行总结归纳后,应用到地质条件相似的隧道风险的评价研究中,是一种应用广泛的经验方法(张宁等, 2022)。
巴玉隧道位于桑日至加查下游段,与色季拉山隧道同属于雅鲁藏布缝合带影响区,隧道全长13.047km,最大埋深约2073m。巴玉隧道岩爆问题极为突出,据13047m正洞和8131m平导的统计结果显示,隧道岩爆里程段高达94%(严健等, 2019)。
表10分别列出了两座隧道的基本概况和基本地质条件,同时也分别给出了巴玉隧道实测最大爆坑深度和色季拉山隧道预测最大爆坑深度。可以看出,两座隧道具有极其相似的工程地质条件,两座隧道地层岩性均以花岗岩为主,且岩石强度较为接近。此外,色季拉山隧道最大主应力为51.24MPa,略大于巴玉隧道最大主应力45.77MPa。根据预测结果,色季拉山隧道岩爆的最大爆坑深度可达3.42m,略小于巴玉隧道实测最大爆坑深度3.5m,同时,色季拉山隧道预测岩爆里程段占比为61.25%,远小于巴玉隧道实际岩爆段占比94%。因此,可以认为,在合理的工程措施下,色季拉山隧道岩爆风险总体可控。

表10 典型隧道岩爆情况对比Table 10 Comparison of rockburst conditions of typical tunnels
3 结 论
本文在对66个岩爆隧道的特征参数统计分析基础上,建立了一种通过应力强度比来预测岩爆爆坑深度的岩爆定量化预测模型,并通过室内力学试验、岩体强度损伤准则和地应力场多元线性回归反演,分别得到模型计算所需要的隧道沿线岩体强度及地应力参数,最终对新建CZ铁路色季拉山隧道的岩爆风险进行了定量化预测和相似工程案例对比分析,得到如下结论:
(1)本文根据岩爆隧道爆坑深度与应力强度比线性统计关系所建立的岩爆风险预测模型,可以预测岩爆发生时的最大爆坑影响深度,进而实现对岩爆风险的定量化预测及评估。
(2)色季拉山隧道沿线地应力以水平构造应力为主导,反演出最大水平主应力可达51.24MPa,且地应力普遍较高,同时,硬脆性岩层所占比例较大且均具有较高的岩爆倾向性,具有较高的高地应力岩爆风险。
(3)预测色季拉山隧道可能发生岩爆段落达23254m,占隧道全长的61.25%,其中:中等岩爆风险段落12188m,占隧道全长32.1%,强烈岩爆风险段落3502m,占隧道全长的9.23%。岩爆将主要发生在弱风化花岗岩、闪长岩以及埋深较大的片麻岩段落中,且最大爆坑深度普遍大于1m。
(4)相似工程案例对比分析表明,色季拉山隧道预测最大爆坑深度为3.42m,小于已贯通的巴玉隧道实测最大爆坑深度(3.5m),在合理的施工和防控措施下可认为风险总体可控。
