基于TFIDF+LSA算法的新闻文本聚类与可视化

郝秀慧,方贤进,杨高明

(安徽理工大学 计算机科学与工程学院，安徽 淮南 232001)

0 引 言

在大数据时代，互联网上有大量的数据有待挖掘，面对互联网上大量的文本数据，主要有两种数据挖掘的方法，一种是基于有监督的数据挖掘方法，这种方法一般需要提前对数据进行标注。另一种是基于无监督的数据挖掘方法，这种方法由于不需要提前对数据进行标注，能大大减少人工标注的成本。文本文档聚类作为一种无监督数据挖掘方法，越来越成为数据挖掘领域备受关注的技术。文本聚类主要是将大量的文本集合划分为几个不同的小集合的过程,并使得同一集合内的样本尽可能相似，不同集合内的样本尽可能不相似。文本聚类首先要解决的问题就是文本的表示问题，即对文本数据进行建模。一般使用向量空间模型来表示文本，每个文本都表示为一个向量，向量的值根据不同的技术可有不同的表示方式。一般可以用词频tf或者词频反文档频率(tfidf)权重表示，在这种表示方式中，向量的每个维度为一个单词。为了将无标注数据聚成不同的类别，需要用到聚类算法。聚类算法主要有基于划分的聚类算法[1]、基于层次的聚类算法[2]和基于密度的聚类算法[3]等。其中kmeans作为聚类算法中经典的算法之一，通过划分的方式对数据进行聚类，可应用在大量的数据上。但是kmeans算法也有自身的局限性,如需要事先选择聚类数目K和对初始聚类中心的选择比较敏感等。因此也出现了多种改进kmeans算法，如在文献[1]中有学者根据肘点确定K值，用kmeans++算法来优化kmeans初始中心点的选择[4]等。而面对聚类的一个重要事实是：没有最好的聚类算法，每个聚类算法都是显式或者隐式地对数据施加一个结构[5]。一般来说，评价一个聚类算法的好坏是根据不同的应用来决定，主要可以从三个方面来考虑：聚类的质量、聚类的效率和结果的可视化程度。该文采用不同的方式对数据进行kmeans聚类，用不同的指标来评估聚类的质量，并研究了基于不同聚类方式的算法的效率和结果的可视化程度。

1 文本预处理

1.1 TFIDF算法

TFIDF也叫做词频反文档频率[6]，结合了词频计算公式和反文档频率的计算公式。TFIDF的计算公式如下：

(1)

其中，fij代表词j在文档i中的出现频率,即词j在文档i中出现的频次与文档i中总词数的比，N代表总文档数，nj代表出现词j的文档数。上述公式表示的是当一个词在一篇文章中出现的频次多且在其他文章中出现的次数少时,tfidfij的值是比较大的，也就是表示这个词j对这篇文章i比较重要。解决的是当一个文档中有相同词频的不同词时，区分这些词对文档的重要性问题。例如，词1与词2在文档i中有相同的词频，那这时仅仅用词频来计算词的重要性是不能区分两词的重要性的。通过引入反文档频率，计算这两个词在整个文档集中的反文档频率，若词1在整个文档集中出现的次数较少，而词2在整个文档集中出现的次数较多，那么就说明，词1比词2有更好的文档区分能力。对文档i来说，词1的TFIDF的值就会比词2的TFIDF的值大。

1.2 LSA算法

LSA也称为潜在语义分析[7]，是一种无监督学习方法，主要用在文本的话题分析上，是通过对矩阵进行分解来发现文本与单词之间的基于话题的语义关系。具体实现是将文本集合表示为单词文本矩阵，根据确定的话题个数，对单词文本矩阵进行截断奇异值分解(TruncatedSVD)[8-9]，从而得到话题向量空间，以及文本在话题向量空间的表示。形式化表达分解公式如下：

单词文本矩阵≈单词话题矩阵×话题文本矩阵

潜在语义分析矩阵分解数学公式[8]如下：

Xm×n≈Um×kΣkVk×n

(2)

其中，m是单词的维数，n是样本的个数，k是话题的个数,且k≪n≪m。左奇异矩阵Um×k作为话题向量空间,列由X的前k个互相正交的左奇异向量组成；对角矩阵Σk和右奇异矩阵Vk×n的乘积作为文本在话题向量空间的表示，其中Σk为k阶对角矩阵，对角元素为前k个最大奇异值，Vk×n的行由X的前k个互相正交的右奇异向量组成。

2 TFIDF+LSA算法

由于TFIDF+LSA算法是结合TFIDF算法和LSA算法得来，该文结合两种算法的过程如图1所示。

图1 TFIDF+LSA算法的结合过程

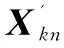
3 聚类算法

3.1 kmeans算法

kmeans算法主要是将数据D={a1,a2,…,an}聚类为k个类别，class={class1,class2,…,classk},目标是最小化平方误差和(SSE)[10]，公式如下：

(3)

其中，centeri是第i个类别的类中心。公式所要表达的含义是计算每类内数据到该类类中心的欧氏距离的和,描述的是每个类类内距离到该类中心的紧密程度,值越小,表示类内越紧密。

kmeans算法步骤如下：

步骤一：选择k个初始中心点，该文采用kmeans++算法来选择k个初始中心点。

步骤二：计算点到k个初始中心的欧氏距离[11]，并将点归类为与初始中心最近的点的类别，依此计算其他点到k个中心的距离，并归类。

步骤三：通过计算每类的均值，更新聚类中心。

步骤四：重复步骤二和步骤三，直至聚类达到收敛条件。

3.2 kmeans++算法

由于kmeans算法的聚类效果受初始中心点选取的影响比较大，因此有学者改进了kmeans算法，即kmeans++算法选择初始中心点的方式是以较大的概率选择离已经选取的聚类中心点最远的点作为下一个初始中心点。算法步骤如下：

步骤一：随机从输入的数据集X中选取一个点作为第一个种子。

步骤二：计算其余点到已经选择的种子中最近的种子的距离D(x)，并以距离的远近为正比计算概率，将概率P最大的那个点作为新的聚类中心,计算公式如式(4)。

(4)

步骤三：重复步骤二直至获得k个种子，即得到k个初始聚类中心。

4 实验和性能分析

4.1 平台与数据

实验采用Windows10系统，Compute Core: 4C+4G, 1.8 GHz,RAM:4 GB.Jupyter notebook,python 3.7.8。数据来源于从校园新闻中采集到的数据，总共11 456条校园综合新闻(新闻网址是：http://news.aust.edu.cn/zhxw.htm)。由于校园新闻主要是对校园活动的记录，每条新闻字数在400字到700字不等。从内容上，主要通过人工的方式，将这11 456条新闻大致分为7个类别，分别为教育教学类、毕业就业类、比赛活动类、思想政治类、交流会议类、学习培训类、管理服务类。采集到的数据集为csv格式，数据情况如表1所示。

表1 采集的部分数据

当采集到文本数据之后，经过数据清洗，包括对文本去重、分词、去停用词等操作后才能进行后续数据的预处理操作。其中，该实验是基于结巴分词得到的分词结果。去停用词的操作主要是建立停用词表，目前比较全的有哈工大的停用词表。该实验使用的停用词表包含有1 214个词，包括特殊符号、不常用的词以及无意义的词等，当然，也可以根据使用的不同语料库和个人实验的需要，增加停用词，建立适合实验需要的停用词表，将分词后不常用的词或者是没有意义的词都可以加入到停用词表中。根据停用词表的不同类别做出部分停用词，如表2所示。

表2 部分停用词表

根据TFIDF+LSA的方法得到的类别划分情况如表3所示。

表3 数据类别划分情况

从表3可以看出，校园综合新闻的数据组成每个类别是不均衡的，最多的有2 418条新闻，最少的有876条新闻。

4.2 聚类评估指标

4.2.1 轮廓系数

轮廓系数(SC)[12]的计算公式如下：

(5)

(6)

公式(5)中，ai表示同一类中样本与其他样本之间的平均距离，bi表示样本与最近的类别内所有样本之间的平均距离。公式(6)中的S(k)是每一类样本轮廓系数的平均值,nk表示第k类聚类的样本数。轮廓系数S(k)的取值在[-1,1]之间，值越接近于1，表示类间分离得越远，聚类效果越好。

4.2.2 卡林斯基-原巴斯指数

卡林斯基-原巴斯指数(CHI)[13]的计算公式如下：

(7)

(8)

(9)

公式(8)中的Bk为类间离差矩阵的迹，公式(9)中的Wk为类内离差矩阵的迹，nE表示数据集E的大小。cq表示类q的中心,cE表示数据E的中心,nq表示q类内的样本数量。CHI的值越大，表示类间数据的分离程度越大，聚类效果越好。

4.2.3 戴维斯-堡丁指数

戴维斯-堡丁指数(DBI)[14]的计算公式如下：

(10)

其中，si表示类i中每一个点到类i中心的平均距离，dij表示类i和类j两个类中心之间的欧氏距离。DBI取值越接近于零，聚类效果越好。

4.3 实验结果与分析

实验采用t-SNE技术[15]对聚类的结果进行可视化展示，这种技术主要是将高维数据映射到低维空间，是一种将高维空间数据看作高斯分布，将低维空间数据看作t分布，将高维映射到低维空间的同时,尽量保证两者分布概率不变的方法。基于TFIDF得到的聚类结果如图2所示，基于TFIDF+LSA得到的聚类结果如图3所示。

图2 基于TFIDF的聚类可视化

4.3.1 聚类可视化结果

从图2和图3可以看出，比起基于TFIDF的聚类结果，基于TFIDF+LSA的聚类结果中，每一类类内更加紧凑，类间可以很好地分离出来。

图3 基于TFIDF+LSA的聚类可视化

4.3.2 不同聚类方式取不同k值的SSE

改变实验中的聚类数目k值，k值依此从2取到20,根据不同的聚类方式得到不同k值下的SSE值，如图4所示。

图4 基于TFIDF聚类和TFIDF+LSA聚类的SSE

从图4可以看出，在相同的k值下，基于TFIDF+LSA的聚类得到的平方误差和SSE更小。整体上，基于TFIDF聚类得到的平方误差和SSE在11 000到10 000之间，基于TFIDF+LSA的聚类得到的平方误差和SSE在6 200到1 000左右。SSE越小，表明聚类的效果越好。

4.3.3 不同聚类方式的评估值对比

不同聚类方式的评估指标值对比如表4所示。

表4 不同聚类方式的评估指标值对比

从表4可以看出，基于TFIDF的聚类和基于TFIDF+LSA的聚类得到的聚类评估指标值相差很大。并且，基于后者聚类得到的SC、CHI和DBI都比前者好，其中基于TFIDF+LSA聚类得到的SC的值约是基于TFIDF聚类得到的值的23倍，CHI的值约是基于TFIDF聚类得到的值的35倍，而DBI的值约是基于TFIDF的值的0.16倍。即基于TFIDF+LSA的聚类得到的聚类结果比基于TFIDF的聚类结果好。

4.3.4 不同聚类方式时间对比

从图5可以看出，基于TFIDF的聚类方式所需的聚类时间远远高于基于TFIDF+LSA的聚类时间，表明基于TFIDF+LSA的聚类方式的聚类时间更短，速度更快。且基于TFIDF聚类的时间约是基于TFIDF+LSA聚类的55倍。

图5 不同聚类方式的聚类时间

4.3.5 实验结果分析

综上，基于TFIDF+LSA的聚类得到的聚类结果比基于TFIDF的聚类结果好，主要是因为前者使用了潜在语义分析算法，将单词文本矩阵分解为单词话题矩阵和话题文本矩阵。也即前者在聚类时使用到了话题文本矩阵进行聚类，而后者是使用单词文本矩阵进行聚类。使用前者聚类一方面可以将原始矩阵进行了降维，提取了矩阵的话题信息，另一方面同一话题内的词的词义更相近，有利于更好地聚类。

而且，由于kmeans算法聚类的时间复杂度为O(mnkt),其中m是样本的维数，n是样本的个数，k是聚类个数，t是迭代次数。而基于TFIDF+LSA的聚类方式的时间复杂度为O(knkt)，即将m维降到了k维，也就降低了聚类整体的时间复杂度，提高了聚类速度，降低了聚类时间。同时从空间复杂度上分析，基于TFIDF的聚类方式所需要的空间为O(mn),基于TFIDF+LSA的聚类方式所需的空间复杂度为O(kn)，其中k是远远小于m的。因此，与基于TFIDF的聚类方式相比，基于TFIDF+LSA的聚类算法也减少了空间复杂度。

5 结束语

将TFIDF算法和LSA算法相结合，提出基于TFIDF+LSA聚类方式，通过计算TFIDF值来得到词在文本中的权重，然后将得到的TFIDF权重矩阵运用潜在语义分析LSA算法来得到文本的话题表示，最后，用kmeans算法对话题文本矩阵进行聚类而不是用单词文本矩阵对数据进行聚类。该文将这种方法应用到了实际的新闻文本数据聚类上，实验结果表明，该方法大大提高了中文文本聚类的速度和可视化效果，可以对大规模的文本数据产生实际的应用价值。另一方面，在研究过程中也存在一些比较难以处理的问题，比如说，人工根据文本的内容将新闻文本分为某一类，实际上，一篇文章有可能是关于多个话题的，即可能是属于多个类的，在这种情况下，若后续对文本进行分类处理，研究其准确率等分类指标的时候，对于这种情况，只要这篇文章属于正确话题中的某一个，那么就算是分类正确的。