机理与数据融合的航天器控制系统数字孪生建模方法
2022-08-02宁之成刘潇翔王淑一
宁之成, 刘潇翔, 王淑一
北京控制工程研究所,北京 100094
0 引 言
航天任务的不断多样化、复杂化向航天器控制系统的可靠性和准确性提出了更高的要求.构建高精度、多物理特性的航天器部件模型不仅能在航天器控制系统设计阶段提供更贴近真实部件的输出,还能够对在轨运行的部件及系统可能出现的情况进行模拟,进而更好地为航天器控制系统的故障诊断、故障预警、寿命预测等服务.
航天器控制系统的典型部件包括陀螺、飞轮、星敏感器、太阳敏感器、星载计算机等.传统的对于部件的建模大多从部件的机理出发构建部件的数学仿真模型[1-5].但基于机理建立的模型在航天器高品质控制中存在着以下两个问题:
1)在建模精度方面,基于机理建立的模型通常将一些因素进行简化处理,这使得所建立的模型与实际情况存在差异.此外,引起航天器控制系统部件输出误差的原因包含许多不确定因素,如加工误差、材料特性等.这些在进行部件建模时通常难以考虑进去.
2)从数据利用上看,传统建模难以提取可获得的地面测试数据、在轨遥测数据中的信息,无法根据加工制造后获得的实测数据对模型进行更新.
这就意味着航天器控制系统的建模方式面向高精度控制和长期自主健康管理等需求,需要考虑如何将机理与数据融合起来,建立航天器控制系统的孪生级模型.数字孪生作为一种从航天领域提出的概念,近年来在各领域均有拓展和应用[6-7].航天器控制系统的数字孪生建模能够充分地利用机理知识和数据实现对建模对象的高精度模拟.
针对当前航天器控制系统模型精度不足和特性维度不够等问题,本文提出一种机理与数据融合的数字孪生建模方法.首先构建控制系统部件可正向建模的精细机理模型,在此基础上通过LSTM网络对可获得的数据进行信息提取,将其补充到机理模型上.以飞轮典型的机、电、热耦合部件机理模型和数据修正的仿真结果,验证了数字孪生建模的可行性和有效性.
1 航天器控制系统数字孪生建模方法
1.1 基本原理
数字孪生建模是在正向机理建模的基础上,基于数据驱动,通过机器学习、深度学习解决机理模型无法描述的非线性、不确定性、进化性问题,即结合模型驱动和数据驱动的方式建立物理对象高逼真度的虚拟模型.建立的数字孪生体能够精准地模拟物理对象在真实空间行为、特征、性能等,并能够根据数据不断地进行更新使模型能够更加逼近物理对象在真实环境中状态.基于数字孪生的定义,本文提出的机理与数据融合的数字孪生模型如图1所示.
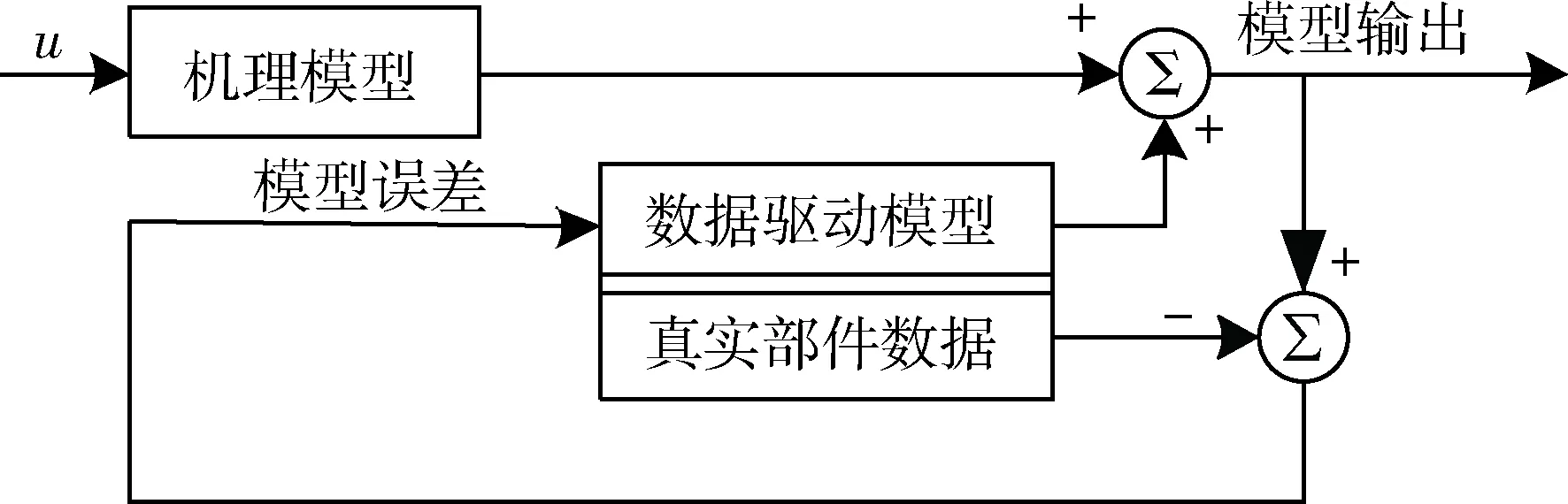
图1 机理数据融合的数字孪生模型Fig.1 Digital twin model of mechanism data fusion
本文的机理模型建模分为两部分.一部分是基于工作原理建立的输入输出传递关系模型,另一部分是对已知的干扰建立合适的干扰特性模型.
1.2 数据驱动建模的神经网络选取
控制系统的输入输出按照时间先后顺序记录的一系列数据可以作为一个时间序列.控制系统由于受到各种干扰因素的影响在输入输出的时间序列上会包含各种误差.同时,实际物理系统在连续时间序列上的输出会存在状态延续性可以认为时间序列反映了系统的内在规律[8].通过挖掘时间序列中的信息将其补充到机理模型上能够更好地模拟系统的输出.长短期记忆网络(long short-term memory, LSTM)由于其独特的设计结构在处理序列数据时能够有效地挖掘出数据的短期特征和长期特征[11].航天器控制系统输入输出连续时间序列中同时存在短期的干扰信息和长期的退化信息.因此,在数据驱动建模的神经网络选取上,通过LSTM网络对机理模型和真实数据之间的偏差进行学习,并将其补充到机理模型上,以提高模型精度.
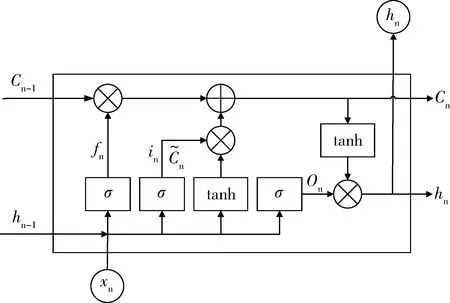
图2 LSTM神经元模型Fig.2 LSTM neuron model
LSTM 网络是由一个个LSTM神经元组成,每一个神经元在n时刻有3个输入:细胞状态Cn-1、隐层状态hn-1和n时刻的输入xn.输出为细胞状态Cn和隐含层状态hn.LSTM单元的更新过程可用如下公式表示:
(1)
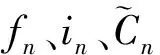
根据航天器控制系统的输入输出时间序列数据的规模和特征选择合适的LSTM网络结构完成LSTM的搭建.
2 典型部件机理建模
飞轮作为航天器控制系统的执行机构,对于航天器姿态控制十分重要.此外,飞轮一般由滚动轴承、电机、密封壳体、轮体4部分组成,具有结构复杂、模型参数多、扰动特性丰富等特点.因此,本部分选取飞轮为研究对象,验证提出的航天器数字孪生建模方法的可行性和有效性.
2.1 输入输出传递关系建模
飞轮理想情况下的输入输出关系可以通过动量矩定理、牛顿第三定律和电机驱动关系推导出[2].考虑到实际中可能存在的微量损耗力矩,因此飞轮的输出力矩可以表示为
Tc=Tm-Td
(2)
式中,Tc为飞轮实际输出力矩,Tm为飞轮电机的驱动力矩,Td为飞轮的损耗力矩.
飞轮实际输出力矩与输出角动量之间满足如下关系:
(3)
式中,H(t)表示飞轮角动量,J表示飞轮转动惯量,ω(t)表示飞轮转速.
飞轮电机的驱动力矩Tm满足直流电机方程,
Tm=ktim(t)
(4)
(5)
式中,kt表示电机力矩系数,im(t)表示电机电枢电流,Tr为飞轮控制力矩指令,Gd表示电机控制器驱动增益、ωd表示电机控制带宽,s为Laplace算子.
根据牛顿第三定律,飞轮控制力矩Tz满足
Tz=-Tc
(6)
综上,飞轮的输入输出传递关系模型如图3所示.
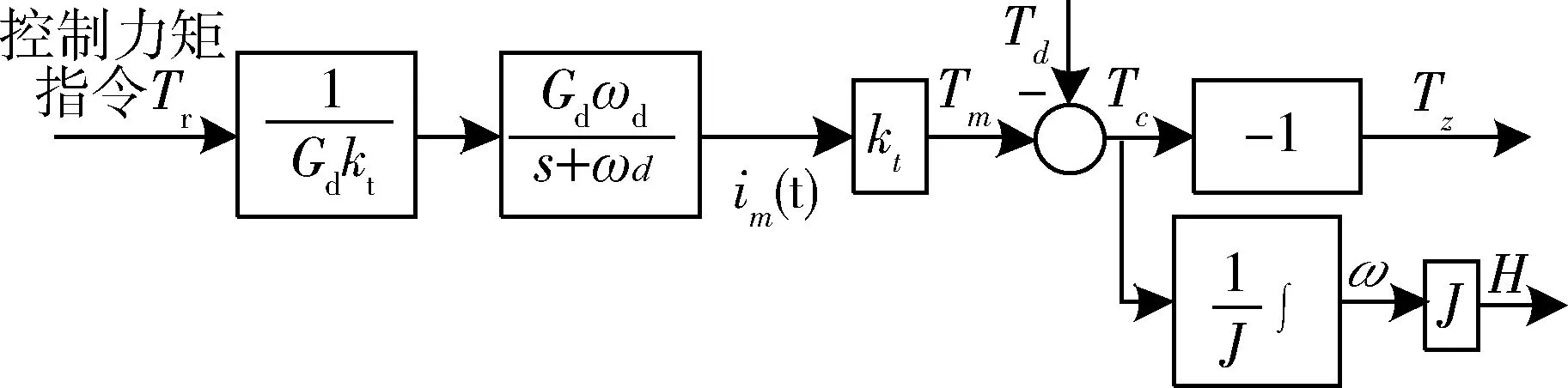
图3 飞轮理想数字仿真模型Fig.3 Ideal digital simulation model of fly wheel
2.2 干扰特性建模
实际上飞轮在工作时会受到各种因素的干扰.为了准确描述飞轮输入指令和输出力矩之间的关系对飞轮的干扰因素进行建模.本文选取Goodrich公司生产的ITHACO-A型反作用飞轮进行建模[12].这里主要考虑飞轮反电势力矩限制、摩擦力矩、动静不平衡干扰、电机干扰的影响.
(1)反电势力矩限制
在电机处于低电压工作的情况,如果飞轮转子转速很高,此时飞轮输出的力矩将受到反电势作用的明显影响.同时,母线电压和母线电流之间的关系[12]可表示为
(7)
其中,Ibus为反电势力矩限制情况下的干扰电流,im为电机电流,Vbus为母线电压,ke为反电势系数,ω为飞轮转速,RB为母线电阻.
(2)摩擦力矩
本文采用学者Dahl提出的Dahl模型来表征摩擦力矩[4].考虑粘性摩擦和Dahl模型表征的低速摩擦时,反作用轮摩擦模型可表示为

(8)
其中,sign为符号函数,Tf为总的摩擦力,Tf1为轴承固体摩擦力矩,Tf0为库仑摩擦力矩,Tf2为润滑剂粘性摩擦力矩,ω为飞轮转速,D为阻尼系数,β为轴承静止斜坡参数,量纲为(N·m·rad)-1.
(3)动静不平衡干扰
飞轮由飞轮转子质量分布不均匀导致的静不平衡和动不平衡是飞轮的主要干扰之一[4].静不平衡主要是由转子的质心偏离几何中心或惯性轴而产生了干扰力.此时可将飞轮看成严格轴对称部分和距离飞轮rs处的质量点ms.飞轮在星体和转轴垂直两轴上引起的干扰力可表示为
Fx,y=msrsΩ2sin(ωt+α0)
(9)
式中,α0为初始相位.
动不平衡是指由于转子的惯性轴和旋转轴线没有重合而产生了干扰力矩.此时可将飞轮质量分为严格对称部分和沿着旋转轴方向距离为2h的点质量md,且距离转轴均为rd.动不平衡引起的干扰力矩可表示为
Tx,y=2mdrdhω2sin(ωt+β0)
(10)
式中,β0为初始相位.
实际工程中,由于转子及结构的振动特性,导致飞轮的输出干扰与干扰力矩会包括多于飞轮旋转频率的干扰成分.根据文献[13],动静不平衡带来的干扰可描述为
(11)
其中,m(t)是扰动力或扰动力矩,n是模型中含有的谐波数,ω为飞轮转速,hi是第i次谐波数,Ci为与m(t)相应的第i次谐波的幅值,单位为N/Hz2或N·m/Hz2,αi为随机相位角,假定均匀分布在[0,2π].
(4)电机干扰
飞轮一般采用永磁无刷直流电机作为驱动电机.根据转矩波动的根源不同,可将无刷直流电机的波动转矩分为齿槽转矩和纹波转矩.根据文献[12]可将齿槽转矩和纹波转矩表示为
(12)
TC=TmCsin(3Ntω)
(13)
其中,B为齿槽转矩幅值,C为纹波转矩幅值比例系数,TB、TC分别为齿槽转矩和纹波转矩,N为电机极对数,ω为飞轮转速.
考虑飞轮的工作原理和各种影响因素,飞轮的机理模型可以表现为图4.
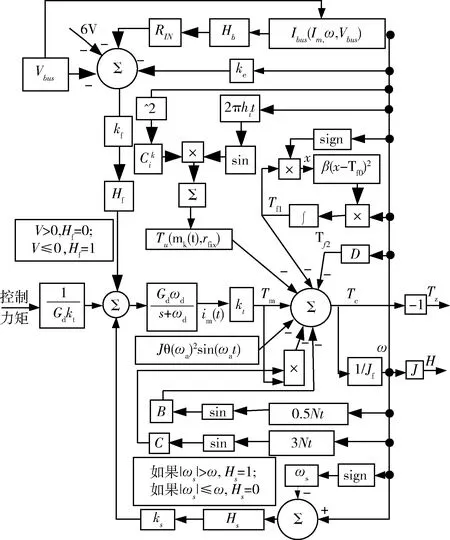
图4 飞轮详细机理模型Fig.4 Detailed mechanism model of fly wheel
3 基于LSTM的数据驱动建模
飞轮的机理模型中无法对飞轮受到的不确定因素和环境因素影响导致参数变化部分进行建模.通过对飞轮数学模型中的部分参数进行调整来模拟具有建模误差的物理实体部件特性.基于LSTM网络对飞轮机理模型输出和模拟物理实体输出之间的偏差进行学习,建模误差的学习结果补充到飞轮机理模型上,而实现飞轮的机理+数据驱动建模.飞轮物理实体参数设置如表1所示.
以阶跃指令力矩为例,指令力矩在第2 s的时候发生阶跃.飞轮机理模型与模拟物理实体之间的偏差如图5所示.
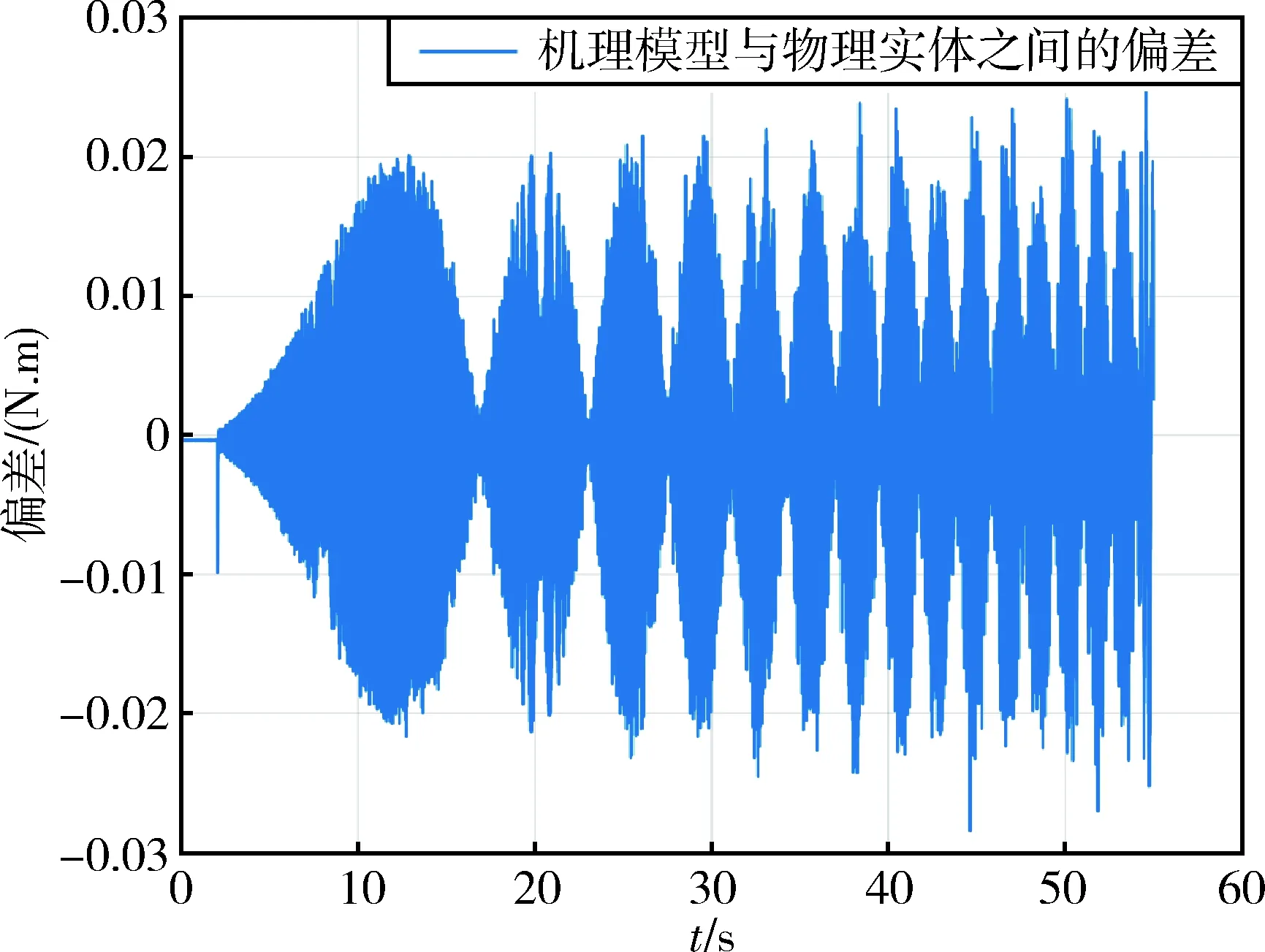
图5 机理模型与物理实体之间偏差Fig.5 Deviation between mechanistic model and physical entity
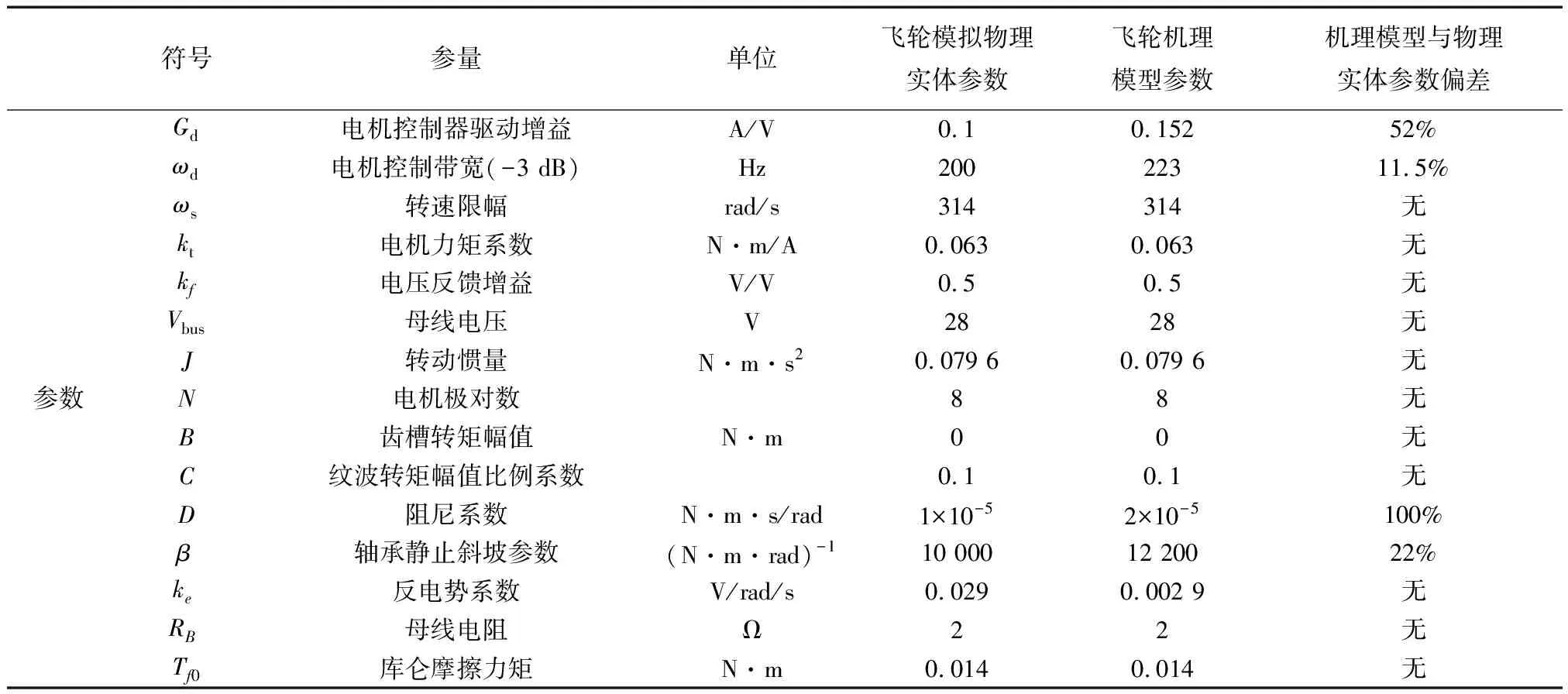
表1 飞轮物理实体参数设置Tab.1 Fly wheel physical entity parameter setting
对于飞轮机理模型和模拟物理实体之间的偏差数据,通过LSTM网络进行学习.数据集从图5所示发生阶跃后的偏差数据中选取.采样时间为0.01 s,共采样5 000个点.取前90%作为训练集,后10%作为测试集. 以LSTM网络输出数据和偏差数据的均方差为评判标准,调整LSTM网络参数,选择学习效果最好的网络.
3.1 参数优选
在进行LSTM网络参数调整时需要根据测试集结果对LSTM的损失函数、LSTM网络分割窗口长度、隐含层数、每个隐含层所含神经元个数、学习率、一次训练抓取数据样本数量(batch)等参数进行优选.在训练过程中,对结果影响较大的关键参数有损失函数、分割窗口长度、batch大小.当取LSTM网络为两层隐含层、每层隐含层所含神经元个数为128、学习率为0.001时3个关键参数的选取对学习效果的影响如下所示:
1)损失函数
均方误差损失函数是通过计算预测值和实际值之间的平方差的平均值来评价网络学习效果.DTW是一种计算两个时间序列相似度的方法[14- 15].LSTM网络的学习效果可以通过DTW计算预测值时间序列和输入时间序列之间的不一样程度来表示.以3个例子来比较两种损失函数的优劣.
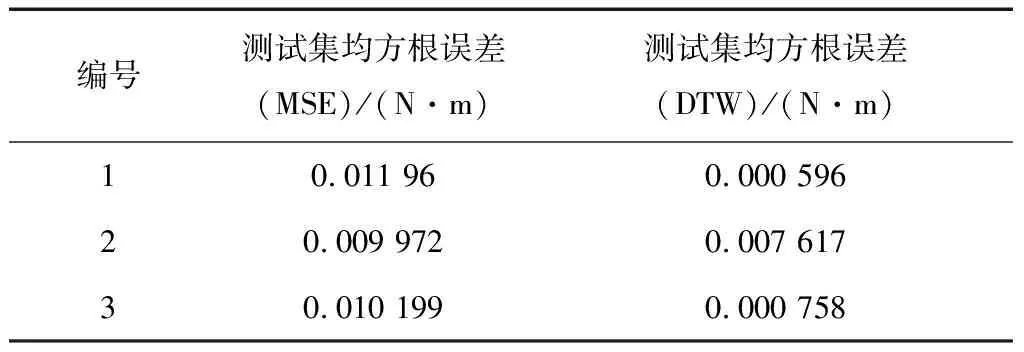
表2 两种损失函数结果比较Tab.2 Comparison of results of two loss functions
从统计结果可见,DTW作为损失函数相较于MSE能够更好地学习飞轮偏差时间序列数据中的信息,因此选取DTW作为LSTM网络的损失函数.
2)分割窗口长度
数据在进入LSTM网络前,需要将数据分割成一个个样本,每个样本的时间序列长度即为分割窗口长度.在损失函数取DTW、batch取256时,不同的分割窗口长度对LSTM结果的影响如表3所示.
根据统计结果来看,分割窗口长度需要适当.本文选择局部最优的250作为LSTM网络的分割窗口长度.
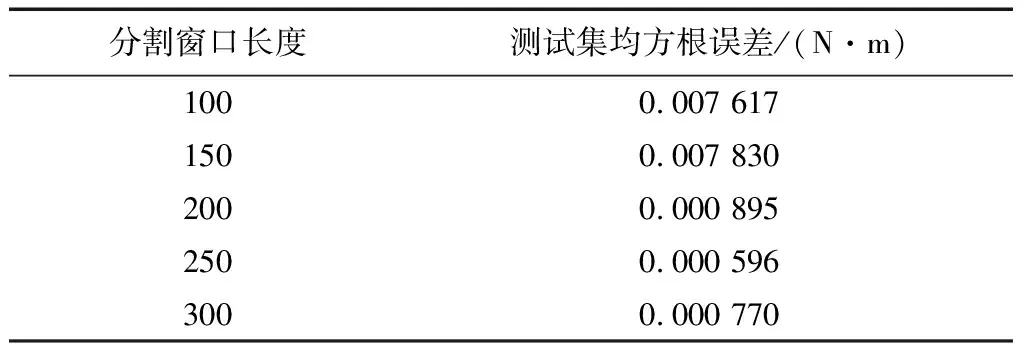
表3 分割窗口长度对结果影响Tab.3 Effect of split window length on results
3)一次训练抓取数据样本数量(batch)
由于不能访问整个数据集上的真实梯度,需要用有限的batch大小来近似梯度.当batch过小时LSTM学习容易受到噪声的影响,batch过大会导致模型过大,同时影响网络泛化能力.从统计结果来看,当取batch大小为256时,网络学习效果取得局部最优,因此选取batch大小为256.
综上,当取LSTM为两层隐含层、隐含层神经元个数为128、损失函数取DTW、分割窗口长度取250、batch大小取256、学习率取0.001时网络学习效果取得局部最优.学习效果如图6所示.
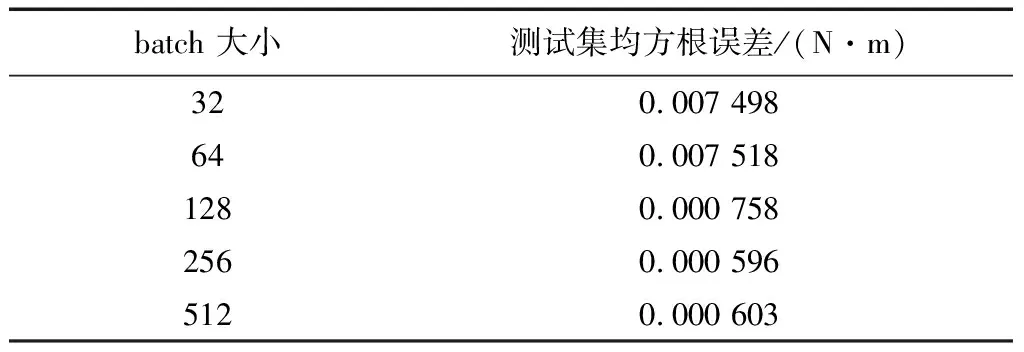
表4 batch 大小对结果的影响Tab.4 Effect of batch size on results
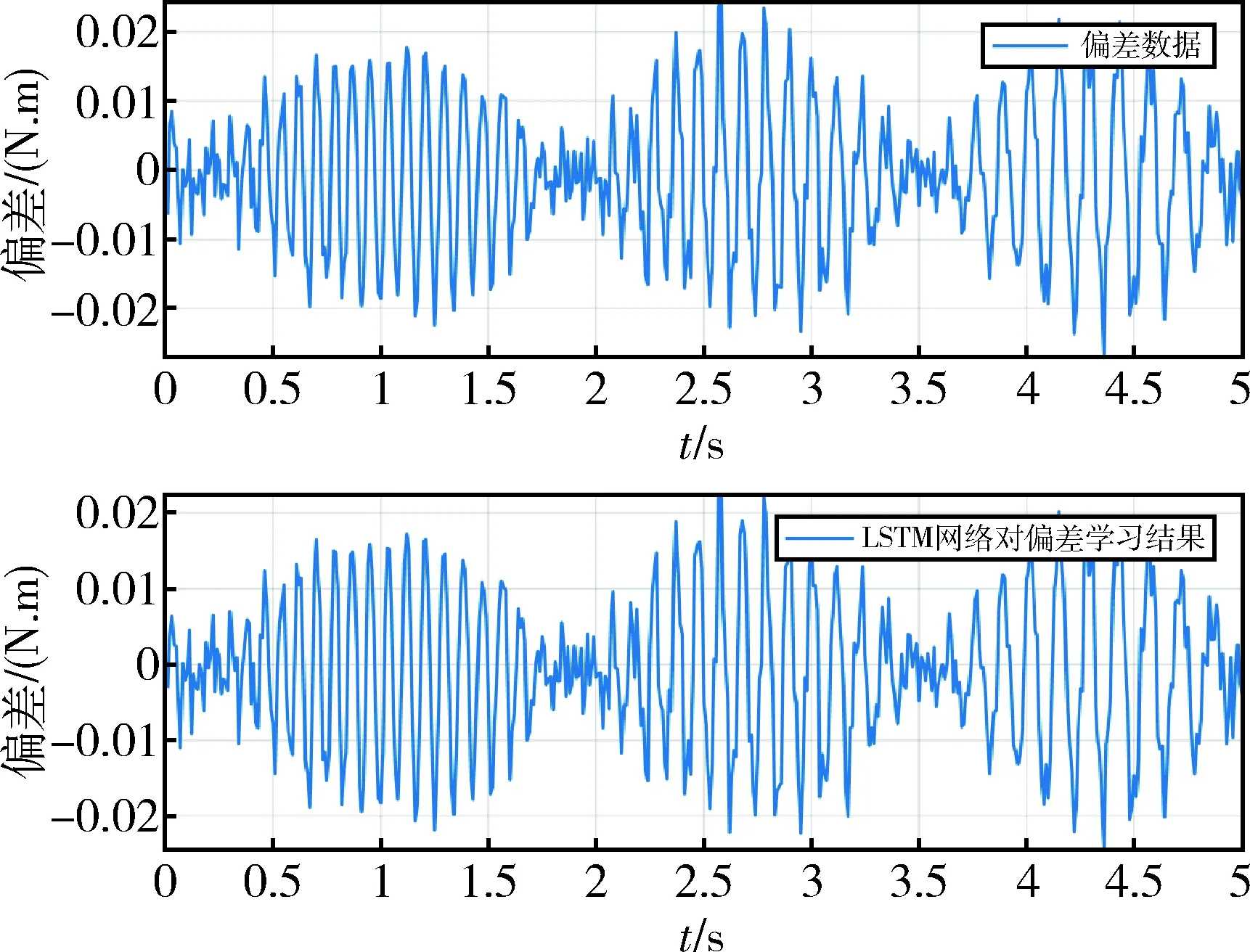
图6 偏差数据与LSTM网络学习结果Fig.6 Deviation data and LSTM network learning results
从仿真结果可以看出,LSTM网络能够较好地学习偏差数据.再将LSTM网络对偏差的学习结果补充到飞轮的机理模型上,即可完成飞轮的机理与数据融合的数字孪生建模.
4 数字孪生建模精度分析
对飞轮的机理模型和数字孪生模型进行仿真测试,比较其模型精度.
首先对飞轮机理模型进性仿真验证,模型参数设置如表1所示.分别输入正弦、阶跃、斜坡3种典型的控制指令力矩时,飞轮仿真模型的输出如图7所示.
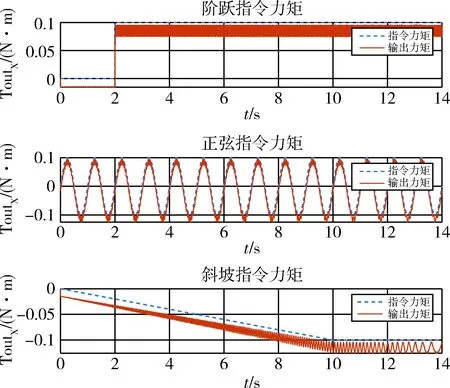
图7 飞轮机理模型仿真输出Fig.7 Fly wheel mechanism model simulation output
从仿真结果可以看出,该飞轮机理模型合理,能够根据指令力矩的各种形式输出相应的控制力矩.但机理模型由于难以捕捉数据信息,相对模拟物理实体的误差较大.以阶跃力矩的响应为例,机理模型与模拟物理实体之间的偏差如图5所示.
基于LSTM的数据驱动模型与机理模型结合得到飞轮的数字孪生模型.数字孪生模型的参数选取3.1节取得局部最优的网络参数.飞轮机理模型误差和数字孪生模型误差仿真结果如图8所示.
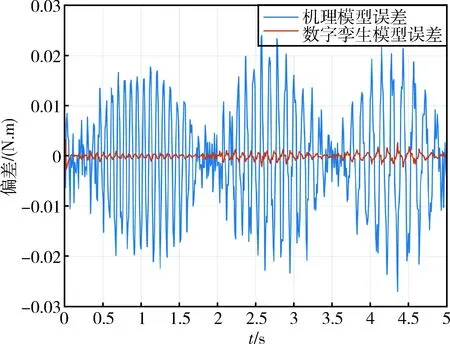
图8 机理模型与数字孪生模型误差对比Fig.8 Mechanistic model and digital twin model comparison
从图8可以看出,飞轮数字孪生模型输出误差远小于机理模型输出误差,本文所提出的数字孪生建模方法能够较大地提高复杂多物理特性耦合的建模精度.
5 结 论
提出的基于机理和数据融合的控制系统数字孪生建模方法能够充分利用已有的机理知识和数据,对部件的特性进行精准的刻画,提高了建模的精度.此外,模型具有实时数据驱动的更新能力,能够根据地面测试或在轨飞行试验获得的数据对数字孪生模型做进化更新,使得模型输出能够反映物理实体的实时状态,为航天器控制系统在轨实时性能评估、健康预测及故障处理等提供基础.
