磁悬浮旋转关节建模及解耦控制方法研究
2022-08-02赵同爽张激扬王英广樊亚洪罗睿智
赵同爽, 张激扬*, 王英广, 樊亚洪, 罗睿智
1. 北京控制工程研究所,北京 100194 2. 精密转动和传动机构长寿命技术北京市重点实验室,北京 100194
0 引 言
目前,遥感卫星多使用推扫成像[1-3]或机动成像[4-6]模式.其中,推扫式成像卫星具有机动性好、图像分辨率高等优点,但同时存在成像幅宽较窄、视野有限等不足.机动成像卫星虽具有较大的扫描幅宽,但其姿态机动过程含变速阶段,存在成像精度低等问题.综合两者优点,遥感卫星通过使用环扫成像[7-9]方法,可具备超宽幅成像能力.
传统卫星通常使用机械轴承连接载荷舱和平台舱.随着空间技术的发展,对卫星平台指向精度和稳定度要求不断提高,机械轴承因隔振性能较差,润滑困难,磨损高等缺点渐显不足.与之相比,洛伦兹力磁轴承(LFMB)可实现定、转子的无接触支承[10],具有隔振性能好,无磨损,刚度可调等优点[11],可被应用于航天器高精度执行机构等领域[12-18].相较于其他类型磁轴承,LFMB开环稳定,且其电磁力与控制电流基本呈线性关系,易于控制系统设计,因此选用LFMB作为磁悬浮旋转关节中的轴、径向磁轴承.
载荷舱在轨与旋转关节上平台转子固连,平台舱与下平台固连.载荷舱三轴平动及转动控制需依靠磁悬浮旋转关节和平台舱实现,因此磁悬浮旋转关节的控制策略对载荷舱精稳运动性能至关重要.载荷舱在轨进行六自由度运动,可采用分散控制方式,即只针对位移传感器处的偏移值进行控制,但其会使载荷舱平动量和转动量耦合,不易调节控制参数.本文通过解耦控制方式,将控制力与力矩分开,可达到平动自由度与转动自由度之间解耦的目的[19].文献[20]针对磁悬浮陀螺转子径向转动自由度间存在的耦合问题,提出了一种前馈解耦内模控制方法,通过设计前馈解耦矩阵实现了陀螺转子偏转的完全解耦.
综合调研结果,未见到与洛伦兹力磁悬浮旋转关节建模和控制系统设计相关的研究发表.本文以洛伦兹力磁悬浮旋转关节为研究对象,建立其动力学模型,并设计了解耦控制器及其优化方法提升系统的动态性能.通过仿真分析和实验验证表明:旋转关节控制系统稳定且完全能控,控制器优化方法可使系统稳定性和控制性能获得较大幅度的提升.
1 旋转关节结构设计与建模
1.1 旋转关节结构设计
以旋转关节样机为研究对象,其结构示意图如图1所示(转子质心or位于上、下径向位移传感器之间).旋转关节下平台与地面固连,上平台转子通过卸载轴承将重力卸载后可稳定悬浮,其轴向(即x轴方向)平动由轴向LFMB控制,轴向转动由旋转电机控制.由图1可知,通过上、下4组径向LFMB(图1中未画y方向磁轴承)提供y方向和z方向的控制力,可合成径向控制力和力矩,控制上平台转子y、z方向的平动及转动.
位移传感器、控制器、径向LFMB转子线圈均固连于上平台转子.其中Lma、Lmb分别为上、下径向磁轴承到转子质心的距离,Lsa、Lsb分别为分别为上、下径向位移传感器到转子质心的距离.
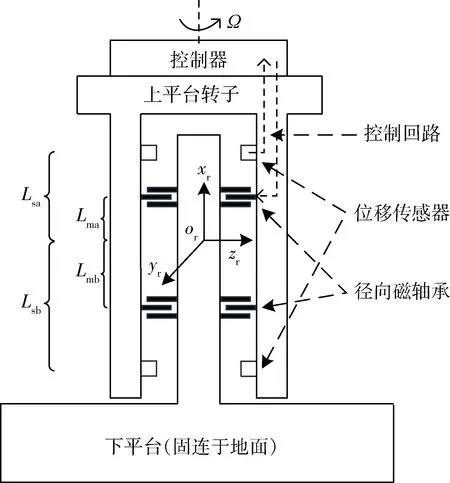
图1 旋转关节结构示意图Fig.1 Schematic diagram of the rotary joints
定义建模中使用到的坐标系:以上平台转子质心or为坐标原点建立转子坐标系orxryrzr,其中xr轴为旋转主轴,yr轴和zr轴分别指向两组径向磁轴承线圈的中心,并与xr轴满足右手定则;以地心为原点建立惯性坐标系oixiyizi,初始时惯性坐标系与转子坐标系三轴重合.
1.2 洛伦兹力磁轴承建模
LFMB的结构如图2所示,左侧为俯视图,右侧为剖面图,其主要包括定子磁钢、转子线圈两部分.

图2 LFMB结构图Fig.2 Structure diagram of LFMB
忽略磁路漏磁和线圈自感磁场的影响,根据等效磁路法,得到线圈主磁通Φm和磁感应强度B的数学表达式为
(1)
B=[BiBo]T=[diag{Ai,Ao}]-1[ΦmΦm]T
(2)
式中,Fpi=Hclpi,Hc为磁钢的矫顽力,lpi为磁钢的磁化长度,Rpi为对应磁钢的磁阻,Rco和Rci分别为外磁钢和内磁钢间穿过转子线圈的气隙磁阻,Bi和Bo分别为内、外磁钢气隙的磁通密度,Ai和Ao分别为内、外磁通密度对应的等效截面积.
由图2俯视图可看出转子4个线圈沿径向均匀分布,每个线圈为两个同心圆的一段拼接而成,所对应的圆心角为φ,内径为li,外径为lo.取其中一个线圈受力分析,如图3所示.

图3 磁轴承线圈受力分析Fig.3 Force analysis of LFMB coil
设线圈中电流为I,匝数为N,取外侧线圈中长度为dl的电流元Idl.因磁场与线圈平面垂直,则此电流元所受电磁力为
dF=NIdl×Bo
(3)
通过积分运算可得
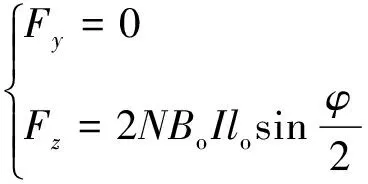
(4)
因每组线圈通以大小相等、方向相反的电流,其在磁场中受到大小相等、方向相同的电磁力,则每组线圈对上平台转子提供的径向力为
(5)
将式(1)、(2)代入式(5)可得
(6)
在工作范围内,磁轴承的磁化长度、磁阻基本不变,即磁轴承电磁力与控制电流基本呈线性关系,电流刚度可近似为常数.则磁轴承对旋转关节上平台转子提供的控制力可近似为
Fr=KiI
(7)
式中,Ki为磁轴承电流刚度.
1.3 上平台转子动力学建模
上平台转子的动力学分析需在惯性坐标系下进行,定义由惯性坐标系oixiyizi到转子坐标系orxryrzr的旋转矩阵为
(8)
式中,α为上平台转子绕xi轴的旋转角度.
则Fr由转子坐标系转换到惯性坐标系下为
(9)
式中,Fr=[FrayFrazFrbyFrbz]T为磁轴承提供的控制力在转子坐标系下的表示,Fi=[FiayFiazFibyFibz]T为磁轴承提供的控制力在惯性坐标系下的表示,下角标a和b分别代表上、下径向磁轴承.
根据旋转关节结构进行受力分析可知,通过调节上、下磁轴承的控制力,可产生偏转力矩,控制上平台转子径向偏转.由受力分析得
(10)
式中,Fy和Fz、My和Mz为径向磁轴承对转子提供的控制力和力矩在yi和zi方向上的投影.
上平台转子平动动力学方程为
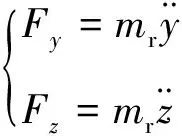
(11)
式中,mr为上平台转子质量,y、z为转子质心径向位移.
根据转子动力学,可得上平台转子在惯性坐标系下的偏转动力学方程为
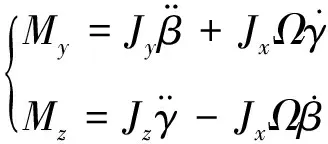
(12)

联立式(7)~(12)可得上平台转子的线性化动力学方程为
(13)
2 控制器设计
2.1 解耦控制器
由式(13)可知,上平台转子动力学中平动和转动本不耦合,而通过式(18)~(19)可知,经位移传感器测量后上平台转子的平动量和转动量耦合在一起,因此设计解耦控制器将平动量和转动量分开进行控制.
因控制器和位移传感器均固连于转子,控制律需基于转子坐标系设计.根据上文,磁轴承产生的控制力和力矩模型为
(14)
(15)
针对上、下径向磁轴承,对位移传感器测量值进行单位负反馈控制,可得磁轴承的控制电流为
(16)
(17)
式中,gY(s)、gZ(s)为磁轴承电流的控制率,Ay、Az为上径向位移传感器测量值,By、Bz为下径向位移传感器测量值.
根据传感器测量原理,位移传感器测量值可近似为上平台转子质心平动和转动在传感器处引起的偏移值,即
(18)
(19)

联立式(14)~(19)可得到磁轴承控制力和上平台转子的位姿关系
(20)
(21)
令
(22)
(23)
可得到磁悬浮旋转关节的控制律为
(24)
(25)
式中,gy(s)、gz(s)负责转子y、z方向的平动控制;gβ(s)、gγ(s)负责转子y,z方向的转动控制.
将式(24)、(25)代入式(16)、(17)可得磁轴承的解耦控制律为
(26)
(27)
解耦控制律中g(s)采用PID控制方式
(28)
控制器输入为平动量或转动量时,其对应的PID控制参数不同.其中比例控制为磁轴承提供了一定的支撑刚度,积分控制对磁轴承的径向偏转误差进行积累和控制,微分控制为磁轴承提供一定的阻尼.
2.2 控制器优化
由实验结果可知,控制器未优化时,系统阶跃响应的超调较大,调节时间过长,考虑是系统相角裕度小、阻尼过低导致的.尝试通过增大kD来增加系统阻尼,但其会使系统在高频段的幅值增益过大,易激发系统的结构模态(受篇幅所限,高频幅值增益对系统结构模态的影响在本文中不详细展开).因此设计相位补偿器,仅在低频段增大系统相角,增加系统阻尼.
根据仿真及实验调参结果,设计相位补偿器在ωm=4.6 Hz处(系统控制模态附近)将系统相角提高φm=10.7°,此时控制器优化效果较好,系统振荡明显衰减.根据上述参数,可设计相位补偿器如下:
(29)
通过在控制器前端串联相位补偿器,完成控制器的优化,可在低频段提升系统相角,增大系统阻尼,增强系统稳定性.控制器优化后,可得最终的解耦控制律为
(30)
(31)
加入相位补偿器后,旋转关节控制系统的结构框图如图4所示.

图4 洛伦兹力磁悬浮旋转关节控制系统结构框图Fig.4 Block diagram of the control system of the Lorentz force magnetically levitated rotary joints
3 系统性能分析
基于表1所示的磁悬浮旋转关节实测物理参数,建立仿真系统模型.因上径向磁轴承在转子质心下方,为便于计算,定义Lma为负值(参考图1).
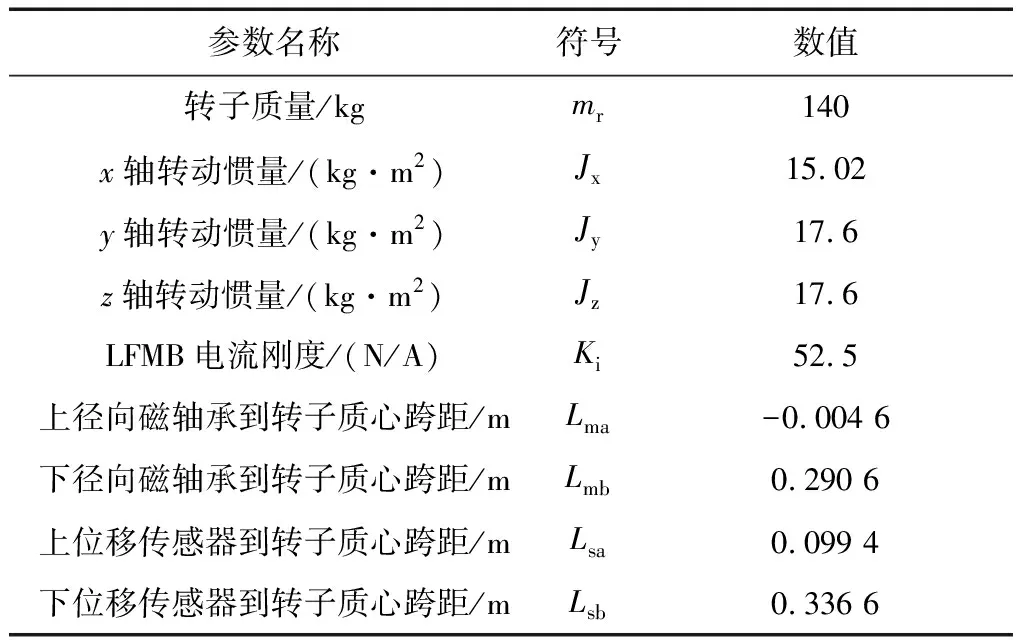
表1 旋转关节物理参数Tab.1 Physical parameters of the rotary joints
3.1 系统能控性证明
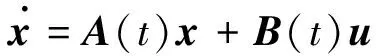
(32)
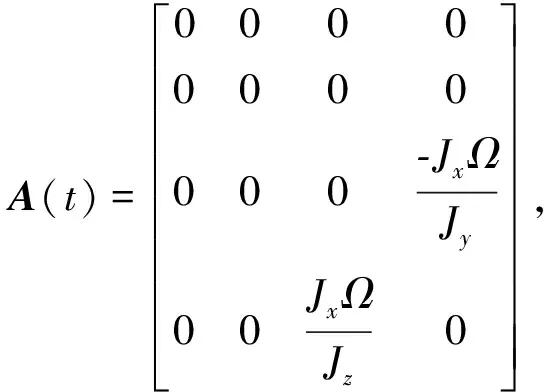
因磁轴承线圈安装于转子上,导致磁轴承对上平台施加的控制力和力矩随时间变化,系统成为连续时间线性时变系统.定义如下矩阵:
(33)
若对任意有限时刻t∈J均有
rank[M0(t)⋮M1(t)⋮M2(t)⋮M3(t)]=4
(35)
则根据线性时变系统的能控性秩判据,可证明系统在任意有限时刻都完全能控.即对任意初始时刻t0∈J,均存在时刻t1∈J,t1>t0,通过控制电流u(t),t∈[t0,t1]的控制,系统可由初始偏离状态x(t0)=x0转移到稳定状态x(t1)=0.
对矩阵M0(t)进行初等行变换(Ωt=kπ/2点暂不考虑)得阶梯矩阵

(35)
式中,q(t)=Lmbcos2Ωt-Lmasin2Ωt-Lmb,h(t)=sinΩt·cosΩt,Lm=Lma+Lmb.
因(Ki/mr)≠0,(Ki/Jy)≠0,Lm≠0,故rank(M0(t))=4在Ωt≠kπ/2时恒成立.再将Ωt=kπ/2代入M0(t)中,亦可得rank(M0(t))=4.及对任意有限时刻t,rank[M0(t)⋮M1(t)⋮M2(t)⋮M3(t)]=4恒成立,故可证明:系统在任意有限时刻完全能控.
3.2 平动控制系统稳定性分析
解耦控制中的平动控制器负责上平台转子y、z方向的平动.得到平动控制系统在控制器优化前的闭环零、极点分布如图5:
可知系统有一对共轭复数极点(-4.69,±16.49j),其附近处为一对共轭复数偶极子,且在零点附近实轴上分布了4个偶极子:(-0.3,0j)、(-0.28,0j)、(-0.008,0j)、(-0.006,0j).根据经典控制理论,因上述偶极子距原点较远,其对系统动态性能的影响可以忽略.则根据闭环主导极点的选取规则,选共轭复数极点(-4.69,±16.49j)为平动控制系统的闭环主导极点.则旋转关节平动控制系统可被简化为二阶系统.图5中角β为系统阻尼角,可求得等效系统的阻尼比ξt=cosβ=0.27.
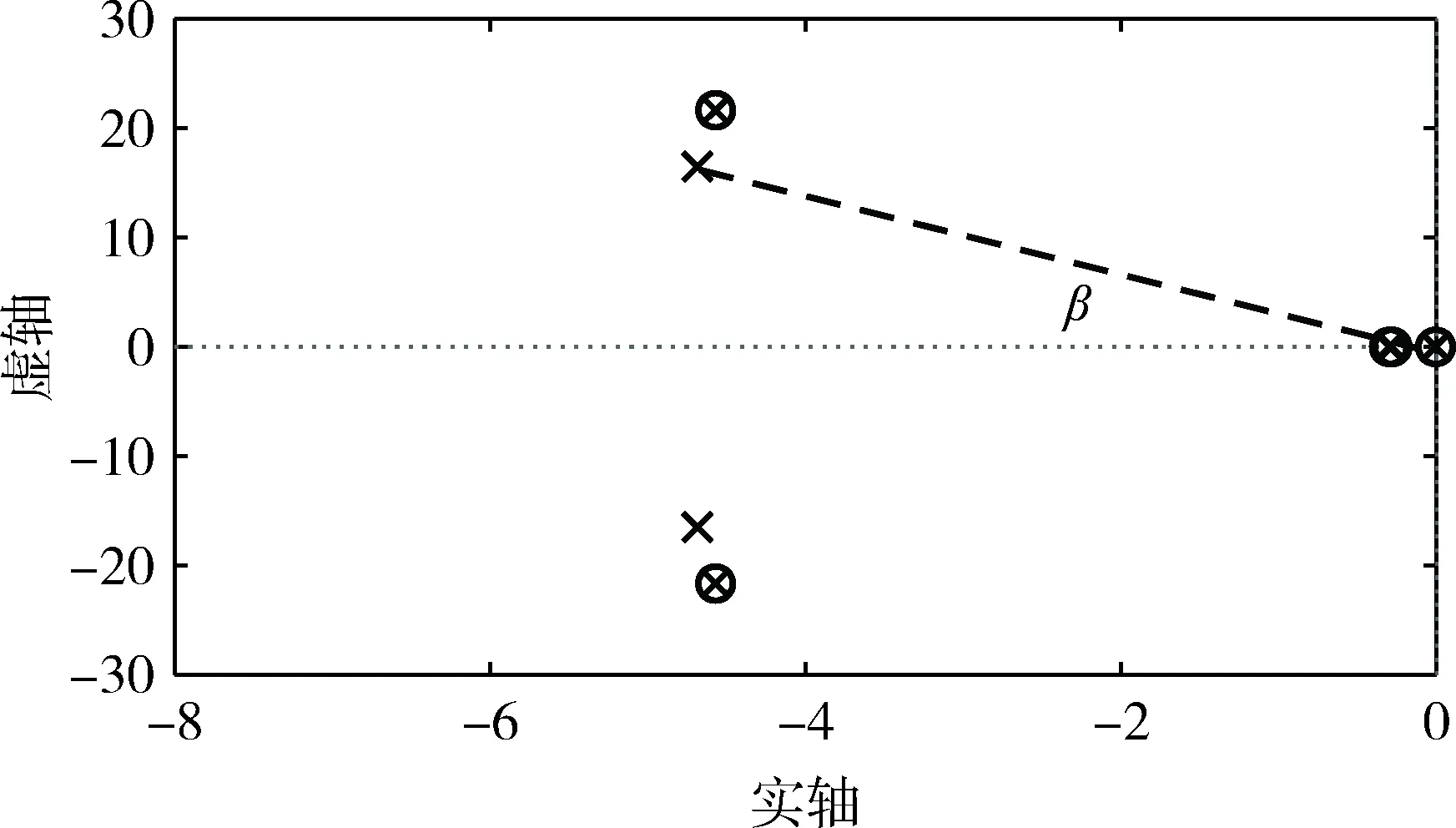
图5 优化前平动控制系统闭环零、极点分布图Fig.5 Closed-loop zero and pole distribution of translation control system before optimization
控制器优化后平动控制系统闭环零、极点分布如图6所示.可知,在控制器优化后,系统增加了一对偶极子、一个闭环零点和一个闭环极点.因新增零、极点到虚轴的距离超过闭环主导极点到虚轴距离的3倍,其对系统的影响可忽略,系统仍可近似为二阶欠阻尼系统.系统的闭环主导极点变为(-6.92,±17.1j),系统阻尼比ξt=0.38.
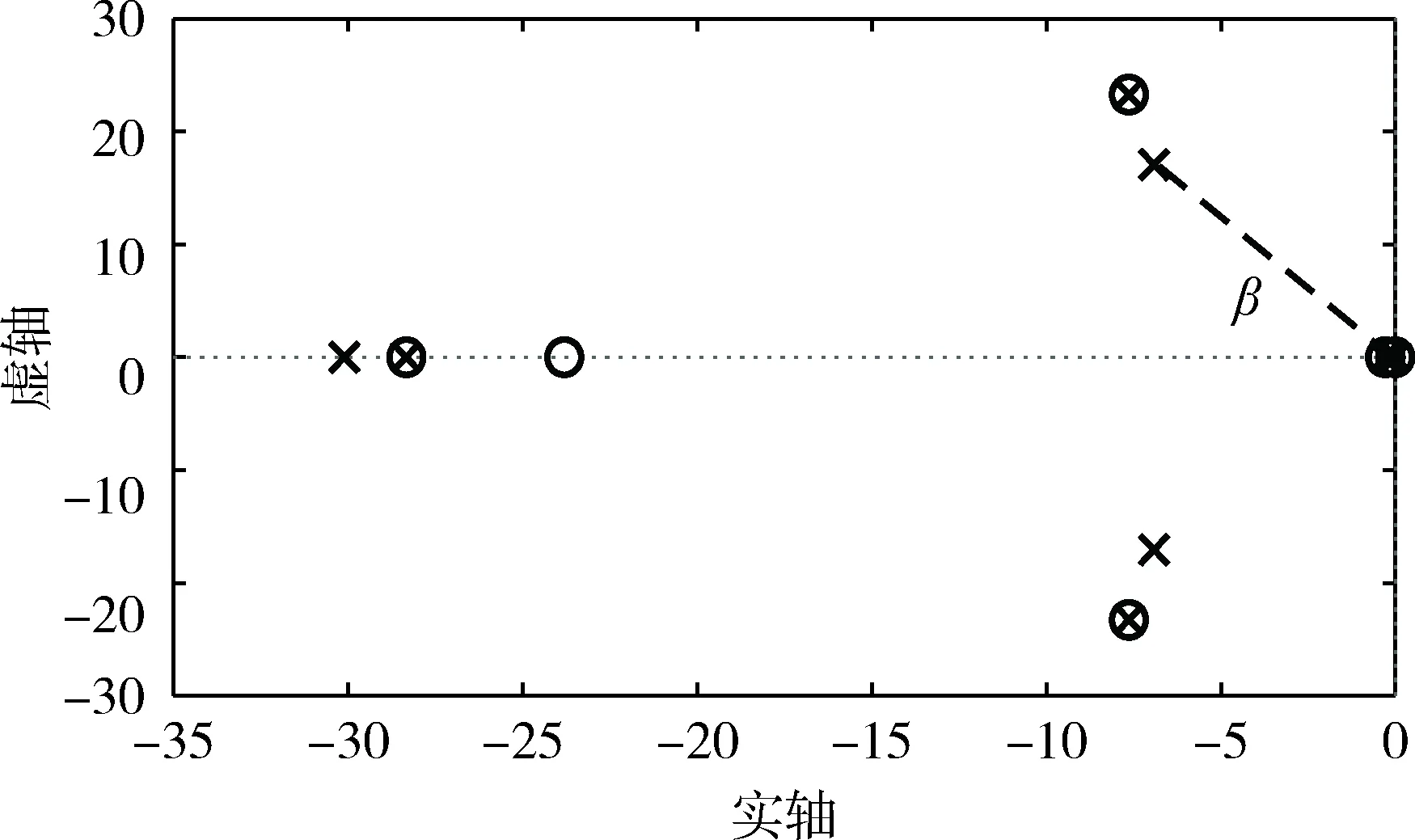
图6 优化后平动控制系统闭环零、极点分布图Fig.6 Closed-loop zero and pole distribution of translation control system after optimization
对比图5和图6可知,控制器优化可使平动控制系统闭环主导极点左移,系统阻尼比增大40%,有效增强了系统动态性能.且因平动控制系统所有闭环零、极点均位于虚轴左侧,系统闭环稳定.
同理,控制器优化前,转动控制系统闭环主导极点(-4.57,±21.63j),通过控制器优化左移为(-7.64,±23.3j).系统阻尼比ξr由0.21增至0.31,增幅超过47%,使转动控制系统的稳定性和动态性能获得较大提升.
4 仿真分析
4.1 控制系统BODE图
通过系统仿真,得到控制器优化前、后转动控制系统闭环BODE图如图7所示,获得系统性能参数如表2所示.
由图7和表2可知,控制器优化前,系统在3.5 Hz处激发控制模态,且谐振峰值较大,易引起系统的超调和振荡.通过控制器优化,谐振峰值减小,且系统在控制模态附近相角明显提升,增大了系统阻尼,提升系统的动态性能.

图7 控制器优化前后系统闭环BODE图Fig.7 Closed-loop BODE diagram of the system before and after controller optimization

表2 控制系统性能参数Tab.2 Performance parameters of the control system
4.2 阶跃信号仿真
将上平台转子的转动z方向系统给定(即图4中转角给定)设为阶跃信号,通过阶跃响应测试系统的稳定性和动态性能.系统仿真时控制指令为:第1 s时,将转子z轴期望姿态角设为40″并保持.仿真测得解耦控制系统在控制器优化前和优化后的阶跃响应为:

图8 控制器优化前后系统阶跃响应仿真曲线Fig.8 Simulation curves of the step response of the system before and after controller optimization
可知,通过控制器优化设计,可有效减弱系统振荡,缩短调节时间,提升系统的动态性能.因仿真为理想情况,无噪声干扰,所以z轴姿态角在阶跃响应后较快稳定在40″.
5 实验验证
为检验建立旋转关节仿真模型的准确性和控制算法的有效性,验证提出的控制器优化方法能否提高实际系统的控制性能,在已搭建的洛伦兹力磁悬浮旋转关节实验平台上进行验证.实验中的控制参数,控制指令,采样时间等与仿真条件完全相同.
第1 s时输出控制指令,将转子z轴姿态角设为40″(图4中转角给定)并保持,实验测得解耦控制系统在控制器优化前和优化后的阶跃响应如图11所示,从图中可获得各项动态性能指标如表3.
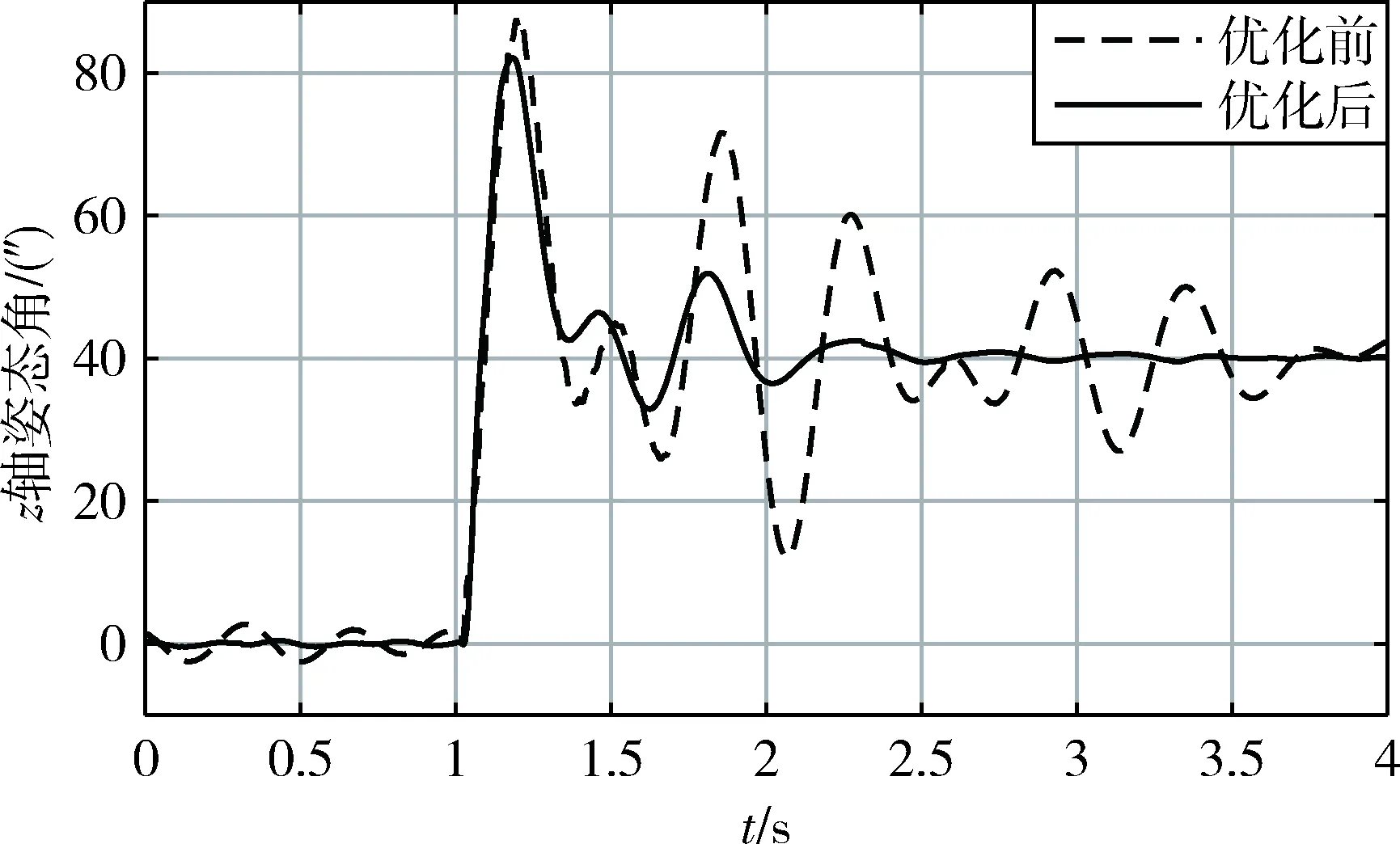
图9 控制器优化前、后系统阶跃响应实验曲线Fig.9 Experimental curves of system step response before and after controller optimization
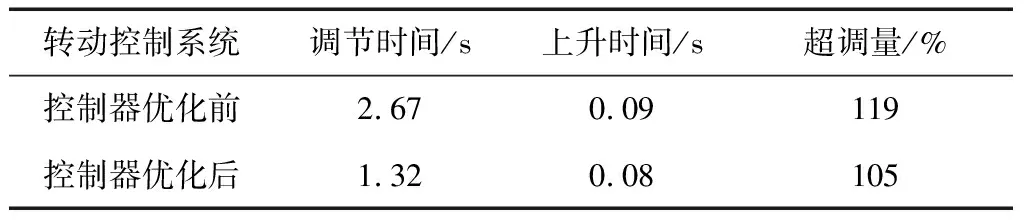
表3 阶跃实验动态性能指标Tab.3 Dynamic performance index of step experiment
由响应曲线和性能指标可看出,增加相位补偿器后,系统阻尼增大,系统振荡明显减弱,平稳性增强.同时,系统上升时间小幅减小,且调节时间减半,即阻尼增大的同时系统响应速度也有所提升,说明系统的快速性和平稳性得到综合优化,动态性能提升明显.
由图8和图9对比可知,控制器优化后仿真系统的上升时间trf=0.077 s,实验平台测得的上升时间trs=0.08 s,说明仿真系统和实验系统的控制带宽基本一致,验证了旋转关节仿真模型的准确性.
6 结 论
针对洛伦兹力磁悬浮旋转关节进行建模,设计解耦控制系统对上平台转子的平动和转动分别进行控制,使控制参数物理意义明确,便于调节,并通过控制器优化提升系统性能.通过仿真分析和实验验证,得到以下结论:
1)基于实验平台物理参数的模型仿真表明:解耦控制系统稳定且完全能控,通过增加相位补偿器完成控制器优化,可使系统闭环主导极点左移,在低频段内增大系统阻尼,减小系统超调,提升系统稳定性和动态性能.
2)基于仿真模型控制参数的实验结果表明:控制器优化方法使系统超调减小,振荡得到明显抑制,调节时间大幅减少,控制系统的快速性和平稳性得到明显提升.且仿真结果与实验结果基本一致,验证了旋转关节仿真模型的准确性.
