基于复合陷波器的磁悬浮飞轮微振动力抑制*

曾 塬 刘 昆 魏静波

中山大学航空航天学院，广州 510275

0 引言

航天器活动部件中飞轮是姿态控制的常用动力部件，也是航天器微振动的主要产生源，微振动会对航天器的成像质量和指向精度等关键性能产生较大影响，磁悬浮飞轮因具有无摩擦、阻尼可调以及可进行主动振动控制等优点越来越受到学者的关注，国内外学者对飞轮的振动机理及动力学建模进行了研究并取得了一系列成果[1-4]。

磁悬浮飞轮转子在加工制造时可以进行动平衡调整，但是不平衡质量仍然无法全部消除，因此飞轮转子在高速旋转时会产生不平衡振动，同时由于加工及材质不均的影响，磁悬浮轴承中位移传感器测量时会产生同频及倍频振动[5]。刘彬等[6]提出一种开环轴承力补偿的磁悬浮飞轮不平衡振动控制方法，该方法通过补偿位移刚度力达到控制不平衡振动力。魏彤等[7]提出一种位移刚度力超前前馈补偿的控制方法，消除同频电流后，再采用前馈对同频位移刚度力进行补偿；以上都是采用消除同频电流补偿位移刚度力进行振动力的控制，而直接以振动力或者力矩为控制目标的研究较少。崔培玲[8]等通过相移陷波器在全频内对不平衡振动产生的振动力进行了抑制研究。刘强[9]等将不平衡振动产生的约束力和惯性轴与几何轴不重合引起的离心力进行前馈，有效抑制了不平衡振动产生的径向振动。彭聪等[10]提出一种二阶陷波器控制方法，即在高低不同速度时采用陷波器交叉进行同频振动控制，取得较好的同频电流振动力控制效果，并对频率变化的同频振动力的抑制进行了研究[11]，但研究对象仅为质量不平衡产生的同频振动力，没有同时考虑除位移传感器等干扰产生的倍频振动力。

崔培玲等[2,12]主要采用重复控制方法，对磁悬浮飞轮系统同频及倍频电流进行了控制研究。通过电流控制了磁悬浮飞轮的微振动，没有抑制位移刚度力，且采用的重复控制方法因计算量大，收敛速度受到一定限制。

本文提出一种复合陷波器控制方法，通过直接构造同频振动力，控制由质量不平衡及传感器干扰产生的同频振动力，同时为提高控制精度，基于级联陷波器对传感器干扰产生的倍频电磁力进行抑制，达到抑制不平衡及传感器干扰产生振动力的目的。仿真研究验证了该复合控制方法的有效性。

1 磁悬浮飞轮干扰系统建模及分析

磁悬浮飞轮模型如图1所示，该飞轮为两自由度主动磁轴承，图中三自由度通过永磁体磁力进行被动稳定，飞轮转子绕飞轮定子旋转，本文主要研究两径向自由度的主动控制[13]。

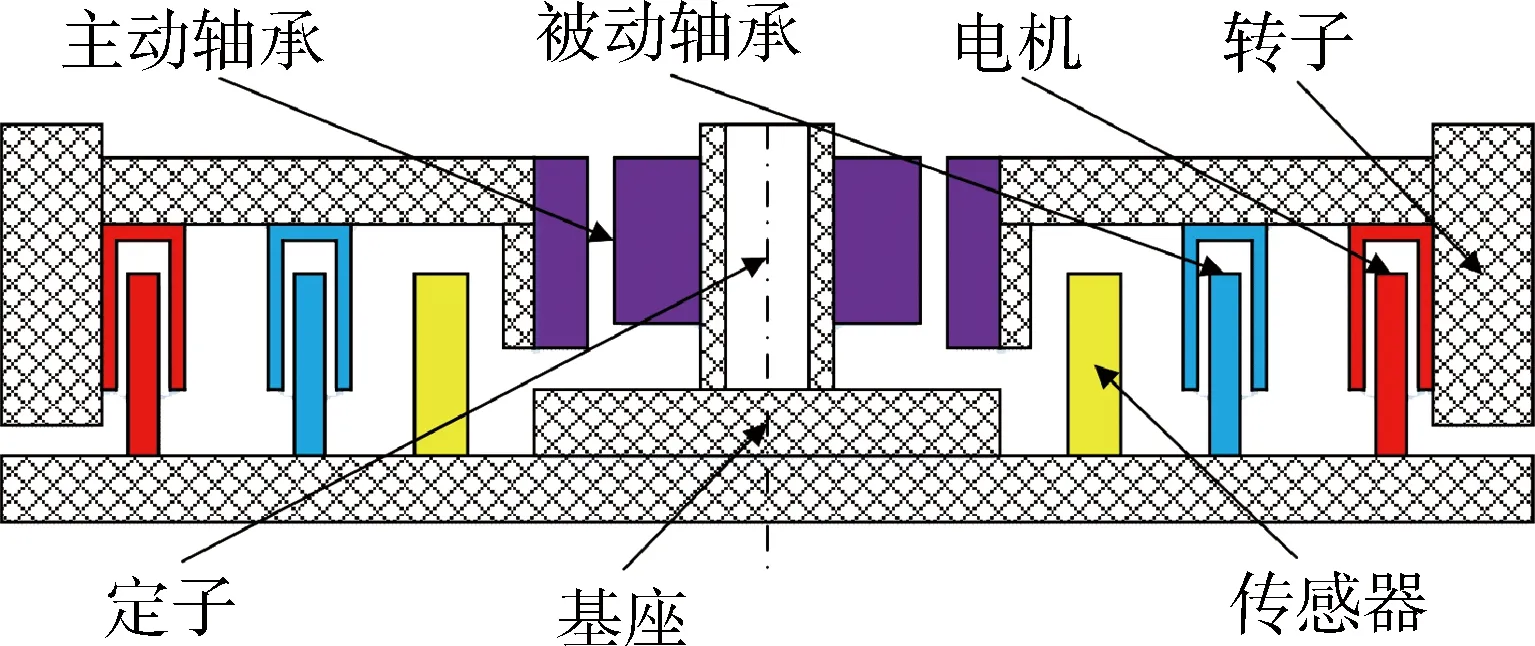
图1 两自由度主动磁悬浮飞轮

根据牛顿第二定律，两径向自由度运动方程可表示为：

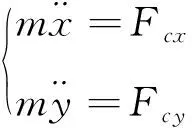
(1)

其中m为转子质量，Fcx为x方向合力，Fcy为y方向合力。考虑到x方向和y方向的对称性，为研究方便，以x方向为例进行分析；对磁悬浮系统中电磁力在平衡点进行线性化，并考虑不平衡质量振动时，动力学方向如下：

(2)

其中，Kh和Ki分别表示位移刚度系数和电流刚度系数，其中fd为不平衡力，Ω为转速，e为不平衡参数，φ为初始角，则fd可表示为

fd=meΩ2cos(Ω+φ)

(3)

而位移传感器干扰可以表示如下[14]

(4)

其中n为谐波阶次，esr为传感器干扰系数，θ为初始角。

根据动力学方程系统的控制框图如图2所示

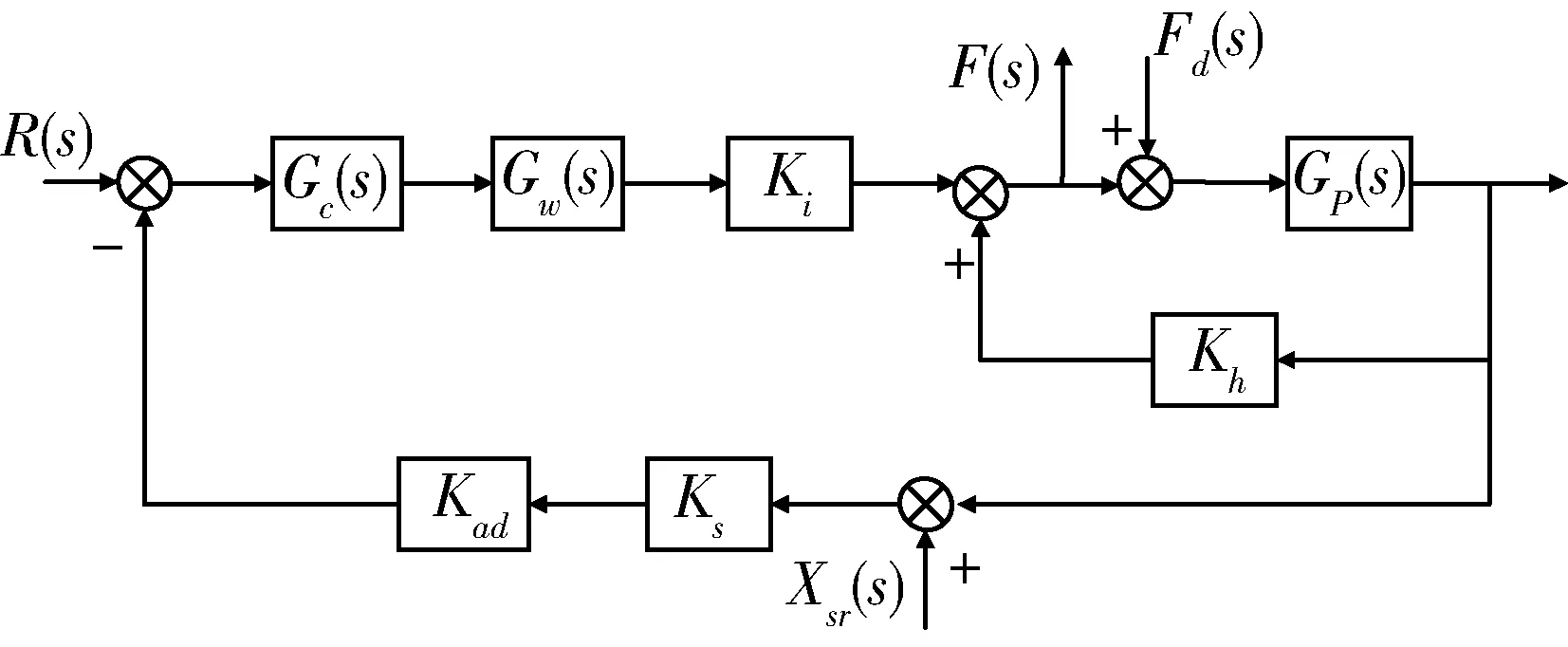
图2 x方向控制框图

根据控制框图，分别以Fd(s)和Xsr(s)为输入，F(s)为输出求出其传递函数为：

F(s)=Gd(s)·Fd(s)+Gsr(s)·Xsr(s)=
S(s)[(KhGp(s)-KadKsKiGw(s)Gc(s)Gp(s))Fd-
KadKiKsGw(s)Gc(s)Xsr1(s)]-
S(s)KadKiKsGw(s)Gc(s)Xsr2(s)

(5)

则振动力可以表示为同频量Fs(s)和倍频量Fm(s)之和

F(s)=Fs(s)+Fm(s)

(6)

Fs(s)=S(s)[(KhGp(s)-
KadKsKiGw(s)Gc(s)Gp(s))Fd-
KadKiKsGw(s)Gc(s)Xsr1(s)]

(7)

Fm(s)=-S(s)KadKiKsGw(s)Gc(s)Xsr2(s)

(8)

其中S(s)为

(9)

Xsr1和Xsr2分别表示传感器干扰的同频和倍频量，通过式(7)和式(8)可知，不平衡质量只产生同频振动力，即电流刚度力和位移刚度力，而位移传感器既可以产生同频力又可以产生倍频力，其主要通过传感器反馈进入系统，进入控制器产生电流刚度力。

2 磁悬浮飞轮干扰系统建模及分析

2.1 基于复合陷波器的抑制原理

为抑制同频力，以同频力为输入，通过陷波器将同频振动力负反馈至控制器，达到抑制同频振动力的目的，同时设计级联陷波器串联在控制器处，从而抑制传感器干扰产生的倍频电流刚度振动力，进一步抑制微振动力，提高抑制精度；复合陷波器控制框图如图3虚线所示。

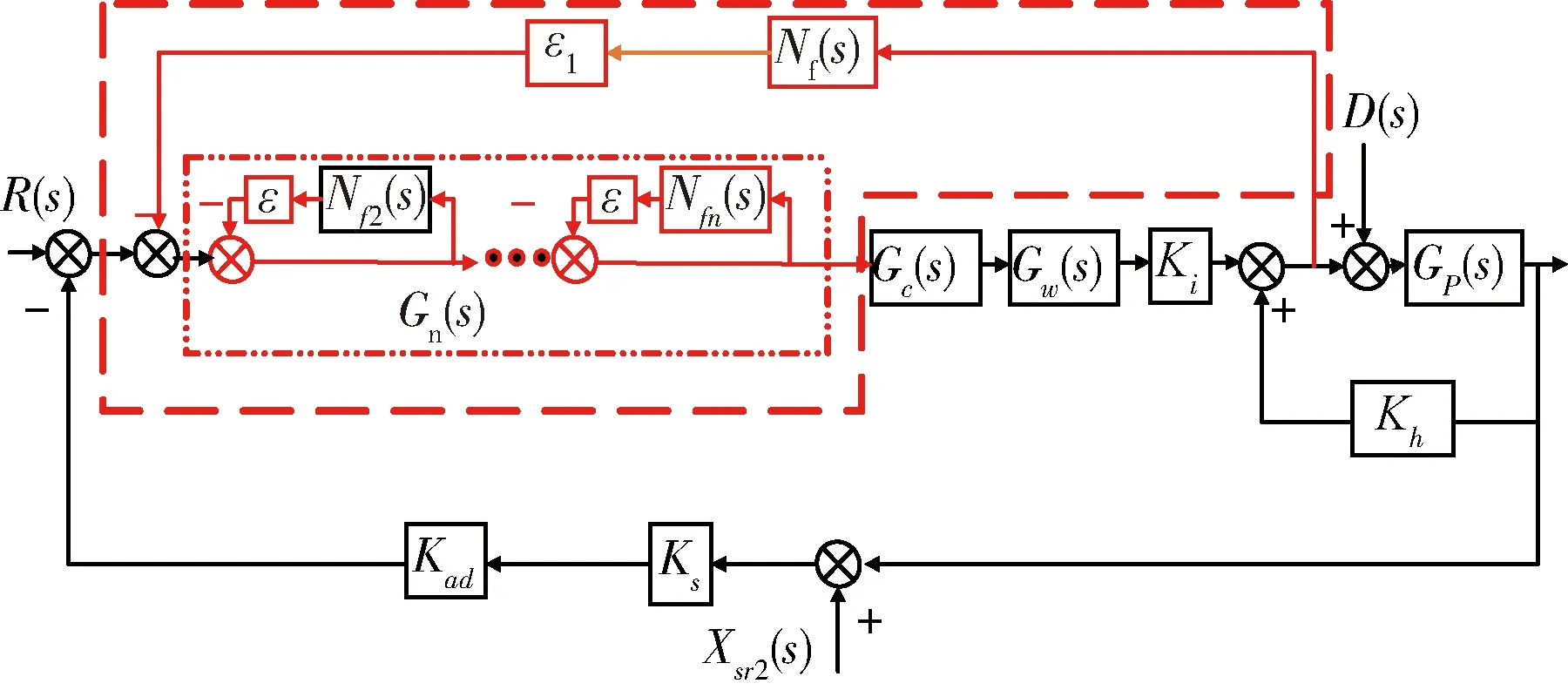
图3 复合陷波器控制框图

其中，D(s)为同频等效干扰力，可表示为

D(s)=Fd(s)-Xer1KadKsKiGc(s)Gw(s)/
[(1-Gp(s)Kh]

Nf(s)为同频滤波器，将构造的电磁力同频量进行滤波增益ε1倍后负反馈至控制器，构成同频陷波器[15]，其传递函数可表示为

(10)

其中TR和TJ为加权矩阵参数，用来确保闭环系统的稳定。

控制框图中Gn(s)为级联陷波器，其由n个倍频滤波器负反馈至回路后进行串联连接，从而进行多频电流电磁力的抑制。

Gn(s)的传递函数可表示为

(11)

其中TR2TJ2…TRnTJn分别表示各阶次选择器的加权矩阵参数，用来确保闭环系统的稳定。

根据控制框图，记GB(s)=Gc(s)Gw(s)Ki，分别以D(s)和Xsr2(s)中为输入，F(s)为输出求出其传递函数为：

(12)

根据式(10)可知

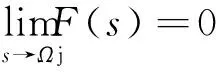
以Xsr2(s)为输入，F(s)为输出求出其传递函数为：

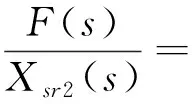
(13)

根据式(11)可知:

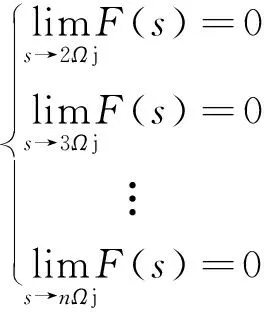
(14)

通过上述分析可知，复合陷波器可以完全抑制不平衡及传感器干扰产生的微振动力。

2.2 复合陷波器的设计及分析

根据实验室飞轮的振动频谱分析结果可知，该实验对象主要存在同频及5倍频的振动，因此在下述复合陷波器的设计中，Gn(s)以5倍频为例进行设计及分析。

2.2.1 多频陷波器Gn(s)的设计

为设计方便，采取分步法进行复合陷波器的设计，即设计Gn(s)时暂不考虑同频陷波Nf(s)，加入Gn(s)陷波器后，则系统以倍频量Xsr2(s)为输入，F(s)为输出，其闭环传递函数为

(15)

上式可改写为

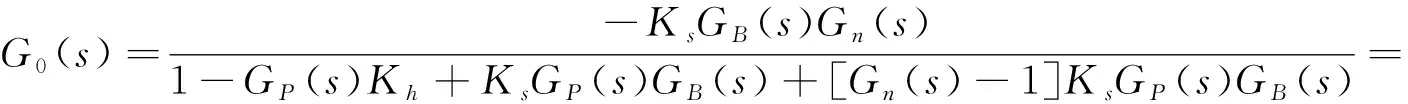
(16)

其中

(17)

(18)

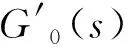
(19)

由上式可知，当ε5=0时，s=±5Ωj为该特征方程的根，为使系统稳定，其特征根分布在左半平面，以ε5为自变量对s求偏导得

(20)

其幅角满足如下条件，则可以使其特征根分布在左半平面

(21)

即TR5,TJ5满足如下不等式时系统稳定：

(22)

2.2.2 同频陷波器Nf的设计

完成Gn(s)的设计后，进行同频陷波器Nf的设计，同理将式(12)改写，得到系统的稳定所需特征方程为

s2+Ω2+ε(TRs-ΩTJ)S′(s)=0

(23)

(24)

S′(s)为前述设计所得包含Gn(s)的稳定系统。

同理根据根轨迹出射角要求，为使系统稳定，TR和TJ须满足

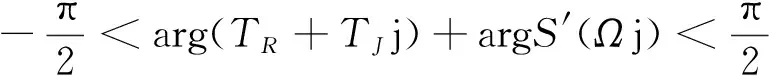
(25)

3 仿真校验

为校验上述控制方法的抑制效果，采用MATLAB/Simulink进行仿真分析研究，飞轮磁悬浮转子系统的仿真参数见表1。

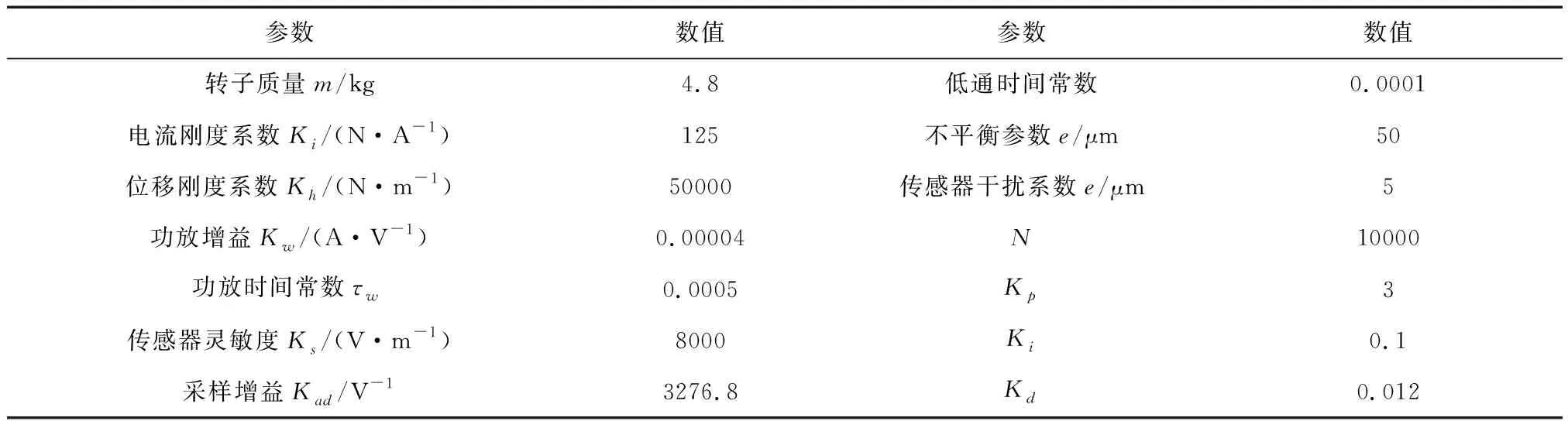
表1 磁悬浮飞轮参数

根据表1中转子系统各参数绘制式(18)的相频特征曲线如图4所示，为使得控制系统稳定，需满足式(22)，根据图中给出的不同转速时的相位角变化，为使系统在全频内保持稳定，设定ε5=2,T5R和T5J取值如下

图4 式(18)相频特征曲线

(26)

式(24)中S′(s)含有Gn(s)，分别绘制转速Ω=100rad/s，Ω=500rad/s时S′(s)的幅相频特征曲线如图5所示，由其幅频特征曲线可知，由于Gn(s)的存在，在5倍转速处幅值具有较好的抑制值，其相位角的范围为(-80°，180°)，为使系统稳定,需满足式(25)，TR和TJ可取如下值:

图5 不同转速下式(24)幅频相频特征曲线

(27)

考虑质量不平衡及传感器干扰，分别在转速209rad/s和628rad/s下进行仿真研究。当采用TR=-200，TJ=-10时，转速为628rad/s时系统失稳，说明此时需改变参数补偿其相角；而采用TR=100，TJ=-10后系统稳定，补偿后仿真系统稳定。仿真结果分别如图6和图7所示。按照式(26)参数进行仿真时，系统在高速仍然可以保持稳定，验证了在全频工作范围内保持系统稳定的可行性。

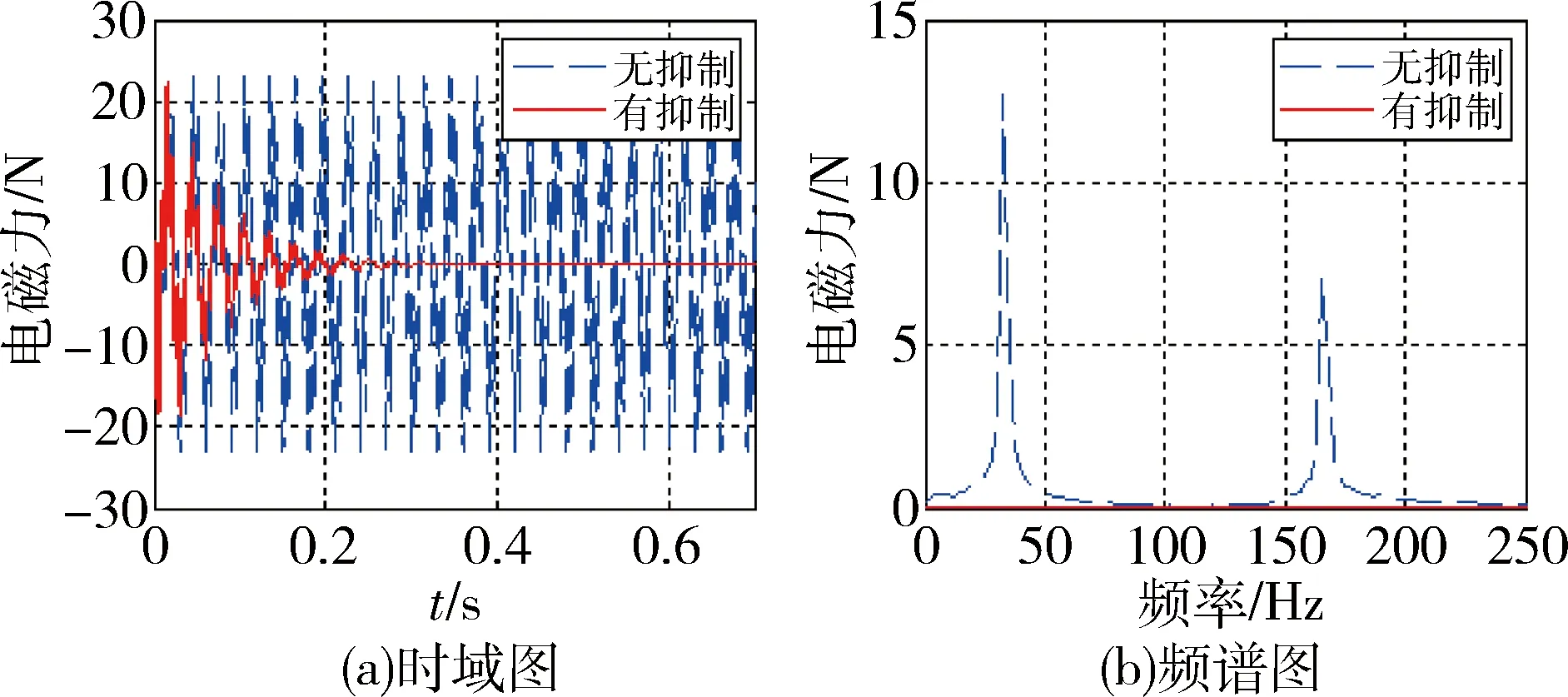
图6 有无抑制对比(转速209rad/s)

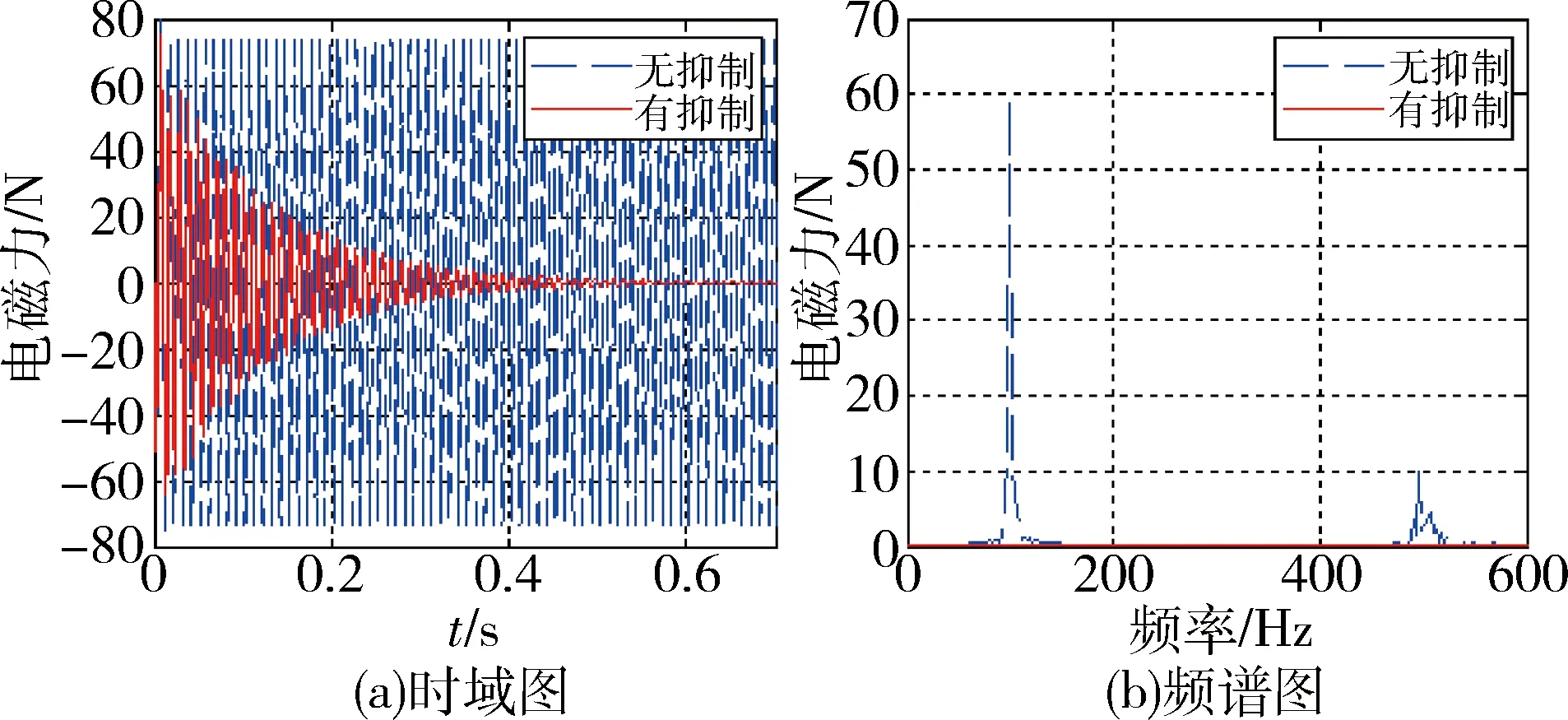
图7 有无抑制对比(转速628rad/s)

在未采用主动振动控制时，系统振动力时域变化如图6(a)和图7(a)，电磁力因质量不平衡及传感器干扰产生较大振动，特别是在转速较高时，振动力较大，在转速209rad/s和628rad/s时，其同频振动力幅值分别达到13.5N和58N, 电磁力振动会对磁悬浮飞轮的工作效果产生不利影响。为了抑制振动力，采用复合陷波器进行控制，仿真结果如图6(b)和图7(b)所示，同频振动和倍频振动都得到了抑制；从时域图可以看出，转速为209rad/s的系统在0.3s时，其值趋近为0N，转速为628rad/s的系统在0.65s时，其值也趋近为0N，说明干扰产生的振动力能很快被完全抑制。

4 结论

通过建立磁悬浮飞轮受干扰模型，以振动力为研究对象，分析了同频及倍频振动力产生的机理，提出以同频振动力与倍频电流刚度力复合控制的微振动力控制方法，并在全频率工作范围下对复合陷波器进行了设计；采用MATLAB/Simulink仿真校验了转速在209rad/s和628rad/s时振动抑制情况，同频振动和倍频振动的幅值均趋近于0N，研究结果表明：在采用复合陷波器控制方法后，不平衡振动及传感器干扰产生的振动力得到了有效控制，验证了该方法的有效性；但是当系统存在多倍频率干扰时，复合陷波器的设计相对复杂，因此改进抑制多倍频的方法将是下一步值得研究的问题。