基于点云的空间非合作目标位姿测量方法研究

王昕宇 解永锋 陈 益 王国辉

1.北京宇航系统工程研究所，北京 100076 2.中国运载火箭技术研究院，北京 100076

0 引言

在轨服务与空间碎片清理是近年来各国关注的焦点[1]，作为其核心技术之一，近距离的空间非合作目标的位姿测量技术也被广泛研究[2-3]。根据非合作目标模型是否已知，分为已知模型和未知模型，对于已知模型的位姿测量，多采用模板匹配的方式[4-5]，已有大量研究较为成熟，而目前对未知模型的位姿测量的研究则充满挑战。

针对模型未知的空间非合作目标位姿测量，常用的解决方案为同时定位和建图(SLAM)。SLAM最早在机器人领域提出，它指的是：机器人从未知环境的未知地点出发，在运动过程中通过重复观测到的环境特征定位自身位置和姿态，再根据自身位置构建周围环境的增量式地图，从而达到同时定位和地图构建的目的。

文献[6]基于SLAM的贝叶斯滤波估计模型,提出了基于视觉的非合作目标的位姿测量方法，实现了对翻滚目标的位姿测量。文献[7]将经典视觉SLAM算法ORB-SLAM应用于空间非合作目标位姿测量，取得了较好的测量精度。文献[8]基于共线投影原理创立了双目视觉的测量模型，融合惯性元件进行组合导航。然而空间光环境复杂且变化剧烈，纯视觉方法应用受限。激光雷达作为主动式传感器，具有较好的光照不变性，被航天器广泛应用[9]。因此基于激光雷达的位姿测量技术被越来越多的学者重视。

文献[10]以迭代最近点(ICP)算法为基础，提出的考虑累积误差的参数传递法进行序列点云配准。文献[11]分析了非合作目标相对位姿测量中的漂移问题，提出了基于位姿平均的漂移修正方法。文献[12]将2D-3D多特征融合，求解目标位姿。而文献[13]则利用位姿图优化技术，结合闭环检测，提出了解决累计误差的完整SLAM框架。

上述提到的点云配准多以Besl等人1992年提出的ICP算法为基础[14]。但面对非稠密点云，ICP的最近点匹配退化严重。文献[15]中扩展ICP算法整合了点与点和点与面的匹配，拓展了ICP算法适用范围。但ICP算法每次迭代均需搜索最近点，计算代价较高。文献[16]提出了NDT算法，通过匹配相邻帧正态分布栅格，无需迭代搜索最近点，效率更高。

LOAM算法[17]为提高实时性，采用提取边缘点和平面点匹配的方式，减少了待匹配点数量，同时为了降低运动拖影的干扰，里程计与建图分为了高频和低频2部分。针对低成本的固态激光雷达单线收发、不规则采样的特点，Livox_LOAM[18]基于LOAM增加了坏点剔除和分段匹配的步骤，提高了里程计的鲁棒性。本文在此基础上，结合空间非合作目标的特点，改进了特征点选择和位姿迭代优化流程，提出了一种适用于固态激光雷达的空间非合作目标位姿测量方案。

1 特征点提取

1.1 点云采样

本文主要研究基于固态激光雷达位姿估计，下面以livox公司推出的mid-40激光雷达为例说明点云的采样特点。

如图1(a)和(b)所示，激光雷达采用单线激光束在一个圆形平面内扫描，形成一个夹角38.4°的锥形扫描视野。扫描轨迹如图2所示，形状类似花瓣。为增加视场内的扫描点覆盖率，该激光雷达采用了非重复扫描模式，扫描花瓣在不断旋转。不过这也使得以搜索最近点为核心的ICP算法效果大打折扣。

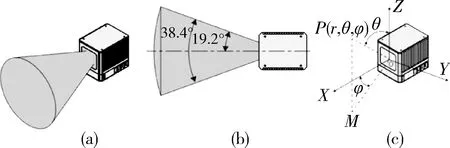
图1 mid-40激光雷达有效视场范围

图2 mid-40激光雷达扫描轨迹

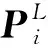
(1)

1.2 边缘点提取

为了计算每帧点云本地坐标系到世界坐标系的转换(即位姿)，采用特征点匹配的方式，下面详细介绍如何针对空间非合作目标提取特征点。

1)转折点

激光雷达在以花瓣状轨迹扫描过程中，得到的序列点在遇到物体边缘时会出现转折，体现在点云坐标上则为相邻点之间的微分向量夹角增大。

(2)

式(2)计算出某点Pi和前后两点之间向量的夹角，以此作为转折点的判断标准。但需注意以下2点：

a.剔除视野边缘点。由图2知，扫描花瓣在视野中央，轨迹接近直线，而在视野边缘有近180°转变，这将影响式(1)的判断。因此将距x轴15°外的点均不作转折点判断。由于一般将目标航天器锁定在视野中央，因此不会明显降低特征点数量。

b.距离雷达近优先。图3(a)中，A、B两点均可由式(1)判断为转折点，而显然点A是由于点B的遮挡而转折，更换视角后，点A将不再是边缘点，因此在检测到转折点后需判断当前点与下一个点哪一个距离雷达更近，将更近点选为边缘点。

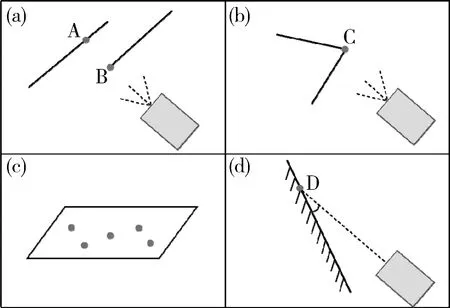
图3 激光雷达采样点示例

2)断点

在空间环境中，如果激光束没有照射到目标航天器上，则意味着无法被反射回雷达，测量结果为无穷远。而激光雷达扫描中从航天器到宇宙空间过程中必然经过边缘点，本文称之为断点，如图3(b)所示。因此如果某点的一侧为无穷远，而该点在另一侧连续，则可以为是断点。

1.3 平面点提取

判断某一点是否在一个平面上，很难通过单线扫描的序列点完成，本文借鉴主成分分析算法，提出一种单线扫描下的平面点提取方案，步骤如下：

a.选择待判断点附近一定距离内点(如5 cm内)，假设为k个，由图2可知，0.1s时扫描覆盖率已经较高，因此k个点不会来自共线的连续扫描。

b.计算k个点的均值与协方差矩阵，并计算协方差矩阵的特征值与特征向量。

c.根据主成分分析理论，协方差矩阵的特征值越小，在该特征方向的分布越集中，近似压缩在一个平面上，如图3 (c)所示。因此将最小特征值是次小的三分之一作为k个点是否组成平面的依据，并据此判断该点是否在平面上，即平面点。

然而，值得注意的是，图3(d)中平面与激光束夹角很小，此时激光束会在平面上照射出拉长的光斑，测距精度将显著下降，因此对该种情况的平面点进行剔除。

2 迭代位姿优化

为解算出激光雷达绕空间目标移动过程中的位姿变化，需要计算每一帧本地坐标系下的点云相对于第一帧的世界坐标系之间的旋转和平移，即(Ri,Ti)。本文采用上一节介绍的算法提取每一帧的特征点，将其与之前所有帧的特征点进行匹配，迭代优化Ri与Ti使得匹配误差最小。

2.1 特征点匹配

由于固态激光雷达的不重复扫描特点，直接点与点的匹配很难实现，因此采用边缘特征点与直线和平面特征点与平面的匹配方式。

为提高迭代效率，设置合适位姿初值，本文以i-1与i-2帧间位姿变化预估第i帧位姿，在齐次坐标系下表示为：

(3)

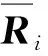
1)点与线

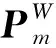
(4)

图4 匹配误差示意图

2)点与面

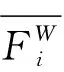
(5)

2.2 迭代优化

2.1节分别计算出点与线、点与面匹配的误差，一帧点云总的误差为

(6)

图5 位姿优化算法流程

图5的算法流程中，特征点匹配完成后，增加一步误差加权：

(7)

式中：d为误差值，ρ(d)为加权系数，h为给定参数，设为0.01m。经过该步骤，匹配误差较大项在总误差中占比会下降，减少了离群点对最终结果的影响。

算法最后判断优化是否结束，若前后两轮优化结果差别很小或达到最大轮次，则结束优化，输出结果。否则算法将以最新的估计位姿(Ri,Ti)更新特征点在世界坐标系中的坐标，迭代优化。

2.3 运动补偿

固态激光雷达单线扫描特点，导致同一帧点云并非同时采样获得，而是在一个时间段内依次采样，而采样时雷达自身在不断运动，由此产生运动拖影，本文采用线性插值方法进行运动补偿。

以(Ri,Ti)为第i帧最后一个采样点的雷达位姿，则第i帧最后一点(时刻ti)到第i-1帧最后一点(时刻ti-1)之间的位姿变换为：

(8)

(9)

式中：旋转角θ可由ΔRi的迹计算，而旋转向量经ΔRi的旋转不会改变，所以旋转向量n为ΔRi的特征值为1的特征向量。旋转角线性插值后使用罗德里格斯公式[19]转换回矩阵：

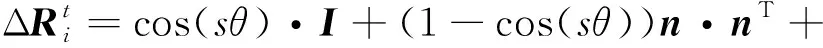
(10)

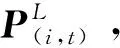
(11)

3 实验校验

为了校验所提算法的有效性，本文对气浮台半实物实验所得数据进行处理。

3.1 实验条件

为模拟太空中追踪航天器与目标航天器的真实相对运动情况，采用了气浮模拟器绕飞目标模拟器的方式进行演示实验，如图6所示。

图6 实验装置

追踪模拟器距离目标模拟器2m，以1.5(°)/s的角速度绕飞。追踪模拟器上安装有光学追踪器，使用OptiTrack外部光学测量系统测量位姿，将其测量值作为算法参考的位姿真值。

3.2 结果及分析

追踪模拟器绕飞目标模拟器一周后，根据计算得到的每一帧点云位姿，将点云坐标统一变换到世界坐标系下，得到图7的目标三维模型。

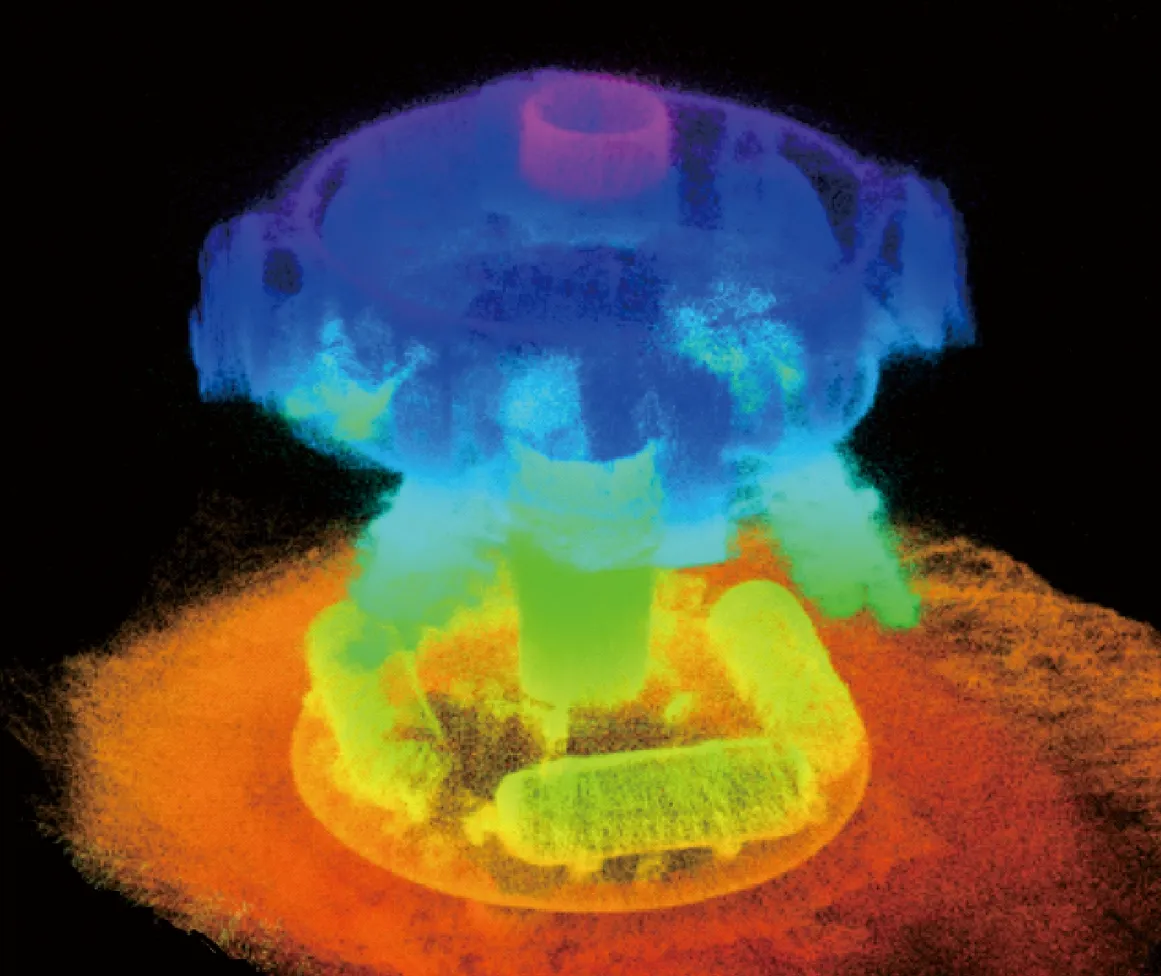
图7 目标模拟器三维模型

图8为追踪模拟器的绕飞轨迹误差热力图，图9展示了三轴坐标系下激光雷达测量轨迹与真实轨迹的误差，图中可知，两条轨迹基本吻合。图10量化统计了测量轨迹与真实轨迹的累积误差，即图中APE。绝对累积误差并未持续增加而是上下震荡，表明算法中每一帧点云均和全局地图匹配的设计，有一定的回环修正能力。

图8 测量轨迹误差热力图

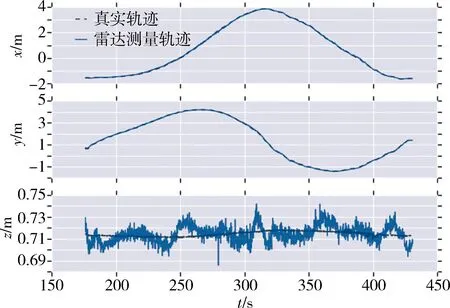
图9 三轴坐标系下轨迹误差

图10 绝对轨迹误差信息

本文将所提出算法与Livox公司开源算法对比，结果如表1所示。在最大误差相似情况下，本文算法的轨迹均值误差与均方根误差均明显低于对照算法，能够满足航天器相对位姿测量的要求。

表1 算法轨迹误差对比

4 结论

为测量模型未知的空间非合作目标位姿，本文提出了基于固态激光雷达的测量方法。该方法针对空间目标提取特征点，与全局地图匹配后迭代优化位姿，克服了固态激光雷达不规则采样的缺点，在半实物实验中准确测量了相对位姿变化，证明了方法的有效性。