一种防空装备全被动作战定位方法
2022-08-02张梦骏蔺红明
刘 博 张梦骏 付 磊 高 雅 蔺红明
上海机电工程研究所,上海 201109
0 引言
防空装备全被动作战是指系统在不向外辐射电磁波、激光等能量的情况下完成对目标的搜索跟踪及打击拦截。随着电磁干扰技术、精确打击技术的快速发展[1],传统防空装备以雷达等有辐射信号设备为主要探测、制导手段的作战方式已无法适应当前复杂的战场环境。面对反辐射导弹以及电磁干扰的威胁,采用光电设备进行探测、制导的全被动作战样式,可以有效提升防空装备在电子战中的作战能力及效果。
光电探测设备通过目标辐射热或者可见光实现对目标的搜索跟踪,不受电磁干扰影响,不向外辐射能量,极大提升了武器装备的隐蔽性。同时光电探测设备还具有测角精度高、目标识别能力强的优点,在探测低空目标时,不受地杂波影响,不存在多路径效应[2]。
行进间作战技术可以进一步提升防空装备武器系统作战性能,实现武器装备快速、机动作战,极大提高了系统自身的生存能力,还能为机械化部队提供不间断的伴随防空能力,提升防空装备性能。
在全被动行进间作战时,防空装备一般采用单车作战,且光电探测设备只能测量目标角度信息,无法获取目标的距离信息,如何通过单光电设备探测的纯角度信息对目标进行快速、精确的定位,是全被动作战的一项关键技术。
郑晟等对光电设备在防空武器系统中的应用进行了深入的分析和研究,证明了光电设备应用于防空武器装备的有效性[3],但是未能分析全被动作战场景;管旭军等利用UKF技术,改进无源定位算法,实现了纯角度信息下的目标快速定位[4],但是算法较为复杂。本文针对防空装备全被动行进间作战场景下的目标定位问题,基于单光电设备角度测量,提出了先采用α-β-γ滤波算法减小角度观测误差[5],再用递推最小二乘算法求出目标初始位置、目标速度,进而解算目标实时位置的方法[6]。仿真结果表明,递推最小二乘算法可有效对目标进行定位,采用α-β-γ滤波算法提前对角度滤波的方法可以提高目标定位算法的收敛速度,提高目标定位精度。
1 定位模型及算法原理
1.1 定位模型建立
图1所示为测量装备与目标之间的相对运动关系。以开始进行定位时测量装备的位置为坐标原点O,建立北天东地理坐标系,X轴为北向,Y轴垂直水平面向上,Z轴指向测量东。

图1 测量装备与目标相对运动关系示意图
其中:Kc为光电测试设备航向角,Vc为测试设备行驶速度,φc为测试设备行驶方向与水平面夹角)。针对匀速直线运动目标,Km为目标航向角,Vm为目标飞行速度,φm为目标俯冲角。在目标探测初始时刻(t1),光电测试设备与目标距离为l1,俯仰角为ε1,方位角为β1。在任意时刻tj,光电测试设备与目标距离记为lj,光电测试设备测得目标俯仰角为ε1,方位角为β1。
根据图1中目标相对运动关系,对空间几何封闭图形OO’M’M从X轴、Y轴和Z轴3个方向分别进行分析,可获得以下方程:
(1)
简化可得:
(2)
其中:Xcj为光电测试设备到tj时刻在X方向移动距离,Ycj为Y方向移动距离,Zcj为Z方向移动距离;Vmx=VmcosφmcosKm,Vmy=Vmsinφm,Vmz=VmcosφmsinKm。
1.2 定位算法原理

通过式(2)计算可得:
Vmztj[cosβj+sinβjsinεj]+Vmxtj[cosβjsinεj-sinβj]-
Vmytjcosεj+l1[cosε1sinεjcos(βj-β1)-
sinε1cosεj-cosε1sin(βj-β1)]=Zcj[cosβj+
sinβjsinεj]+Xcj[cosβjsinεj-sinβj]-Ycjcosεj
(3)
实际上,俯仰角ε1、方位角β1为测量值,存在测量误差,因此式(3)左右两边无法完全相等,tj时刻误差Δ(tj)可记为:
Δ(tj)=Vmztj[cosβj+sinβjsinεj]+
Vmxtj[cosβjsinεj-sinβj]-Vmytjcosεj+
l1[cosε1sinεjcos(βj-β1)-sinε1cosεj-
cosε1sin(βj-β1)]-Zcj[cosβj+sinβjsinεj]-
Xcj[cosβjsinεj-sinβj]+Ycjcosεj
(4)
根据t1,t2,…,tj观测值,构建目标极小化函数:
(5)
对极小化函数分别对Vmx,Vmy,Vmz和l1求偏导,并令结果为0,计算并简化可得:
(6)
其中:
Aj=tj(cosβj+sinβjsinεj);
Bj=tj(cosβjsinεj-sinβj);
Cj=-tjcosεj;
Dj=[cosε1sinεjcos(βj-β1)-sinε1cosεj-
cosε1sin(βj-β1)];
Fj=Zcj[cosβj+sinβjsinεj]-Xcj[cosβjsinεj-
sinβj]+Ycjcosεj。
令Xk=[VmzVmxVmyl1]T,式(6)可写为:
H(k)Xk=F(k)
(7)
其中:F(k)=[F1F2…Fk]T,
针对存在观测噪声的实际情况,采用递推最小二乘法解算式(7),可得递推公式为:
(8)
K(k)=P(k-1)H(k)[HT(k)P(k-1)H(k)]-1
(9)
P(k)=[I-K(k)HT(k)]P(k-1)
(10)
(11)
2 观测值预处理算法
采用递推最小二乘估计进行计算时,算法没有考虑估计量与观测量的统计性质,未根据观测值、估计值的统计信息对计算函数加以限制。在观测值测量误差较大的情况下,算法会产生较大误差,影响收敛速度,甚至产生发散。针对光电探测信息存在较大误差的情况,本文对测试值进行滤波预处理,减小探测方位、俯仰角的随机干扰误差,剔除大幅度毛刺,提高输入数据的正确性。
考虑到实际作战过程中运算的简便性、稳定性,采用α-β-γ滤波对观测的俯仰角ε1,方位角β1进行滤波平滑处理,减小光电设备的测量误差,剔除毛刺。α-β-γ滤波作为Kalman滤波的一个特例,由于不涉及矩阵计算,计算方法简单,数据计算量小,稳定性高,应用在多型防空武器设计中,显示滤波数据有较高的准确性[8]。
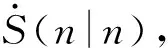
当n=1时,
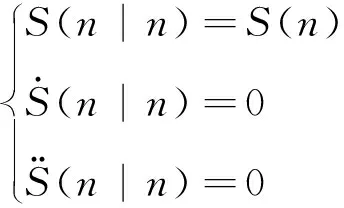
(12)
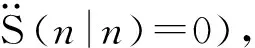
预测值为:
(13)
新息为:
ΔS(n)=S(n)-S(n|n-1)
(14)
滤波值为:
(15)
(16)
其中:Δt为前后两输入点对应时间差,Nw为观测点数,α(n),β(n)和γ(n)为增益系数。
假设标定的光电探测设备测量角度误差为δ,则当ΔS(n)>3δ时,认为S(n)为野值,令ΔS(n)=0。
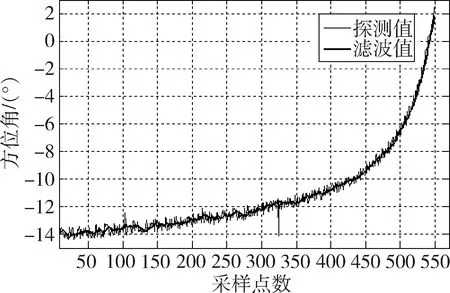
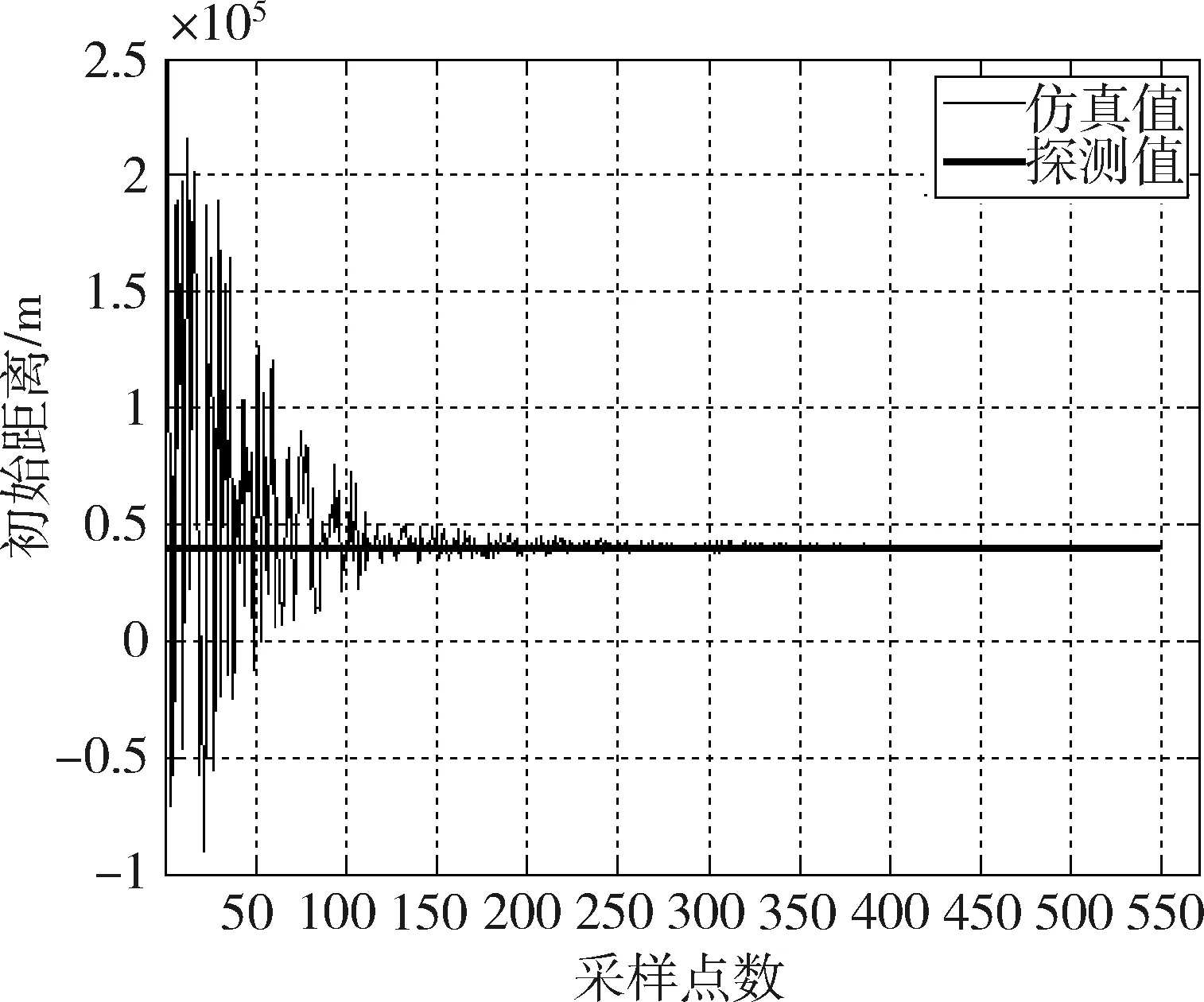
当n>Nw时,令n=Nw,计算方法与1 第1、2节分别对定位算法原理、观测值预处理算法进行了分析,结合防空作战装备实际作战过程,设计了采用单光电设备探测进行目标定位的算法流程,如图2所示。 图2 单光电设备被动定位解算流程 防空装备进入行进间作战,通过光电探测设备对目标进行搜索,发现目标后,将探测到的目标相对战车的方位角、俯仰角发送给指控系统,指控系统采用α-β-γ滤波算法,分别平滑方位角、俯仰角,剔除野值。对处理后的方位角、俯仰角采用最小二乘迭代算法进行解算,计算目标的初始距离及各方向速度,随后根据装备的初始位置、目标速度及时间,解算目标的当前位置,完成目标定位。指控系统根据目标信息解算各项所需要的参数。 采用本文提出的算法对数据进行仿真分析。仿真数据如下:探测器初始位置为(0,0,0)m,速度为(2,0,2)m/s,加速度为(0.1,0,0.1)m/s2;目标初始位置为(40000,8000,-10000)m,速度为(-330,-30,100)m/s,无加速度。探测器采样周期为0.5s,角度测量误差为0.5°。考虑到探测器实际跟踪目标过程中会出现不稳定情况,加上了一定量的干扰误差。 由图3所示,通过α-β-γ滤波处理探测器观测值,可以有效平滑观测数据,降低探测值的随机误差,对于添加的几个孤立的野值,也进行了有效剔除。 图3 目标方位角观测值及滤波值 图4为通过递推最小二乘算法解算的目标初始值,其中,图4(a)为对探测器观测方位角、俯仰角进行滤波后解算的目标初始值,图4(b)为未对观测值进行滤波处理时解算的目标初始值。 从图4(a)可以看出,采用递推最小二乘算法可以有效解算目标初始距离。随着观测点数不断增加积累,解算的目标距离与真实值越来越接近。当采样点达到250个点(125s)时,解算出的目标初始距离基本稳定,与实际距离的误差可以减小到10%以内,从而实现在全被动作战下对目标的定位。 同时,对比图4(a)与图4(b)可以发现,通过α-β-γ滤波对探测器观测值进行滤波,可以提高解算的目标初始值的收敛速度及解算精度,进一步提升作战能力。 图4 观测值滤波前及滤波后解算的目标初始距离 通过前面算法可以发现,通过递推最小二乘算法解算目标初始距离时,定位速度、定位准确度有所欠缺。在前面仿真条件基础上,只将探测器加速度(0.1,0,0.1)m/s2增加到(0.15,0,0.15)m/s2,再进行计算,图5为仿真结果数据,可以看到,解算的目标初始距离在收敛速度及收敛精度上都有一定程度的提高。 图5 增加探测器加速度后解算的目标初始距离 单站定位技术对防空装备全被动作战起着至关重要的作用[9]。本文通过理论推导,获得了递推最小二乘算法,通过仿真,发现该算法可有效解算目标初始距离,定位精度及定位速度能满足防空装备作战需求,且该算法简单,运算便捷,可为防空装备在行进间全被动作战提供有效支撑,具有较强的工程应用性。此外,本文采用α-β-γ滤波对探测器的探测值先进行滤波处理,可有效平滑探测数据,剔除毛刺,提升了递推最小二乘定位算法解算的精度及收敛速度。3 单光电设备被动定位方法

4 仿真试验与结果分析
4.1 观测值滤波处理
4.2 观测值滤波处理

4.3 其它
5 结束语
