GPS失锁时的RBF神经网络辅助组合导航算法*

赵乐宁 李 杰 冯凯强 魏晓凯

1.中北大学仪器与电子学院，太原 030051 2.中北大学仪器科学与动态测试教育部重点实验室，太原 030051

0 引言

随着以全球定位系统(GPS)为代表的导航应用产业发展越来越蓬勃，其应用环境条件也日趋困难复杂，由捷联惯性导航系统(SINS)和GPS所组成的高精度组合导航系统[1]在使用时受周边高压线、频率电台以及恶劣环境的干扰[2]或载体处于大机动运动的情况，导致组合导航系统中的GPS接收机信号失锁，系统变为纯惯导工作模式，即由SINS中的微惯性器件加速度计与陀螺仪提供位置信息。但单纯由SINS中的MEMS器件提供的信息随着时间积累，信息误差越来越大，导致导航精度越来越低。

为此，国内外学者在此类问题上提出了3类解决办法：提高自身微惯性器件精度或增加其他导航传感器，但这会极大的提升硬件成本[3-4]。采用伪距与伪距率的组合方式，即便只接受1颗卫星信号时也采用紧组合，但此种方法过于依赖卫星信号的质量，无法保证精度的稳定性，况且此种方式增加了系统的复杂性[5-6]。近年来，人工智能算法逐步应用于辅助导航的解算，在GPS接收机失锁时，神经网络(NN)的修正与预测常被用于校正SINS的误差。文献[7-8]采用BP神经网络算法辅助组合导航，但BP网络容易陷入局部最小值，在部分网络训练不理想的情况下还会出现过拟合。BP算法在学习过程中收敛速度慢，泛化能力不优于RBF网络，在简单问题上学习时间过于冗长且在学习率上极不稳定[9]。文献[10]采用GRU循环神经网络辅助组合导航，但GRU循环神经网络训练次数过多，无法参考较长时间间隔的信息。在GRU中较远时间步的梯度消失导致其在训练过程中不能完全解决梯度消失问题。

本文提出了一种基于RBF网络的辅助导航算法，将SINS系统和组合导航系统输出的信息分别作为RBF网络的输入和输出，对其进行在线训练，在失锁时利用训练好的RBF网络补偿载体自身的速度和位置信息，并通过跑车实验验证其有效性。

1 组合导航系统模型

(1)

因SIN内部惯导测量组件相关时间很长，所以其相关漂移项可看作近似游走，其中一步转移矩阵F可简化为：

(2)

W(t)为6维的白噪声表示如下：

W(t)=[ωb,ωg,ωa]

(3)

噪声矩阵G(t)如下：

(4)

观测方程为：

(5)

其中观测量为SINS解算出来的与GPS接收机所得的速度、位置之差，Vk为高斯观测白噪声，Hk矩阵如下：

(6)

2 GPS失锁时的导航方案设计

2.1 RBF神经网络

神经网络是一种能大规模处理数据且进行并行分布的处理器，能够对非线性、随机性强的复杂问题建立模型[11]，前馈型神经网络常用来做惯性传感器输出信息的预测，常用的前馈型网络主要有RBF[12]和BP[13]网络，RBF网络能够以任意精度逼近任意连续非线性函数[14]，且训练时间短、次数少，所以本文采用RBF网络。

RBF网络包含1个输入层、1个隐含层和1个输出层。其训练过程可以概括为2个步骤。在隐层中使用的RBF特征必须首先确定权重然后确定输出神经元。在隐含层中，改变权重和偏差以最小化预测位置和速度的误差。在输出层，预测信息通过隐含层到节点的输出层，其中计算的值为隐神经元的线性和，RBF的网络结构如图1所示。

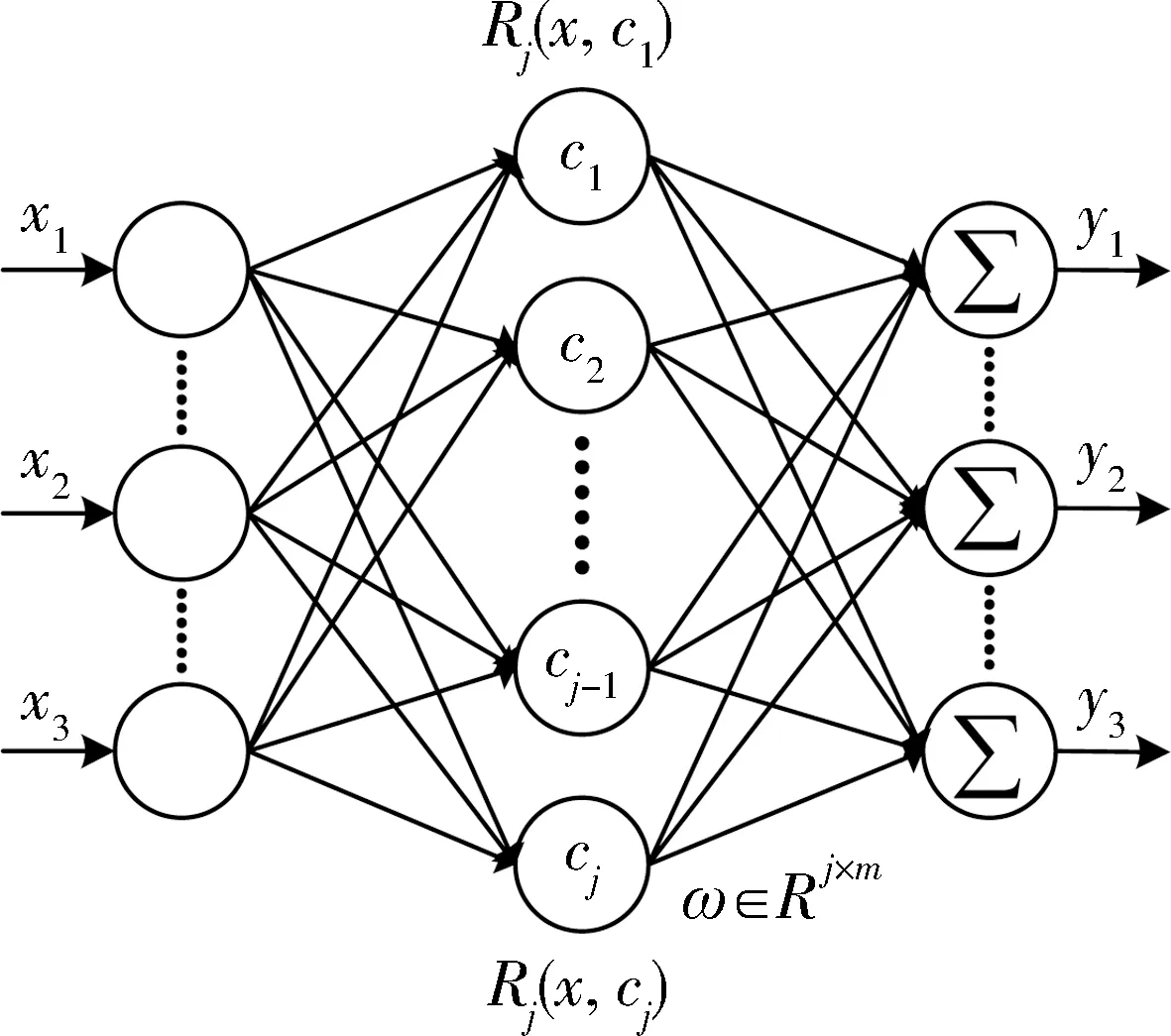
图1 RBF神经网络结构

在网络结构中，高斯函数作为RBF中的激活函数计算：

(7)

(8)

y是RBF神经网络的输出，wj=(wi1,wi2,…,wim)T表示每个神经元i的权值，H=[H1,H2,…,Hm]T是基本函数的向量，并且ο是网络单元输出的数量。

本文所使用的RBF网络流程为首先设置中心cj和权重wi，确认网络的输入和输出样本，用高斯函数计算神经网络的激活函数，再将所需要预测的样本输入训练好的网络，最后计算预测结果。

2.2 数据集简介

训练数据为惯导系统在400s内通过50Hz的采样率采集到的20000组历史数据，测试参数如下：SINS系统的东向和北向速度vESINS、vNSINS、东向和北向位置pESINS、pNSINS。理想期望数据为参考基准系统在400s内通过50Hz的采样率采集到的20000组历史数据，测试参数如下：vESINS/GPS、vNSINS/GPS、pESINS/GPS、pNSINS/GPS。其中训练数据与期望数据均在每一时刻一一对应。RBF网络在物理层面的意义在于参考基准观测值的位移和速度增量与前一时刻系统速度、姿态、INS系统在该时间间隔内的加速度和角速度增量存在某种非线性关系，基于RBF网络建立这种非线性模型的映射关系。

2.3 RBF网络辅助组合导航算法设计

RBF网络辅助组合导航具体流程为：本文的RBF网络选用输入输出聚类学习法来确定函数中心，此方法使得选取中心位于输入空间的重要位置，能提高网络拟合效果，基于最小二乘法求解网络权值。在GPS信号良好时，RBF神经网络的期望输出为通过卡尔曼滤波修正后的SINS/GPS组合导航系统提供的位置速度。即经滤波后的速度vsins/GPS、位置psins/GPS信息作为RBF神经网络的期望输出值，网络的输入值为SINS提供的速度位置姿态信息，然后进行网络训练，从而提高单纯捷联惯导系统解算出来的导航信息的精度。

当GPS在具体应用环境中无法搜索到信号或被系统提示异常时，即GPS信号失锁时，用训练好的RBF神经网络对SINS系统的速度vsins、位置psins信号进行处理并实时提供经过训练好的RBF神经网络解算出的速度位置信息。具体流程如图2所示，其中包含GPS良好时对网络的训练过程和信号失锁时对位置速度等信息预测以及修正过程。

图2 RBF网络辅助流程图

2.4 RBF网络训练过程

RBF网络训练过程如图3所示，x为RBF网络接收的SINS系统速度位置信息，N(t)为经滤波后的位置速度信息作为期望输出值，RBF网络通过在隐含层调整权值系数wi，使实际输出L(t)与期望输出N(t)之间的误差e降到最小从而结束训练。其中：

图3 RBF网络训练过程

(9)

式中，x=[vESINSvNSINSpESINSpNSINS]，

N(t)=[vESINS/GPSvNSINS/GPSpESINS/GPSpNSINS/GPS]，

L(t)=[vERBFvNRBFpERBFpNRBF]。

3 算法验证

3.1 实验设备设置

通过跑车实验验证了上述算法，训练样本均取真实数据，实验设备如图4所示，其中参考基准装置选择的是加拿大NovAtel公司的Span-lci系列高精度定位系统，实验装置采用的是CRM100陀螺仪和MS9010加速度计集成的IMU惯性测量装置，后文称其为SINS系统，将实验装置和参考基准设置成相同采样频率50Hz进行实验，跑车时间共500s，实验地点为中北大学6号楼前广场，前400s为卡尔曼滤波辅助组合导航过程，后100s人为关掉组合导航的GPS接收机，模拟GPS信号失锁，只接收SINS系统的速度位置信息,系统变为纯惯导模式，再通过训练好的RBF网络对捷联惯导系统(SINS)的位置速度信息进行修正。实验设备的主要参数如表1所示。

图4 实验设备

表1 实验设备主要参数

3.2 实验结果分析

通过实验分别分析了模拟GPS失锁后，即400s～500s时，3个不同系统解算出的速度和位置信息。3个系统分别为：纯惯导系统(SINS)、参考基准系统、通过RBF神经网络辅助的SINS系统(SINS+RBFNN)。本实验将Span-lci系列高精度定位系统定为参考基准。

图5为SINS与参考基准解算的东向速度对比，在470s后，SINS解算出的东向速度发散现象严重。图6为SINS+RBFNN与参考基准解算出的东向速度对比，可见，当GPS信号失锁时，本文设计的RBF神经网络模型可有效辅助SINS，使得东向速度发散现象减小。图7为SINS和SINS+RBFNN解算的东向速度分别与参考基准的误差对比。

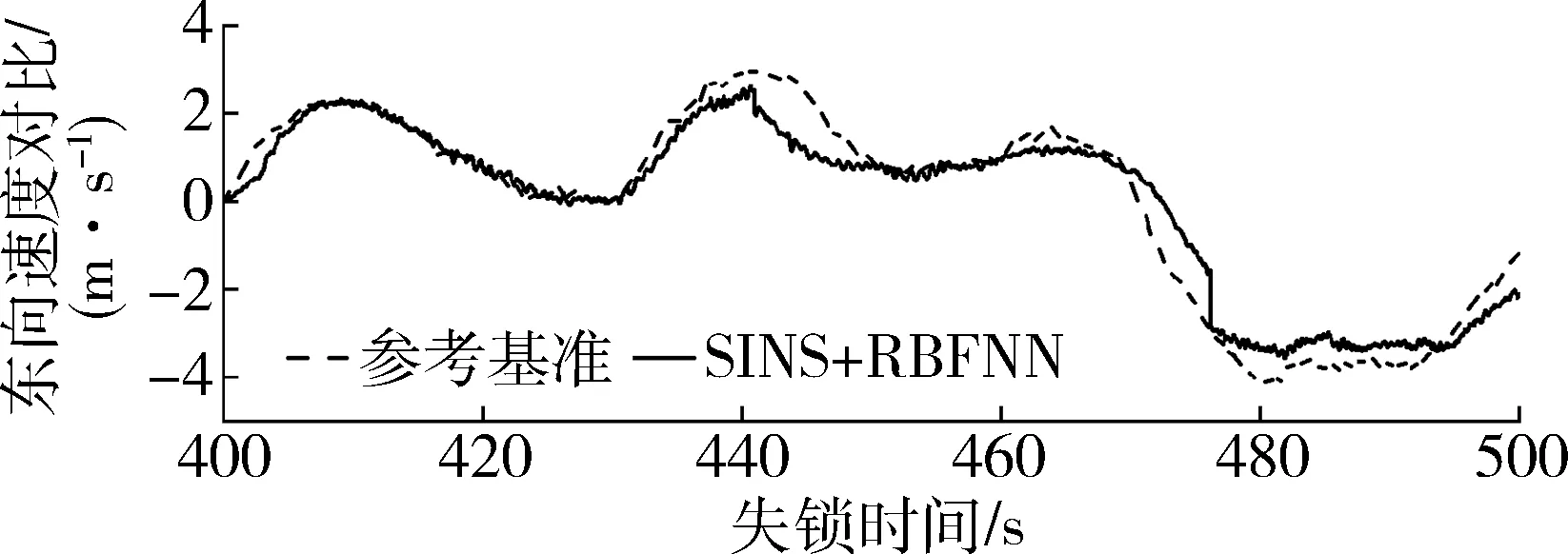
图6 神经网络辅助SINS后的东向速度

图7 有无神经网络辅助SINS东速误差对比

由图5～7分析可知，SINS解算出的东速平均误差为1.5m/s，在493s时误差值最大，达到4.1m/s。经SINS+RBFNN解算后的东速平均误差为0.36m/s，在440s～448s和469s～476s内平均误差最大，达到1.1m/s，在443s时误差值最大，达到1.4m/s。由此可知，通过SINS+RBFNN解算的东速误差相比于SINS解算出的平均误差降低了1.14m/s，在493s时，将SINS解算出的最大误差由4.1m/s降到了0.46m/s。

图5 无神经网络辅助东向速度

实验对比了不同系统解算出的北向速度，如图8～10所示。通过分析可知，SINS解算的北速最大漂移量达到了3.8m/s，平均误差为1.27m/s。SINS+RBFNN解算的北速最大漂移量为0.9m/s，平均误差为0.32m/s，相较于SINS降低了0.95m/s。

图8 无神经网络辅助北向速度

由于RBF网络能在克服局部最小值的问题下达到最佳逼近性，且网络的非线性拟合能力极强，在训练过程中，学习收敛速度快，网络逼近SINS系统误差发散模型准确，所以对其速度信息修正的更加精确。

SINS与SINS+RBFNN解算出的东向位置如图11～12所示。SINS和SINS+RBFNN解算的东向位置分别与参考基准的误差对比如图13所示。分析可知，在失锁的100s内，SINS解算出的东向位置平均误差为40.97m/s。SINS+RBFNN解算出的平均误差为3.14m/s，相较于SINS降低了37.83m。在484s时，SINS解算出的东向位置误差最大，达到了109.97m，同一时刻下，SINS+RBFNN的误差为3.56m，降低了106.41m。

图9 神经网络辅助SINS后的北向速度

图10 有无神经网络辅助SINS北速误差对比

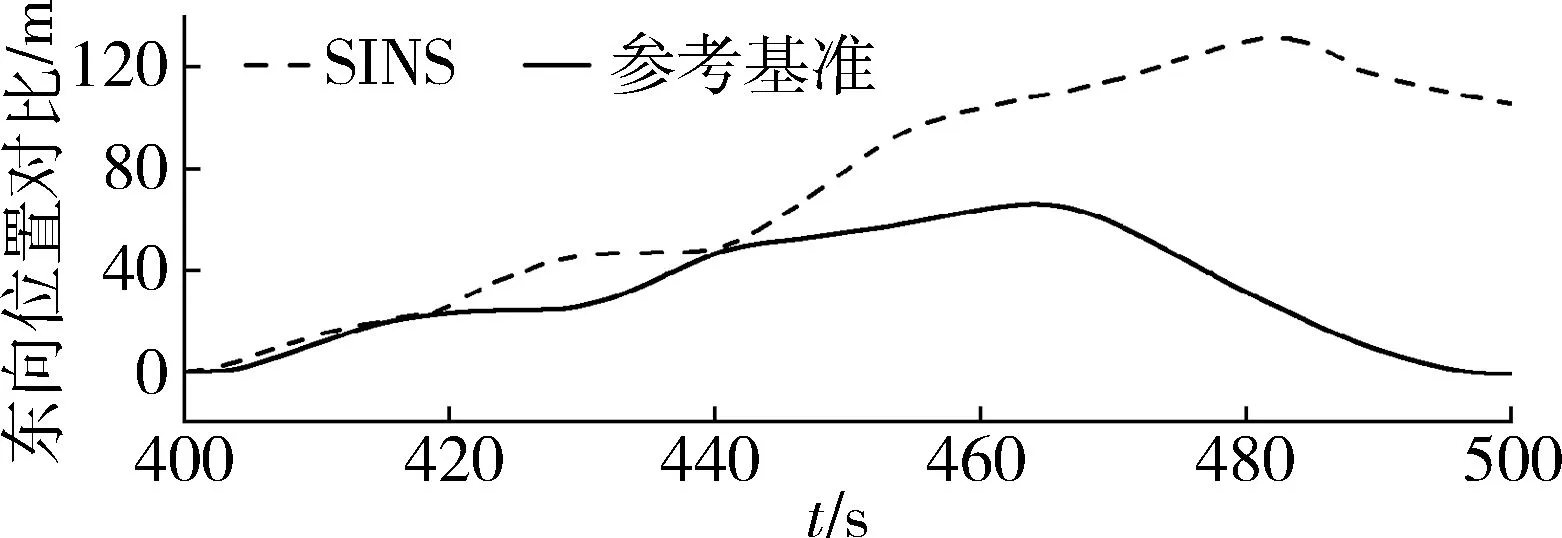
图11 无神经网络辅助的东向位置

图12 神经网络辅助SINS后的东向位置

图13 有无神经网络辅助SINS东向位置误差对比

由图14～16分析可知，SINS解算出的北向位置最大误差186.02m，平均误差80.11m。SINS+RBFNN解算出的北向最大误差19.36m，平均误差2.61m。

图14 无神经网络辅助的北向位置

上述位置信息对比分析表明，通过本实验设计的RBF神经网络模型所辅助的SINS系统，可有效改善GPS失锁引起的位置发散现象。

图15 神经网络辅助SINS后的东向位置

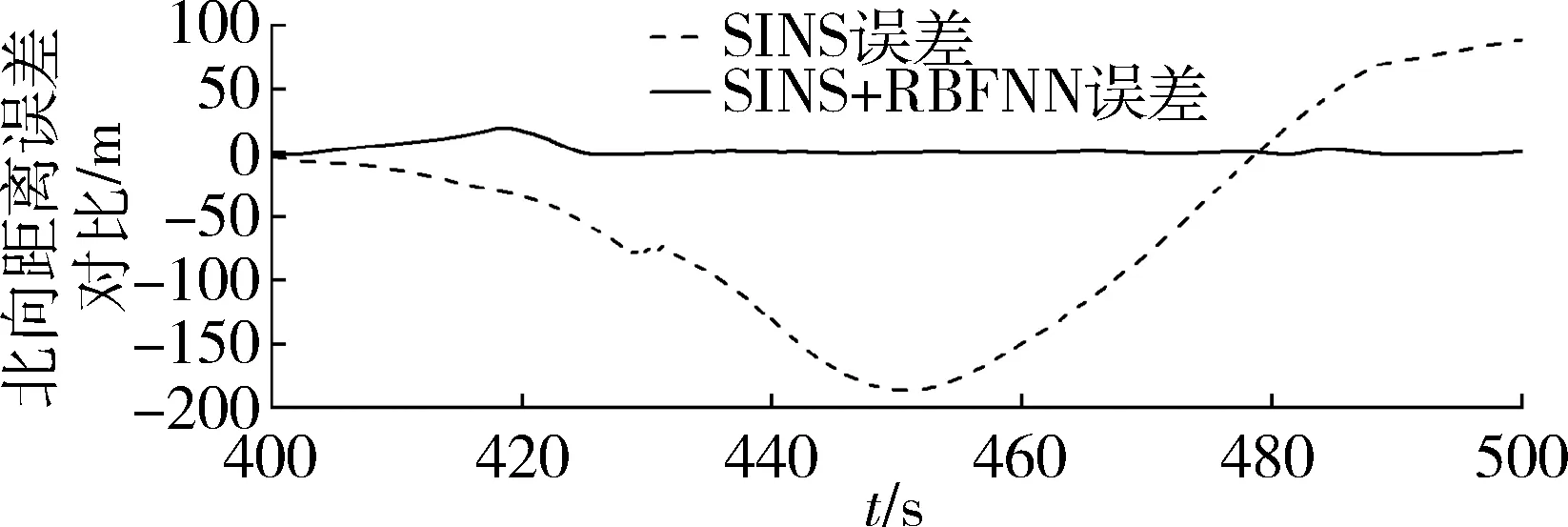
图16 有无神经网络辅助SINS北向位置误差对比

SINS和SINS+RBFNN与参考基准解算的东北方向二维位置对比如图17～18所示。通过二维平面位置可看出SINS在GPS失锁后的100s内，位置信息的发散现象严重，并没有构成完整的实际跑车轨迹回路，终点位置与实际终点位置偏离巨大。SINS+RBFNN解算的轨迹信息构成了实际路径的闭合回路，虽在过程中有些许偏离实际轨迹，但误差远小于SINS解算的位置信息。

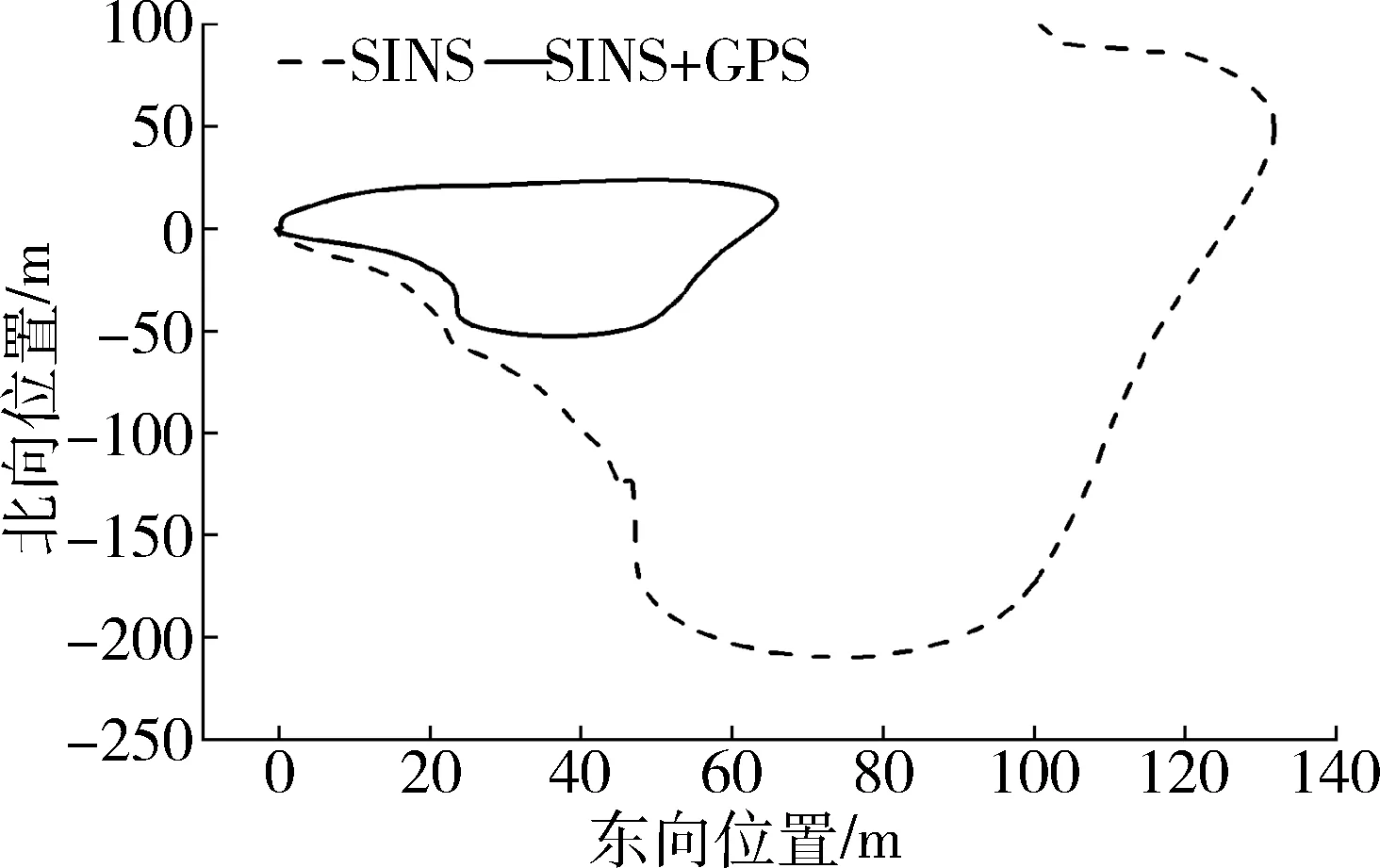
图17 无神经网络辅助的二维位置

图18 神经网络辅助SINS后的二维位置

4 结论

针对GPS信号失锁导致GPS/SINS无法工作的情况，设计了RBF神经网络辅助组合导航的算法，并通过跑车实验验证了该算法在导航中的精度。实验结果表明，速度平均误差在0.36m/s以内，位置平均误差在3.14m以内。分析可知，SINS+RBFNN解算的速度和位置误差远小于SINS解算的速度和位置误差。由于神经网络学习效果的时效性，致使训练效果只能在短时间内存在并有效，当GPS失锁超过一定时间后，RBF训练后的网络对组合导航预测的准确度与修正的精度会下降。但在实际情况中，100s的时间基本能够满足要求并在一定限度内有效提升导航精度。