卫星星载转台扫描路径规划与星体抗扰姿态控制*

张小伟 刘 笑 尹俊雄 祝 贺 袁彦红, 徐家国, 李 爽 周静静

1.南京航空航天大学航天学院，南京 211106 2.上海航天控制技术研究所，上海 201109 3.上海市空间智能控制技术重点实验室，上海 201109

0 引言

卫星在轨任务日益复杂多样，由传统的对地遥感，扩展到空间目标监视、星间/星地通信、导航定位等领域，即使对地遥感任务，也由传统的点目标或小区域目标成像等简单任务拓展到大范围宽幅成像、拼接成像等复杂任务。这些任务对载荷的扫描跟踪能力和灵活机动能力都提出了越来越高的要求。为满足上述要求，需将光学相机或微波天线等载荷部件固连于星载转台，利用转台驱动灵活、快速、精确的特性完成对目标的扫描、捕获、跟踪等相机视场或天线波束的指向任务。当转台的转动惯量相对星体惯量较大时，转台的运动，尤其是扫描运动与星体姿态运动耦合明显，对星体产生较大扰动，严重时甚至造成姿态失稳[1]。不考虑转台扰动的常规卫星姿态控制器通常受限于控制系统带宽，无法对姿态偏差快速响应，难以实现快速高精度的姿态稳定。实际工程中，此问题可以从两方面着手解决：1)在不牺牲任务效能的前提下优化转台的运动路径，减小对星体的扰动；2)同步补偿扰动力矩，尽最大可能抵消扰动对星体姿态的影响。

合理的运动路径规划可使运动状态平滑缓变，减小控制难度的同时，控制精度也更易实现，文献[2]利用三角函数规划姿态角加速度，实现了星体姿态的快速平稳机动。文献[3]针对空间机械臂的捕获任务，利用双臂产生的角动量平衡原理，用非操作机械臂的运动来平衡操作臂带来的干扰。文献[4]对地面精密转台设计了S曲线运动轨迹，并在双闭环反馈控制基础上增加了扰动补偿与前馈补偿，有效提升了转台的动态精度与稳定度。文献[5]规划了加速度约束下的星体姿态轨迹，并基于前馈补偿与跟踪误差反馈相结合的方式进行姿态控制。文献[6]在已知转动部件运动规律的情况下，设计了前馈-反馈的复合控制算法，消除了运动部件对星体的负面影响，实现了较高精度的姿态控制。文献[7]针对旋转载荷周期性扰动设计了基于参数辨识的自适应控制算法，有效提高了姿态稳定度。此外，神经网络估计扰动力矩补偿控制[8]、鲁棒模糊控制[9]、自适应自抗扰控制[10]和基于扰动观测器的前馈补偿控制[11]等方法也被用于补偿控制器设计，但这些方法运算量大，工程应用难度较大。

本文以大惯量二维转台对地面特定区域快速扫描为任务背景，利用阿基米德螺旋线[12]进行载荷波束指向星下点扫描路径规划，再结合卫星轨道信息解算转台的二维转角指令。利用转台的机械参数和质量特性数据进行转台精确运动学建模，得到星体+转台耦合的姿态动力学方程。利用运动学模型和转台转角，计算转台对星体的扰动力矩并对其进行实时补偿，再叠加改进后的PD反馈控制，形成前馈+反馈复合控制结构，通过考虑了一定工程因素的数字仿真验证了控制器的有效性。

1 扫描路径规划

在卫星过顶时，载荷波束(泛指相机视场和天线波束)需要在特定时间内完成对地面指定区域的扫描覆盖，在扫描时长受限的情况下，传统的S形扫描在扫描轨迹换向处角加速度变化剧烈(甚至是阶跃形的突变)，对星体干扰很大，而且对转台的驱动和控制能力要求也较高。优化设计平滑缓变的扫描轨迹，可以减小转台对星体的扰动，降低补偿难度。

利用地理经度λ和地理纬度φ′描述载荷波束指向的地面星下点位置，采用等角速率的阿基米德螺旋线来规划载荷指向在地面的轨迹变化

(1)

图1 阿基米德螺旋线轨迹

(2)

根据文献[13]方法将地理经纬度坐标(λ,φ′)转化为地心经纬度坐标(λ,φ)，进而得到地心惯性系下扫描点赤经α、赤纬δ

(3)

式中：G0为t0时刻格林威治的恒星时角；ωe为地球转速。

则地心惯性系下的扫描点位置向量为

(4)

(5)

式中：Roi和Rbo分别为惯性系到轨道系和轨道系到星体系的姿态转换矩阵；Rx(α)和Ry(β)分别为绕X轴旋转α角和绕Y轴旋转β角对应的姿态转换矩阵。

2 精确动力学建模

依转台结构将转台分为仅绕外框转动的A部分，及安装载荷(光学镜头或微波天线)可绕内框旋转，并随外框一起转动的B部分，转台与星体结构坐标关系如图2所示。

图2 转台与星体相对安装关系示意图

图中坐标系定义如下：

a)卫星本体坐标系OXbYbZb：O为整星质心，三轴与卫星惯量主轴平行，简称星体系；

b)转台安装坐标系O1XytYytZyt：O1为A部分转轴与其安装面交点，三轴与星体系重合，简称转台安装系；

c)A部分固连坐标系O1Xyt-xYyt-xZyt-x，原点同O1XytYytZyt，三轴随A部分绕外框轴转动，转角为α，正负按右手坐标系定义，α=0时与转台安装系重合，简称A固连系；

d)B部分固连坐标系O2Xyt-yYyt-yZyt-y，O2为B部分的转轴与其在A部分上的安装面交点，三轴随B部分绕转轴转动，转角为β，正负按右手坐标系定义，在α=β=0时与转台安装坐标系重合，简称B固连系。

图2中c1和c2分别为A和B部分质心，dm为质量微元，ωα和ωβ分别为A部分绕外框、B部分绕内框的转动角速度，其转角分别为α和β，roo1等其他位置矢量的符号含义见图中示意。

2.1 A部分运动学模型

A部分绕卫星质心的相对角动量

(6)

式中：r1=roo1+ρ1为O到A部分质量微元dm的矢量，v1=droo1/dt+dρ1/dt=ωα×ρ1(droo1/dt=0)为dm相对于O的线速度。

(7)

(8)

2.2 B部分运动学模型

令m2为B部分的质量，B部分绕卫星质心的相对角动量为

((ωα+ωβ)×ρ2)dm+

(9)

式中：r2=roo1+ro1o2+ρ2为O点到B部分质量微元dm的矢量；v2=droo1/dt+dro1o2/dt+dρ2/dt=ωα×ro1o2+(ωα+ωβ)×ρ2(droo1/dt=0)为dm相对于O点的线速度。

(10)

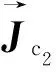
转台总角动量为：

(11)

2.3 整星姿态动力学方程

星体坐标系下表述的含二维转台的整星动力学方程为

(12)

3 抗扰姿态控制器设计

常规的纯反馈控制律由于带宽受限，难以对转台扰动造成的姿态偏差作出快速响应，因而需要对2.3节计算得到的干扰力矩进行实时补偿。实际工程中，软件解算、数据传输等环节产生的延时，转台和飞轮的响应特性的差异，星体质心变化等因素会对补偿产生不利影响，导致补偿存在残差，该残差力矩会使星体姿态误差变大，且由于其量级比环境干扰力矩大，对星体姿态误差的放大作用比常规无转台干扰卫星快得多。要快速消除残差对姿态的干扰，需对控制器中的PD反馈部分改进，调高控制带宽，增大开环增益，以提高响应快速性和稳态精度，同时还要保留足够的稳定裕度。

综合上述措施，形成PD反馈控制与干扰前馈补偿的复合抗扰姿态控制器，控制系统结构如图3所示。

图3 控制系统框图

转台扫描期间工作流程：利用卫星实时位置与姿态信息，按照预设的扫描轨迹，根据式(4)和(5)，解算转台的转角指令，并发送给转台伺服电机；根据转台转角指令差分求其转速，根据式(8)、(10) 和(11)计算出转台干扰角动量，再差分求得干扰力矩并作为前馈补偿量；反馈控制部分根据姿态角与角速度信息，计算反馈控制力矩，与前馈补偿力矩的和作为飞轮的指令力矩，并与转台控制指令同时发出；为进一步改善控制效果，对姿态动力学方程中的非线性耦合项也进行补偿。形成控制律如式(13)。

Tc(k)=Kp(θr(k)-θm(k))+

(13)

4 仿真校验

转台的动力学模型参数如表1所示。

表1 转台参数

根据规划的螺旋扫描轨迹式(1)和(2)，计算所得的转台转角与转速如图4所示，再根据式(8)和(10)计算的角动量如图5所示，可见两者均连续平滑缓变。

图4 转台的转角与转速

图5 转台的三轴角动量

卫星运行于近地圆轨道，仿真中还考虑了敏感器测量噪声、补偿延时等工程误差因素，相关参数详见表2。

表2 星体与控制系统相关参数

注意：为符合常规表述，表中位置矢量或惯量张量为在相应固连坐标系下的表示，根据式(8)和式(10)计算时需将其转换到星体系下。

姿态仿真结果如图6和7所示，转台扫描过程中，在复合控制器作用下，星体姿态指向精度优于0.002°，姿态指向稳定度优于0.002(°)/s，实现了转台快速扫描期间星体姿态的高精高稳指向。

图6 姿态角

图7 姿态角速度

5 结论

针对星载大惯量转台快速扫描期间维持星体高精度姿态控制的任务需求，本文基于阿基米德螺旋线进行星下点扫描路径规划，在确保对目标区域的覆盖特性的同时减少了对星体的扰动。基于建立的二维转台精确运动学模型，实时计算和补偿转台干扰，同时通过改进的高带宽反馈控制器抑制补偿残差产生的姿态误差，并通过仿真验证了控制器的有效性。