圆锥曲线焦半径公式的解题应用

杨苍洲

(福建省泉州第五中学 362000)

1 圆锥曲线的焦半径公式

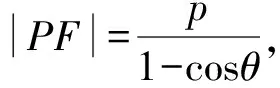
2 焦半径公式在抛物线中的应用

题1 己知抛物线y2=8x，O为坐标原点，过抛物线焦点F的直线交抛物线于A,B两点，|AB|=10，则△OAB的面积为( ).

解析设直线AB的倾斜角为θ，则

所以|AB|=|AF|+|BF|

又因为|AB|=10，

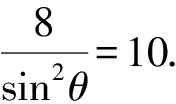
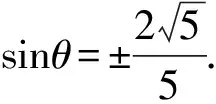
故选A.

题2 设抛物线y2=2px(p>0)的焦点为F(1,0)，准线为l，过焦点F的直线交抛物线于A,B两点，分别过点A,B作l的垂线，垂足为点C,D，若|AF|=4|BF|，则△CDF的面积为( ).

解析抛物线y2=2px(p>0)的焦点为F(1,0)，则p=2.

设直线AB的倾斜角为θ，则

又因为|AF|=4|BF|，

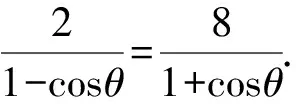
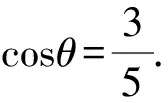
因为|AB|=|AF|+|BF|

所以|CD|=|AB|·sinθ

=5.

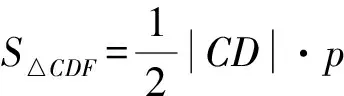
=5.

故选C.

3 焦半径公式在椭圆中的应用

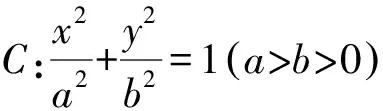
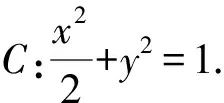
设直线AB的倾斜角为θ，

则|AB|=|AF2|+|BF2|

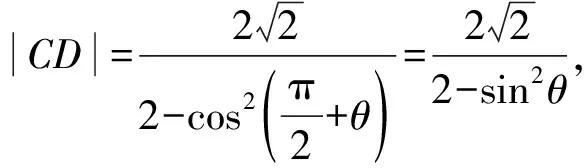
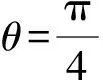
4 焦半径公式在双曲线中的应用

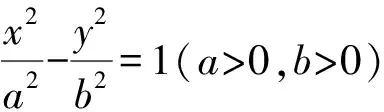
解析设直线AB的倾斜角为θ，则

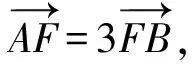
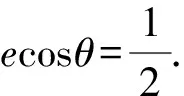
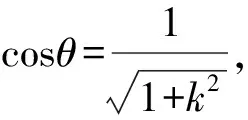
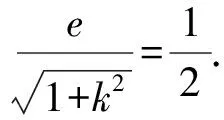
所以k2+1=4e2.

题5 已知双曲线H的两条渐近线互相垂直，过H右焦点F且斜率为3的直线与H交于A,B两点，与H的渐近线交于C,D两点.若|AB|=5，则|CD|=( ).

解析设直线AB的倾斜角为θ，

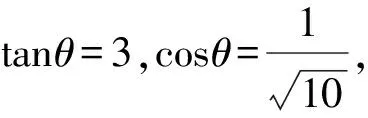
|AB|=|AF|+|BF|

又因为|AB|=5，

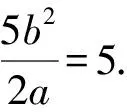
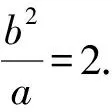
又a=b，

所以a=b=2.

两条渐近线的方程分别为y=x,y=-x.

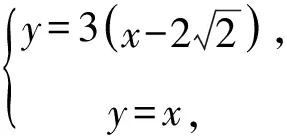
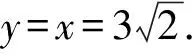
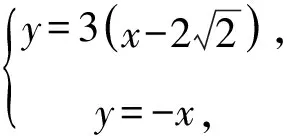
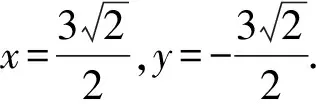
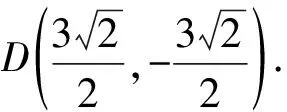
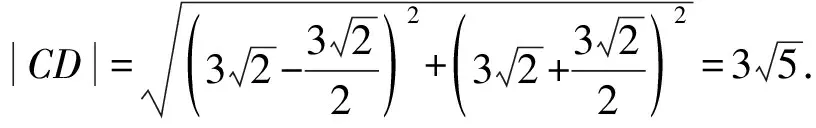
故选C.