高比例新能源电力系统频率稳定性的惯量需求分析

张桂红，刘 飞，王世斌，李积泰

（国网青海省电力公司经济技术研究院，西宁 810008）

随着以风电和光伏等为代表的换流器并网新能源规模化开发和利用，新能源的渗透率逐渐增高[1]。一方面是响应了国家对“双碳”目标的要求[2]，有利于解决环境污染问题；另一方面，传统同步发电机逐渐被替代，降低了系统惯量[3]，将会引发电力系统的频率稳定性出现问题。

中国提出在2030年实现碳达峰，2060年实现碳中和，并于2030年实现光伏装机和风电装机总容量达到1 200 GW的目标[4]。因此，对于换流器高占比电力系统急需发展新的频率控制技术，以应对高比例新能源接入后系统惯量不足的问题。传统电力系统中，系统的频率稳定性往往依赖于同步发电机的调节能力，当系统突然遭受大的功率波动时，其储存的转子动能可减缓系统频率跌落的速度[5]。相较于同步发电机，新能源通过换流器与电网相连，其功率与频率解耦，且新能源的最大功率追踪控制技术使得其提供的惯量水平不足[6]。为了衡量电力系统的频率稳定性[7]，现有研究主要关注频率变化率RoCoF（rate of change of frequency）和频率最低点FN（frequency nadir）。例如，2016年澳洲的“9.28大停电”[8]事故，持续时间近10 h。澳洲风电装机和光伏装机容量总占比将近50%，事故导致南澳损失功率达956 MW，电网频率降低至49.5 Hz以下并迅速跌落，最终致使电网频率崩溃。2019年英国“8.9大停电”[9]事件，持续时长为1.5 h，RoCoF超过新能源脱网动作阈值，进而使得频率跌落触发低频减载装置动作，出现大面积停电事故。这两次事故[10-11]分别造成南澳电网和英国电网损失1.826 GW和1.878 GW负荷，事故造成的影响比较大。经众多学者分析，这两起事故均是由于电网的惯量支撑能力以及同步机组调频能力不足导致的。因此，有必要开展电力系统惯量水平的评估与分析，并充分发挥源网荷侧非同步机组调频资源的频率调节能力。

为了更好的量化分析系统的惯量水平，文献[12]通过惯量安全域来帮助调度运行人员快速甄别惯量水平的安全程度，提供低惯量预警机制，快速评估系统的频率稳定性，但是其构建的惯量安全域是时变的，会随着系统的运行工况而发生变化，且需要构造N-2故障集。文献[13]通过给惯量定价，使得参与惯量响应的风机系统以及储能系统得到应有的补偿，并基于机会约束综合考虑新能源的不确定性，提出电能量、备用以及惯量响应联合出清模型，但在考虑最小惯量估计时仅考虑了频率变化率约束，未考虑频率最低点约束，结果可能过于乐观。

本文综合考虑频率变化率约束和频率最低点约束，给出系统所需最低惯量需求，进而构建惯量可行区间。在此基础上，通过虚拟惯量技术，提高系统的惯量支撑能力，从而提高系统的频率稳定性。

1 系统惯量特性与需求

1.1 电力系统惯量特性

电力系统惯量是指同步发电机主导的电力系统中阻碍旋转动能变化速度的能力。当发电功率与负荷功率出现不平衡时，电力系统的频率响应存在4个不同时间尺度的过程：惯量响应过程、一次调频过程、二次调频过程以及三次调频过程，如图1所示。其中，惯量响应过程由同步惯量和虚拟惯量来支撑，一次调频过程可由再热器、原动机和调速器协调配合实现，本文中的频率响应过程主要考虑惯量响应过程和一次调频过程。

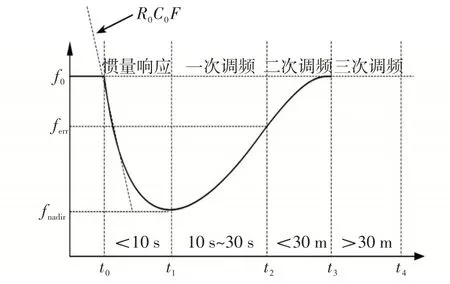
图1 频率响应特性Fig.1 Frequency response characteristics

图2 为不同渗透率水平下的惯量和频率控制技术发展路线示意图。随着新能源渗透率的不断提高，系统惯量水平逐渐降低，为进一步提高系统的频率稳定性，需要采用新能源机组的虚拟同步技术。就惯量水平而言，由于风机转子存储有旋转动能，可用于主动提供一定的惯性支撑，而光伏只能配合储能系统为系统提供惯性支撑。

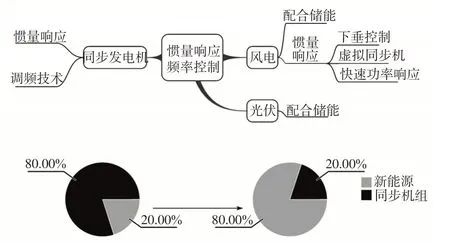
图2 惯量和频率控制技术Fig.2 Inertia and frequency control techniques

系统的频率响应过程可用如下等值转子运动方程[14]描述为

式中：Hsys为等值惯性常数；fN和Δf(t)分别为系统额定频率和频率波动值；D为负荷频率响应系数；PG(t)为系统一次频率响应功率；Pmec(t)为系统的机械功率；Pele(t)为系统的电磁功率。

对于以同步机为主导的电力系统，当事故发生时，由于死区的存在，调速器不能及时将功率变化注入系统，而新能源的快速调频一般也设有延时，需要指出的是，惯性只是利用转子中存储的旋转动能来缓冲不平衡功率，但并未解决不平衡问题。但是惯性可阻碍频率的变化，因此在调速器或新能源快速调频动作前，仅有惯量在参与支撑系统有功功率平衡。综上所述，惯量在频率稳定分析中占有重要地位，可用于缓冲不平衡功率从而减缓频率变化速度，为一次调频响应赢得更多反应时间。

1.2 电力系统惯性需求

1.2.1 考虑频率变化率约束的最小惯量

RoCoF是衡量扰动下系统频率稳定性的关键指标。在扰动初期，由于发电机调速器等还未动作，系统可参与的频率调节手段最少，故此时的Ro⁃CoF应最大，可将其作为系统频率约束指标。

为避免同步机产生滑极现象，损坏同步机内部结构，文献[15]建议RoCoF不得超过2 Hz/s；文献[11]也提出，为防止扰动后分布式电源脱网，RoCoF不应超过分布式电源设备级孤岛保护整定值0.125 Hz/s。在实际应用时，可针对电网实际需求，灵活选取合适的频率变化率作为系统最大频率变化速度约束RoCoFmax。

若以扰动后不触发系统安稳装置动作为基准，则系统频率变化率仅取决于系统的惯量水平与功率缺额。由转子运动方程可得最小惯量常数为

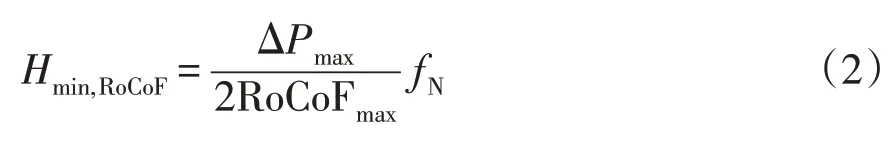
式中：ΔPmax为最大功率扰动；RoCoFmax为系统最大频率变化速度约束。

电力系统的惯性支撑可减缓系统频率变化速度，通常用系统惯量来描述电力系统的惯性，采用能量形式为

式中：Esys为系统总惯量水平；ESG为同步机惯量，是由同步机提供的实时自发且无延时的惯量支撑；EVSG为虚拟同步机惯量，是通过虚拟同步机技术实现的惯量统称。

定义惯性时间常数TJ为施加额定转矩将发电机由静止拖动到额定转速所需要的时间，其系统惯性常数Hsys的关系为

基于惯性时间常数，可将系统最小惯性需求表示为

式中，Ssys为系统容量。

1.2.2 考虑频率最低点约束的最小惯量

当频率变化触发一次调频动作时，调速器将增加机械功率输入以减少系统功率偏差，从而进一步抑制频率的跌落。一般地，近似认为当机械功率输入和电磁功率输出相等时，系统频率达到最低值fnadir。为避免触发低频减载安稳装置动作，频率最低点也是衡量系统频率稳定的关键指标，需要满足

式中，fmin为频率安稳装置动作值下限。可采用文献[12]中的线性模型近似求解系统的频率最低点，即

（1）一次调频死区环节为

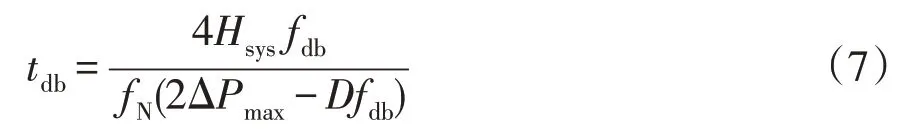
式中：fdb和tdb为一次调频控制死区和动作时间；D为频率响应过程中的阻尼效应。

（2）一次调频响应环节为

式中：tnadir为频率到达最低点时的时间；Rsys为系统一次调频速率。

经整理，可得频率最低点的计算公式为

将式（9）代入频率约束（6）后可得最小惯性为

综合考虑频率变化率约束和频率最低点约束，可求得系统最小惯量常数为

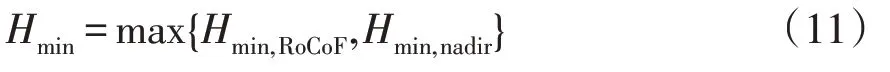
1.3 虚拟惯量分析

1.3.1 风电机组

双馈风机是目前并网运行的主要风机类型，通过调整其控制策略，可使风电机组主动响应系统的频率变化，实现与同步机类似的惯量响应过程。

风机的转子运动方程为

式中：ΔPω为风机频率响应功率；Mω为风机的虚拟惯量。

基于虚拟同步机技术，综合考虑惯量响应与一次调频过程[16]，可使风电机组主动参与一次调频，则式（12）变为

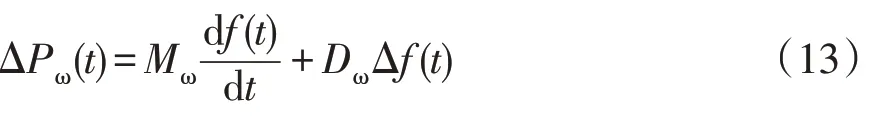
式中：Dω为风机下垂系数，模拟一次调频能力。

1.3.2 光伏机组

光伏系统内部无旋转动能，故不能像风机一样提供虚拟惯量，但仍然可以采用虚拟同步机技术模拟惯量响应和一次调频过程，即

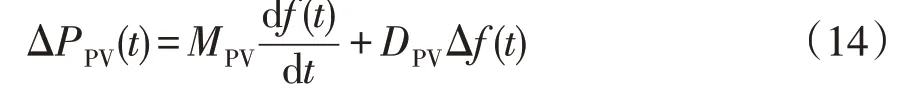
式中：DPV为光伏下垂系数，模拟一次调频能力；MPV为光伏的虚拟惯量。

1.3.3 储能系统

储能系统具备快速响应特性，可以很好地满足惯量响应过程和一次调频过程的快速动作需求。储能的运行约束为

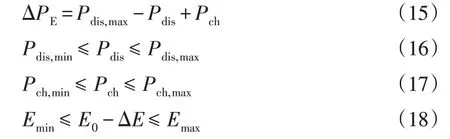
式中：Pdis,max、Pdis,min分别为储能系统放电功率上、下限；Pch,max、Pch,min分别为储能系统充电功率上、下限；Pch、Pdis分别为储能系统充放电功率；E0、Emin和Emax分别为储能系统电量初始值、最小值和最大值。

如果将储能系统与新能源作为一个整体并网运行，则除了新能源本身的惯量响应外，储能系统也能提供虚拟惯量支撑，且更为可控，从而使得新能源-储能联合系统具有和同步机相同的频率响应效果。

基于动态频率特性，储能系统可参与等效虚拟惯量和调频动作。储能系统参与惯量响应与一次调频时，其转子运动方程为

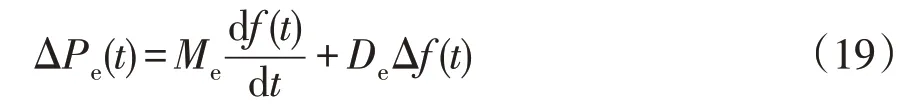
式中：De为储能的下垂系数，模拟一次调频能力；Me为储能的虚拟惯量。

2 新能源并网系统频率稳定分析

2.1 基于惯量水平的频率稳定分析

由式（5）可知，当功率缺额一定时，系统的惯量水平与频率变化率成反比。系统惯量水平与频率变化率的关系如图3所示，当系统处于临界惯量水平时，频率变化率将达到安稳装置动作阈值，此时调度人员应考虑储备一定的惯量备用以应对突发状况；当系统惯量不足时，频率变化率过快还可能导致新能源机组脱网，从而给系统带来新的干扰，进一步恶化频率稳定性。

图3 惯量水平与频率变化率关系Fig.3 Relationship between inertia level and RoCoF

除频率变化率外，频率最低点同样与系统惯量水平密切相关。依据1.2.2节分析可知，频率最低点是一次调频动作后系统频率变化达到的最小值，但如果系统惯量水平不足，则可能先期触发低频减载动作，造成大量负荷损失。

综上所述，在评估系统惯量水平时，应计及最大频率变化率约束和频率最低点约束，进行系统最小惯量水平的分析计算。

2.2 惯量可行区间

如图4所示，惯量可行区间是指在由同步机惯量和虚拟惯量构成参数空间内，满足频率稳定的安全区间，可行区间边界即最小惯量需求。通过构建惯量可行区间，可将不同来源的惯量提供方进行耦合分析，帮助调度人员直观判断当前系统运行点是否处于频率稳定状态。

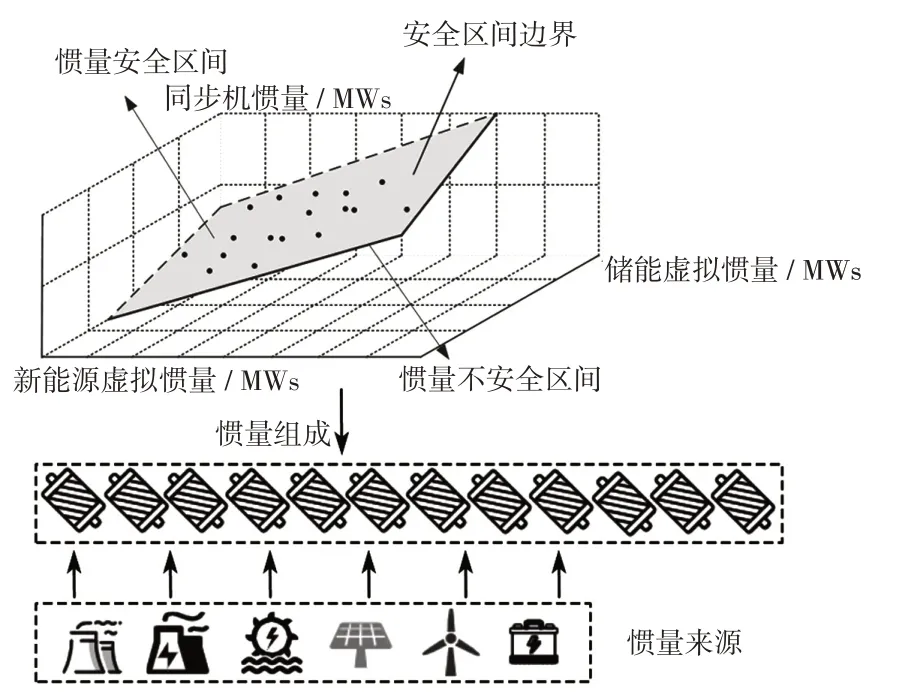
图4 惯量可行区间示意Fig.4 Schematic of feasible interval of inertia

依据1.2节分析可知，为保证频率稳定，系统需满足最小惯量需求，即系统内同步机组惯量、新能源机组虚拟惯量以及储能系统虚拟惯量总和应不小于最小惯量需求，即

式中：Msys为同步发电机组惯量；Mmin为最小惯量需求，惯量单位均为MWs。

3 算例分析

以某地区实际电网等值系统进行仿真验证，系统网络拓扑结构如图5所示，其中新能源机组总出力5 370 MW，同步发电机组总出力1 886 MW，渗透率为74%，各节点发电、负荷组成如表1所示，单位为MW。同步发电机组惯性常数设为4 s，一次调频系统的调差系数为0.05。算例仿真平台为PSCAD/EMTDC，计算配置为Intel（R）Core（TM）i7-8650U CPU@1.90 GHz、内存16 GB。

图5 示例系统网络拓扑Fig.5 System network topology of example

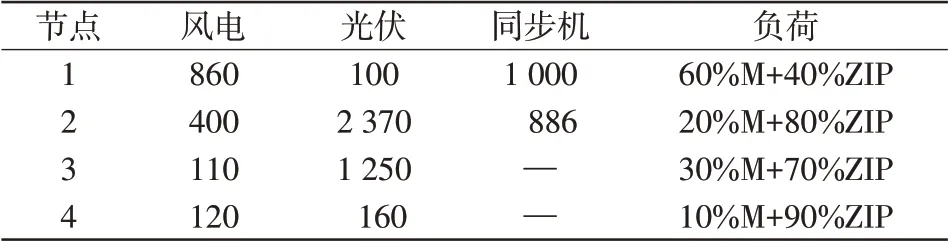
表1 负荷情况Tab.1 Load components

3.1 惯量需求分析

考虑新能源波动机组出力减少的情况，假设新能源出力损失10%（537 MW），在不考虑一次调频和负荷阻尼的情况下，依据公式（5）计算可知，若系统允许的最大RoCoF为0.25 Hz/s，则系统最小惯量需求为107 400 MWs。还可求得系统中同步发电机组能提供的惯量支撑为2×1 886 MW×4 s=15 088 MW·s，故还需虚拟惯量提供支撑92 312 MW·s。进一步考虑不同功率缺额和频率变化率，并重复上述计算过程，可得到的惯量灵敏度分析如图6所示。

由图6可知，最小惯量需求会随着系统功率缺额的增加而变大，随着最大频率变化率的增加而变小，且上述变化趋势在系统功率缺额较大和最大频率变化率较小时更为明显。

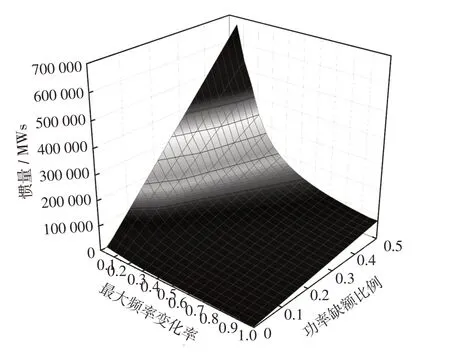
图6 惯量灵敏度分析Fig.6 Inertia sensitivity analysis

3.2 频率稳定分析

依据3.1节计算得到的系统最小惯量需求，利用虚拟同步技术评估当前运行方式下新能源和储能系统的惯量支撑水平，进而判断系统的频率稳定性。构建不同运行点，具体如表2所示，运行点1为3.1节计算的临界惯量水平，运行点2为无虚拟惯量支撑的惯量水平。不同惯量水平下系统频率响应的仿真曲线如图7所示，图7（a）中，运行点1的惯量水平严重不足，此时运行点位于可行区间外，频率最低点达到48.8 Hz，触发低频减载动作，容易造成频率失稳；图7（b）中，运行点2的惯量水平达到临界需求，此时运行点位于可行区间内，频率最低点达49.5 Hz，系统达到临界稳定。

表2 不同运行点Tab.2 Different operating points

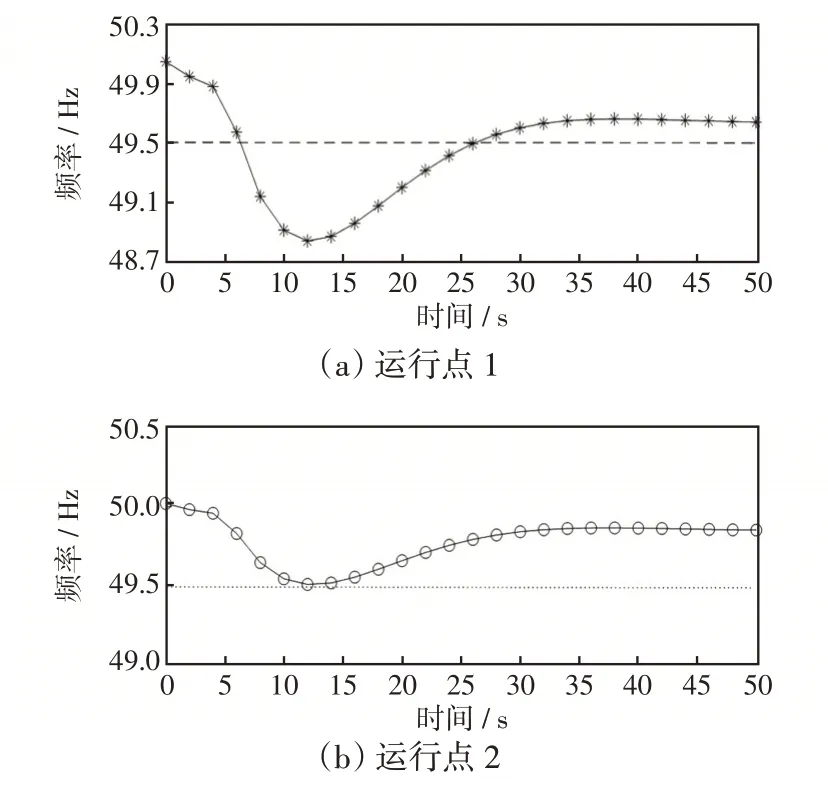
图7 不同惯量水平下频率响应Fig.7 Frequency response under different inertia levels

3.3 不同渗透率下频率响应曲线

随着渗透率水平的不断提高，越来越多的同步机组被新能源机组替换，这导致系统内的同步惯量降低，故频率稳定性也逐渐降低，不同渗透率下的惯量水平如表3所示。

表3 惯量水平Tab.3 Different inertia levels

不同渗透率下的频率响应特性如图8所示。在107.4 MW的功率波动下，最大频率变化率为0.25 Hz/s，惯量最小需求为21 480 MW·s。

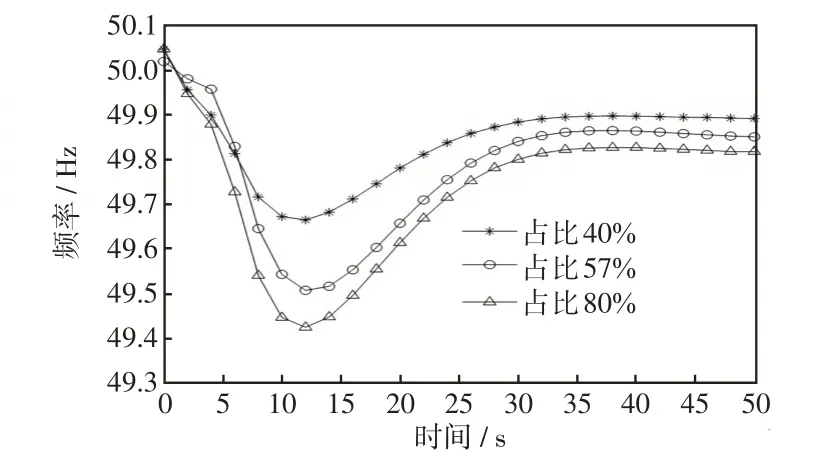
图8 不同渗透率下的频率响应Fig.8 Frequency response under different penetrations

分析表3和图8可知，随着渗透率的不断增加，系统的惯量水平会逐渐降低，当新能源占比40%时，此时系统的惯量水平为34 828.8 MW·s，满足设置的波动下的最小惯量需求，此时，频率最低点未触发低频减载动作；当新能源占比为57%，系统的惯量水平仍然在可行区间内，满足最小惯量需求；当新能源占比为80%时，此时系统的惯量水平为11 609.6 MW·s，已达不到系统频率稳定的最小惯量需求。

经对比分析可知，新能源渗透率的提高直接导致系统的惯量水平降低，使得系统运行点位于可行区间外，此时不提供虚拟惯量支撑，将会发生频率稳定问题。

4 结语

随着高渗透率可再生能源的不断接入，电力系统的惯量水平不断降低，一旦发生大的扰动，很容易触发安稳动作，这不利于系统的频率稳定性。

本文首先理论推导新能源场站和储能系统的等值惯性常数，充分利用可控元件来提高电力系统的频率稳定性。然后基于RoCoF约束和频率最低点约束获取最小惯性需求，构建惯性可行区间，将同步机惯量和虚拟惯量相结合，从而判断系统运行点是否满足频率安全约束，可为调度人员提供直观的展示。最后经仿真分析可知，系统的惯量不足会导致系统在功率较大波动时触发低频减载或高频切机等安稳动作，如不加以控制，会导致范围更大的频率稳定问题。