含可再生能源的多区域电力系统负荷频率控制

关燕鹏，李晓宁，贾新春

（山西大学自动化与软件学院，太原 030006）

多区域电力系统是在综合考虑电力市场经济效益和负荷分布情况后进行区域划分，然后通过输电线将各区域互联形成的[1]。这种互联形式的电力系统的各区域之间可以互相提供功率支持，进而有效地解决能源和负荷分布不均的问题，优化资源配置，节省电力交易费用。因其在经济性和可靠性上都具备一定优势已成为现代电力系统发展的重要趋势。但互联也使得电力系统更加复杂，任何区域扰动引起的振荡都可能扩散到其它区域，导致系统停电[2]。

多区域电力系统的成功运行需要系统发电机组的总发电量与电力负荷的总需求量以及相关的系统损耗之间保持平衡[3]。可以在电力系统中引入负荷频率控制LFC（load frequency control）来实现这一目标，LFC能够在负荷发生变化及存在外部扰动的情况下，将各区域的频率和它们之间联络线交换功率保持在设定范围。近年来，LFC已成为保障多区域电力系统输出稳定可靠电能的重要手段。

在低碳发展和能源结构优化的大背景下，以化石能源等作为电力来源的传统发电技术，造成的能源安全和气候变化等问题受到各国的日益关注。人们正在寻求新的发电技术，其中风力发电、太阳能发电等可再生能源RESs（renewable energy sourc⁃es）发电技术已被成功应用到现代电力系统中。但RESs发电机组接入的比例越大，电力系统的总惯量就越小，LFC将更具挑战性[4]。一方面，系统惯量越小，对系统提供的阻尼就越小，系统对发电和负荷模式下突变反应表现过于强烈，不利于系统恢复稳定[5]。另一方面，传统的LFC大多采用PI控制，但是RESs具有较强的间歇性，会产生随机波动性扰动。因此，为了解决上述问题，研究者利用储能系统以及电力电子逆变器加上适当的控制机制构成虚拟同步发电机，在电力系统中模仿常规同步发电机的行为，并为系统提供辅助控制作用，以增加系统的惯量，提高系统的稳定性[6]。目前，大多数虚拟惯量研究只停留在单个区域电力系统中，而将虚拟惯量技术引入含RESs的多区域电力系统中具有很好的前景。

另外，在目前的多区域电力系统中，为了实现对各区域的稳定控制，大多采用分散式控制结构。这种控制结构在每个区域都设置子控制器收集局部信息做出局部决策。即使整个系统具有一个总体的控制目标，每个子控制器节点也不与附近节点共享信息。控制器之间缺乏通信和协作，这可能只能实现次优控制性能[7]。并且在大型电力系统中的区域间振荡通常无法通过分散式结构来控制[8]。因此，如果允许子控制器之间互联共享局部信息，实现协同控制，将有望提高整个电力系统的控制性能[9-10]。但在上述文献中研究者们在所有子控制器之间都建立了通信信道，这种方法在实践中往往是不必要的。一方面，这会导致不必要的信道设置，增加建筑成本。另一方面，使用的通信信道越多，系统的信息就越容易受到恶意攻击。因此，如何在控制器间建立较少的通信信道，增强区域间的协同控制作用，以应对RESs接入后对系统的影响是本文讨论的另一问题。

上述问题实际上是一个稀疏优化问题，目前，已经有文献提供了一些解决这一问题的方法[11-15]。如利用交替方向乘子法在优化闭环系统性能和提高反馈增益矩阵稀疏性之间进行交替优化处理[11]。基于l1范数进行迭代，通过对矩阵不等式中的耦合项进行分解来提高状态反馈增益矩阵的稀疏性[12]。文献[14]将结构稀疏性的概念加入到网络控制系统设计中，利用l1和l2范数的组合惩罚目标函数得到结构稀疏性。文献[15]使用特殊矩阵范数对稀疏优化问题进行凸化，获得次优解决方案，进而构造行稀疏反馈增益矩阵，设计稀疏控制输入。其中，文献[11]提出的交替方向乘子法在文献[16]已被成功用于多区域电力系统分布式最优LFC的设计中。上述文献提及的方法大多需要复杂的迭代求解过程，而本文采用的基于混合整数规划的方法则更为简单。我们事先限定控制器间信道的具体数目，让系统在使用少量信道的情况下，就能够稳定运行。另外，将信道的数目等价为控制增益矩阵K中耦合项K ij不为零的个数，然后利用混合整数规划的方法对增益矩阵K进行势约束，进而实现控制器间通信信道数目的稀疏优化。

在传统LFC中，通常采用专用的通信链路进行数据传输。这种专线通信方式造价高昂、维护困难，不适合在跨区域互联电力系统中使用，已被开放的网络通信方式所取代[17]。但网络通信系统存在带宽约束，若采用周期通信机制往往会传输大量冗余数据，造成通信和计算负担，可能导致电力系统故障。因此，需要在网络化LFC中引入事件触发通信机制，使采样数据只有在满足一定条件时才进行传输，减少对网络带宽的不必要利用，节约有限的资源。

综上，为应对RESs接入多区域电力系统后造成的系统惯量减小问题，本文在传统LFC的基础上添加基于虚拟惯量技术的微分控制回路对多区域电力系统中储能系统的有功功率进行控制，模拟惯量功率，产生惯量特性，提高含RESs的电力系统的总惯量；为应对由于RESs间歇性造成的随机波动，将区域的子控制器按稀疏优化的结果部分互联，实现分布式协同控制，提高LFC性能。

1 问题描述

1.1 含RESs的多区域电力系统LFC模型

本文研究的多区域电力系统采用全耦合网状拓扑结构，各区域通过联络线两两互联，进行电力输送，如图1所示。尽管采用这种结构的多区域电力系统是一个强耦合时变系统，但LFC是针对波动较小的扰动提出的，此时系统基本工作在稳定点附近，因此可以采用低阶线性传递函数对其建立模型[18]。

图1 4区电力系统物理连接拓扑Fig.1 Physical connection topology of 4-area power system

本文以传统火电机组为基础建立含RESs的多区域电力系统LFC模型如图2所示，在进行详细推导前对该模型进行以下说明。

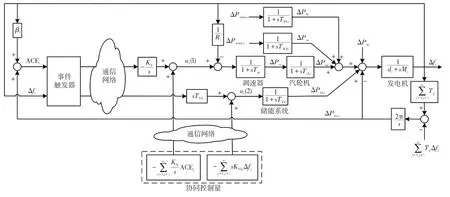
图2 含RESs的多区域电力系统中第i个区域的LFC模型Fig.2 LFC model for the i th area in multi-area power system with RESs

（1）多区域电力系统LFC的目标是将系统频率和区域间联络线功率控制在正常范围内。基于上述目标，通常将频率偏差Δf(t)和联络线功率偏差ΔPtie,i(t)线性组合形成一个称为区域控制偏差ACE(t)的变量，作为LFC问题中的控制信号，并将ACE(t)为零作为衡量控制区域实现稳定的标准，则第i个区域的区域控制偏差ACEi(t)可定义为

式中：βi为频率偏差系数；Δf i(t)、ΔPtie,i(t)分别为第i个区域的频率偏差与联络线偏差。

（2）传统火电机组LFC系统由调速器、非再热汽轮机、发电机-负荷、联络线及控制器等元器件构成，各区域的元器件均采用单机模型等效多机动态响应，当某区域负荷发生变化或存在外部扰动时，控制器接收控制输入信号，发出控制指令改变调速器阀门位置，调节流入汽轮机的蒸汽量，进而改变汽轮机的输出功率，影响发电机的输入功率，调整发电机的有功出力，完成控制目标。

（3）在传统LFC基础上增加基于储能系统的虚拟惯量控制环节，通过储能系统的有功功率由系统频率的微分控制，虚拟模仿惯量功率，将有助于提高RESs接入后的系统惯量。另外，各区域接入的RESs发电机组产生的发电量在满足该区域设定负荷需求量后，多余部分被视为能量有界的外部扰动信号。为抑制这部分随机性扰动，按稀疏优化的结果将部分控制器互联共享协同控制信息形成分布式结构，系统通过主动调节火电机组和虚拟惯量控制环节来抑制负荷变化和随机扰动。

图2 描述的模型可以用微分方程表示为

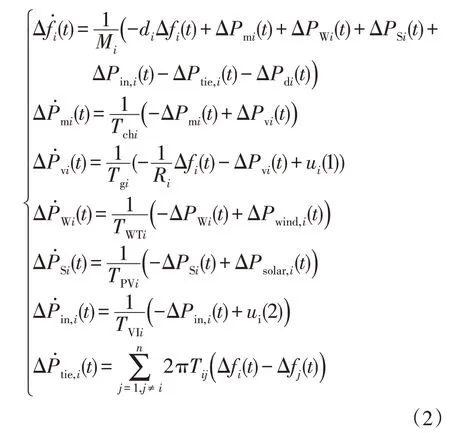
式中：Δf i、Δf j为频率偏差；ΔPmi为发电机输出功率偏差；ΔPvi为调节阀位置偏差；ΔPWi为风能功率偏差；ΔPSi为太阳能功率偏差；ΔPin,i为储能系统的虚拟惯量功率偏差；ΔPtie,i为联络线有功功率偏差；ΔPdi为负荷扰动；ΔPwind,i为风电场扰动；ΔPsolar,i为太阳能电场，ACEi为区域控制偏差。Mi、d i分别是发电机惯性常数和阻尼系数，Tchi是汽轮机时间常数，Tgi是调速器时间常数，Ri是下垂特性参数，TWTi是风力涡轮机时间常数，TPVi是太阳能发电系统时间常数，TVIi是虚拟惯性时间常数，T ij是同步系数。

选取Δf i,ΔPmi,ΔPvi,ΔPWi,ΔPSi,ΔPin,i,ΔPtie,i,∫ACEi为子系统i的状态变量，则根据式（1）~（2）可知如图2所示的含RESs的多区电力系统的LFC状态空间表达式为

其中，

βi为频率偏差系数，

本文增加基于微分技术的虚拟惯量控制环节u i(2)，通过调节储能系统，增强系统惯量。另外将部分控制器互联形成分布式结构，实现协同控制以应对各种随机扰动。各区域控制输入形式为

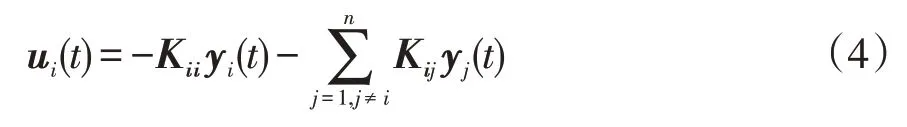
式中，y i(t)与y j(t)分别为区域i与j的系统输出，K i i为区域i固有控制增益矩阵，K i j为区域i与j协同耦合增益矩阵。若K i j不为零，表示存在信道使得区域i可以接收来自区域j的协同控制信息。本文的一个目的是在控制器之间建立尽可能少的通信信道使得系统达到期望的控制性能。为此，给出以下约束条件：

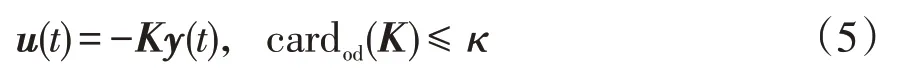
式中，整数κ满足0≤κ≤n(n-1)，

cardod(K):=K中非零K i j的数目，i≠j。

1.2 分布式事件触发传输机制

本节引入一种分布式事件触发传输机制，以减少不必要数据包的传输，节约有限的传输资源。假设D≡0,即外部扰动不影响系统输出值。则从图2中，可以看到带有零阶保持器的LFC的输出为

式中：是区域i的上一次控制信号传输时刻；为该时刻传输数据。事件触发阈值条件为

式中：Φi＞0为加权矩阵；δi∈(0,1)是事件触发阈值参数，i=1,2,…,n；h为采样周期；为当前采样数据与最近传输数据之间的误差，其表达式为

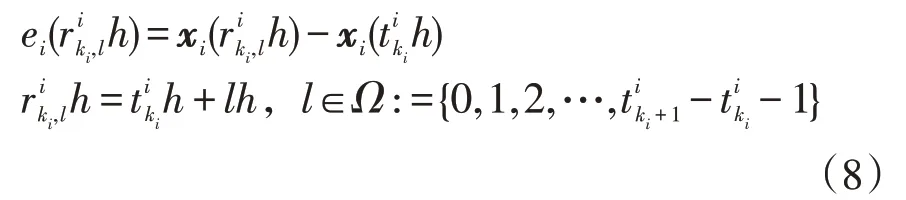
用式（6）代替触发阈值条件式（7）中的输出项可得

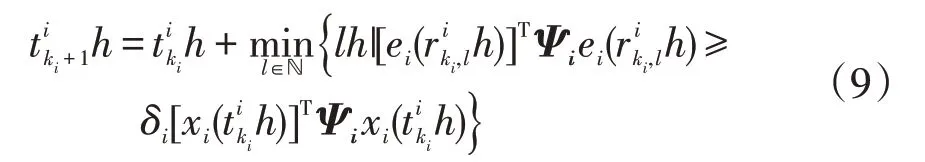
式中，Ψi=，只有当满足阈值条件式（9）时才将采样数据通过通信网络进行传输。

将式（6）代入式（4）得

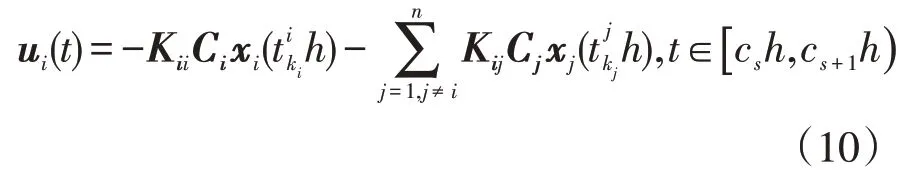
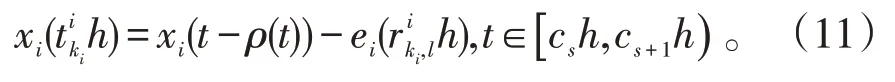
由此可知，采用分布式事件触发通信机制的多区域电力系统的LFC闭环系统可以表示为

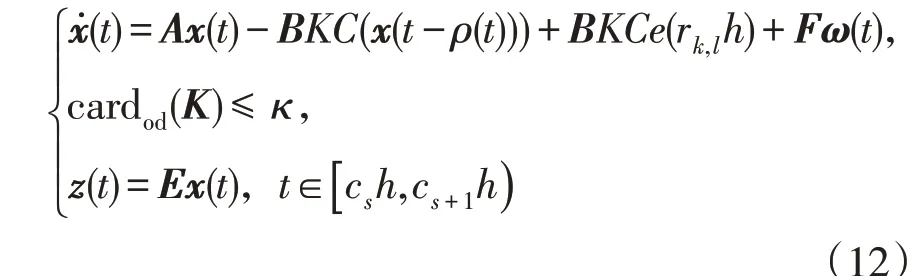
本文的最终目的是设计分布式最优LFC策略使得系统式（12）H∞指数稳定，即满足如下两个条件：

（1）当外部扰动ω(t)=0，系统式（12）呈指数渐近稳定；

（2）零初始状态下，对所有非零扰动ω(t)∈L2[0,∞)和一个正标量γ，不等式（13）成立。

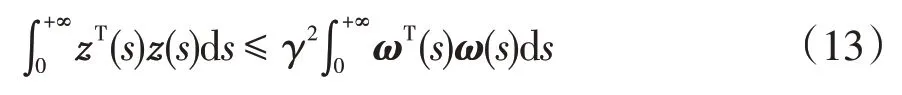
2 主要结果

针对含RESs的多区域电力系统LFC问题，应用李亚普诺夫稳定性理论，首先给出闭环系统式（12）的稳定性条件，再获取分布式稀疏控制器式（5）的设计方法。

2.1 H∞稳定性分析

定理1：给定标量α＞0，γ＞0，控制策略式（10），事件触发机制，若存在矩阵P＞0，Q＞0，R＞0，以及矩阵Y，使得不等式（14）~（15）成立，则闭环系统式（12）H∞指数稳定。

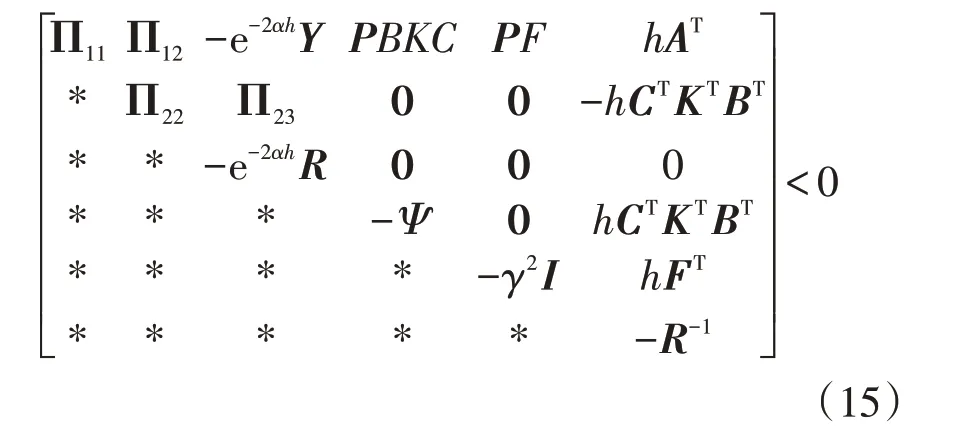
式中，Π11=P A+A T P+2αP+Q-e-2αh R+E T E，Π12=e-2αh(R+Y)-PBKC，Π22=-e-2αh(2R+Y+Y T)，=diag{δ1Ψ1,δ2Ψ2,…,δnΨn}，Π23=e-2αh(R+Y)。

证明：选取以下正定Lyapunov-Krasovskii泛函为

式（16）关于时间t求导可得

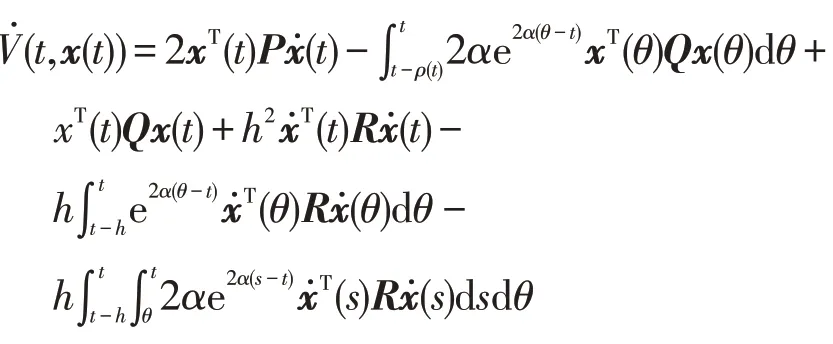
根据文献[19]中的引理1可得

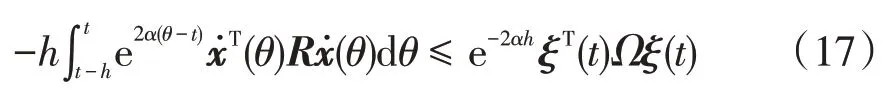
其中，

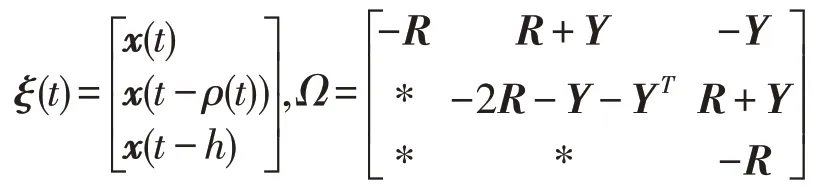
通过计算̇(t,x(t))+2αV(t,x(t))，结合Schur补定理可知，如果式（14）成立，则

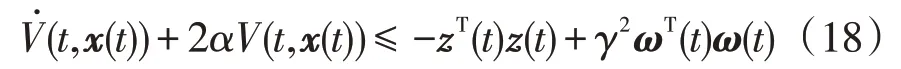
从而可知闭环系统（12）H∞指数稳定，证毕。

2.2 分布式稀疏结构控制器设计

各区域的子控制器间实现稀疏互联对抑制RESs带来的随机扰动具有重要意义，然而稀疏优化问题的求解是困难的。通过式（5）已将这一问题转化为对系统控制增益矩阵K的势约束问题，下面给出利用混合整数规划求解的具体方法。

定理2：给定一个足够大的正数M使得‖K‖max≤M，若存在一组二进制数y ij∈{0,1}能使式（18）成立，则势约束cardod(K)≤κ成立。

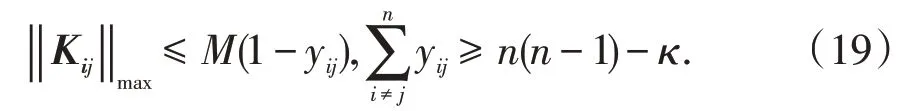
定理3：给定α＞0，γ＞0，s＞0，δi∈(0,1)，以及整数κ，若存在正定矩阵，矩阵正数M，以及二进制数yij∈{0,1},i≠j,使得不等式（20）~（22）成立，则系统H∞指数稳定，并且系统的控制增益K=VU-1，满足cardod(K)≤κ。

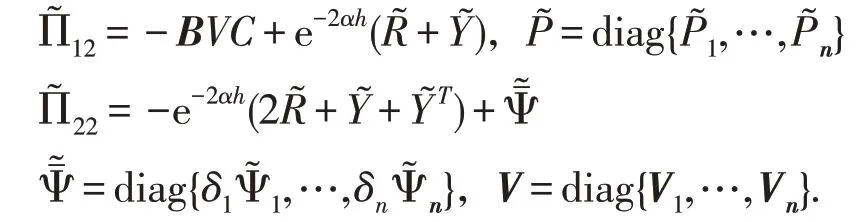
定义V C=͂，U C=͂，将其转化为文献[20]中的W-problem。由于C是行满秩矩阵，由UC=͂，͂＞0可知U也是满秩可逆矩阵，所以K=VU-1。

根据定理2及矩阵结构可知，如果式（22）成立，则K满足稀疏约束条件，cardod(K)=cardod(V)≤κ。

利用(U C-͂)T(U C-͂)＜εI，可将等式约束转换为中右边不等式。证毕。

3 仿真实例

本节将利用一个含RESs的4区互联电力系统来验证所提的LFC设计方法的有效性，各区域的参数值如表1所示[21]。

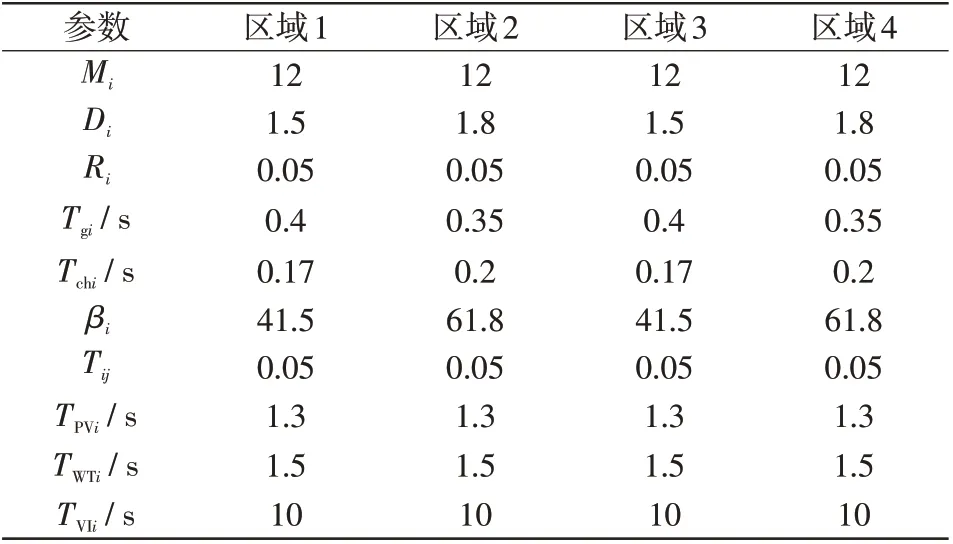
表1 含RESs的4区电力系统参数Tab.1 Parameters of 4-area power system with RESs

选取采样周期h=0.01 s，指数衰减速率α=0.01，H∞性能指数γ=150，控制增益矩阵的边界M=106，各区域的事件触发阈值参数分别为δ1=0.01，δ2=0.02，δ3=0.01，δ4=0.02，当κ=2时，应用YALMIP求解式（20）~（22），可解得具有稀疏结构的K为

其中，

在电力系统运行过程中，4区电力系统的负荷变化与风力发电及太阳能发电带来的扰动如图3和图4所示。

图3 区域1和区域2电力系统扰动Fig.3 Disturbances in the 1st-and 2nd-area power systems

图4 区域3和区域4电力系统扰动Fig.4 Disturbances in the 3rd-and 4th-area power systems

采用求解的K矩阵作为系统输出反馈控制策略的增益矩阵，在零初始条件下，得到的系统响应如图5与图6所示。各区域的控制数据事件触发时刻如图7与图8所示。

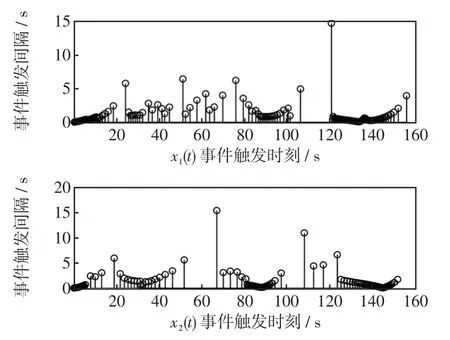
图7 区域1和区域2电力系统事件触发传输时刻Fig.7 Event-triggered transmission time of the 1st-and 2nd-area power systems

图8 区域3和区域4电力系统事件触发传输时刻Fig.8 Event-triggered transmission time of the 3rd-and 4th-area power systems

由以上的仿真结果可知，cardod(K)=2，K13与K14矩阵不为零，这意味着区域1电力系统的控制器与区域3、区域4电力系统的控制器之间存在通信信道，使得区域1的控制器可以接收来自区域3、区域4的控制信息，以提高本区域的控制性能。另外，从图5及图6中可以看出，电力系统在负荷发生变化或RESs发电带来扰动时，各区域的频率跟联络线功率都会偏离设定值。通过采用本文提出的控制策略，系统式（12）的频率偏差Δf i(t)与联络线偏差ΔPtie,i(t)最终都趋于零。说明本文提出方法可以有效实现LFC的主要目标。在仿真时间T=160 s期间系统共采样16 000次，但各区域的数据传输次数仅分别为217，177，486，486，这意味着可以节约相当量的传输资源。

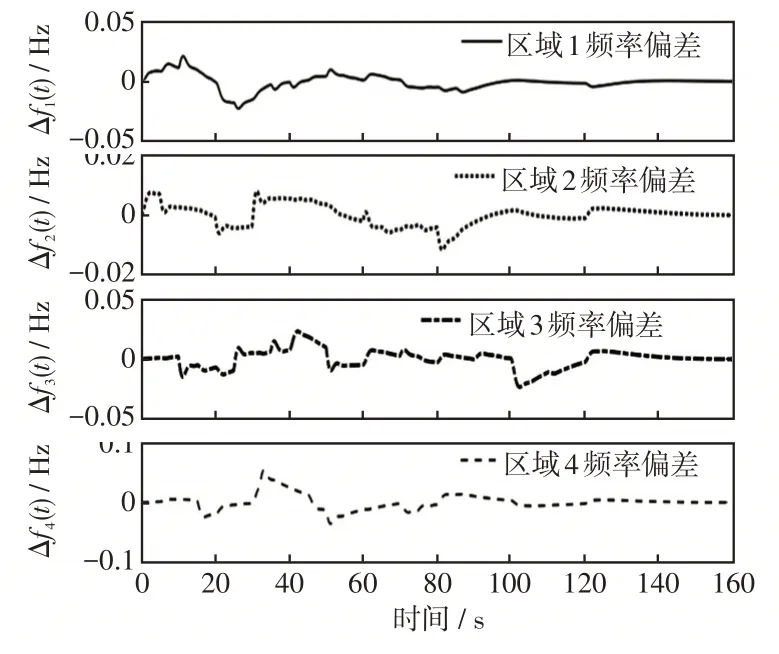
图5 系统频率响应Fig.5 Frequency response of system

图6 系统联络线功率响应Fig.6 Tie-line power response of system

4 结语

本文通过改进传统的LFC系统的模型，来应对RESs发电机组接入电力系统后带来的负面影响。通过增加基于储能系统的虚拟惯量控制环节来解决系统惯量减小的问题，根据混合整数规划法求解的稀疏优化结果实现区域控制器间的稀疏互联以应对RES带来的随机性扰动。应用李雅普诺夫稳定性理论和一些矩阵运算技巧得出系统稳定条件和稀疏结构控制器的设计方法。最后，通过一个4区电力系统验证了该方法的实用性。