钻芯法检测中混凝土抗压强度推定关键问题研究
2022-08-01朵润民陈仁进梅莉莉
朵润民,陈仁进,梅莉莉
(1、广东省建筑设计研究院有限公司 广州 510145;2、广东粤信建设工程质量安全检测有限公司 广东 东莞 523220;3、河南省建筑工程质量检验测试中心站有限公司 郑州 450000)
0 引言
混凝土强度是混凝土质量控制的必要参数,通常采用同条件养护试块和标准养护试块的压力试验来确定。当试块无效或对混凝土质量质疑时,成型后的混凝土构件抗压强度检测就非常重要,实体混凝土抗压强度的检测还是一些地区质量验收的必要程序。其中,钻芯法作为一种直接检测法,被广泛应用。它不仅可以直观地反映混凝土强度,也可作为其它无损检测的修正,在工程检测上无可替代[1-3]。
对于同一批混凝土构件的强度检测,可采用钻芯法进行批量评定,通过混凝土强度推定值和混凝土强度设计值的比较,来判定该批构件混凝土强度的符合性。目前,混凝土强度推定值的计算普遍采用三种方法,即《钻芯法检测混凝土强度技术规程:JGJ∕T 384—2016》[4]和《建筑结构检测技术标准:GB 50344—2019》[5]、《民用建筑可靠性鉴定标准:GB 50292—2015》[6]、《水运工程混凝土结构实体检测技术规范:JTS 239—2015》中所论述的推定方法[7]。文献[4]和文献[5]是较为常用的推定方法;《水运工程混凝土结构实体检测技术规范:JTS 239—2015》主要在水运工程中使用,推定值与前者结果相当;文献[6]主要应用在既有结构的混凝土强度推定中,推定值偏低,部分情况下可能小于抽检芯样强度的最小值。
然而,混凝土强度可否推定需满足较为严苛的条件,大部分情况下将不具备推出条件,即使采用《数据的统计处理和解释正态样本离群值的判断和处理:GB∕T 4883—2008》[8]也很难剔除异常值。对于一些既有建筑,不得不使用文献[6]中的推定方法,导致结构后期加固量增加。
本文从混凝土强度推定值的概念入手,探讨通用推定方法的局限性和弊端;结合实际工程的概率统计,研究可能导致无法推定的原因;探讨无法推定时,异常值剔除的可能性。提出满足规范推定条件的合理化建议。
1 强度推定值的概念和推出条件分析
强度推定值是指混凝土强度分布中的0.05 分位值的估计值,即95%保证率分位值的估算值。强度等级是按照95%保证率的立方体抗压强度标准值进行划分的。两者具有一一对应的关系,通常以推定值与设计强度等级的比较来作为混凝土强度的符合性判定依据。需要注意,平均值是0.5 分位值,最小值非0.05分位值,理论上无法作为强度等级评定的依据。
强度推定值是估计值,属于随机变量,只能通过给定的置信水平确定其置信区间,本文采用0.85 的置信水平进行讨论。混凝土强度值符合正态分布,此时混凝土推定值符合非中心t分布函数[9]。文献[5]给出了非中心t分布函数下的置信区间推定上限值H和下限值L,其代表的数学含义是:该批混凝土至少有95%的混凝土强度高于推定上限值H的事件的置信度(可靠度,下同)为0.05,该批混凝土至少有95%的混凝土强度高于推定下限值L的事件的置信度为0.90[10]。规范将推定上限值作为混凝土强度推定值,根据《正态分布完全样本可靠度置信下限:GB∕T 4885—2009》查表可得,当采用推定上限值作为混凝土强度推定值时,只能保证该批构件至少有74%~90%的混凝土强度高于推定值H的事件的置信度为0.90,具体如表1所示。理论上,推定上限值H大于强度标准值,推定下限值L才接近强度标准值。文献[10]也对取推定上限值提出质疑,建议置信度取0.50 确定混凝土推定值。实际操作过程中,由于钻芯法检测的不确定因素较多,计算标准差s往往偏大,导致推定上限值可能更接近于强度标准值,推定下限值反而偏小。文献[10]采用推定上下限差不大于5 MPa 和0.10 倍的推定上下限值平均值两者的较大值来控制标准差的偏离。这样推定值的误差也控制在一个强度等级内,对于结构安全来说属于可控范围。

表1 不同置信度下的混凝土强度保证率Tab.1 Guaranteed Rates of compressive Strength of Concrete with Different Confidence
文献[6]采用置信度为0.90 的推定下限值L作为混凝土强度推定值,未给出推定上限值H,采用变异系数不大于0.20 的条件限制标准差的偏离。两种方法标准差s限制条件的对比如表2 所示,当强度平均值大于强度分界线时,文献[6]条件更加宽松。若某检验批标准差不满足文献[5]的要求而满足文献[6],标准差偏大较多,推定下限值L将降低很多。文献[6]的推定方法显然不够合理,应尽量避免使用。此时,应着手分析和解决标准差过大的原因,可采用增加抽样数量、频数分布图分析、异常值剔除等方法改善标准差的偏离,下文将具体进行讨论。对于既有建筑的验算,应综合分析混凝土强度、结构复核验算情况和现场检测情况,采用合理的强度值进行验算。
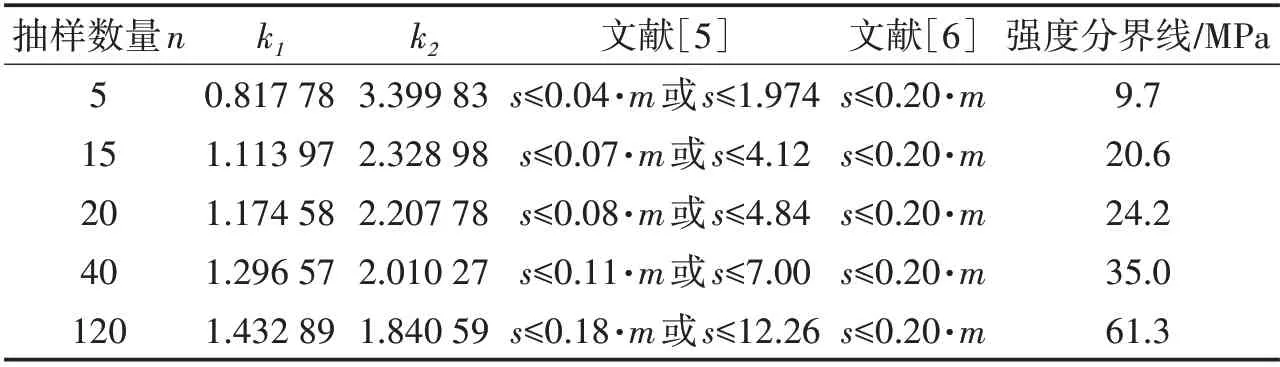
表2 文献[5]和文献[6]标准差限制条件对比(m为平均值)Tab.2 Comparison of Limitation Factor of Standard Deviation between Reference[5]and Reference[6](m is the Average Value)
2 频数分布图分析法
同一批混凝土强度符合正态分布,强度推定值的计算方法是根据正态分布函数推导而来。混凝土强度可以推定的基本要求是抽检的芯样抗压强度应总体上符合正态分布规律,否则该方法计算出的强度推定值将严重失真或标准差过大。频数分布图是研究随机变量分布规律的基本方法,通过频数分布图可分析检测数据可能出现的失真原因,为检测单位改善抽检方法、改进检测能力提供依据。
频数分布图分析案例如图1 所示,正态分布曲线是由抽检样本强度的平均值和标准差画出。通过条形图的集中性、对称性和均匀变动性与所求得的正态分布曲线对比,评价检测数据是否失真。案例1 条形图的高点及变动性与所得正态分布曲线基本一致,此时推定值上下限差满足规范要求,强度可推定;案例2条形图的分布与所得正态分布曲线不符,此时推定上下限差大于规范值,强度不可推定。由于条形图分布较为分散,频数相当,数据失真严重;案例3、案例4 的检测数据来自同一家单位,案例3可推定,案例4不可推定,但可发现条形图对称性差,同一批构件低强度构件数量偏多,说明存在系统误差,该单位在样品采集、运输、试验过程中存在一定的漏洞,应积极排查改进;案例5仅抽检5个芯样,无法判定其是否来自与总体正态样本,推定上下限差较大;案例6条形图有两个较为明显的波峰,通过原始数据核查可以发现,两个波峰区域的数据分别来自于同一层不同区域,此时应考虑该层混凝土属不同批次,核查是否存在施工缝等,重新划分区域后分别评定。
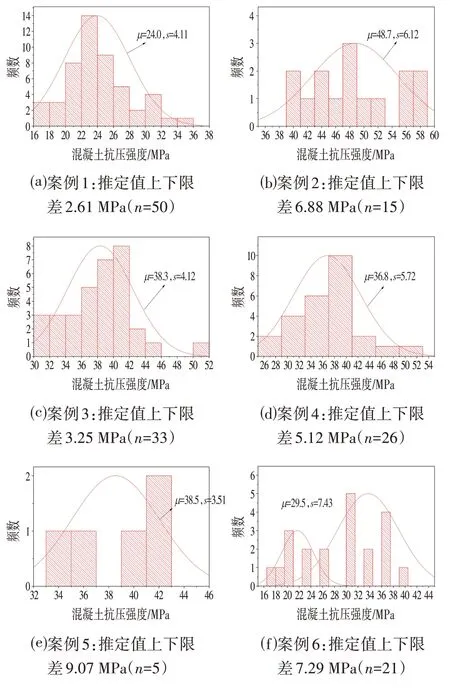
图1 频数分析案例Fig.1 Frequency Analysis Case
通过上述案例可以看出,频数分析法不仅可以判断检测数据的失真程度,分析标准差异常的原因,还可以分析数据真伪和判断单位钻芯检测能力。案例8可以看出,抽检数量偏低时,较难形成有效的正态分布,即使可以推定,推定值也处于失真状态。因此,文献[4]规定的最小抽检数量有一定的依据,实际检测过程中建议抽检数量不少于15个芯样。实际使用过程中,可采用峰度和偏度进一步量化上述分析[11]。
3 异常值剔除的分析
当标准差不满足文献[4]和文献[5]的要求时,建议采用文献[8]进行异常数据的剔除。总体方差未知时,文献[8]给出了格拉布斯检验法、狄克逊检验法、偏度-峰度检验法3 种方法。在出现多个异常值的时候,重复使用同一检验法可能出现判多为少和判少为多的错误,重复使用偏度-峰度检验法出现两类错误的概率较小,重复使用狄克逊检验法效果次之,重复使用格拉布斯检验法效果最差,因此优先建议采用峰度-偏度法[12]。峰度-偏度检验法是正态性检验的优良检验法,不来自正态分布的样本都可能被它拒绝。使用偏度-峰度检验法时,应先依据《数据的统计处理和解释 正态性检验:GB 4882—2001》判断数据的正态性,条件较为苛刻。在样本数据不满足正态性时,宜采用狄克逊检验法,狄克逊检验法将样本数量限制在30个以内,仍具有局限性。
以案例1 和案例2 进行分析,检出水平α=5%,采用双侧情形研究剔除大值的情况,如表3 所示。通过上文可知,案例1已满足推定要求,采用异常临界值代替样本最大值后,推定上下限差仍满足规要求,说明异常值的剔除可有效解决无法推定的问题;案例2 已不满足推定要求,采用三种检验方法均不能筛查出异常值。两者的区别是:案例1 条形图基本符合正态分布,样本频数与所计算出的正态分布曲线基本一致;案例2 不符合正态分布,计算出的正态分布曲线并不能代表总体样本的正态分布曲线,标准差较大导致异常临界值偏大,异常值难以筛查。因此,是否能采用文献[8]进行异常数据的剔除的前提条件是抽检样本的频数分布图基本符合正态分布的要求,数据无失真现象。

表3 不同检验方法对比Tab.3 Comparison of Different Test Methods
4 满足正态性的办法
综上所述,频数分析法是解决钻芯法检测强度无法推定的重要工具,抽检样本数据基本满足正态性时,异常值剔除才会真正有效,这也是抽检数据不失真的前提条件。因此,混凝土强度推定值计算的本质在于使抽检样本的频数分布符合正态分布,且该分布能代表总体样本的分布情况,任何不满足正态性的推定值均是失真的。仅通过数据处理是无法有效解决非正态性问题的,应从检测的抽样方法、抽样数量、试验等方向解决该问题:
⑴抽样数量建议不少于15 个构件,抽样数量越少代表性越小,样本正态性越差。在无法推定的情况下,增加抽检数量具有一定的作用。同批构件抽样位置的选取应尽量分散。
⑵抽样过程和运输过程应减少样品的扰动,合理控制钻芯速度;应定期检查钻芯机的稳定性。芯样的质量应严格按照规范要求筛查。
⑶应严格按照高径比、垂直度、平直度控制加工后的芯样质量,排除可能影响结果的一切因素,如含水率、端面补平等;
⑷建议同批构件由同一试验设备、同一试验人员进行操作,减少随机因素造成的不确定性;
⑸ 可通过频数分析解决试验时普遍存在的问题:同批构件低强度芯样总是偏多,应分析任何导致检测强度偏低的客观因素,芯样未处理端面、不在干燥状态下试验等;同批构件高强度芯样偏多,压力机的试验速度是否过快等;
实际情况下,影响钻芯结果的因素远多于回弹法,采用回弹钻芯修正的方法可减少这些方面的影响,更容易得出混凝土强度推定值。对于既有建筑的鉴定,当检测条件限制导致标准差偏大时,采用文献[6]推定值将过于保守,采用最小值作为推定值可接受,但仍可能较为保守[13]。因此,需结合现场实际使用情况,结合荷载试验等方法综合判断。
5 结论
⑴抽检样本的正态性是混凝土强度能否推定和异常值能否剔除的前提条件,是推定值计算公式的推导前提;
⑵频数分布图是分析抽检样本的正态性的有效工具,它是通过条形图的集中性、对称性和均匀变动性与所求得的正态分布曲线对比进行分析的。通过频数分析,可得到检验批划分的合理性、检测数据的异常情况等结论,为推定值、异常数据的剔除、试验方法的改进提供依据;
⑶仅通过数据处理、数据剔除无法有效解决检测数据的非正态性问题,应从抽样方法、抽样数量、试验条件方面解决该问题;
⑷既有建筑推定值的取值不能盲目采用规范取值,应结合现场实际使用情况,合理化取值。
