无人机自主着舰技术研究

刘 丰，于 洋，郭 璇,*，毕卫红，高佳玥

(1. 燕山大学 信息科学与工程学院，河北 秦皇岛 066004； 2. 河北省特种光纤与光纤传感重点实验室，河北 秦皇岛 066004)

0 引言

随着我国海洋强国战略的推进实施，构建遥感卫星、无人机、无人艇、海面站、岸基站一体的海洋立体生态监控网络体系是推进我国海洋生态文明建设、保护海洋环境所急需的关键技术。特别是随着我国无人机技术的迅速发展，基于无人机的近岸海域绿潮、赤潮等生态灾害的实时监测技术已经成为海洋科学领域的研究热点。在海洋灾害监测中可用的无人机系统资源越来越丰富，搭载的专用设备的性能和系统智能化程度也在不断提高[1]。无人机监测作为传统监测手段的重要补充，在灾情监测中表现出了效率高、行动迅速、监测细致等优势[2-3]。

然而，目前无人机受限于持续续航能力不足，导致岸基起飞覆盖监测面积受限，限制了无人机在海洋环境监测领域的深度应用。开展无人机自主着舰技术的研究是拓展基于无人机的海洋藻类灾害监测范围、保障无人机飞行安全、甚至实现无人机着舰电力自动补充的核心技术之一。GPS导航是目前最为广泛使用的无人机定位技术[4]，然而在GPS导航系统精确度不高的情况下，现有的惯性导航系统在误差补偿时不能提供足够精确的位置信息,难以胜任自主着陆的要求,所以要另外寻求其他的有效手段[5]。

在无人机自主着陆技术领域，针对静态着陆点降落已有较为完善方案，技术也趋于成熟。文献[6]和[7]设计了一套辅助无人机自动着陆的机器视觉系统，对水平地面上的着陆点进行检测。而对于随海面波动实时变化的无人艇着陆平台来说，平稳安全着陆依旧是个未得到良好解决的难题。文献[8]通过采用地面人工标识April Tag与无人机的视觉引导跟踪算法相结合的方案，实现无人机的悬停和在移动平台上的着陆，但对于起伏不定的无人艇，无法保证能够安全着陆。文献[9]针对无人机在垂直升降平台上的自主着陆问题，设计了由运动估计模块、轨迹生成模块和跟踪模块组成的控制结构，但对于存在倾角的着陆面未进行实验分析。

本文针对无人机自主着舰技术的实际工程需求，提出了基于机载摄像头与艇载惯性导航装置相结合的自主降落方案。通过对降落标志的识别，结合无人艇传回的姿态数据，对着舰的最佳时机进行判定，以实现无人机的安全着舰。经过理论建模分析和实验研究表明本方案能够实现无人机在无人艇上的自主安全降落，研究结果能够为无人机自主在无人艇上可靠着陆提供理论支撑，并具有很好的实际工程应用价值。

1 无人机自主着舰控制方案

本文研究的四旋翼无人机自主着舰系统流程如图1所示。

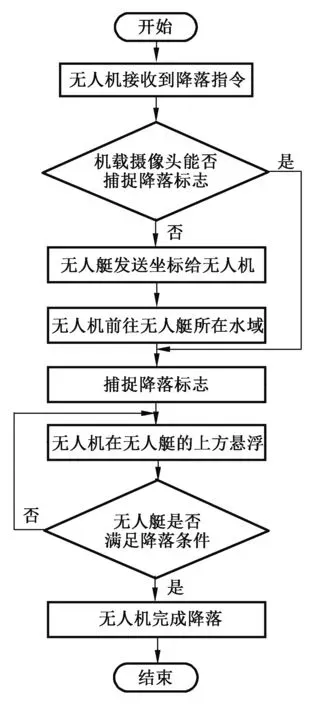
图1 无人机自主着舰策略Fig. 1 Autonomous landing strategy of UAV

在无人机的着舰过程中，通过能否捕获降落标志来判断无人机与无人艇是否在同一水域。若不在同一水域，无人机通过GPS导航向无人艇方向进行移动。

因为无人艇随海浪的波动会进行无规则的运动，导致无人机无法直接在无人艇上进行降落。影响无人机降落的两个主要参数是滚转角和俯仰角[10]。为了降低无人机视频图像识别处理的难度，本方案通过在无人艇上搭载惯性导航单元来获取实时滚转角和俯仰角信息，并通过短距无线通信系统实时传输到无人机控制系统，当无人艇的姿态满足无人机降落条件时进行着陆操作，否则在当前位置进行悬停，重新寻找下一次降落的最佳时机。

1.1 降落平面检测系统

本文所设计的降落平面检测系统包括两部分如图2所示，安装于降落平面上的为测量发送设备，以MPU6050为核心，实时检测平面的姿态信息，并利用无线传输模块，将姿态信息发送出去。安装于四旋翼无人机上的为决策接收设备，接收到测量设备传回来的姿态信息，对此时降落平面的姿态进行安全性判定。降落平面检测装置如图3所示。

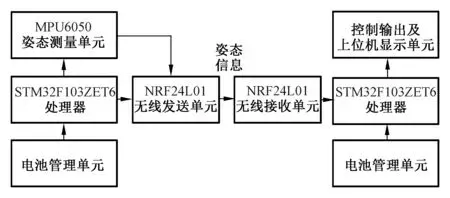
图2 降落平面检测系统图Fig. 2 Landing plane detection system

图3 降落平面检测装置Fig. 3 Landing plane detection device

1.2 降落标志

无人机降落时，主要依靠机载摄像头捕捉无人艇甲板上的降落标识，因此一个特征突出并容易识别的降落标志尤为重要。在本文中，设计的专用降落标志如图4所示。标志主体由一个圆环和一个内接正三角形构成。此三角形分为两部分，由顶点向下作垂线，左侧为白色右侧为黑色，中间的垂线便于无人机与无人艇之间朝向校准。

图4 降落标志Fig. 4 Landing sign

1.3 捕获图像的预处理

运动中的无人机在通过机载摄像头捕获图像时，会受到诸如光子噪声和暗电流噪声等因素的干扰，导致图像中噪声信息的引入，因此需要在尽量保持图像细节特征的前提下，对图像的噪点进行抑制即图像滤波[11]。常用的图像滤波方式有线性滤波和非线性滤波，但对于图像中存在有效像素值为0噪声像素值为255的情况下，线性滤波只能将噪声处理为更柔和的形式，而非线性滤波可以通过逻辑判断将该噪声过滤掉[12]。

非线性滤波中常用的滤波方式包括中值滤波和双边滤波，二者相比较，中值滤波会使图像的边缘信息变弱甚至消失，而为了对所设计的降落标志进行识别，需要对图像的边缘进行精准的把握，因此本文选择了不仅能将图像中所带有的噪声滤除掉，同时也不会变动图像中有效信息的双边滤波算法。双边滤波可以使频率较高的信号变得平滑，还会使变化较大的信号维持原样，实现对边缘的平滑处理。双边滤波器表达式为

式中，g(i,j)为被卷积的像素点(i,j)的像素强度，f(k,l)为邻域像素点(k,l)的像素强度，ω(i,j,k,l)为加权系数，其等于值域滤波器d(i，j，k，l)与空域滤波器r(i，j，k，l)的乘积。空域滤波器与值域滤波器的表达式分别为

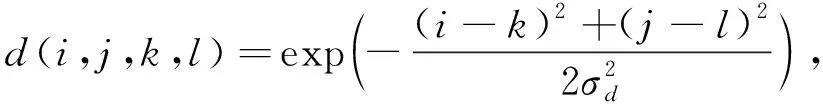
式中，σd与σr为平滑参数，f(i,j)与f(k,l)分别为邻域像素点(i，j)和(k，l)的像素强度。

采用上述方法对降落标志图像进行预处理得到的轮廓清晰的二值化图像如图5(b)所示。

图5 捕获的图像与二值化后的图像Fig. 5 Captured image and binarized image

仿真研究和实际测试效果表明：采用双边滤波法进行图像预处理时，主要涉及的参数包括每个像素邻域的直径、颜色空间滤波器的标准差值和空间坐标滤波器的标准差值。综合考虑运行速率与处理效果，滤波器的具体参数选择见表1。

表1 双边滤波参数Tab.1 Bilateral filtering parameters

1.4 捕获阶段1——圆环检测

OpenCV提供了圆形检测算法，最常使用的是霍夫变换[13-14]，通过在两个空间坐标系间对像素进行变换，可以令在初始空间坐标系包含同样性质的曲线变换到另一个空间坐标系中并且数值增大到峰值，如此便可以将检测边缘形状问题转变成峰值捕获过程。在检测圆形过程中，将图像空间xy直角坐标系中的像素映射到参数空间中，并在参数空间中搜索交点是否存在，圆形的数学表达式为

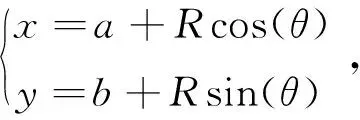
式中，(a,b)为圆心坐标，θ为半径与x轴的夹角。在OpenCV中提供了HoughCircles函数用来检测灰度图像中是否包含有圆形，在此需要合理设置两圆心距离的最小值。若最小值太小，除了捕获到需要的圆形外还会检测到其余临近的圆形，给图像识别带来干扰；若最小值太大，则有可能会对图像处理不完全，有所漏失，经过仿真和实验研究，本文选取的各参数取值见表2。

表2 HoughCircles函数参数Tab.2 HoughCircles function parameters

对原图像进行圆形捕获，并将捕获结果显示在原图像上，如图6(b)所示。

图6 原图像与圆形捕获Fig. 6 Original image and circular capture

1.5 捕获阶段2——三角形检测

当无人机降落至距无人艇甲板50 cm左右时，由于高度过低，会存在无法完全捕获圆环的可能，因此转为对内部小三角形的识别，并通过三角形内部的垂线，来判断无人艇的朝向，使无人机与无人艇进行朝向校准。对三角形捕获仿真如图7(b)所示。

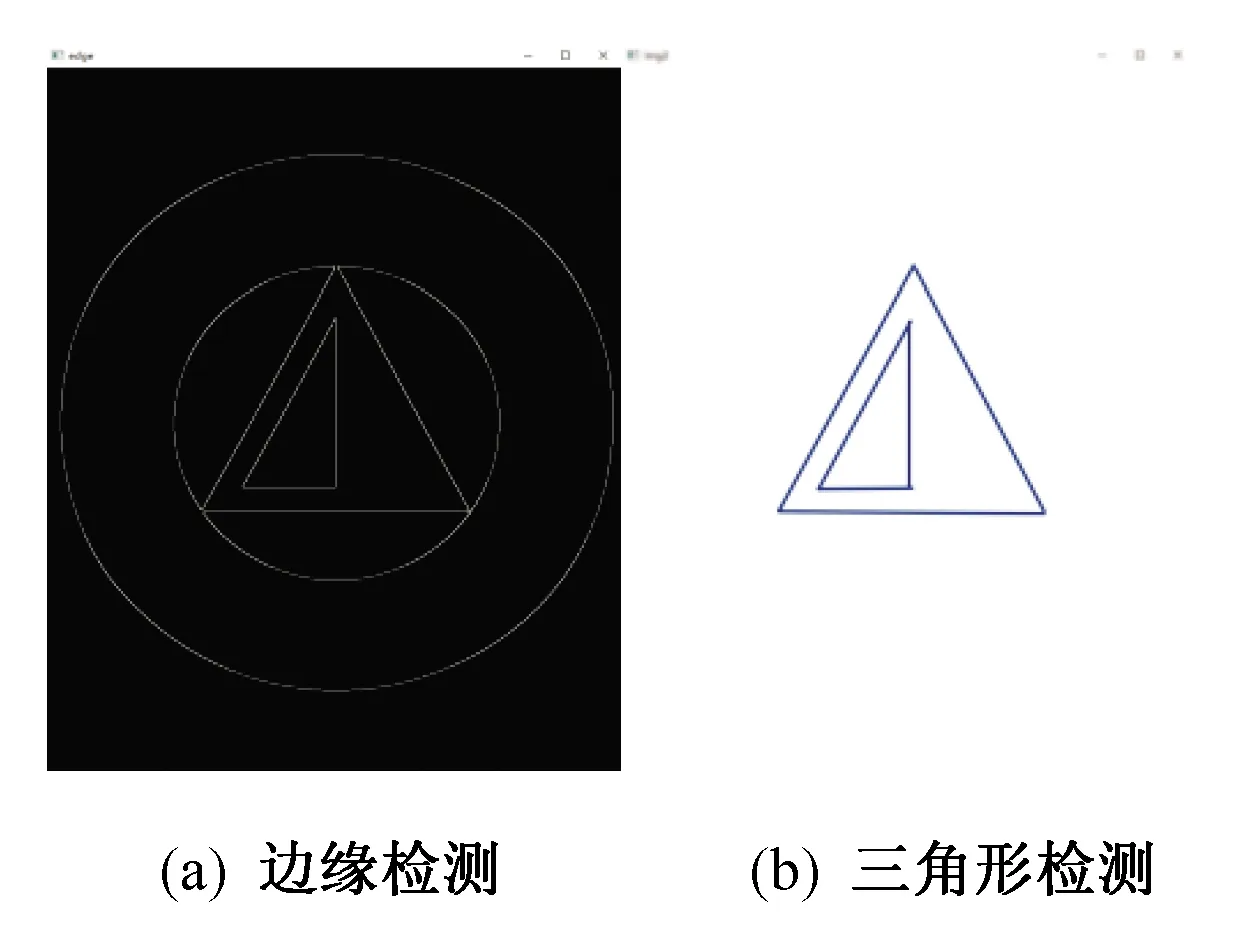
图7 边缘检测与三角形捕获Fig. 7 Edge detection and triangle capture

1.6 坐标空间的转换

在无人机自主降落的整个系统中，涉及4种不同坐标空间的转换，分别是世界坐标系、机体坐标系(相机坐标系)、图像坐标系和像素坐标系。世界坐标系OwXwYwZw以目标物体为原点，建立规则符合右手坐标系，通过世界坐标系对无人机位置进行定位。由于机载摄像头固定在无人机中心处，可以将机体坐标系与相机坐标系看作是同一个坐标空间。相机坐标系的原点Oc为相机镜头的光心，OcZc轴与相机的光轴重合，OcXc轴平行成像平面并指向右侧，OcYc轴垂直OcXcZc屏幕并指向下方。像素坐标系OpXpYp主要是用来定义相机所捕获图像中每个像素位置之间的关系，它的原点为图像左上方的顶点，OpXp轴和OpYp轴分别与图像坐标系中OiXi轴和OiYi轴方向一致。与像素坐标系相对应的图像坐标系主要是用来定义图像的真实长度，光轴在感光片上对应点为原点Oi，OiXi平行向右，OiYi与OiXi垂直并指向下方。图像坐标系与像素坐标系具体如图8所示。

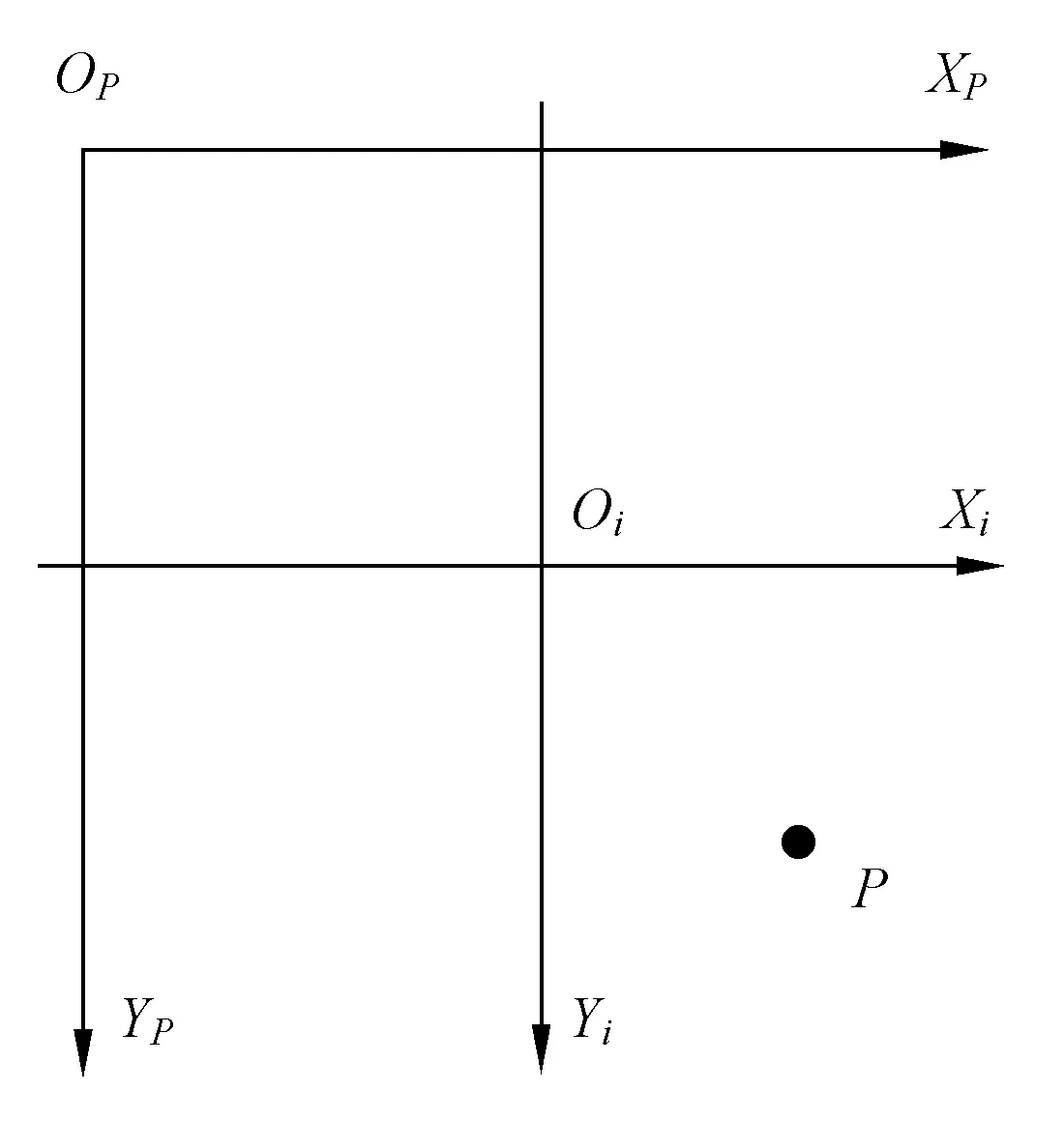
图8 图像坐标系与像素坐标系Fig. 8 Image coordinate system and pixel coordinate system

图片中的点P，在图像坐标系中坐标为P(xi,yi)，在像素坐标系中坐标为P(xp,yp)，两者之间的关系为

(1)

式中，xi0和yi0为图像坐标系原点在像素坐标系中的位置，通常取值为图像长度的一半，dxp与dyp分别表示一个像素的物理宽度和高度。

空间中一三维点P(xc,yc,zc)在图像坐标空间中投影点为P′(x′,y′)如图9所示，为便于分析计算，作图像平面关于光心的对称平面，三维点在此平面投影点为P(x,y)，如此便可以得到三维空间的点与图像中的点之间的转换关系为

图9 点到图像坐标系的映射Fig. 9 Mapping of points to image coordinate systems

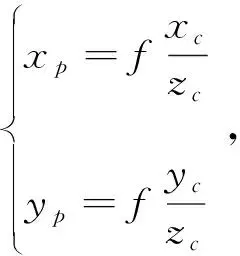
(2)

式中，f为焦距，即图像平面到光心的距离。将式(2)代入式(1)并转化为矩阵形式可以得到

式中，K为摄像头的内参矩阵，通过内参矩阵可以将相机坐标系下任意的三维坐标映射到像素坐标系中，构建空间点与像素点之间的映射关系。

2 四旋翼飞行器数学模型

依据四旋翼飞行器飞行控制的特点，建立了姿态与位置的数学模型，并利用Simulink工具对四旋翼飞行器模型进行模拟，在建模过程中所需要的四旋翼飞行器的参数见表3。

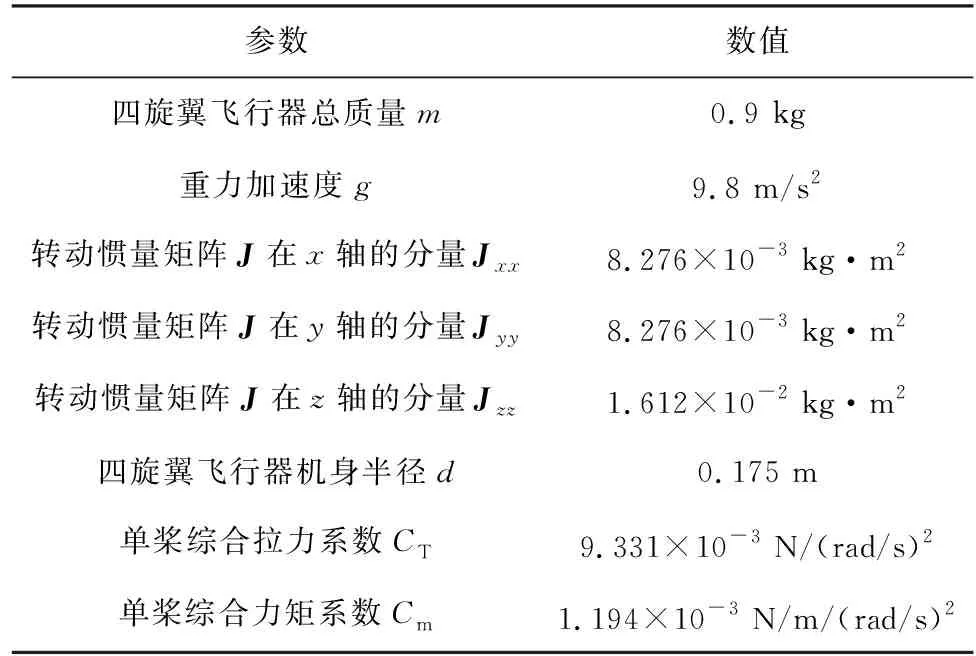
表3 四旋翼飞行器参数表Tab.3 Quadcopter parameter

2.1 姿态模型

以“十”字形四旋翼飞行器为例，为不失一般性，假设四旋翼飞行器为均匀对称的刚体[15]，如图10所示。

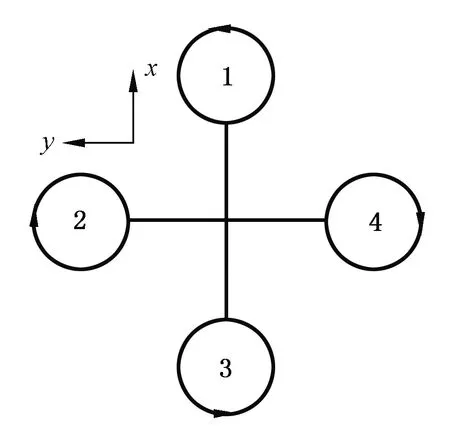
图10 十字形四旋翼飞行器Fig. 10 Cross-shaped quadcopter

对其进行动力学分析，已知力矩计算公式为

M=L×F,

式中,L是转动轴到受力点的距离，F是作用于物体上的矢量力。对于x轴来说，力矩由电机2与电机4产生，电机2产生正向力矩，电机4产生负向力矩，同理对于y轴来说，力矩由电机1与电机3产生，电机3产生正向力矩，电机1产生负向力矩。根据x轴与y轴的方向可知，z轴垂直纸面向上，因此对于z轴，电机2与电机4产生正向力矩，电机1与电机3产生负向力矩。可得到各轴上的力矩为

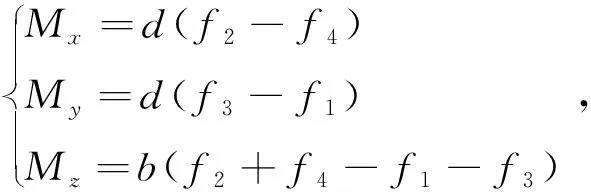
(3)

式中，d为无人机中心到旋翼的距离，b为系数，f1、f2、f3、f4分别为四个电机产生的力，其力的大小为

式中，CT为升力系数，ωi为电机转速,i=1,2,3,4。由式(3)可以得到四旋翼飞行器的合力矩为

M=Jε+w×Jw

(4)

式中，J为惯量矩阵，ε为角加速度，w为角速度，具体表达式为

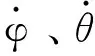
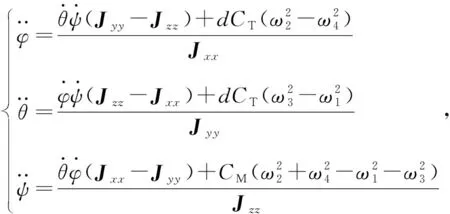
(5)

由此即可建立出角加速度与角速度和电机速度的数学模型。

2.2 位移模型

在位移模型建立过程中，需要涉及两个坐标系，分别是地面坐标系和机体坐标系，机体坐标系转为地面坐标系的转换矩阵为Rbg，

每个电机在机体坐标系下都会产生一个向上的升力fi，同时四旋翼飞行器也会受到自身垂直向下的重力的作用，受到的合力为

式中,ax、ay和az分别为四旋翼飞行器在各坐标轴上的加速度，将之转换到地面坐标系

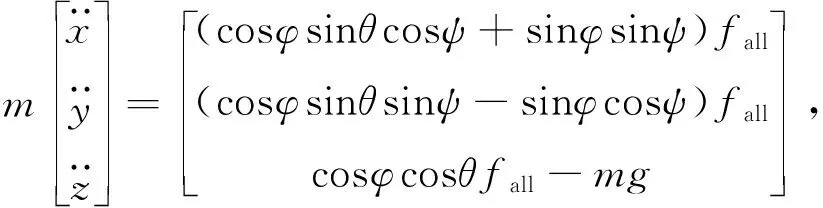
(4)

式中，fall=f1+f2+f3+f4。

2.3 控制模型

在四旋翼飞行器的控制系统中，采用PD控制，外环为位置控制，对式(5)进行变换，可得

式中，Ux、Uy和Uz分别为x、y和z轴的虚拟控制量。四旋翼飞行器的内环为姿态控制，由式(5)可知，φ受到电机2与电机4的影响，θ受到电机3与电机1的影响，可以得到电机转速与控制量之间的关系式

式中，U1为位置控制量，U2、U3和U4为姿态控制量，通过转换矩阵将控制量转换为电机转速，实现对四旋翼飞行器的控制。

2.4 仿真结果

本次Simulink仿真设计了4个任务目标点，四旋翼无人机由原点(0,0,0)起飞，依次飞向目标点(0,0,5)，(5,0,5)，(5,5,5)，(0,5,5)，最后垂直降落，仿真结果如图11所示。可以看出此模型可以有效帮助四旋翼飞行器追踪目标地点。

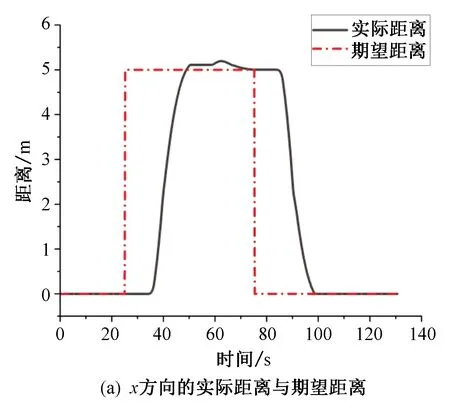
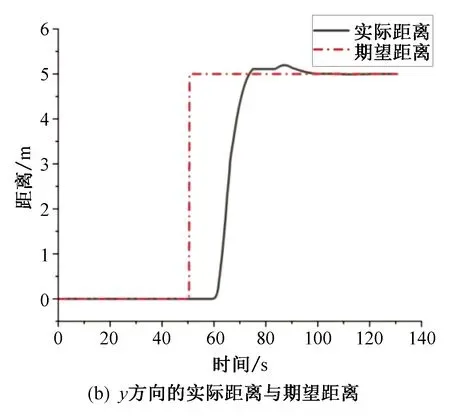
图11 实际距离与期望距离Fig. 11 Actual distance and expected distance

3 降落测试实验

四旋翼飞行器能否平稳降落在无人艇甲板上，主要需要考虑的因素包括两点，分别是四旋翼飞行器与甲板之间的摩擦力以及甲板的倾角。而甲板的倾角包括俯仰角θ与滚转角Φ，四旋翼飞行器分别在降落平面俯仰角θ与滚转角Φ的作用下产生沿斜面向下的分力为

Fθ=mgsinθ,

FΦ=mgsinΦ,

结合两个分力，可以得到无人机沿斜面向下的合力为

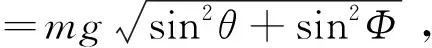
(6)

四旋翼飞行器与降落平面之间的最大摩擦力为

fmax=mgμsinα,

(7)

式中,μ为摩擦力系数，α为降落平面与水平面之间夹角的极限值。根据式(6)和(7)，使四旋翼飞行器能够安全着陆，沿斜面向下的合力要小于最大静摩擦力，因此降落平面的俯仰角θ与滚转角Φ要满足

sin2θ+sin2Φ≤μ2sin2α,

为确定最大静摩擦力即确定四旋翼飞行与降落平面间最大夹角，进行了十次实验如图12所示，确定在本文所设计的系统方案中安全降落的倾角阈值，具体实验数据见表4。

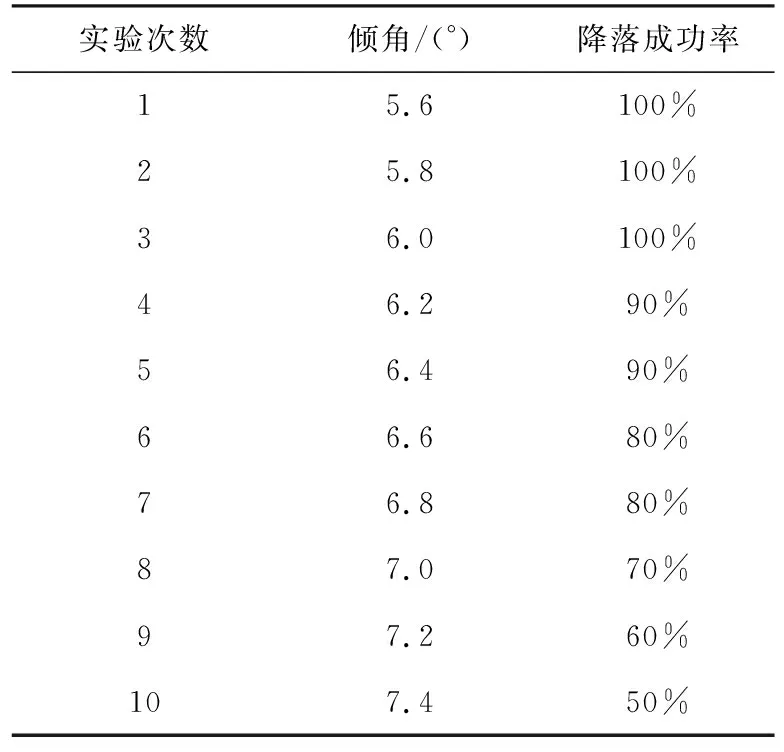
表4 降落平台倾角测试Tab.4 Landing platform inclination test

无人机降落倾角测试实验如图12所示。当降落平面与水平面夹角处于6°之间时 ，无人机可以安全着陆于目标甲板上，超过此角度则不能确保无人机着陆的安全性与稳定性。

图12 平台倾角测试实验Fig. 12 Platform inclination test experiment

根据上述对降落平面俯仰角与横滚角的综合分析，设计了降落平面倾角监测上位机，可以实时监测倾角状态并进行降落判定，如图13所示。

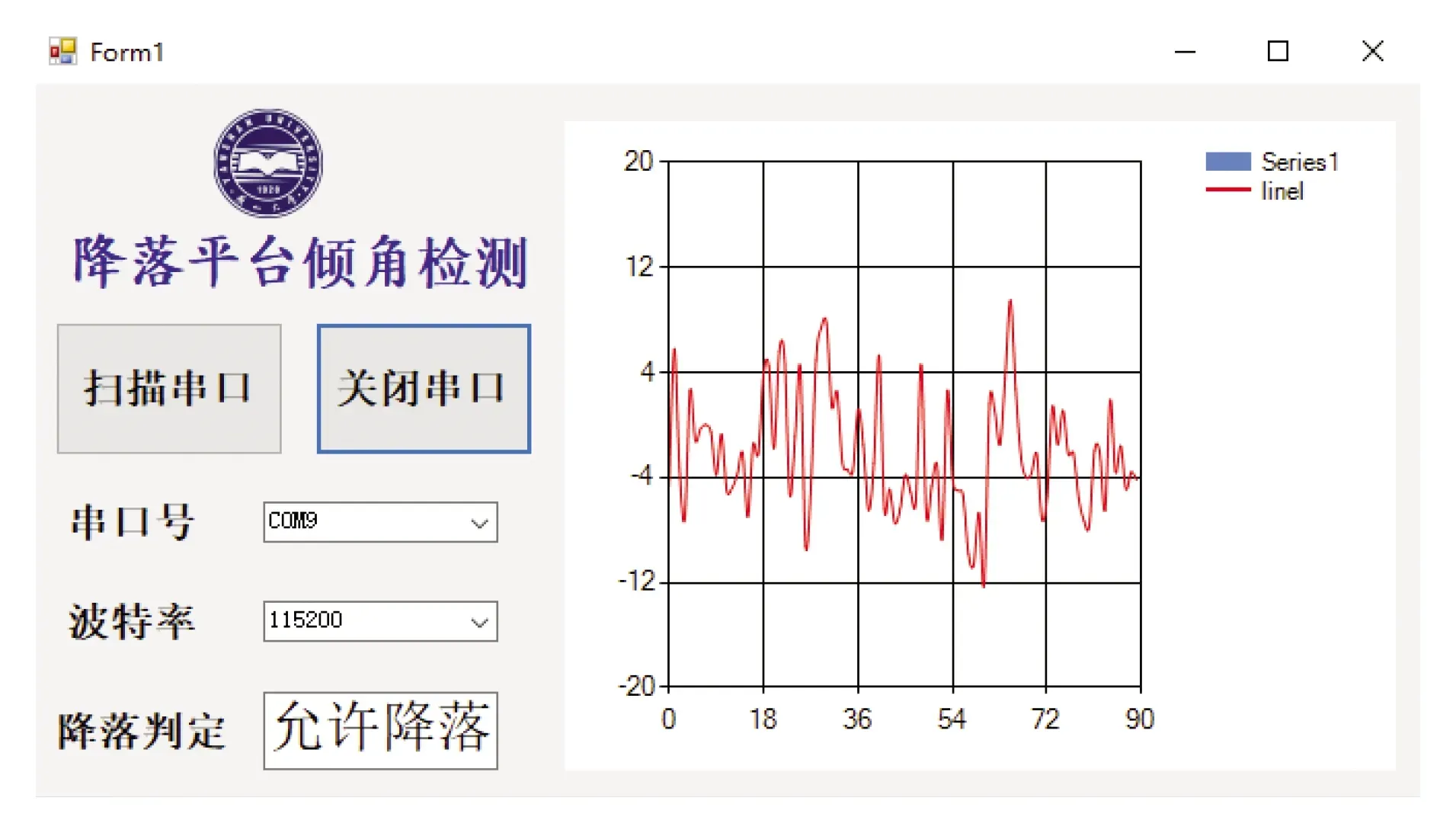
图13 无人艇上降落平面的监测Fig. 13 Monitoring of landing planes on USV

分别对是否使用降落平面检测系统进行了十次降落实验，在实验过程中，通过人为随机晃动降落平面来模拟无人艇在海面上的起伏状态，如图14所示。未使用降落平面检测系统的情况下，无人机不考虑降落平面的状态而持续降落，在十次实验中有四次会因平面倾角过大而滑落,降落成功率为60%。在使用降落平面检测系统后，无人机在将降落平面倾角过大的情况下，保持悬停状态，在安全倾角范围内进行降落，十次实验中仅有一次降落失败,降落成功率为90%。实验表明：采用文中方法能够将降落的成功率提高30%，无人机在动态平面上的降落安全性得到了提升。

图14 降落效果检测实验Fig. 14 Landing effect test

4 结论

本论文在总结国内外无人机控制与视觉识别技术的基础上，结合动态降落平面的姿态变化，针对海面无人艇起伏状态下无人机自主着舰问题，提出了一种基于降落平面姿态主动反馈的无人机降落方案。在模拟无人艇状态下进行无人机自主降落实验，结果表明，在以降落平面与水平夹角为6°的条件下，采用此方案进行降落的成功率提升了约30%，因此本方案适用于海上无人艇等动态平面环境下的无人机着陆。