一种高效的概率-证据混合工业机器人定位精度可靠性分析方法
2022-08-01梁云飞张德权彭周源
梁云飞,张德权,彭周源
(河北工业大学 机械工程学院,天津 300401)
0 引言
工业机器人广泛应用于搬运、焊接、喷漆和装配等工业制造领域,其定位精度是工业界和学术界共同关心的问题。影响工业机器人定位精度的不确定因素主要包括制造误差[1],核心零部件磨损[2],控制信号迟滞和复杂作业环境[3]等。上述不确定因素可以分为随机不确定性和认知不确定性。随机不确定性一般源于加工设备的误差、材料不均匀性、环境随机性等,可采用概率模型对其进行描述。认知不确定性往往源于某种程度上知识的不完备,对于一个复杂的结构系统,通常无法收集足够的信息建立精确概率模型来评估其可靠性,可采用证据理论[4-5]对其进行描述。
在研究随机不确定性与认知不确定性混合问题方面,近年来公开报道了一些研究成果。Du[6]运用概率模型和证据理论提出了随机不确定性和认知不确定性混合的可靠性分析框架。姜潮等[7]针对同时包含概率变量和证据变量的混合不确定问题,提出了一种高效的结构可靠性分析方法。Xiao等[8]在基于证据理论的可靠性分析中引入支持向量回归模型显著提高计算效率。
近年来学者们已在工业机器人运动精度可靠性分析的研究方面开始进行探索。许昌瑀等[9]基于运动学模型分析了关节间隙对工业机器人单点定位精度可靠性的影响。Rao和Bhatti[10]提出工业机器人运动学和动力学的概率建模方法,并研究不确定参数对末端执行器定位精度的影响。Kim等[11]考虑连杆长度和关节间隙研究工业机器定位精度的可靠性。Pandey和Zhang[12]采用最大熵原理获得机器人位置误差的极值分布及其概率密度函数,并对机器人进行运动精度可靠性分析。Zhang和Han[13]考虑工业机器人连杆长度和关节转角为正态分布不确定变量,采用单变量降维积分法计算工业机器人单坐标方向定位误差的统计矩,并基于鞍点近似法分析工业机器人的单点定位精度可靠性。然而,对工业机器人系统内随机不确定性和认知不确定性混问题合的研究,目前仍鲜见报道。限制此类研究发展的主要原因是其中涉及多层嵌套优化,较低的计算效率限制了在实际工程问题中的应用。
为解决工业机器人系统中存在的一类随机不确定性和认知不确定性可靠性分析效率低的问题,本文引入Kriging代理模型代替复杂的工业机器人运动学模型进行定位精度可靠性分析。在此基础上提出一种高效的概率-证据混合定位精度可靠性分析方法,能够大幅度提高可靠性分析效率,通过工业机器人实例验证了所提方法的工程实用性。
1 工业机器人运动学模型
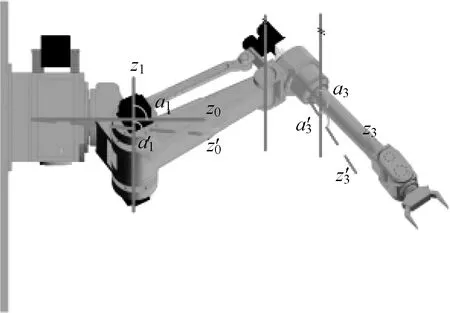
工业机器人运动学模型描述了本体结构参数与末端运动响应之间的函数关系,根据该函数关系可对工业机器人的定位精度进行可靠性分析。工业机器人可看作是由一系列连杆通过关节连接构成的,若各个关节的参数已知,便可从基座固定坐标系通过连杆坐标系的传递,推导出末端执行器的位姿坐标。工业机器人D-H运动参数示意图如图1所示。
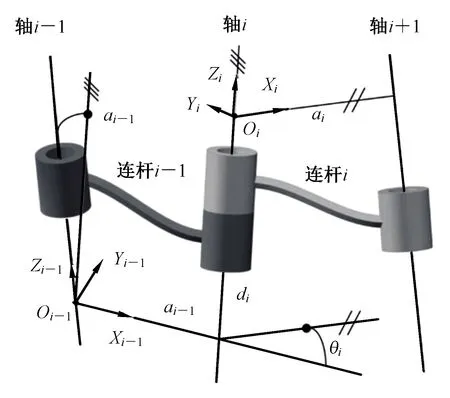
图1 工业机器人D-H运动参数Fig.1 D-H kinematic parameters of industrial robots
在图1中,ai表示第i个连杆沿xi方向的长度,αi表示第i个连杆两关节轴线之间的扭角,θi表示两连杆之间的夹角,di表示沿关节i轴线两个公垂线的距离。连杆坐标系的旋转和平移变换可通过这4个参数描述,每个关节连杆坐标系的建立规则如下:
1) 坐标轴x指向旋转轴i-1和i的公法线方向,从关节i-1指向关节i;
2) 坐标轴z与关节轴线重合;
3) 坐标轴y按照右手螺旋法则确定。
建立好各个连杆坐标系之后,便可通过连杆坐标系的平移和旋转变换实现相邻连杆坐标系之间的转换。连杆坐标系沿坐标轴的平移变换矩阵T(·)表示为
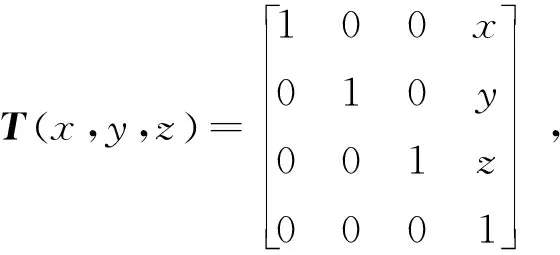
(1)
式中,x、y和z分别表示沿x轴、y轴和z轴移动的距离。
坐标系绕三个坐标轴的旋转变换矩阵R(·)分别表示为

(2)

(3)
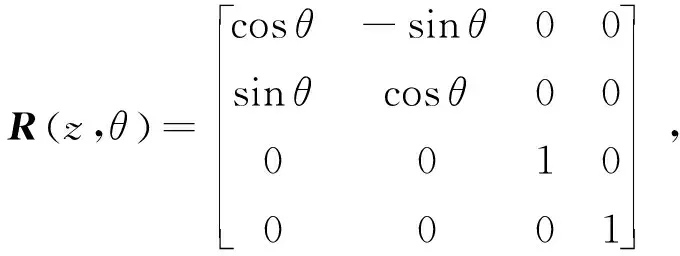
(4)
式中,R(x,θ)表示绕着x轴旋转θ角度,R(y,θ)和R(z,θ)同理。
以坐标系Oi-1变换到坐标系Oi为例,过程如下:
1) 坐标系Oi-1绕zi-1轴旋转θ角度,旋转变换矩阵为R(z,θ);
2) 坐标系Oi-1沿zi-1轴平移l距离,平移变换矩阵为T(0,0,l);
3) 坐标系Oi-1绕xi轴旋转α角度,旋转变换矩阵为R(x,α)。
则总的变换矩阵Ai可表示为
Ai=R(z,θ)·T(0,0,l)·R(x,α)。(5)
对于本文所研究的六自由度工业机器人,依次右乘变换矩阵Ai可得到机器人末端坐标系相对于固定参考坐标系的位姿矩阵T6:
T6=A1·A2·A3·A4·A5·A6=
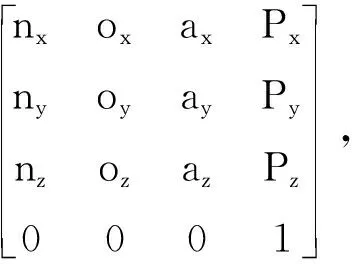
(6)
式中,矩阵的前3列表示工业机器人末端的姿态,第4列表示末端中心点的位置。本文将末端中心点设为目标点,分析工业机器人末端的定位精度可靠性。
2 证据理论基本概念
证据理论[14]可有效地描述工业机器人认知不确定参数,采用可信度(Belief measure,Bel)和似真度(Plausibility measure,Pl)组成的区间来量化工业机器人不确定性。证据理论的一些基本概念如下:
识别框架(Frame of Discernment,FD)是所有相互独立的基本命题的集合,通常用Θ表示。假设识别框架为Θ={s1,s2},其中s1和s2表示相互独立的基本命题或集合,则识别框架内所有基本元素可以构成幂集2Θ={∅,{s1},{s2},{s1,s2}},每一个命题对应幂集中的一个子集。
基本可信度分配(Basic Probability Assignments, BPA)为确定识别框架后,根据信息进行可信度分配,即描述命题的可信程度。若函数m:2Θ→[0,1]为Θ的幂集,且满足以下性质:
m(D)≥0,∀D∈2Θ,
(7)
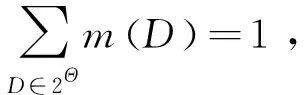
(8)
m(∅)=0,
(9)
则称m为识别框架Θ上的基本可信度分配,其中m(D)>0的集合D叫做焦元。
当识别框架Θ中有多个证据变量S1,S2,…,Sn,且变量之间相互独立,其联合BPA可表示为
mS(Sk)=
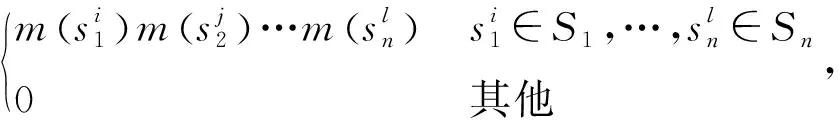
(10)

采用Bel和Pl构成的区间测度来描述命题的信任程度,可表示为
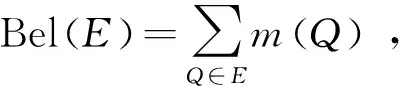
(11)
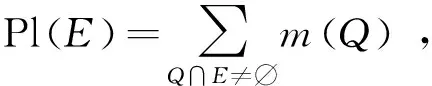
(12)
Bel(E)表示所有包含在命题E内的焦元BPA之和,可认为是对命题E一定成立的信任程度;Pl(E)表示所有与命题E有交集的焦元BPA之和,可认为是对命题E可能成立的信任程度。本文中,Bel和Pl分别表示工业机器人定位精度可靠度的区间下界和上界。
3 常规的分析方法
针对工业机器人系统中存在的一类随机不确定性和认知不确定性混合的情况,将工业机器人连杆长度和关节转角此类容易测得参数信息的变量考虑为概率变量;将连杆扭角等难以准确获得参数信息的变量考虑为证据变量。定义输入变量为I=(X,Y),假设所有输入变量之间相互独立,其中X=[X1,X2,…,XnX]T表示随机不确定变量,nX为随机不确定变量的维数,用概率模型描述;Y=[Y1,Y2,…,YnY]T表示认知不确定性变量,nY表示认识不确定性变量的维数,用证据理论描述。在证据变量的联合空间Y中,用CYi(i=1,2,…,n)表示各焦元,其中n表示焦元个数。定义工业机器人x、y和z三个方向定位精度的功能函数分别为
gx(X,Y)=|Qx-Px|,
(13)
gy(X,Y)=|Qy-Py|,
(14)
gz(X,Y)=|Qz-Pz|,
(15)
式中,Q(Qx,Qy,Qz)是将所有不确定输入变量代入工业机器人运动学方程得到的末端执行器相对基坐标系在空间中的坐标点,P(Px,Py,Pz)为工业机器人末端执行器的名义目标点。
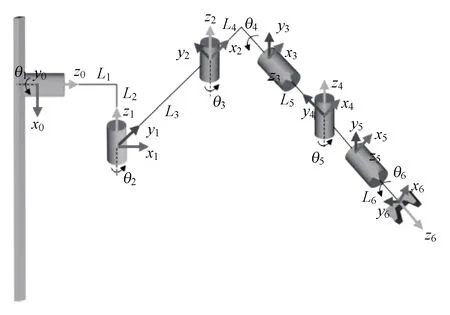
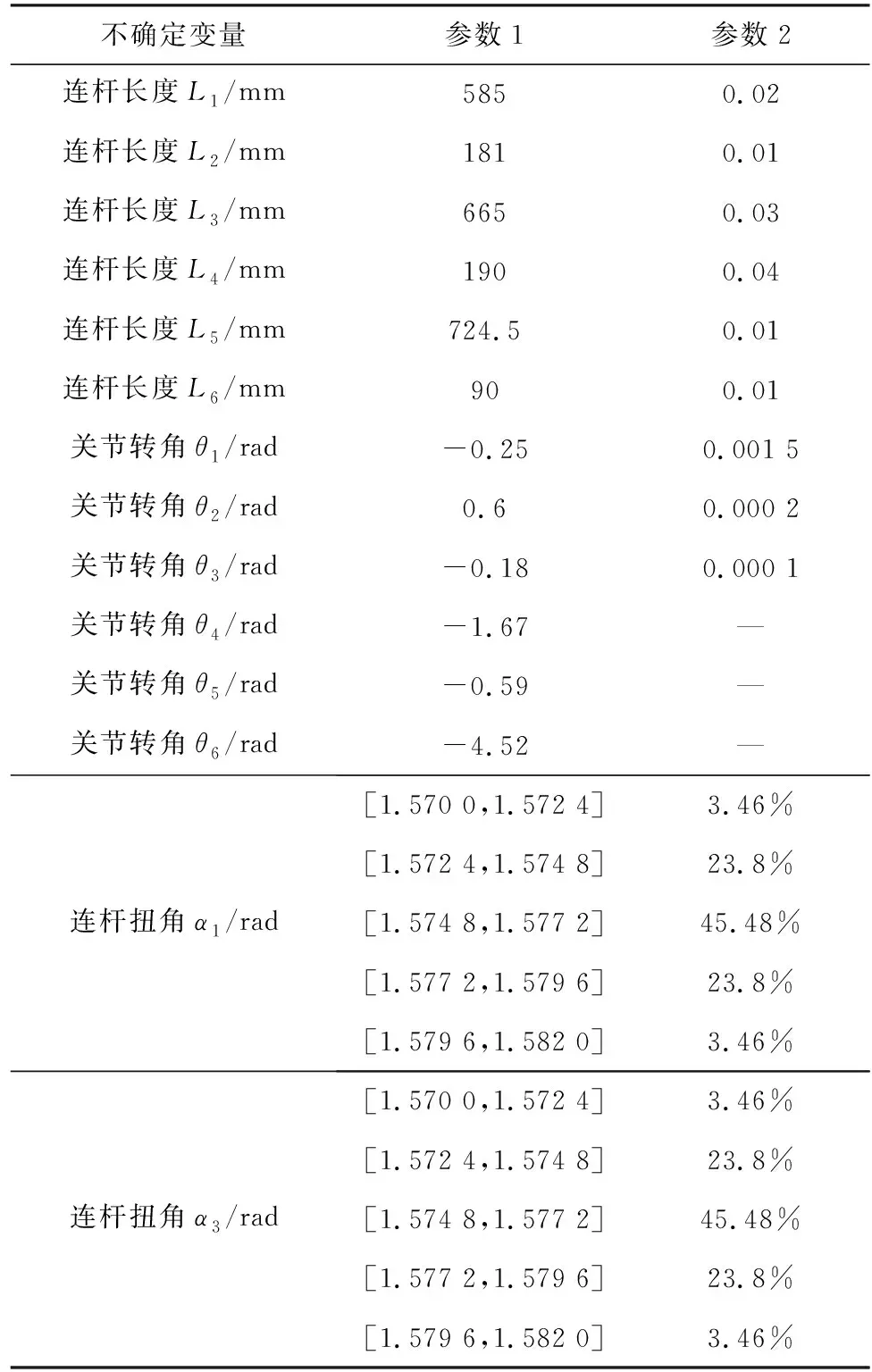
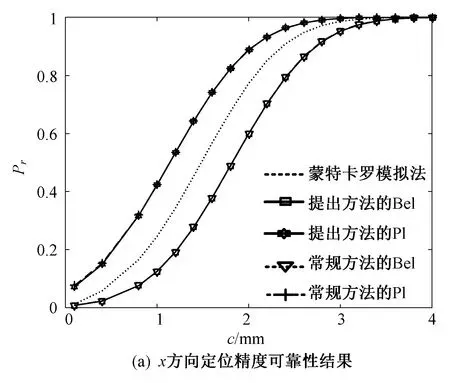
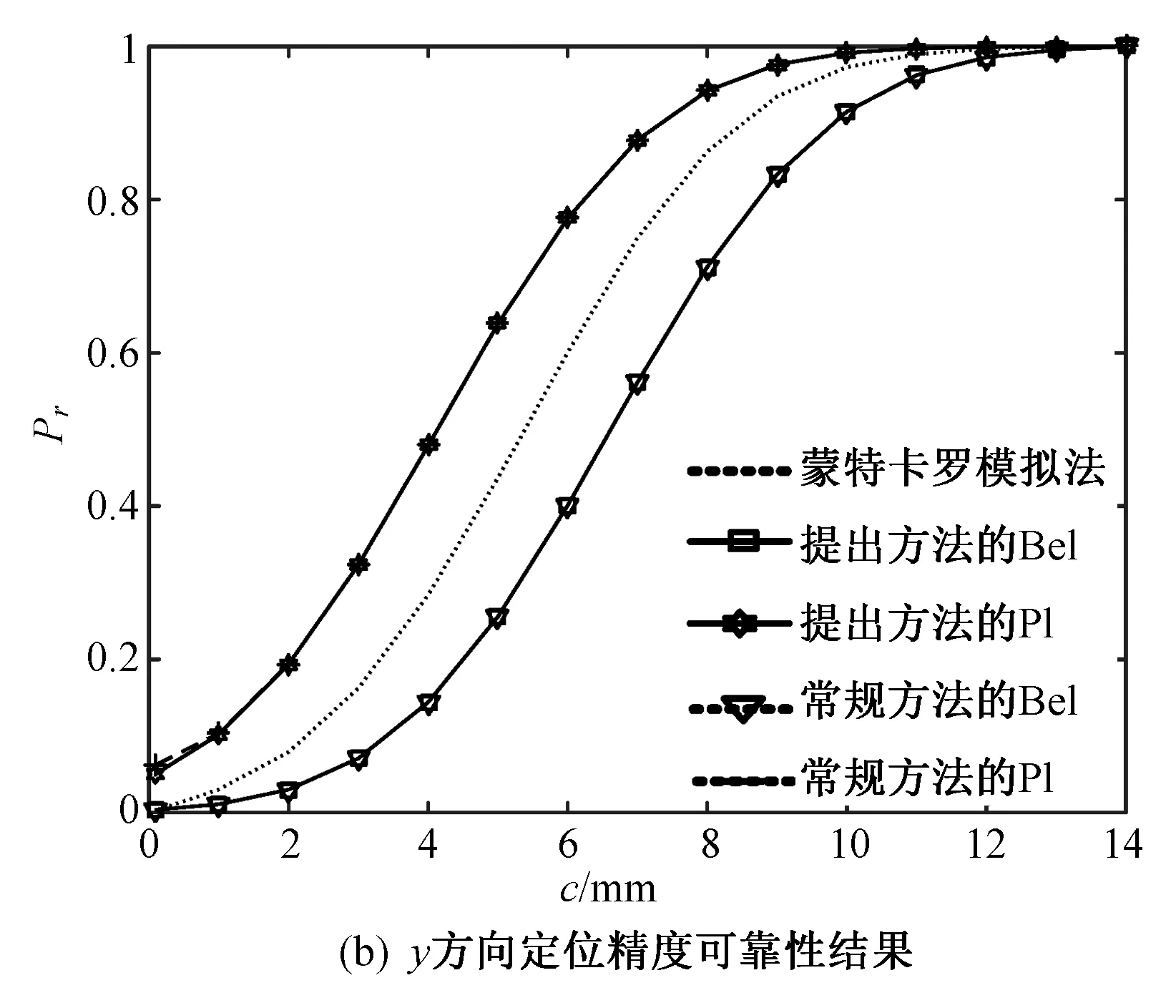
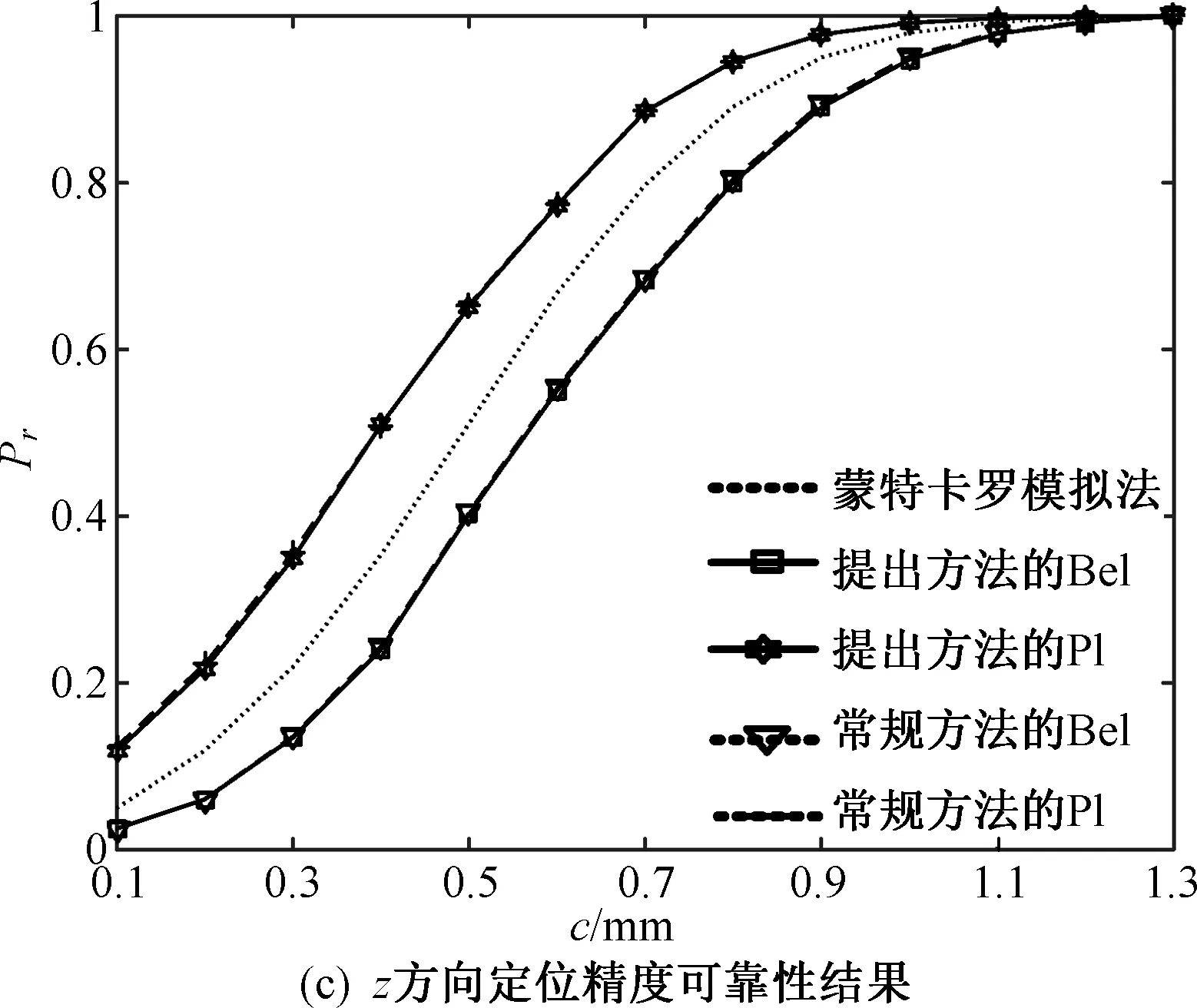
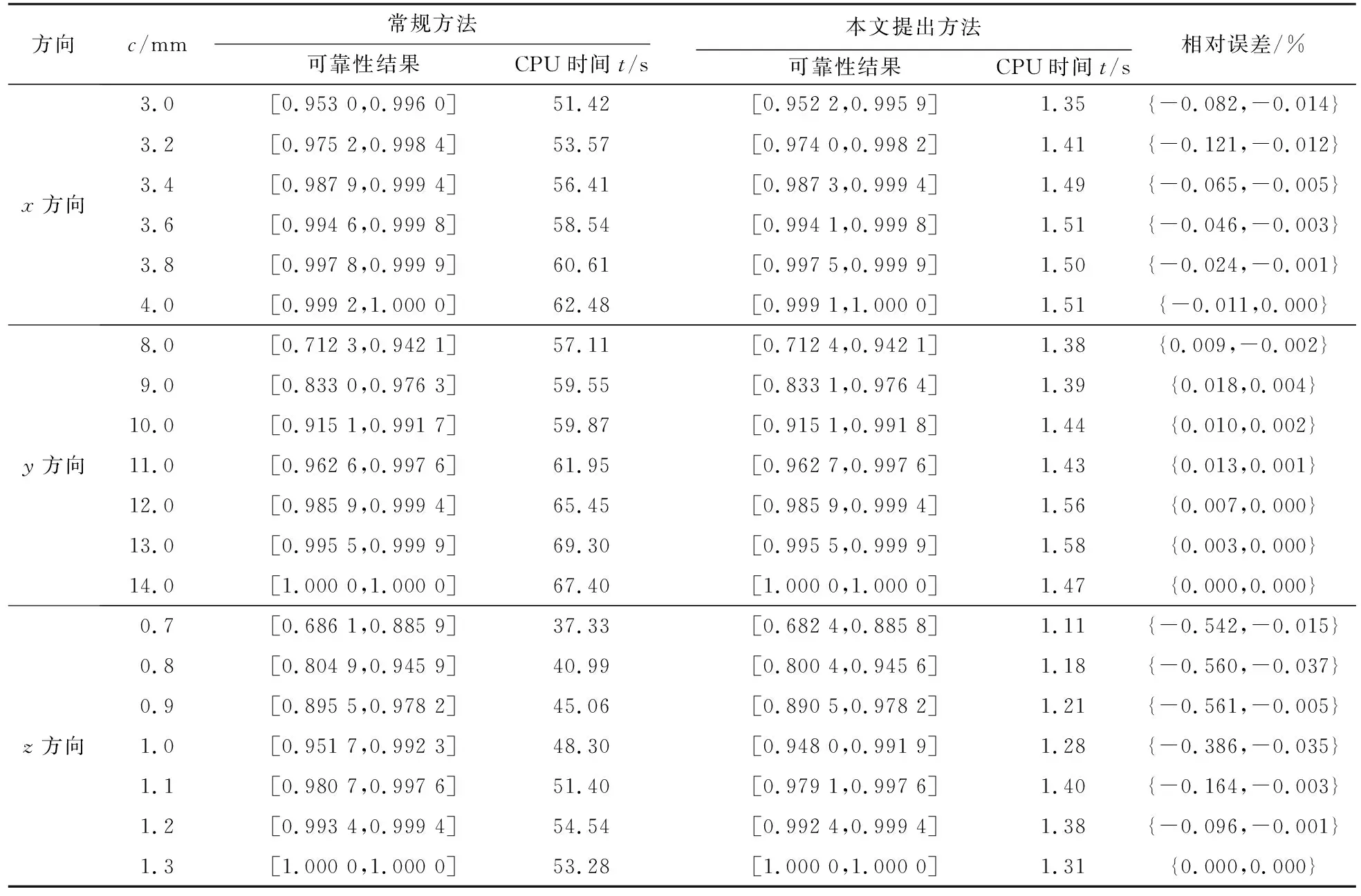
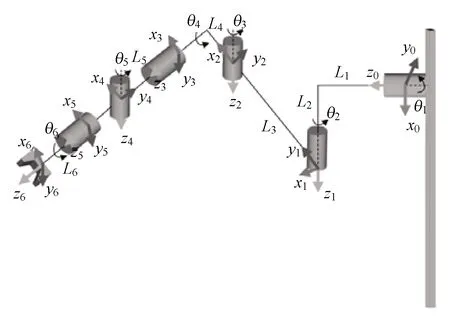
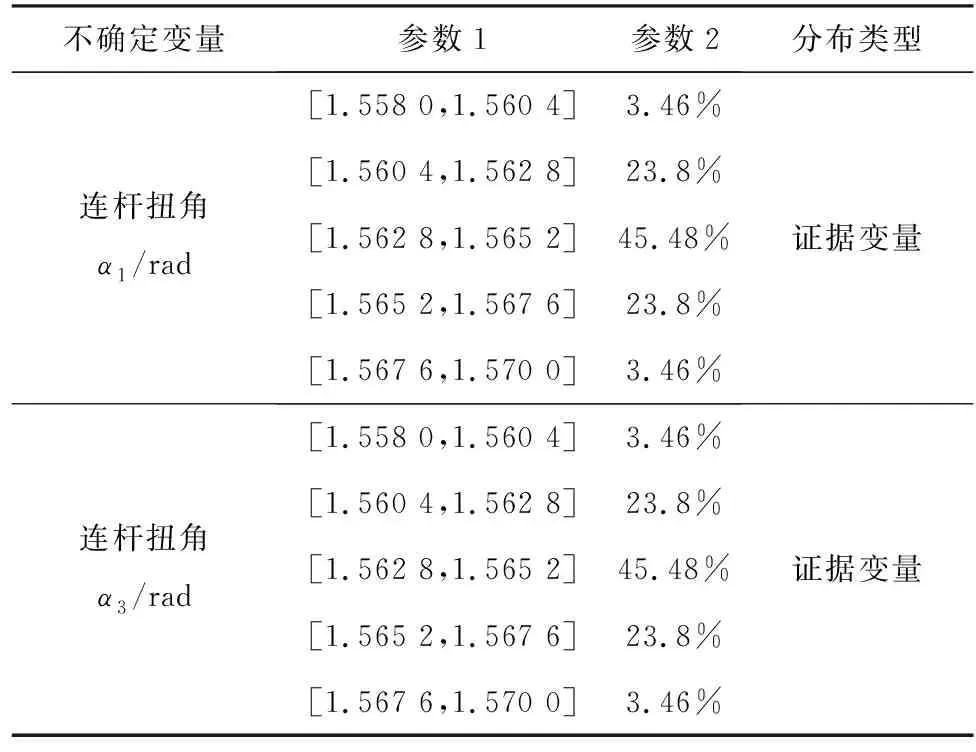
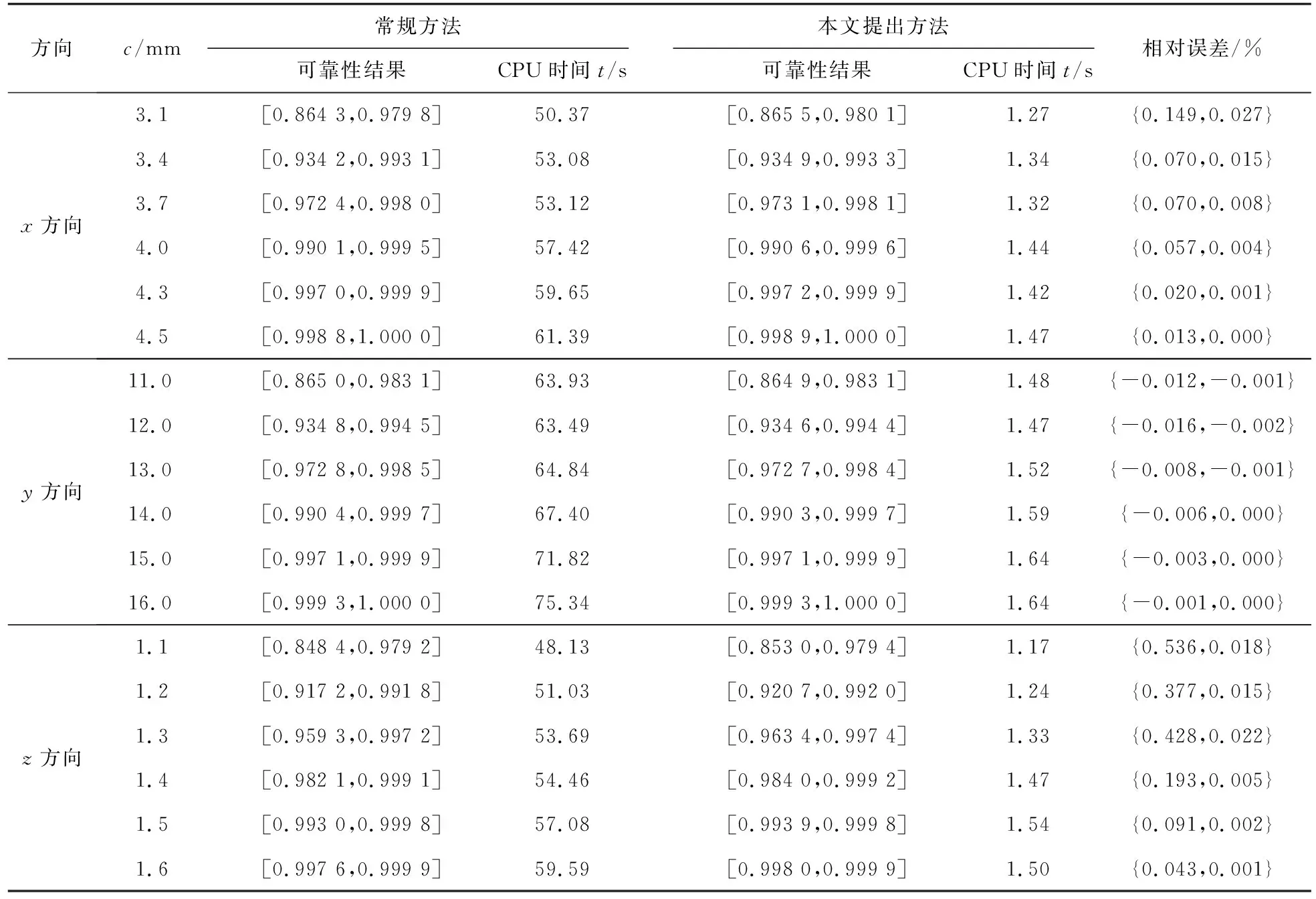
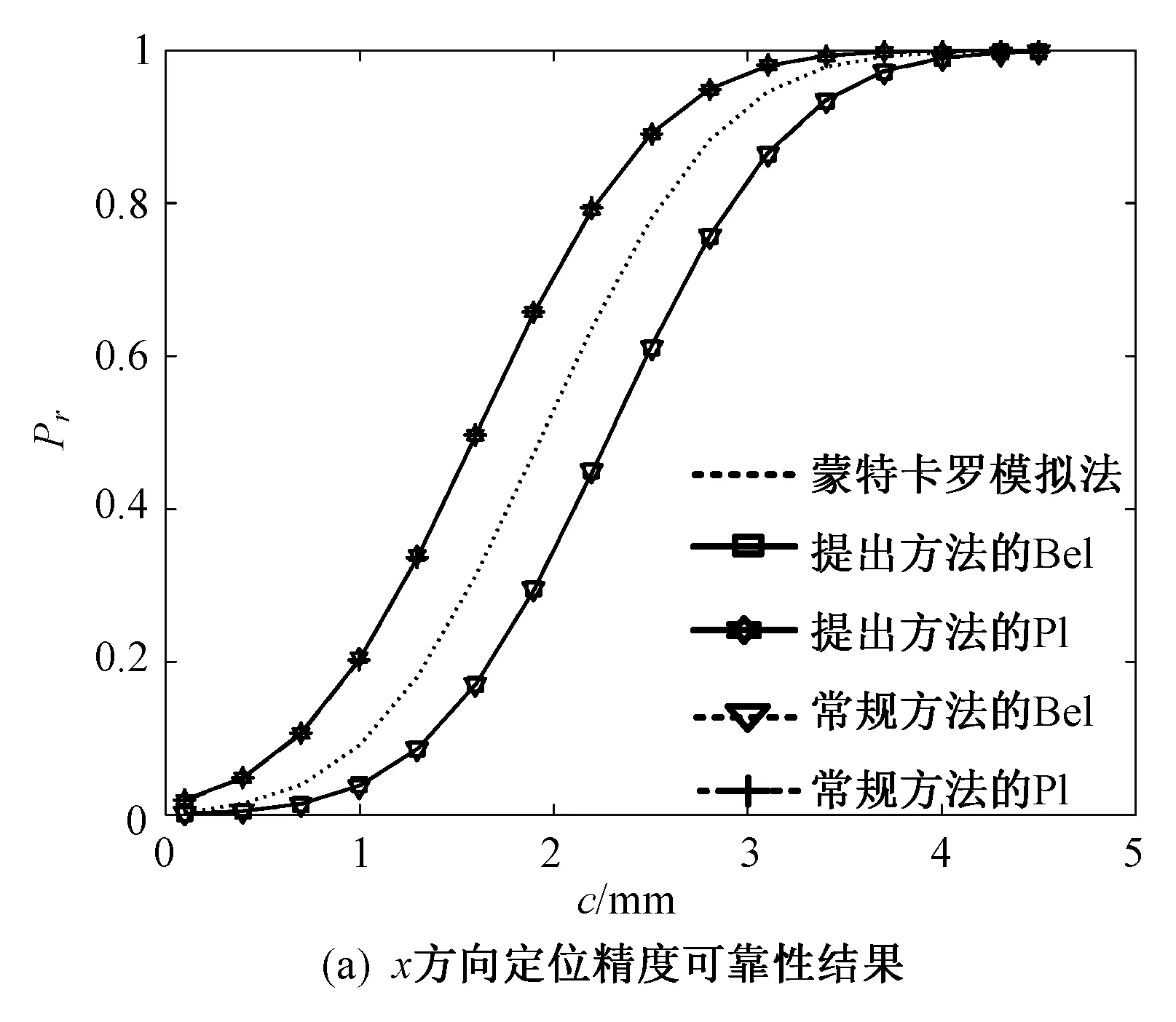
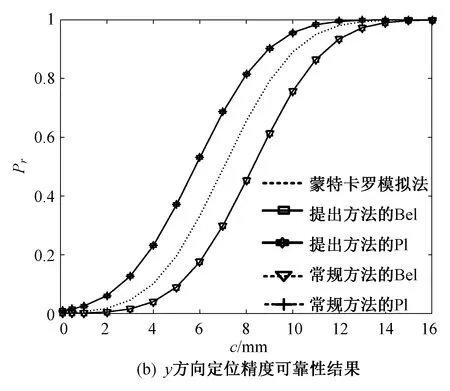
以x方向的定位精度可靠性分析为例,如图2所示,由于证据变量和随机变量同时存在,输入空间被划分为n个子空间CXYi=(X,CYi),i=1,2,…,n,gx(X,Y) 图2 不确定变量输入空间Fig. 2 Input space of uncertain variables 定义x方向的定位精度可靠度pr为 pr=Pr{gx(I)≤c}, (16) 根据全概率公式,可靠度pr可展开为 (17) 式中,证据变量Y属于焦元CYi的概率等于相应焦元的联合BPA: Pr{Y∈CYi}=mY(CYi)。 (18) (19) (20) (21) (22) 通过上述分析,可以获得工业机器人x方向定位精度可靠度的上下边界,即Pl和Bel: (23) (24) 同理,可采用相同步骤计算工业机器人在y方向Pr{gy(I)≤c}和z方向Pr{gz(I)≤c}定位精度可靠度,不再赘述。 由上述分析可知,采用常规方法对工业机器人定位精度进行可靠性分析时,需在证据变量的每个焦元上进行区间分析和概率可靠性分析,当证据变量维数较多时,计算效率会非常低。为了提高工业机器人概率-证据混合的定位精度可靠性分析计算效率,本文提出一种高效的工业机器人定位精度可靠性分析方法。 在实际工程中,工业机器人扭角的名义值一般为90°或者-90°,但是机器人受自身重量等外界因素的影响难以保证扭角为一个固定值。由于扭角值产生波动难以通过测量方式准确获得,根据文献[15]本文将工业机器人的扭角α1和扭角α3作为证据变量来研究,考虑到扭角波动范围很小,对应的识别框架变化范围较小,因此该识别框架内的子集变化范围也较小。基于以上分析,本文假设证据变量扭角α1和扭角α3在每个子区间上都服从均匀分布[15],由于每个子区间的变化都不大,该过程并不会造成较大的误差。将证据变量均匀化后,工业机器人系统内不确定参数输入变量均为随机变量,通过构建Kriging代理模型替代原功能函数进行可靠性分析,可在保证计算精度的前提下提高定位精度可靠性分析效率。 证据变量均匀化[7]是将证据变量转换为随机变量的过程,对于任意证据变量Yi,可进行如下转换 (25) 式中,fYi(y)为证据变量Yi均匀化处理后的概率密度函数,Aj是变量Yi的子区间,n(A)为子区间个数,Uj和Lj为子区间的上、下界,δj(yi)表示示性函数。当yi∈Aj时,δj(yi)=1;当yi∉Aj时,δj(yi)=0。 Kriging模型[16]由随机过程和回归模型共同组成,假设系统的响应值y(x)和自变量x之间函数关系表示为 y(x)=fT(x)β+z(x), (26) (27) 式中,xi和xj表示样本空间中的两个样本点,R(xi,xj)为样本点xi和xj之间的相关函数,其表达式为 (28) 式中,n为设计变量的维数,θk为各向异性参数,一般采用极大似然估计法[17]优化求解,dk表示数据点之间的距离。 集合Y和系数矩阵F可表示为 Y=[y1(x),y2(x),…,yn(x)]T, (29) (30) 利用试验的数据点和对应的响应值,可以得到相关系数矩阵 (31) 式中,N为实验数据的样本点数量。 通过广义最小二乘法[17],可以得到Kriging模型的多项式参数 (32) (33) 综上,可利用已知的模型系数和相关函数预测未知点的响应值 (34) 式中,rT(x0)=[R(x0,x1),R(x0,x2),…,R(x0,xN)]T,即为目标点与样本点之间的相关系数。 Lophaven等利用MATLAB软件编写了Kriging模型的DACE工具箱,该工具箱利用输入的实验样本点,可得到任意点处的响应值。 在证据变量的每个焦元上进行区间和概率可靠性分析,根据式和求出工业机器人定位精度可靠度的Pl和Bel。 综上,本文提出的高效概率-证据混合工业机器人定位精度可靠性分析流程如下: 1) 根据工业机器人模型,建立运动学方程,确定D-H参数和目标点,定义工业机器人定位精度的功能函数。 2) 对证据变量进行均匀化处理,将证据变量转换为概率变量,计算转换后概率变量的均值和标准差。 3) 利用拉丁超立方抽样,生成工业机器人不确定参数的初始样本,构建Kriging代理模型,并验证模型的准确性。 4) 分析工业机器人概率-证据混合定位精度可靠性,得到工业机器人定位精度可靠度区间的上、下界。 将本文提出的高效混合可靠性分析方法应用于某六自由度工业机器人以验证方法的有效性。工业机器人在长期工作过程,会因装配不当或自身重力等因素导致扭角名义值偏大或者偏小。本文将针对这种情况假设连杆长度和关节转角为概率变量,连杆扭角α1和α3为证据变量,对两种工况下某六自由度工业机器人进行定位精度可靠性分析。 如图3所示,某六自由度工业机器人安装在被加工工件的左侧,长期在该状态工作会由于自身重力作用造成连杆扭角α1和α3偏大。如图4所示,建立工业机器人运动学结构简图,其D-H参数如表1[15,18]所示。 图3 工况1工业机器人虚拟样机Fig.3 Virtual prototype of industrial robot in condition 1 图4 工况1工业机器人结构简图Fig.4 Schematic diagram of industrial robot structure in condition 1 表1 工业机器人D-H参数Tab.1 D-H parameters of the 6-DoF industrial robot 证据变量相应子区间的BPA通过概率模型获得[15],假设扭角α1和α3服从正态分布,均值μ1=μ3=1.576 mm,标准差σ1=σ3=0.002 mm。F(α1)为变量α1经截断后的累积概率分布函数,变量α1在每个子区间上对应的BPA为[15] BPA(i)=F(α1(i+1))-F(α1(i)), (35) 式中,i=1,2,…,n,α1(i+1)和α1(i)为第i个子区间的端点值。该工业机器人的不确定参数信息如表2[18]所示。 表2 工业机器人不确定参数Tab.2 Uncertain parameters of the industrial robot 定义工业机器人的空间目标点为P(1 183.1 mm,-353.5 mm,310.2 mm),由第3节可知,通过改变阈值c,即可根据式(13)~(15)获得相应的功能函数,利用本文提出的混合可靠性分析方法求解,可以获得对应的Bel和Pl。连接相邻阈值所对应的Bel和Pl可获得相应的累积分布曲线。同时,利用蒙特卡罗模拟方法(样本数105)计算每个功能函数所对应的概率值,将其计算结果作为参考解,结果如图5所示,部分可靠度结果列入表3。可以发现,对于同一个目标点P(1 183.1 mm,-353.5 mm,310.2 mm),x,y和z方向的定位精度不同。当Bel达到0.99左右时,x,y和z方向对应的阈值分别为4 mm,13 mm和1.2 mm。因此,在该工况下,z方向的定位精度最高,y方向的定位精度最低。在计算精度方面,以常规方法计算得到的结果作为参考解,本文提出方法和常规方法计算得到的Bel曲线和Pl曲线基本重合,表明本文提出方法具有较好的精度,且蒙特卡罗模拟法计算的可靠度曲线始终被包络在Bel曲线和Pl曲线中间。在计算效率方面,本文提出方法有明显优势,以x方向为例,常规方法计算表3中6个不同阈值下定位精度可靠度的CPU耗时约为343 s,而本文提出方法的CPU耗时仅为8.77 s。 图5 工况1定位精度可靠性分析结果Fig.5 Positioning accuracy reliability analysis results in condition 1 表3 工况1定位精度可靠性分析结果Tab.3 Reliability analysis results of positioning accuracy in working condition 1 如图6所示,某六自由度工业机器人安装在被加工工件的右侧,长期在该状态工作会由于自身重力作用造成扭角α1和扭角α3的角度偏小。运动学结构简图如图7所示,D-H参数如表1所示。 图6 工况2工业机器人虚拟样机Fig.6 Virtual prototype of industrial robot in condition 2 图7 工况2工业机器人结构简图Fig.7 Schematic diagram of industrial robot structure in condition 2 同样,假设扭角α1和扭角α3均服从正态分布[15],均值μ1=μ3=1.564mm,标准差σ1=σ3=0.002mm,证据变量相应子区间的BPA按上节介绍方法通过概率模型获得,扭角α1和α3的参数信息如表4[15]所示。 表4 认知不确定参数信息Tab.4 Epistemic uncertainty parameters 根据上节所描述的方法,定义该工况下工业器人的空间目标点为P(1 183.1 mm,-353.5 mm,310.2 mm),通过改变阈值c,即可根据式(13)~(15)获得相应的功能函数,求解得到Bel和Pl的累积分布曲线。蒙特卡罗模拟方法的样本数为105,计算结果如图8所示,部分可靠度结果列入表5。当Bel达到0.99左右时,x,y和z方向对应的阈值分别为4.5 mm,16 mm和1.6 mm。在该工况下,z方向的定位精度最高,y方向的定位精度最低。在计算精度方面,以常规方法计算得到的结果作为参考解,本文提出方法和常规方法计算得到的Bel曲线和Pl曲线基本重合,再次表明本文提出方法具有较好的计算精度。在计算效率方面,本文提出方法有明显优势,以y方向为例,常规方法计算表3中的6个不同阈值对应定位精度可靠度的CPU耗时约为406.82 s,而本文提出方法的CPU耗时仅需要9.34 s。 表5 工况2定位精度可靠性分析结果Tab.5 Reliability analysis results of positioning accuracy in working condition 2 图8 工况2工业机器人定位精度可靠性分析结果Fig.8 Positioning accuracy reliability analysis results of industrial robot in condition 2 本文针对一种常规的概率-证据混合可靠性分析方法计算效率低的问题,提出一种高效的概率-证据混合可靠性分析方法。与常规方法相比,本文提出方法的优势在于通过引入证据变量均匀化,将证据变量转换为随机变量,然后构建Kriging代理模型进行定位精度可靠性分析。通过工业机器人两种不同工况的分析,表明本文方法在处理概率-证据混合可靠性问题时,在保证具有较高计算精度的前提下,计算效率得到大幅提高,可以更高效地对工业机器人进行定位精度可靠性分析。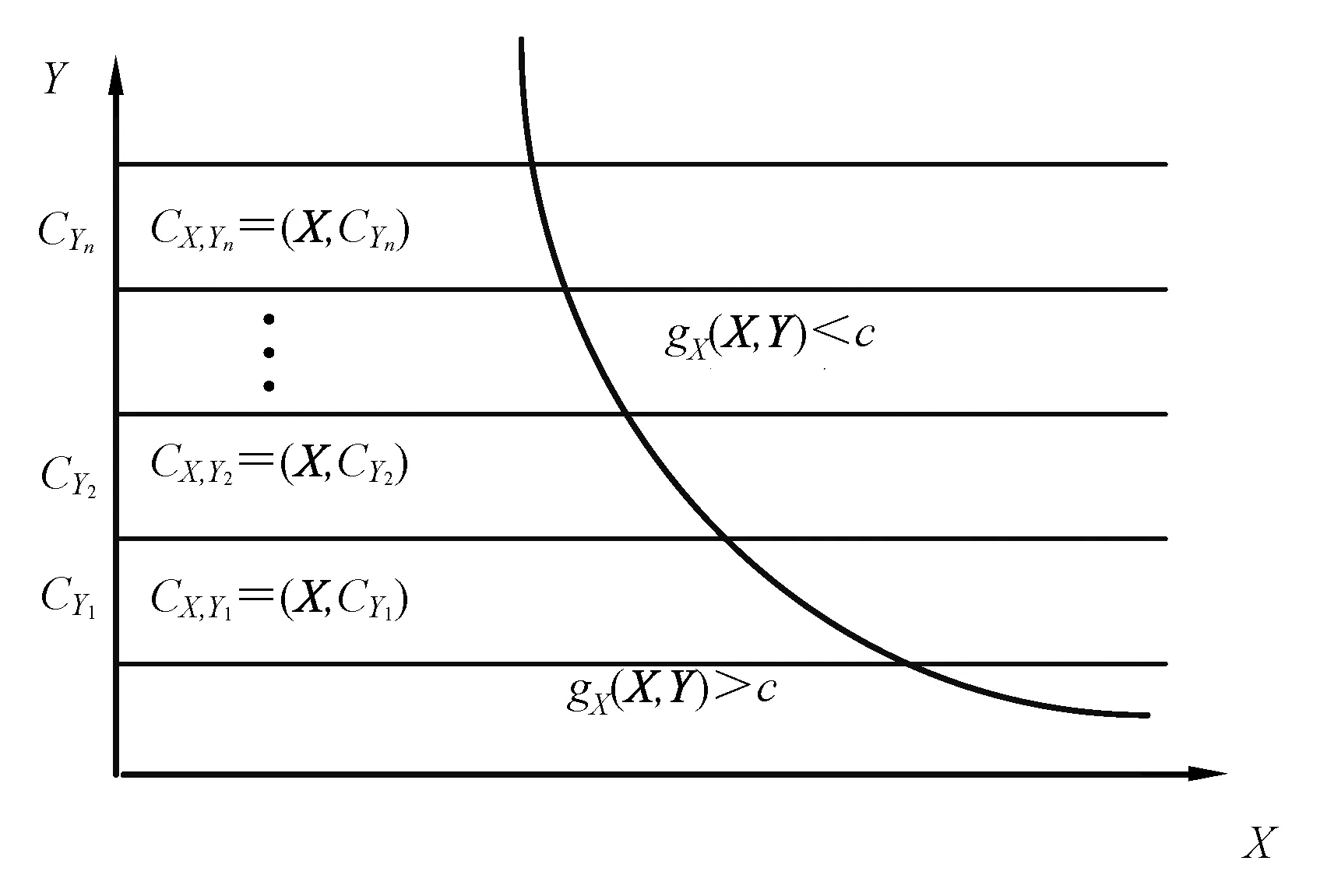


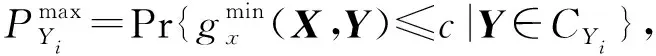
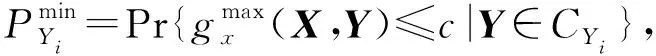

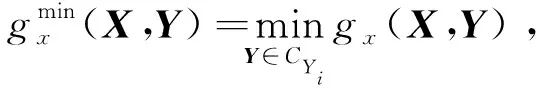
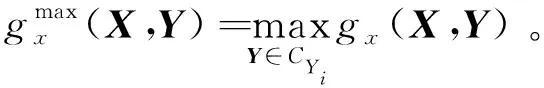
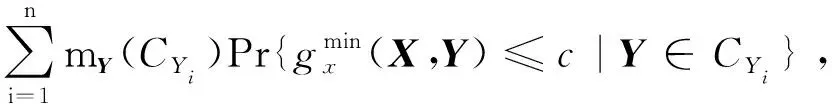
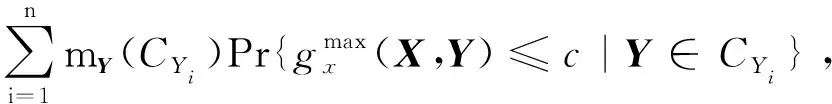
4 本文所提方法
4.1 证据变量均匀化

4.2 建立Kriging代理模型
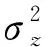
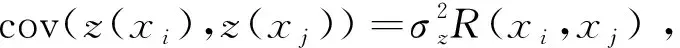
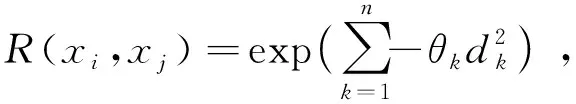


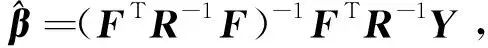
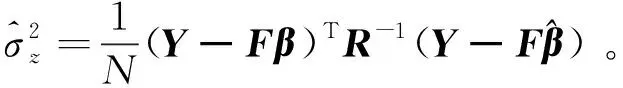

4.3 计算可靠性区间
4.4 算法流程
5 算例验证
5.1 工况1

5.2 工况2


6 结论
