基于模糊情感智能算法的动态电压恢复器研究
2022-08-01李永祥李梦达马梦琳
李永祥,李梦达,王 洋,马梦琳
(上海电机学院 电气学院,上海 201306)
0 引言
电压暂降作为目前有统计以来发生最频繁、对敏感负荷影响最大的电能质量问题[1-3],其良好治理方法一直是学者研究的重点。目前治理电压暂降的有效手段之一是在负荷侧安装电能补偿型电力电子装置[4-5],常用的治理装置有动态电压恢复器(Dynamic Voltage Restorer,DVR)、多功能电压暂降补偿装置、不间断电源等,其中DVR以其较低的成本和较好的补偿效果成为治理电压暂降问题最经济有效的电力补偿设备[6-8]。
在国内DVR研究领域中,优化控制方法往往是提升DVR系统补偿效果的关键,好的控制方法能在系统的稳定性、响应速度、补偿精度等方面得以很好的体现。目前常见的控制方法主要是PI控制[9-10],但当PI控制应用于非线性强耦合DVR系统时,系统的负载适应性较差,当负载发生扰动时,若不及时调整PI参数,系统的稳定性会受到影响。文献[11]通过模糊推理方法实现了PI参数的自整定,提高了系统的稳定性;文献[12]提出了一种PR控制方法,文献[13]提出一种基于PI和PR的复合控制策略,都在一定程度上提高了DVR 的补偿精度。文献[14]提出一种新的智能算法——情感智能算法,并将其应用于DVR系统。由于没有梯度运算和专家规则,情感智能算法具有结构简单、计算量小的优点,从而使DVR取得了很好的补偿效果。文献[15]将情感智能算法的模型进行简化,进一步提高了DVR的补偿速度,但文献[14-15]都忽略了情感智能算法中权值学习率对情感智能控制器的影响,如果学习率选取不恰当,系统控制性能会变差,从而影响补偿效果。
本文提出一种基于模糊情感智能算法的DVR系统,模糊情感智能算法通过模糊控制在线调整情感控制器中的权值学习率,在利用情感智能算法自整定优点的同时,又避免了因初始参数选择不当带来的系统不稳定情况,提高了控制器的稳定性和跟踪精度,优化了DVR电压补偿性能。最后,通过搭建MATLAB/Simulink 仿真模型,验证了所提改进方法的可行性和有效性。
1 DVR拓扑结构及原理
典型DVR拓扑主要分为4个单元:储能单元、逆变单元、滤波单元及耦合单元。储能单元提供补偿电压所需的能量;逆变单元将直流电压转化为需补偿的交流电压;滤波单元对输出补偿电压进行高次谐波分量的滤除;耦合单元将电网与DVR装置进行隔离,确保电网发生短路时不对DVR装置造成严重损坏。
本文DVR拓扑结构以三单相H桥逆变器为主体框架,储能单元为蓄电池,滤波单元为一般LC滤波器,DVR通过变压器串联接入电网,拓扑结构如图1所示。
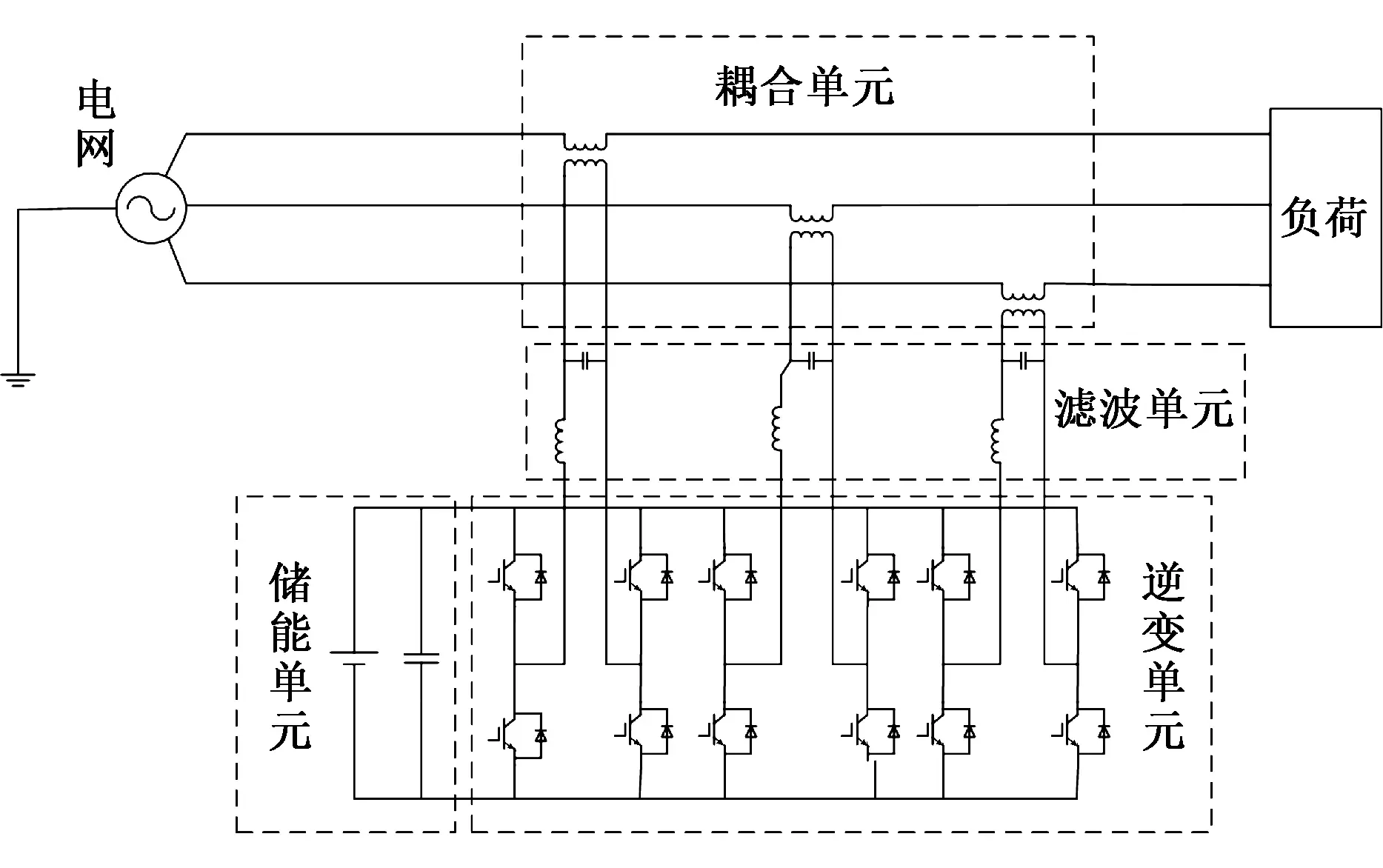
图1 DVR拓扑结构Fig. 1 DVR topology
由于采用三单相H桥结构为逆变单元,每一相的控制都是独立的,本文以A相为例,进行分析,其控制结构简图如图2所示。
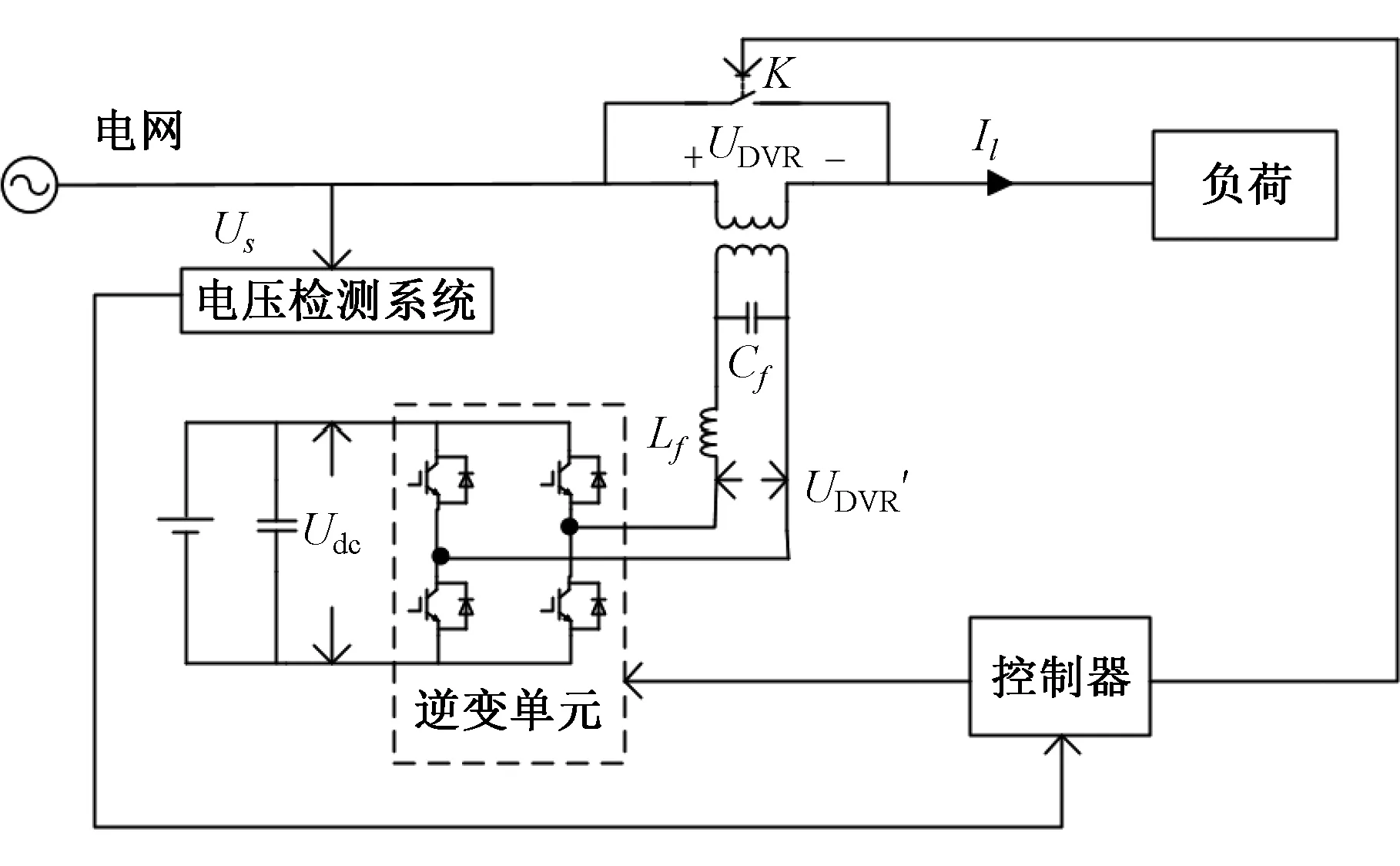
图2 控制结构简图Fig. 2 Control structure diagram
当DVR利用检测电路检测到电网发生电压暂降时,控制器控制转换开关K断开,DVR接入电网。与此同时,DVR利用检测电路检测出暂降后电压,通过和额定参考电压进行比对,选用合适的补偿方法获得期望补偿电压,控制器根据期望补偿电压产生相应PWM波形,控制逆变器开关的通断,从而输出补偿电压,保持负载侧电压稳定。
2 基于模糊情感智能的DVR系统
2.1 情感智能算法
情感智能算法主要是对大脑情感学习的一个建模过程,大脑中情感学习的主要部位是杏仁体,杏仁体通过接受来自不同感觉联合区的信息,记忆并巩固人的情感,可建立如图3所示模型来描述其学习过程。
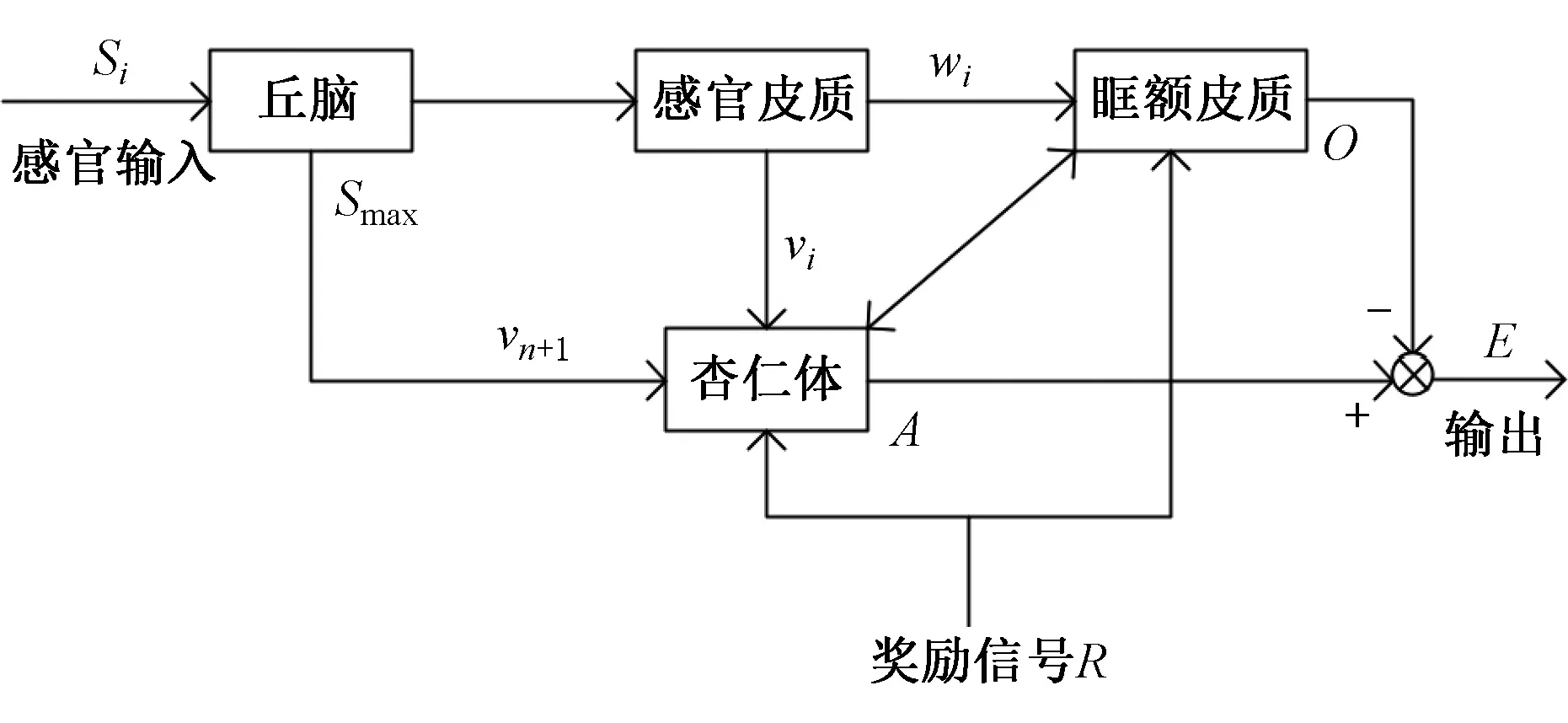
图3 大脑情感学习模型Fig. 3 Brain emotional learning model
图3中的丘脑、感官皮质、眶额皮质和杏仁体分别将接收到的感官输入信号Si和奖励信号R进行运算处理后,得到模型输出为
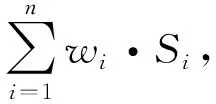
(1)
式中,νi、wi分别为杏仁体、眶额皮质的可调权值。
通过对权值νi和wi的更新调整,模型能实现对情感的更好学习。具体表达式为
Δνi=α·Si·max(0,R-A),(2)
Δνn+1=α·Smax·max(0,R-A),(3)
Δwi=β·Si·(E-vn+1Smax-R),(4)
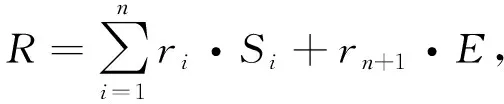
(5)
式中:i=1,2,…,n;Δνi为杏仁体的权值变化值;α为杏仁体的权值学习率;Δwi为眶额皮质的权值变化值;β为眶额皮质的权值学习率;ri为奖励信号R的可调权值。
2.2 DVR系统中情感控制器的设计
将情感智能算法应用于DVR控制中,其控制系统结构框图如图4,将DVR中期望补偿电压与反馈的实际补偿电压的差值传递到感官输入及奖励信号函数中,经过情感控制器处理后,输出理想补偿电压,最后通过PWM模块进行实际补偿电压的输出。
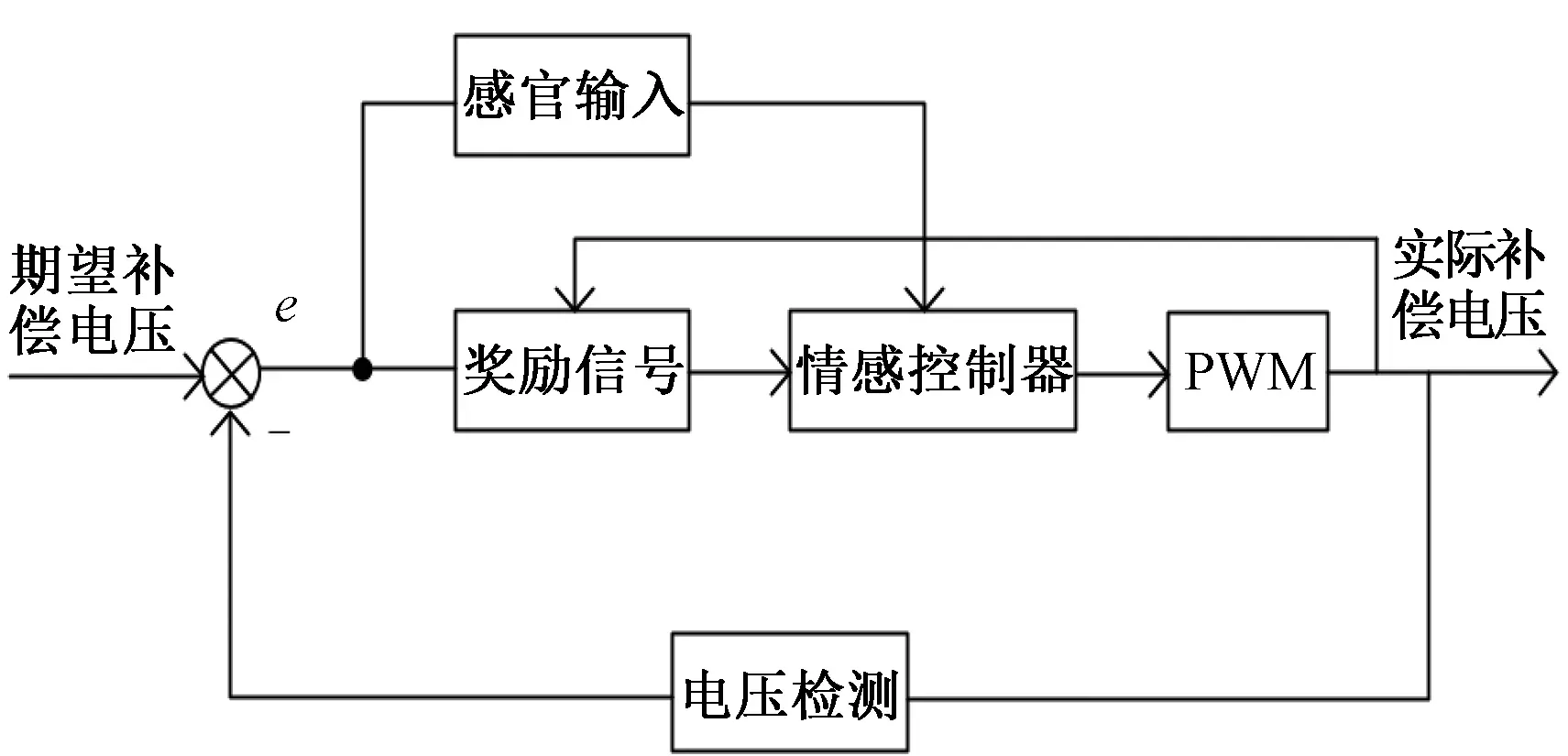
图4 情感智能DVR控制系统结构Fig.4 Structure of emotion intelligent DVR control system
本文选择感官输入信号为DVR中期望补偿电压与检测的实际补偿电压的差值及其差值的积分形式,即
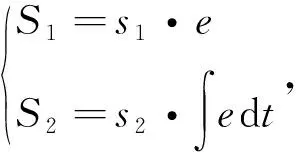
(6)
将式(6)代入式(1),可得到最终模型输出为
E=A-O=(ν1-w1)·s1·e+
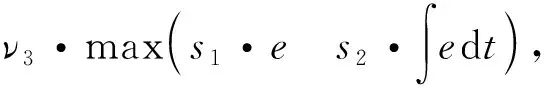
(7)
将式(6)代入式(2)~(5)中,得到权值变化值的表达式为
Δνi=α·Si·max(0,R-A)i=1,2,(8)
Δν3=α·Smax·max(0,R-A),(9)
Δwi=β·Si·(E-νn+1Smax-R)i=1,2,(10)
奖励信号R变为
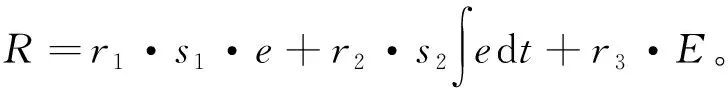
(11)
目前已知的情感智能算法中,其权值学习率都为定值,而由于所要应用的DVR系统有很强的非线性特点,固定的权值学习率势必会影响系统的调节品质。为了优化情感智能算法,使其更适用于DVR系统,本文采用模糊控制算法来对其权值学习率进行模糊调节,具体调节规则见下小节。
2.3 基于模糊控制的权值学习率调节
采用模糊控制算法调节权值学习率,主要难点在于模糊规则的制定。由于目前在情感智能算法的研究资料中,对权值学习率的调节文献较少,为了确定权值学习率的具体模糊调节规则,本文分别对杏仁体的权值学习率α和眶额皮质的权值学习率β取不同数值,按图4结构在Simulink中搭建基于情感智能的DVR系统模型,并进行系统阶跃响应实验。
学习率具体取值情况如表1所示。
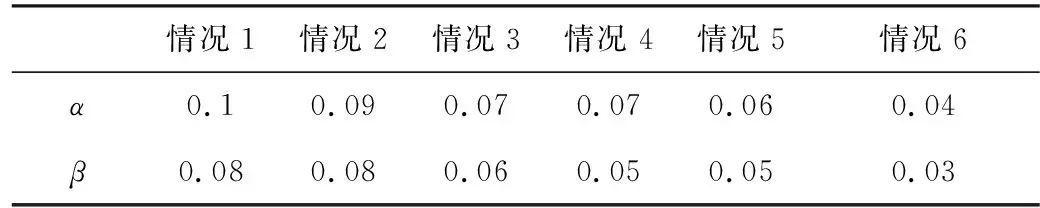
表1 学习率情况取值表Tab.1 Value of learning rate
情感控制器中的权重参数采用MATLAB/Simulink中的Signal Constraint模块进行优化。经优化后,感官输入的权重值s1、s2分别取为5.121、20.056;奖励信号的可调权值r1、r2、r3分别取为0.021、0.013、0.033。
经过阶跃响应验证,得到结果曲线如图5所示。
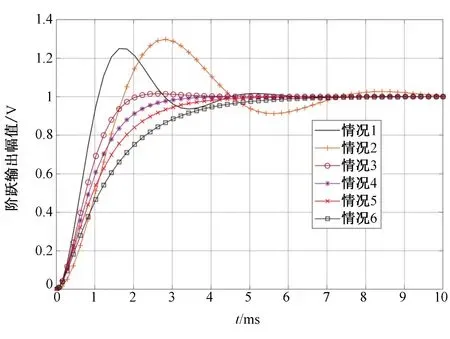
图5 不同情况学习率阶跃响应曲线Fig. 5 Step response curve of learning rate under different conditions
由图5可知:当权值学习率α和β过大时(如情况1、情况2,此时α和β值都大于0.07),系统的超调过大;当权值学习率α和β过小时(如情况6,此时α和β值都小于0.05),系统响应速度过慢;且在合适取值范围内,当权值学习率α不变,β减小时,系统的超调量变小;当权值学习率α减小,β不变时,系统的响应速度变慢。基于以上分析可知,权值学习率取值情况不同,其系统的响应效果不同,且权值学习率α对系统的响应速度影响较大,权值学习率β对系统的超调量影响较大。
根据系统阶跃响应曲线,进行模糊控制的权值学习率调节,具体步骤如下:
1) 输入、输出变量论域的确定
输入变量,即期望补偿电压与实际补偿电压的偏差e和偏差变化率ec的论域确定可通过进行多次基于情感智能算法的DVR系统仿真实验,找出其中最大的偏差及偏差变化率值,本文偏差e的基本论域取为[-10,10],偏差变化率ec的基本论域取为[-0.6,0.6];本文偏差e与偏差变化率ec的模糊论域均取为[-6,6]。
输出变量分别为权值学习率变化量Δα与权值学习率变化量Δβ,本文输出变量Δα与Δβ模糊论域变化范围均为[-6,6],实际变化范围均为[-0.02,0.02]。
2) 输入、输出变量模糊子集语言变量的选择
定义E,EC,ΔX,ΔY分别为e,ec,Δα,Δβ的模糊子集,其语言变量都选择为{NB,NM,NS,ZO,PS,PM,PB}。
3) 隶属函数的确定
隶属函数选择三角隶属函数,具体隶属规则如图6。
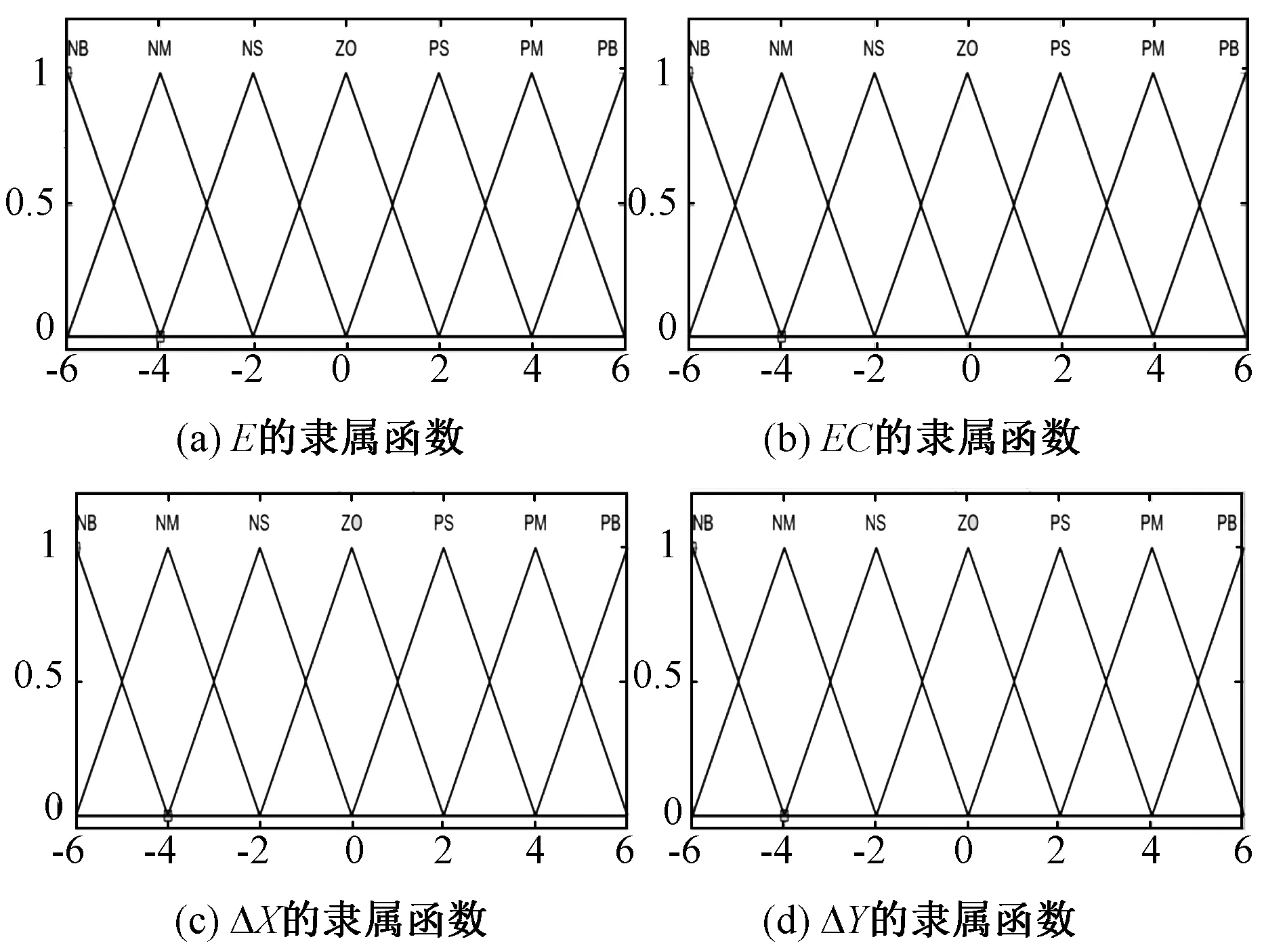
图6 输入输出隶属函数Fig. 6 Input and output membership function
4) 模糊推理规则的确定
模糊推理采用Mandani型模糊推理规则,具体推理规则如表2和表3。得到模糊推理规则曲面如图7所示。
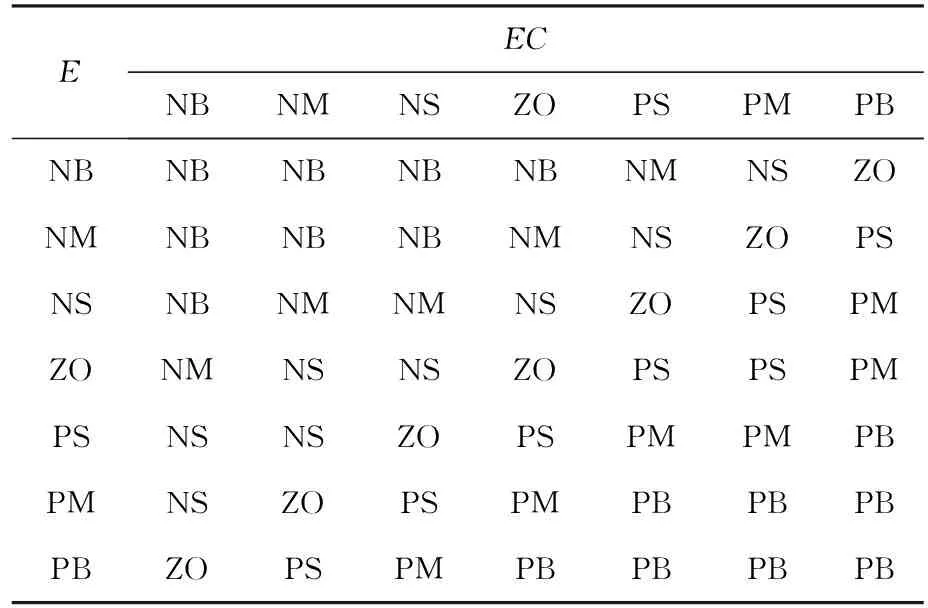
表2 ΔX的模糊控制规则表Tab.2 Fuzzy control rule table of ΔX
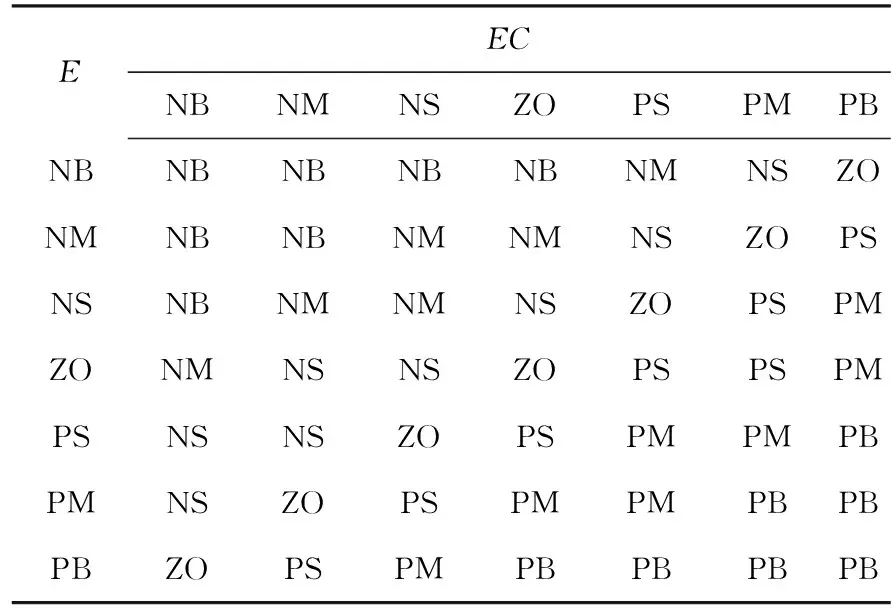
表3 ΔY 的模糊控制规则表Tab.3 Fuzzy control rule table of ΔY
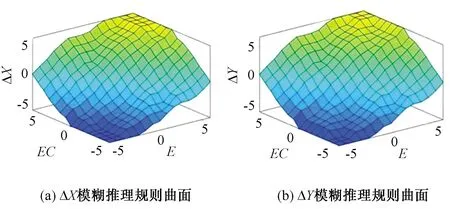
图7 模糊推理规则曲面Fig. 7 Fuzzy inference rule surface
由此,便可通过模糊控制完成对权值学习率的在线调节。
为验证模糊情感智能算法在DVR系统中的控制性能,搭建模糊情感智能DVR系统,并进行系统阶跃响应实验,取权值学习率α的初值为0.07,权值学习率β的初值为0.05,感官输入权重s1、s2分别为5.121、20.056,奖励信号的可调权值r1、r2、r3分别取为0.021、0.013、0.033。响应结果和无模糊控制情感智能DVR阶跃响应实验中的情况5做对比,对比结果如图8所示。
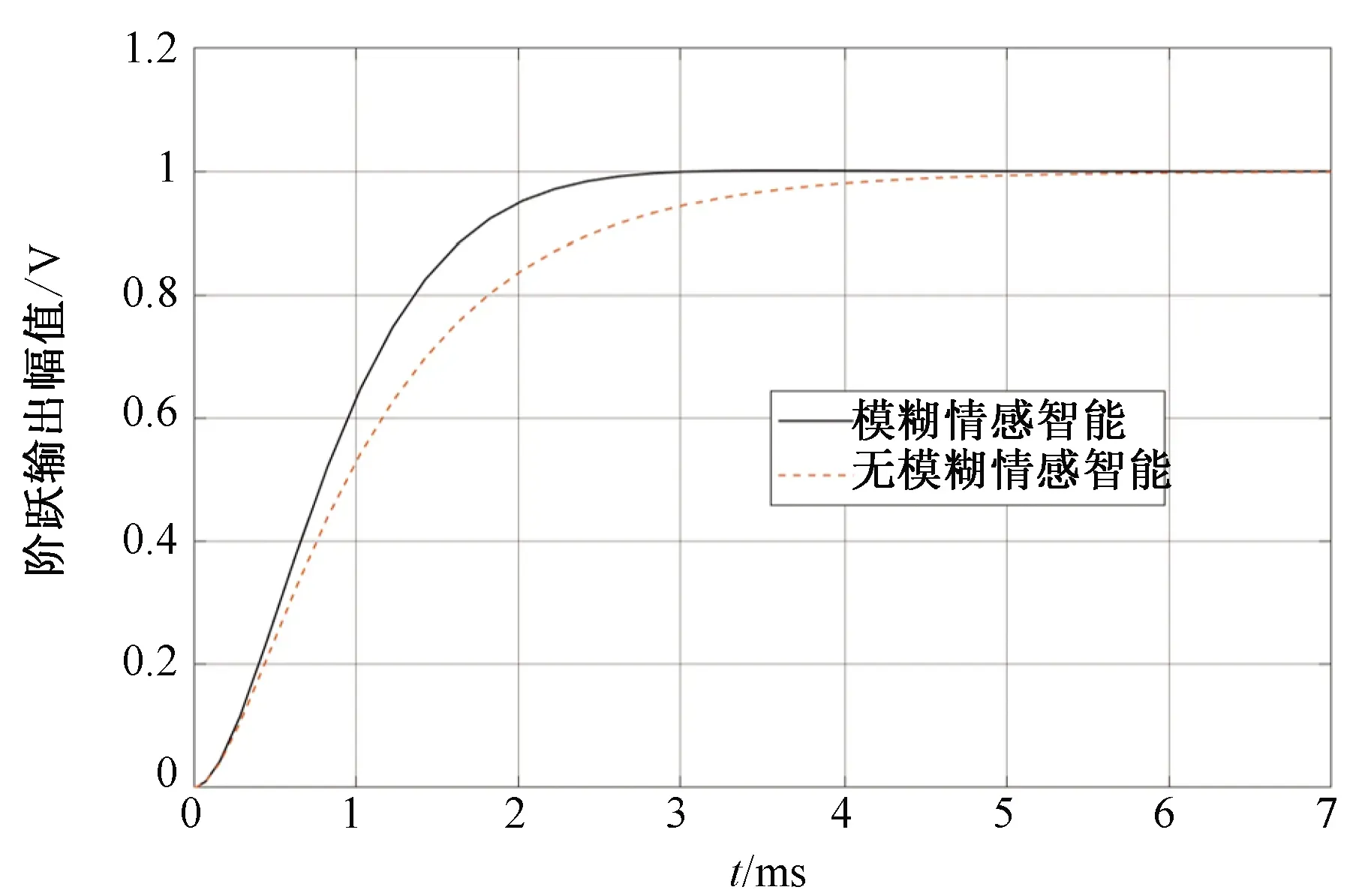
图8 模糊与无模糊情感智能阶跃响应Fig. 8 Fuzzy and non-fuzzy emotional intelligent step response
由图8可以看出,采用模糊情感智能算法,系统在3 ms左右达到稳定,相比于无模糊情感智能控制系统,其系统达到稳态时间更短,响应效果更好。
2.4 补偿控制流程
基于模糊情感智能的DVR系统补偿控制框图如图9所示。
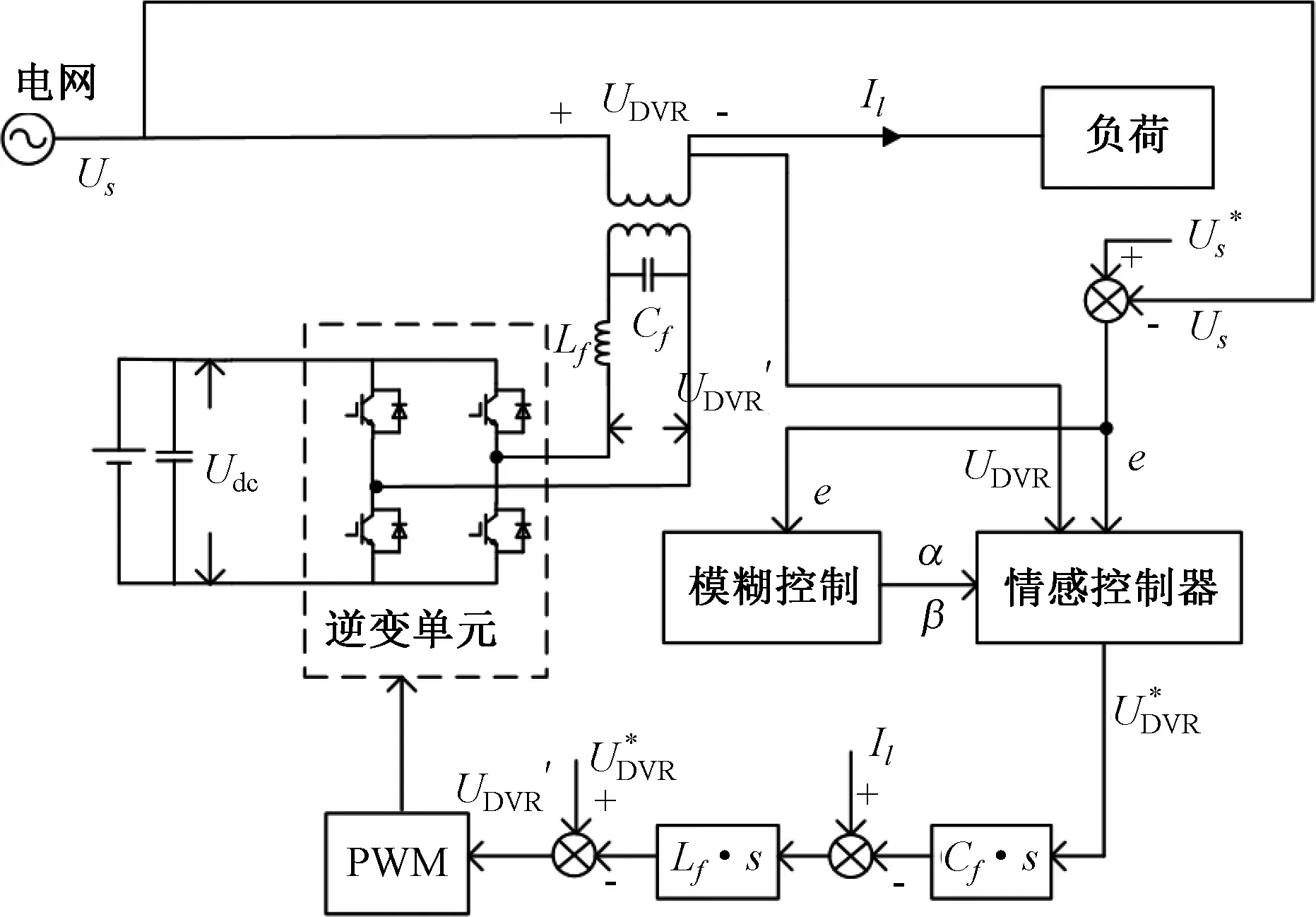
图9 补偿控制框图Fig. 9 Compensation control diagram
具体补偿控制由以下三个环节来完成:
1) 电压暂降检测及采样环节
检测电路实时检测电网电压,当电网电压发生暂降时,DVR装置接入电网,输出补偿电压。与此同时,检测电路完成对实际电网电压Us与DVR输出补偿电压UDVR的采样,并将其传给情感控制器。
2) 模糊情感控制环节
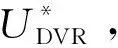
3) PWM逆变环节
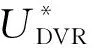
3 仿真
为了验证文中所提理论的正确性,在MATLAB/Simulink 仿真环境下对基于模糊情感智能控制的DVR系统以及无模糊情感智能控制的DVR系统进行仿真,具体仿真参数如表4所示。

表4 仿真参数Tab.4 Simulation parameters
1) 模糊情感智能控制优越性分析
为了验证文中所提基于模糊情感智能控制的DVR系统的优越性,设定在0.1 s到0.2 s间电网电压发生了30%的电压暂降,如图10所示,此时基于模糊情感智能和无模糊情感智能的DVR输出补偿电压波形和补偿后的负载电压波形如图11所示。
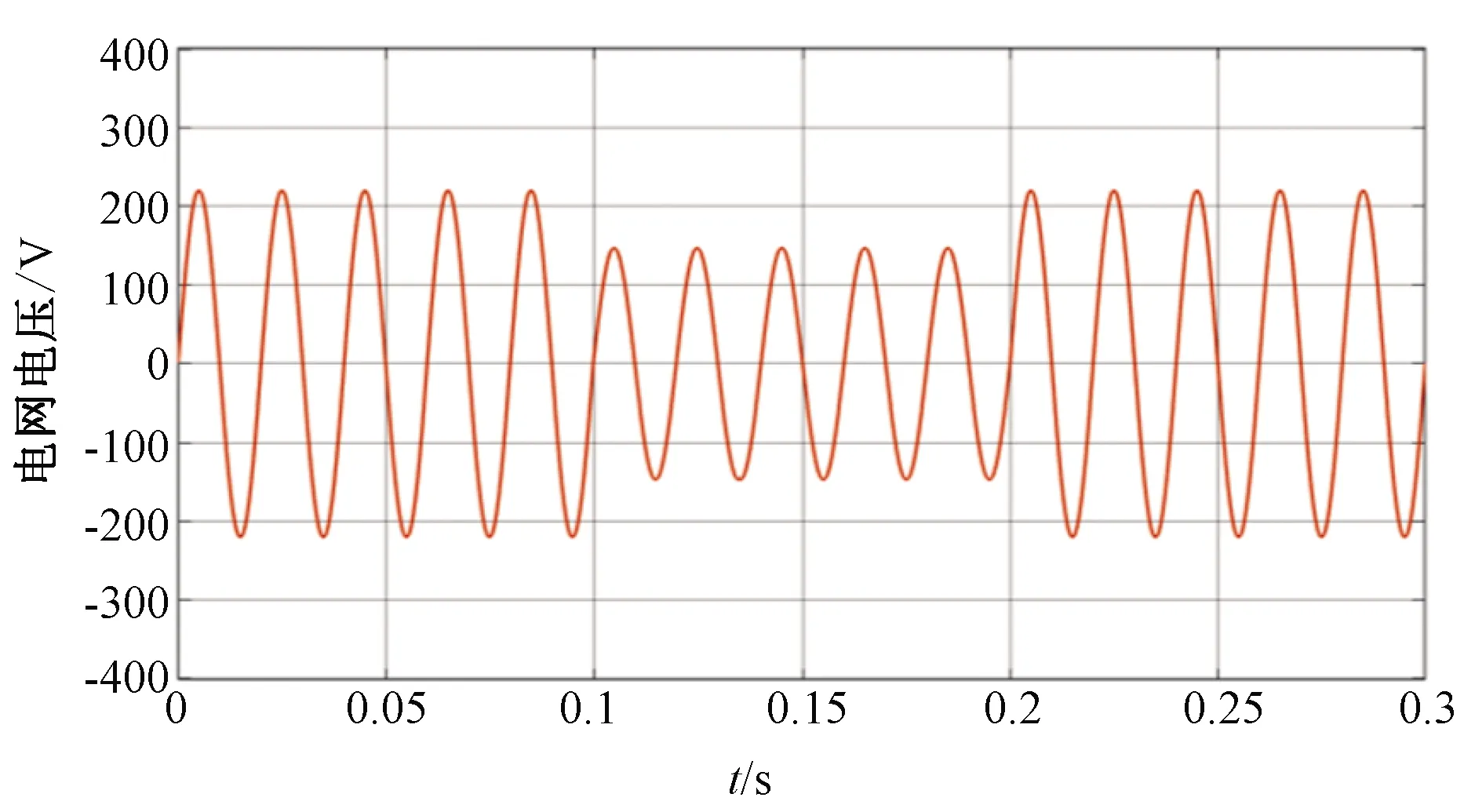
图10 电网电压波形(30%电压暂降)Fig. 10 Grid voltage waveform(30% voltage sag)
由图11可知,当电网电压从0.1 s开始发生暂降到0.2 s暂降结束时,基于模糊情感智能的DVR系统比无模糊情感智能的DVR系统能更快开始电压补偿,且补偿第一个波峰所需的时间更短,波峰的峰值更接近220 V,整个仿真周期负载电压也较为稳定。由此可知,通过模糊控制改进的情感智能DVR系统具有较好的系统稳定性和更快的响应速度,其系统补偿性能是更优越的。
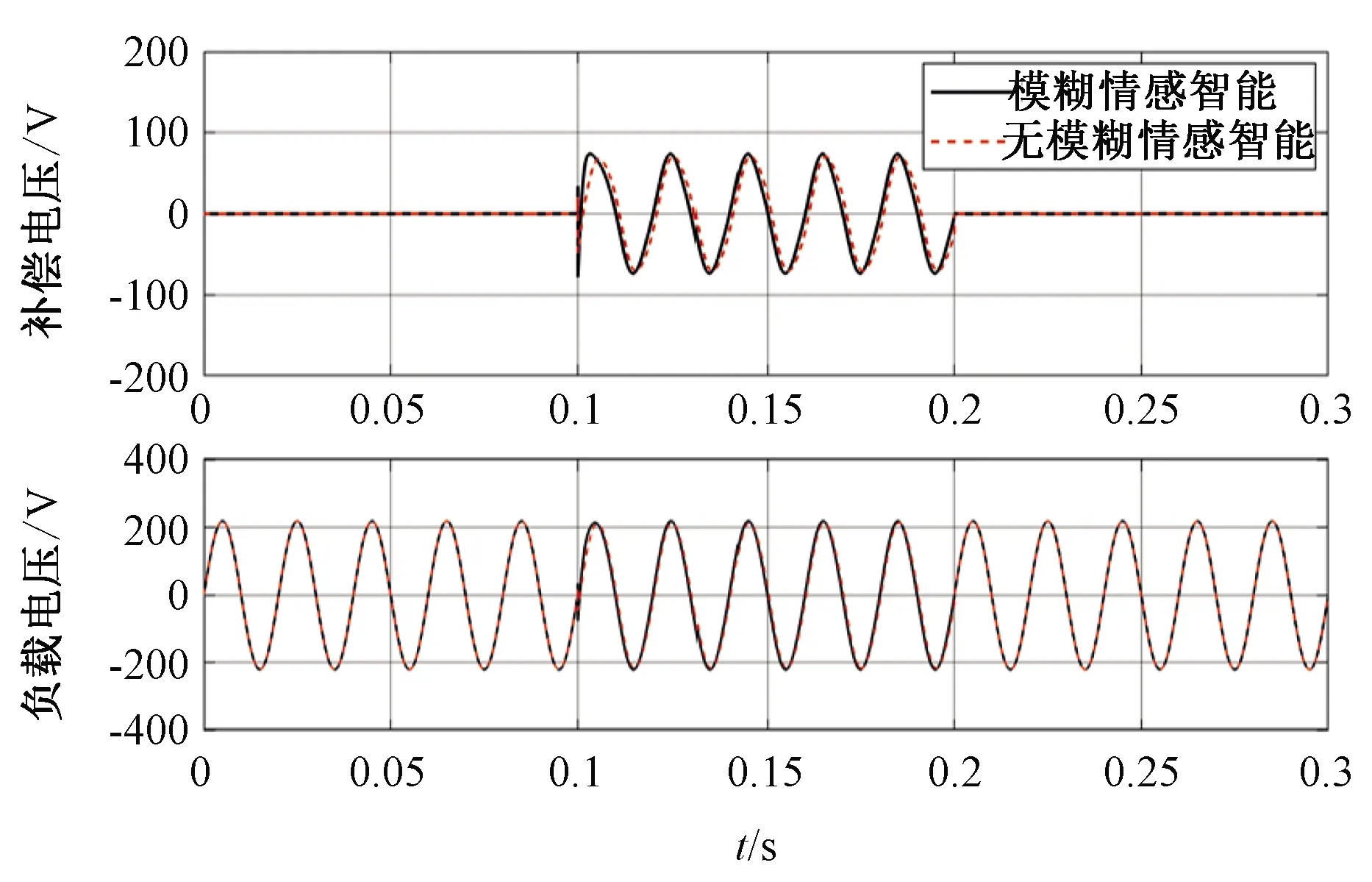
图11 负载与补偿电压波形(30%电压暂降)Fig. 11 Load voltage and compensation voltage waveform(30% voltage sag)
为了进一步验证所提改进算法的可行性,将原来设定成30%的电网电压暂降改成50%,如图12所示,此时基于模糊情感智能和无模糊情感智能的DVR输出补偿电压波形和补偿后的负载电压波形如图13所示。
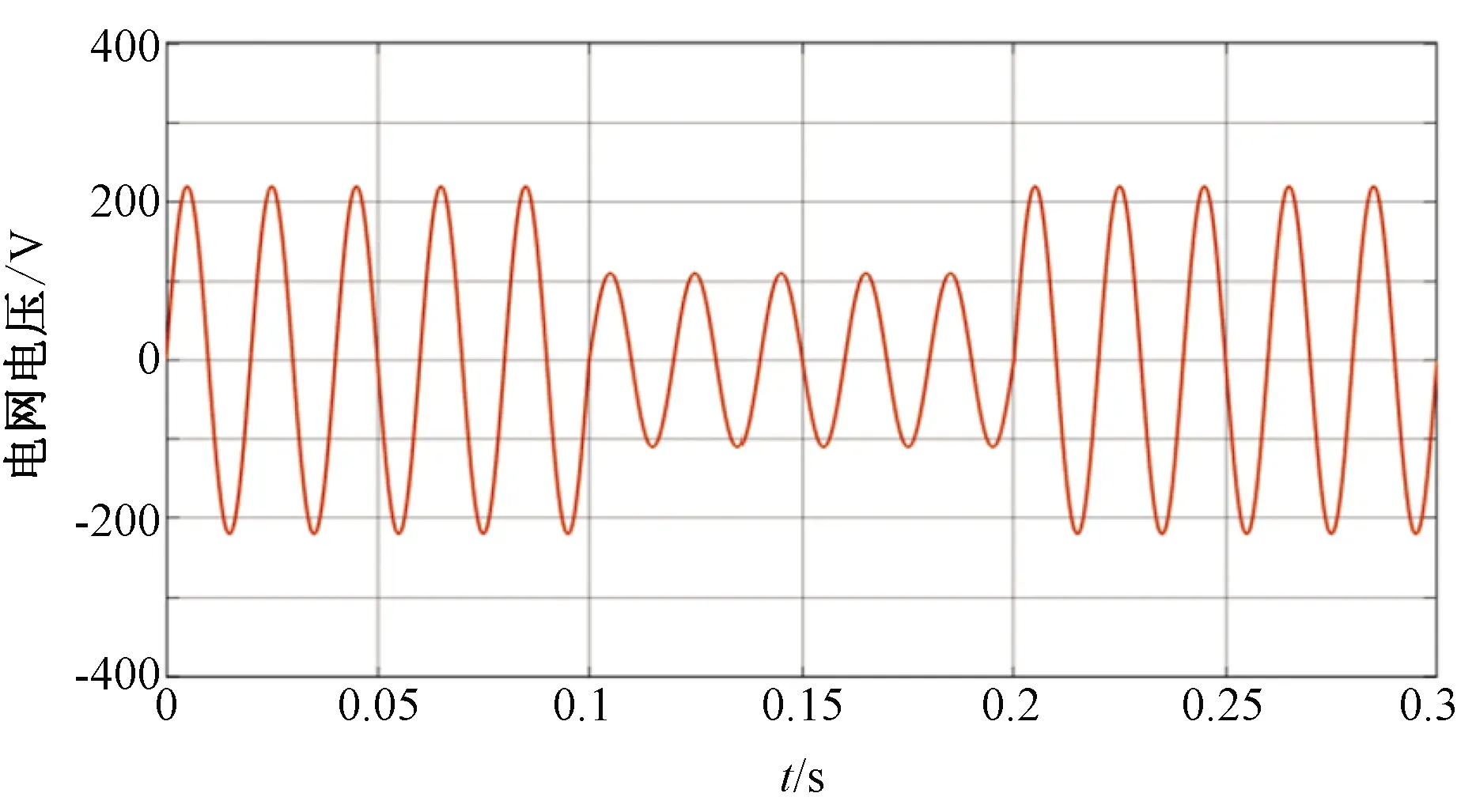
图12 电网电压波形(50%电压暂降)Fig. 12 Grid voltage waveform(50% voltage sag)
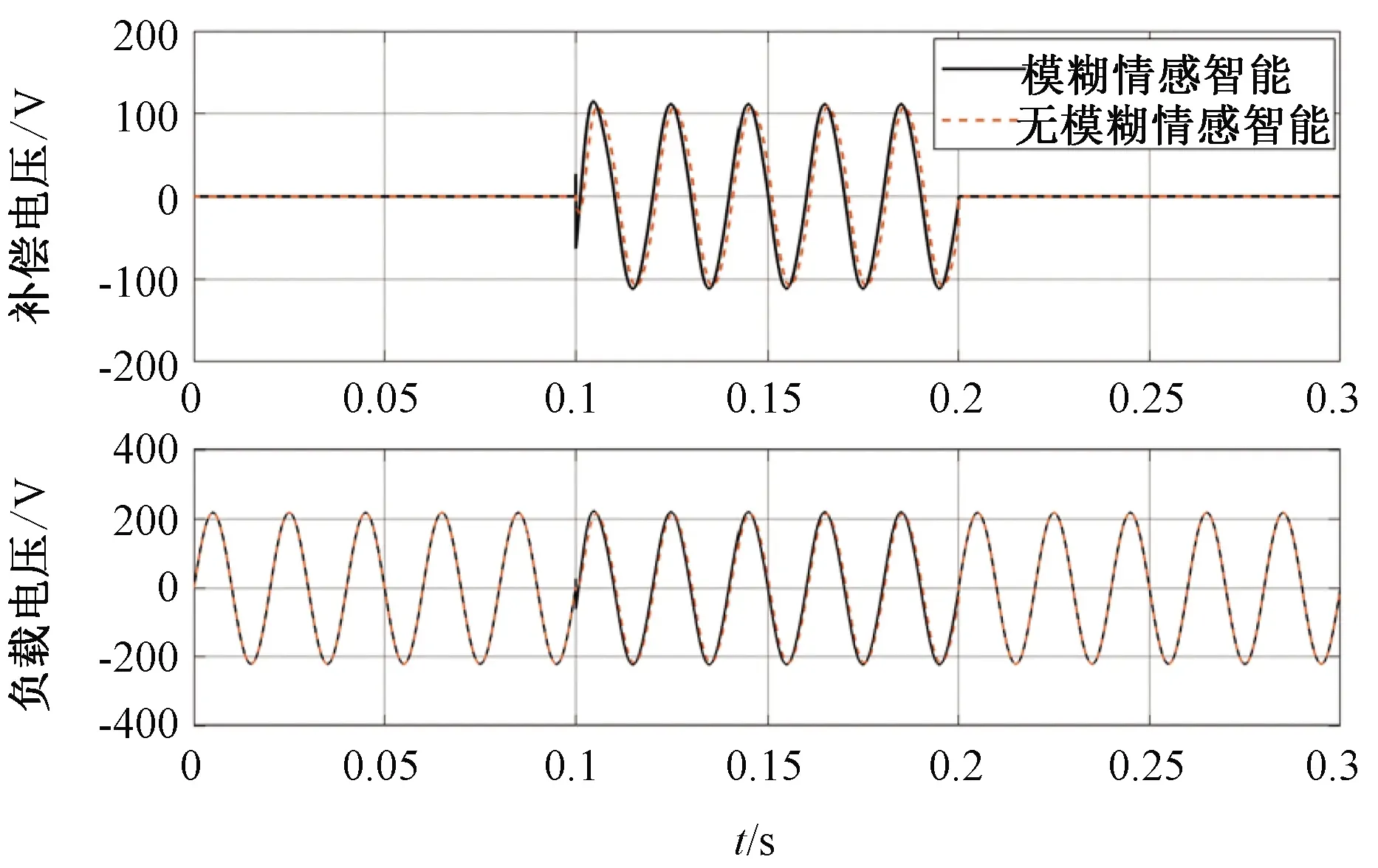
图13 负载与补偿电压波形(50%电压暂降)Fig. 13 Load voltage and compensation voltage waveform(50% voltage sag)
由图13可知,虽然电网电压的暂降程度加深了,但基于模糊情感智能的DVR系统与无模糊情感智能的DVR系统都能对跌落电压进行较好补偿,且同样地,基于模糊情感智能的DVR系统比无模糊情感智能的DVR系统补偿响应更快,同时电压恢复响应时间也有相应程度的缩短。由此便进一步验证了所提模糊情感智能算法的正确性。
表5列出了本文所提算法与文献[14-15]所提情感智能算法在电网电压暂降30%和50%时将电网电压恢复到额定电压的90%所需的时间。

表5 响应调节时间比较Tab.5 Response adjustment time comparisonms
由表5数据可以看出,本文所提基于模糊情感智能算法的DVR系统在响应调节时间上,相比其他文献的更短,发生50%暂降所需时间也只需5 ms,符合DL/T 1229中DVR响应时间不宜大于5 ms的要求。
2) 负载适应性分析
由于实际电网中的电压暂降对敏感负荷影响较大,本文对不同类型的敏感负荷进行仿真分析。图14和图15分别为模糊情感控制时阻感性负载(负载电阻10 Ω,负载电感25 mH)和阻容性负载(负载电阻10 Ω,负载电容40 μF)的仿真情况。
从图14和图15仿真结果可以看出,当电网电压发生暂降时,基于模糊情感控制的DVR都能在较短的时间内对电网电压进行补偿,且补偿效果比较理想,这表明文中所提模糊情感智能控制具有较好的负载适应性。

图14 阻感性负载情况波形Fig. 14 Resistive-inductive load waveform

图15 阻容性负载情况波形Fig. 15 Resistive-capacitive load waveform
3) 三相不平衡跌落分析
上述仿真结果都是在三相电压平衡跌落的情况下验证的,为了更好地验证文中所提基于模糊情感智能控制的DVR系统的可行性,设定在0.1 s到0.2 s间电网电压发生了三相不平衡电压跌落,其中A相电网电压发生了30%的电压暂降,B相电压发生了50%的电压暂降,C相电压发生了100%的电压暂降,图16为电网电压、补偿电压和负载电压的仿真图。
从图16的仿真结果可以看出,模糊情感智能控制DVR在三相电压不平衡跌落程度较大的情况下,仍能较好地输出补偿电压,使负载侧电压保持稳定。
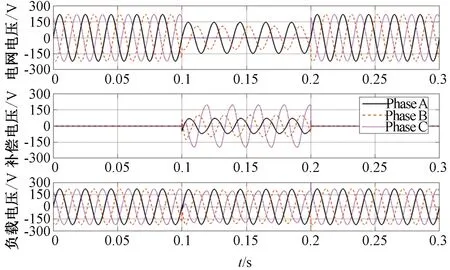
图16 三相电压不平衡情况波形Fig. 16 Three-phase voltage unbalanced drop waveform
4 结论
本文针对电网电压暂降问题,在已有的情感智能控制算法基础上,提出一种基于模糊情感智能算法的动态电压恢复器,并通过Simulink进行仿真验证,仿真结果表明:
1) 通过模糊控制算法实时调节权值学习率,能够进一步优化情感控制器的控制性能,提升DVR的补偿精度与补偿速度。
2) 相比于无模糊情感智能控制及简化情感智能控制的DVR系统,采用模糊情感智能控制的DVR系统其响应速度更快,补偿的波峰峰值更接近220 V,且恢复到90%额定电压所需的时间更短,控制在5 ms以内(满足DL/T 1229标准的要求),电压补偿效果更好。
3) 经过模糊控制算法改进后DVR系统,在不同负载及不平衡电压跌落情况下,补偿能力并没有受到影响,补偿效果仍较为理想。
