基于扩展的F展开法求孤子方程的广义解

孟 勇

(宁波大学 物理科学与技术学院，浙江 宁波 315211)

世界之所以色彩斑斓、变幻万千，是因为事物之间存在非线性联系。在非线性科学中，研究者从实际的非线性现象问题出发，按照物理规律，在合理的近似下建立相应的数学模型，然后通过研究这些数学模型来获得其相应的规律，从而用确定性的数学语言描述以及预测现象。在这些数学模型中，非线性偏微分方程占了很大一部分，求解这些偏微分方程并非易事，多年以来研究人员为此做了大量的工作，并取得了一系列重要成果，如反散射法[1]、达布变换法[2]、经典与非经典李群法[3]等。其中函数展开法[4-6]因其简单、直接、操作方便等优点，在解非线性偏微分方程中有着大量的运用。

文献[5-6]分别利用扩展的F展开法求解了Klein-Gordon方程和耦合Schrödinger-Boussinesq方程组的行波解。本文在文献[4]的基础上对该方法再次进行改造，将解的展开式对称延拓到负幂次，并对解的形式不加以行波解的限制，得到了更多类型的解。然后利用该方法求解了MKdV方程孤立波与Jacobi椭圆周期波之间的相互作用解，并通过设置相关参数绘制出其图形。最后求得了(2+1)-维BKK方程组的完全分离变量解，并通过给定解的形式得到了该方程组的特殊孤子解的结构激发。

1 扩展的F展开法

步骤1 对一个(1+1)-维非线性偏微分方程P(u,ux,ut,uxx,uux,…)=0使用行波变换ξ=kx-ωt(其中k与ω都是待定的常数)，把偏微分方程转换为常微分方程P(u,uξ,uuξ,…)=0。

步骤2 将u(ξ)展开为幂多项式

(1)

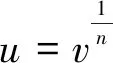
由文献[5-6]可知F′=C+λF+μF2,存在满足下列条件下的特殊解:

步骤3 将式(1)带入P(u,uξ,uuξ,…)=0，如果其中出现了F的导数项，就用F′=C+λF+μF2转化为F的幂多项式。再令该多项式中F各幂次的系数为零，导出关于ai(i=0,1,2,…,n),λ,μ,k,ω的一组代数方程。

步骤4 求解步骤3中的代数方程组，得到ai(i=0,1,2,3,…,n),k,ω的若干解。再将(Ⅰ)～(Ⅸ)代入式(1)就得到P(u,ux,ut,uxx,uux,…)=0的精确行波解。

在上述的一般F求解过程中，若放弃使用行波变换(1),而设P(u,uξ,uuξ,…)=0的解为

(2)

同样按照步骤3，将式(2)代入P(u,ux,ut,uxx,uux,…)=0,再运用F′=C+λF+μF2,可得到关于ai(i=-n,-n+1,…,n),φ(x,t)的一组偏微分方程。然后通过求解此方程组，得到P(u,ux,ut,uxx,uux,…)=0的解。

2 MKdV方程的相互作用解

MKdV方程

ut-6u2ux+u3=0

(3)

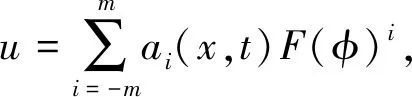
(4)

其中ai,φ都是x,t的函数。再将式(4)代入式(3),并运用式(2)进行化简合并为F(φ)的各次幂项之和，并且让各次幂系数为0，得到关于ai,φ的偏微分方程组。解此偏微分方程组得到了3组解与φ满足的偏微分方程条件。

(5)

(6)

(7)

最后将式(5)～(7)φt表达式代入式(4)就得到了MKdV方程3组解：

(8)

其中F=F(φ(x,t))为(Ⅰ)～(Ⅸ)中对应的表达式，此外在式(8)中φ(x,t)必分别满足式(5)～(7)φt表达式。然后通过对比式(8)u3与u1,u2可知，将解的展开式对称延拓到负幂次，可以得到更多形式的解。而且由于不设定φ(x,t)的具体表达式，因而可以极大程度上扩展该方程解的类型。

为求出该方程的孤立波与Jacobi周期波的相互作用解，所以构造φ(x,t)的表达式为

φ(x,t)=k1x+ω1t+W(ξ),ξ=k2x+ω2t。

(9)

其中W1(ξ)=Wξ,并满足椭圆方程

(10)

这里B0,B1,B2,B3,B4为待定系数。然后将式(9)代入式(5)φt表达式，并利用式(10)化简为W1的各次幂项之和，并且令各次幂系数为0，得到关于k1,k2,ω1,ω2,B0,B1,B2,B3,B4的代数方程组。求解方程组得

(11)

则可得到MKdV方程的孤立波与椭圆周期波的相互作用解。 最后再设置相关参数得到解的3D结构图与密度图，如图1所示。

(a)3D结构图(1)

(b)3D结构图(2)

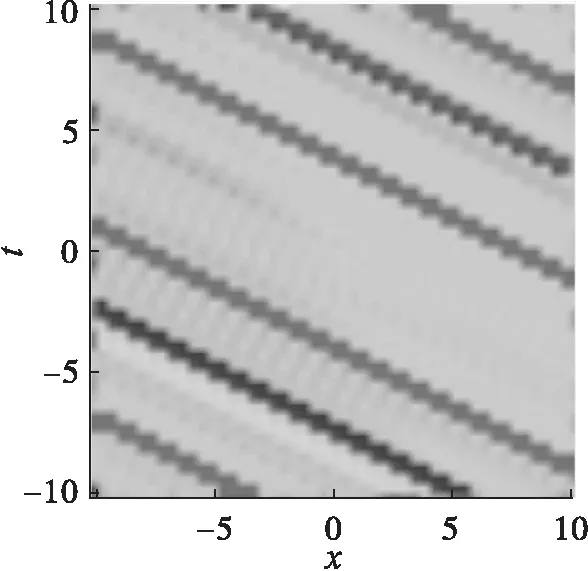
(c)密度图(1)

(d)密度图(2)

图1(a)(c)的参数为C=0,λ=1,μ=-1,k1=k2=1,ω1=0.5,B2=B3=1,n=0.1；图1(b)(d)的参数为C=0,λ=1,μ=-1,k1=2,k2=1,ω1=1,B2=B3=1,n=0.8。

3 (2+1)-维BKK方程组的分离变量解

对于用来描述带耗散的浅水波传播现象的(2+1)-维BKK方程组[11]

uty-uxxy+2(uux)y+2vxx=0,vt+vxx+2(uv)x=0,

(12)

为了求解方便，首先做变换v=uy,然后将v=uy代入式(12)第2式，得

uty+uxxy+2uxuy+2uuxy=0,

(13)

再利用齐次平衡原理确定展开的项数n=1。于是设u的展开式为

(14)

其中a-1,a0,a1,φ都是x,y,t的函数。设φ的完全的分离变量结构为

φ(x,y,t)=f(x)+g(y)+h(t)。

将上式与式(14)代入式(13),运用

F′=C+λF+μF2,

进行化简合并为F(φ)的各幂次，并且让各次幂系数为0，得到关于a-1,a0,a1,f,g,h的偏微分方程组。解此方程组，得到3组解：

将式上述3组解代入式(14)和v=uy就得到了(2+1)-维BKK方程组的对称延拓形式的完全分离变量解

(15)

其中F=F(φ(f+g+h))为(Ⅰ)～(Ⅸ)中对应的表达式。将式(15)v1表达式的参数设置为C=0,λ=1,μ=-1,再将

代入该式，选择f(x)=x2,g(y)=y2,h(t)=t,就得到了环形Lump孤子解，其图形如图2所示。改变f(x)，g(y),h(t),选择

则可得Lump孤子的分形结构解，如图3所示。由图3可以看出，在不同尺度下解的结构与形状完全相同或者基本不变，符合分形结构的定义，因此是分形结构解。

(a)3D结构图

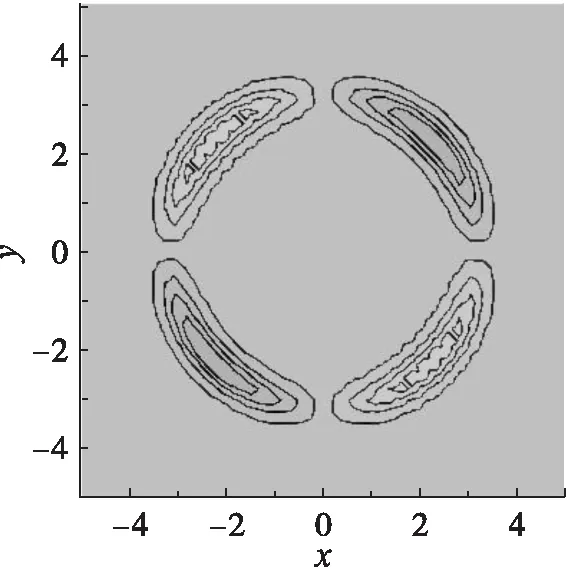
(b)等高线图

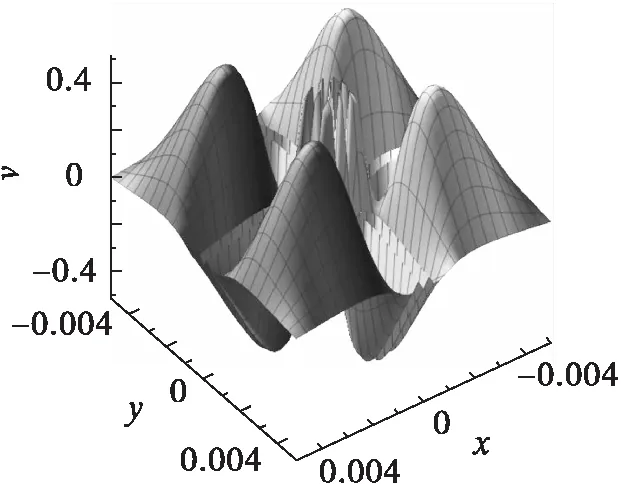
(a)3D结构图(1)

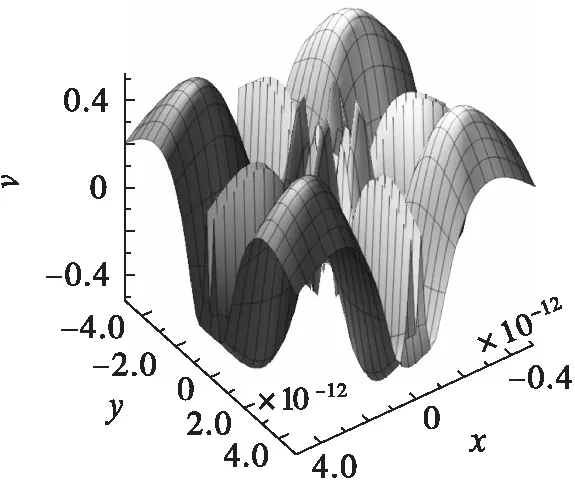
(b)3D结构图(2)

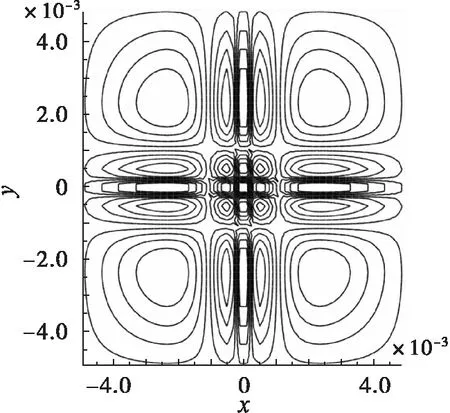
(c)等高线图(1)

(d)等高线图(2)

4 结论

为得到更丰富的非线性偏微分方程解的形式，对扩展的展开法进行改造。将原先的只向正幂次项展开对称延拓到负幂次项，并且将只能解出行波解改造为能够非限定形式的广义解。然后利用该方法求解MKdV方程与(2+1)-维BKK方程组，分别得到了孤立波与Jacobi椭圆周期波之间的相互作用解，以及完全分离变量解。该方法也可以很容易地运用到其他非线性偏微分方程中，给出更多形式的解。展开法的本质就是用已知解的微分方程中的高阶导数与低阶导数的关系，将已知方程的低阶项不断地去替换待求的微分方程的高阶导数项，以达到降阶的目的。因此，如果找到更多形式的已知解的微分方程，再配合对称延拓以及变量分离，就会有新形式的展开法及其可能的大量广义解。