航天器快速轨道机动过程中时变转动惯量实时辨识
2022-08-01魏远明王孟磊耿云海吴宝林
魏远明, 王孟磊, 耿云海, 吴宝林
1.国防科技大学空天科学学院,长沙 410073 2.北京宇航系统工程研究所,北京 100076 3.哈尔滨工业大学卫星技术研究所,哈尔滨 150001
0 引言
随着航天技术的发展和人类在太空的频繁活动,在地球周围,有许多种类繁多的航天器、火箭末级和空间碎片等,航天器通过各类传感器,探测空间中不同目标,进行空间态势感知,完成获取目标情报、对目标进行监视和侦察、太空环境检测、提供空间作战图等任务[1-2].此外,在空间对抗活动中,空间态势感知作为空间攻防对抗的基础,对于占领空间战略制高点至关重要[3].
在对目标监测或者抵近观测过程中,航天器存在快速轨道机动过程,推进剂会快速消耗,航天器抵近目标后,也需要通过操纵大型机械臂等技术,对目标完成相关在轨服务任务.这些轨道机动和航天器在轨服务活动,会造成航天器的质量特性参数产生变化.为了实现对目标的实时观测或者在轨服务,航天器必须具有快速姿态跟踪能力,许多控制律使用了转动惯量信息,用于补偿姿态动力学中的非线性特性,从而提高姿态控制精度.当转动惯量发生变化,原始控制器控制精度就会下降,甚至导致控制系统失效,需要及时对控制器中的转动惯量进行更新,保证控制力矩的合理性和准确性.
建立辨识航天器质量特性的回归模型的方式有两种:1)根据航天器动力学模型,利用力矩、角速度等信息辨识航天器质量特性[4-12];2)根据动量守恒、角动量守恒原理,对航天器或者空间机械臂等运动过程建模,建立辨识模型[13].利用这些回归信息,使用滤波方法(如卡尔曼滤波)、参数自适应、机器学习等方法估计航天器的质量特性,根据质量特性的标定结果,实时更新控制器中的相关参数,能够在航天器控制过程中施加更加准确的推力和力矩.目前对固定航天器转动惯量估计的文章较多,当航天器在进行快速轨道机动或者操纵大型机械臂等任务时,其转动惯量会变化,这不仅会影响航天器的控制精度,更加影响航天任务的正常实施.因此,需要设计合理的算法对动态转动惯量进行辨识.
文献[14]对含有时变转动惯量的航天器进行动力学建模,使用无迹卡尔曼滤波(unscented Kalman filter, UKF)实现了航天器时变转动惯量的辨识,但是相比于扩展卡尔曼滤波,UKF算法数学模型更加复杂、计算量也大,会较多占用航天器宝贵的计算资源;文献[15]分析了具有输入依赖特性的时变转动惯量,设计出一种自适应姿态跟踪控制律,实现了参数自适应辨识,但是文章没有考虑干扰力矩对参数辨识的影响;文献[16]使用磁力计、陀螺仪采集信息,采用了多模型自适应估计的方法估计时变转动惯量,但是没有考虑干扰力矩和测量噪声对于辨识精度负面影响;文献[17]提出了一种基于递推子空间算法的时变惯性矩阵参数辨识方法,根据航天器系统的原始状态空间模型提取了状态空间模型的相应块矩阵,进行递归得到航天器系统的时变转动惯量;文献[18]通过建模分析了加油过程中航天器转动惯量变化对航天器姿态的影响,但是没有继续依托模型给出转动惯量辨识算法.此外,以上文献中转动惯量辨识相关算法均将航天器角加速度作为精确已知信息用于参数辨识,而实际中,航天器角加速度无法直接测量,需要对角加速度值进行估计.
本文转动惯量作为待辨识参数,考虑前后两个时刻参数的变化过程,重新推导扩展卡尔曼滤波(extended Kalman filter, EKF)中的卡尔曼预测误差协方差矩阵.设计角加速度观测器,以航天器角加速度作为EKF滤波模型中所需的系统输出信息,对参数预测值进行修正,实现了对当前时刻参数的估计.最后,实时更新控制器中的转动惯量信息,执行机构能够施加更加精准的控制力矩,保证姿态跟踪精度.
本文主要在以下方面对转动惯量辨识研究做出了贡献:1)设计了线性状态观测器估计航天器的角加速度,用于辨识转动惯量;2)根据参数变化,重新推导了EKF中的卡尔曼预测误差协方差矩阵,在算法中对参数的时变特性进行了补偿.相比于文献[14]和[17],本文使用的EKF算法更加节省航天器的计算资源;相比于文献[15-16]和文献[18],本文没有对转动惯量进行过多限制,更具备实用性.本方法有效实用、容易实现,具有工程应用价值.
本研究的主要算法结构如图1所示.航天器的姿态测量和确定系统实时测量航天器的姿态信息.根据测量的航天器角速度信息,使用角加速度观测器估计航天器的角加速度.根据航天器的角速度测量值、角加速度估计值和控制力矩,使用改进的扩展卡尔曼滤波器实时辨识航天器的转动惯量.将航天器姿态信息和转动惯量估计值反馈到控制器中,计算姿态跟踪所需力矩,再由执行机构完成航天器姿态控制.

图1 基于时变转动惯量辨识的航天器姿态控制结构图Fig.1 Block diagram of spacecraft attitude control with time-varying moment of inertia identification
1 系统模型
航天器的姿态动力学模型和四元数表示的姿态运动学模型为
(1)
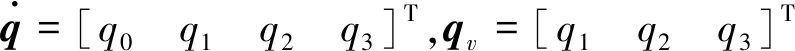
a×表示叉乘矩阵
假设期望姿态四元数为qd、期望角速度为ωd,则航天器期望姿态四元数变化过程可以表示为
航天器的姿态四元数q、期望姿态四元数qd和误差姿态四元数qe之间的关系为
q=qd∘qe
其中,符号°表示四元数乘法.
航天器的姿态角速度误差为
ωe=ω-C(qe)ωd
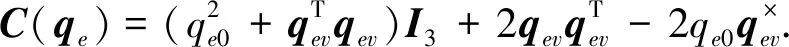
以航天器姿态误差角速度ωe和姿态误差四元数qe表示的航天器的动力学模型和运动学模型为

(2)
2 时变转动惯量辨识
与航天器动力学模型相关的转动惯量辨识需要用到航天器角加速度信息,许多航天器的角加速度无法直接测量获得,需要进行估计.通常情况下,可以通过航天器的动力学模型建立状态观测器估计角加速度信息.但是,当航天器快速轨道机动或操纵机械臂时,转动惯量未知,无法准确构建姿态动力学模型用于角加速度估计.
考虑使用可测的航天器角速度,通过设计线性角加速度观测器,实现航天器角加速度的估计,用于航天器转动惯量辨识.然后,根据航天器动力学模型中待辨识转动惯量的时变特性,对EKF算法[19]进行改进,将转动惯量的变化过程参数化,得到了适用于时变转动惯量辨识的滤波算法.
2.1 角加速度估计


(3)
rank([CTATCT]T)=2,说明该系统是完全可观测的,设计线性状态观测器如式(4)所示

(4)
其中,G=[g1g2]T是线性观测器增益,用于设置状态矩阵(A-GC)的特征值.
通过合理配置观测器状态矩阵(A-GC)极点位置,可以使得状态观测系统(4)稳定并实现对航天器的角加速度进行观测,根据极点位置可以解得g1、g2的具体数值.
2.2 滤波辨识算法
令θ=[JxxJyyJzzJxyJxzJyz]T,将其作为待辨识参数,对于时变的转动惯量,每个采样时刻,转动惯量的变化过程可以描述为
θk=θk-1+Δθk
(5)
其中,θk是第k时刻转动惯量真值,θk-1是第k-1时刻转动惯量真值,Δθk是转动惯量变化量.
(6)
其中,v∈R3定义为干扰项,包含了转动惯量导数对航天器动力学的影响、航天器干扰力矩和角加速度的观测误差.
使用EKF进行参数辨识,每次迭代过程中,需要先对参数进行预测,在当前时刻,设置参数的预测值为
(7)

在EKF算法中,卡尔曼预测值误差协方差矩阵能够表现预测值误差中包含的参数变化和预测模型偏差.通过对预测值误差的协方差矩阵进行推导,可以将参数变化和模型偏差造成的影响从协方差矩阵中分离出来,预测误差协方差矩阵为

(8)
根据式(5),有

(9)
将括号中的内容展开,分离出变化量对应的协方差矩阵,可得

(10)
Pk|k-1=Pk-1|k-1+ΔPk
(11)
通过设置ΔPk的值,可以在参数辨识过程中表现航天器的转动惯量的变化.
参数预测值相比于当前时刻的真值还存在较大误差,根据系统的量测信息和输出方程,使用含有参数变化量信息的预测误差协方差矩阵对预测结果进行修正,同时计算估计值的误差协方差矩阵,用于下一次迭代.根据EKF算法,需要计算输出方程(6)对应的雅可比矩阵,为
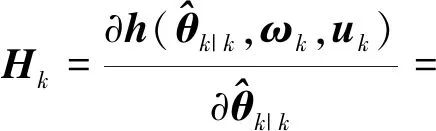
(12)

(13)
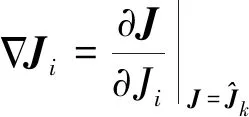
结合EKF算法结构,进行整理、总结,可以得到如下参数辨识模型:

(14)

在滤波过程中,转动惯量变化是未知的,需要通过预测误差协方差矩阵反映其变化过程.在某段时间内航天器轨道机动和机械臂变化程度不同,对应转动惯量的变化剧烈程度也不同,在使用设计的EKF算法辨识动态转动惯量时,可以设置参数变化量协方差矩阵的估计值为不同的固定对角阵,比如ΔPk=I6,从而表现转动惯量的变化.此外,干扰项v包含的量均是未知的,仍将R当作随机量的协方差矩阵估计值.
3 控制律
使用含有模型补偿项的传统类PD控制律[20]进行航天器姿态跟踪.转动惯量的变化会导致控制力矩的计算出现偏差,可以将转动惯量的滤波估计值实时反馈至控制器中,补偿转动惯量变化带来的控制误差,得到更准确的控制力矩.当前时刻的控制力矩为

(15)

4 仿真结果
根据设计的算法,进行角加速度估计、动态转动惯量辨识和姿态跟踪的相关仿真和结果分析.在跟踪监测时,航天器进行姿态跟踪,需要满足持续激励条件[21],以保证航天器转动惯量的有效辨识,设置航天器姿态期望角速度为
部分仿真参数设置如表1所示.
设置航天器转动惯量同时存在分段线性变化和正弦变化,转动惯量变化为ΔJ(kg·m2)
ΔJ=ΔJ1+ΔJ2
其中,航天器转动惯量分段线性变化ΔJ1(kg·m2)用来模拟快速轨道机动中燃料的消耗或补充等情况对转动惯量的影响,转动惯量正弦变化ΔJ2(kg·m2),用来模拟大型机械臂操纵等情况对转动惯量的影响

表1 仿真参数设置Tab.1 Simulation parameters setting
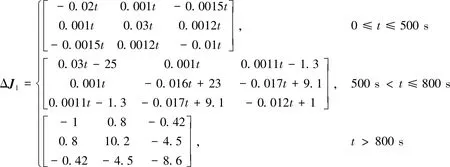
4.1 角加速度估计
航天器角加速度的估计结果如图2所示,从图中可知,使用状态观测器(4)能够实现航天器角加速度估计,在5 s之后,角加速度估计误差最大值为0.012((°)/s2),对比角加速度估计曲线可知,该误差大小约占幅值的3%,不确定度足够小,角加速度估计效果良好,可以用于航天器转动惯量辨识.

图2 转动惯量变化时角加速度估计结果Fig.2 The angular acceleration estimation with time-varying inertia matrix
4.2 转动惯量辨识
分别采用本文算法、常规EKF算法和梯度下降法3种方法,进行转动惯量辨识,对比分析本文算法的有效性,其中,梯度下降法的自适应律为
(16)

航天器的转动惯量真值为J=J0+ΔJ,分别使用以上3种方法对该时变转动惯量进行实时辨识.惯量矩阵主对角线元素的辨识结果及误差如图3所示,惯量矩阵非主对角线元素的辨识结果及误差如图4所示.
从图3和4的辨识结果可以看出,相比于常规EKF算法,本文的算法能够有效实现动态转动惯量的辨识,相比于梯度下降法,本文算法的辨识效果也更好.从图3(a)和图4(a)中可以看出来,在300 s之后,本文算法的参数辨识误差能够稳定在±1.5(kg·m2)以内,辨识效果良好.
4.3 姿态跟踪效果
根据式(14)中改进的EKF算法对时变航天器转动惯量的辨识结果,实时更新控制律(15)中的转动惯量信息,完成前馈补偿,进行姿态跟踪控制.为了表现时变转动惯量辨识对航天器姿态跟踪精度的影响,分别将控制器中转动惯量设置为固定值和实时估计值,进行对比仿真.
当控制器中转动惯量恒定不变时,姿态跟踪的角速度误差和姿态角误差如图5所示.当控制器中转动惯量实时更新时,姿态跟踪的角速度误差和姿态角误差如图6所示.

图3 惯量矩阵主对角线元素辨识结果及误差Fig.3 The identification results and errors of the moment of inertia
由图5可知,随着转动惯量相对于初值的变化量的增加,航天器的控制精度会逐渐变差,最大角速度误差甚至达到了0.7((°)/s),最大姿态角度误差约为1.8°,姿态跟踪效果很差.由图6可知,实时更新控制律中的转动惯量,航天器姿态跟踪过程能够在30 s内实现稳态,姿态跟踪角速度误差能够控制在±0.035((°)/s)以内,姿态角误差可以控制在±0.22°以内.
通过对图5和6的对比分析,说明实时辨识转动惯量并更新控制器参数,有利于保证航天器的姿态跟踪精度.
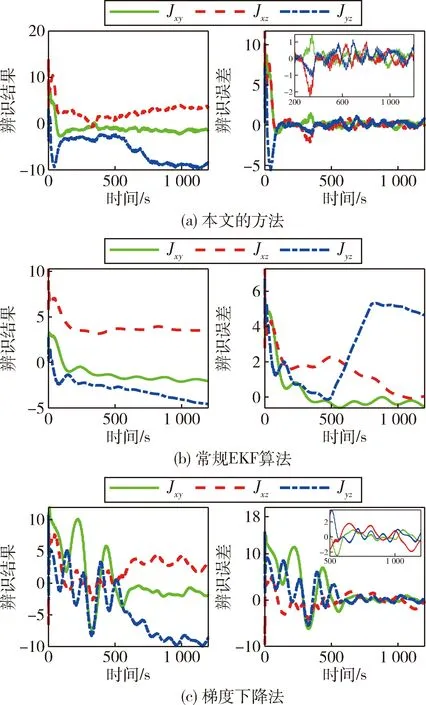
图4 惯量矩阵非主对角元素辨识结果及误差Fig.4 The identification results and errors of the product of inertia
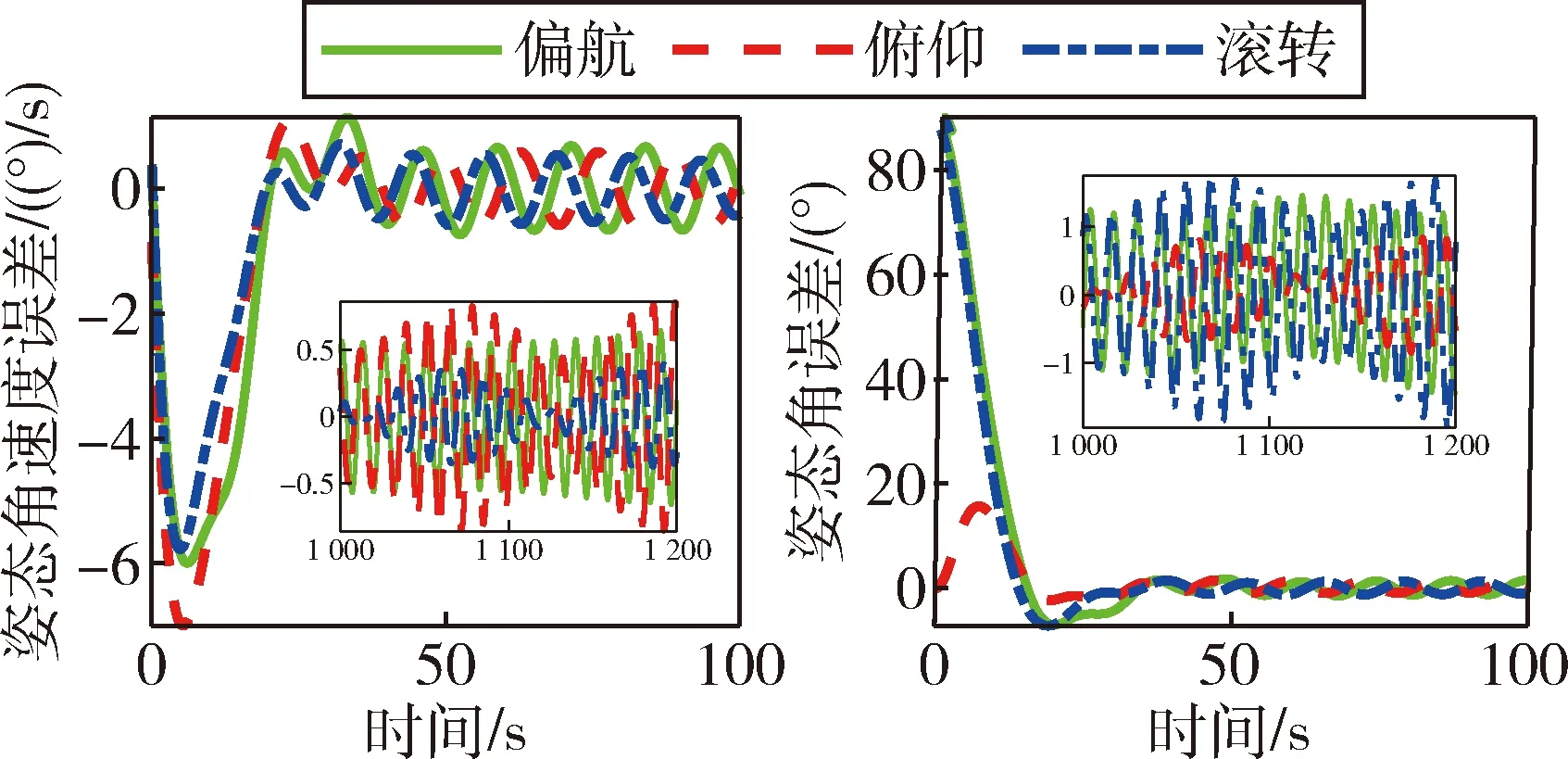
图5 控制律中转动惯量恒定时的控制误差Fig.5 The control errors with fixed inertia matrix in controller
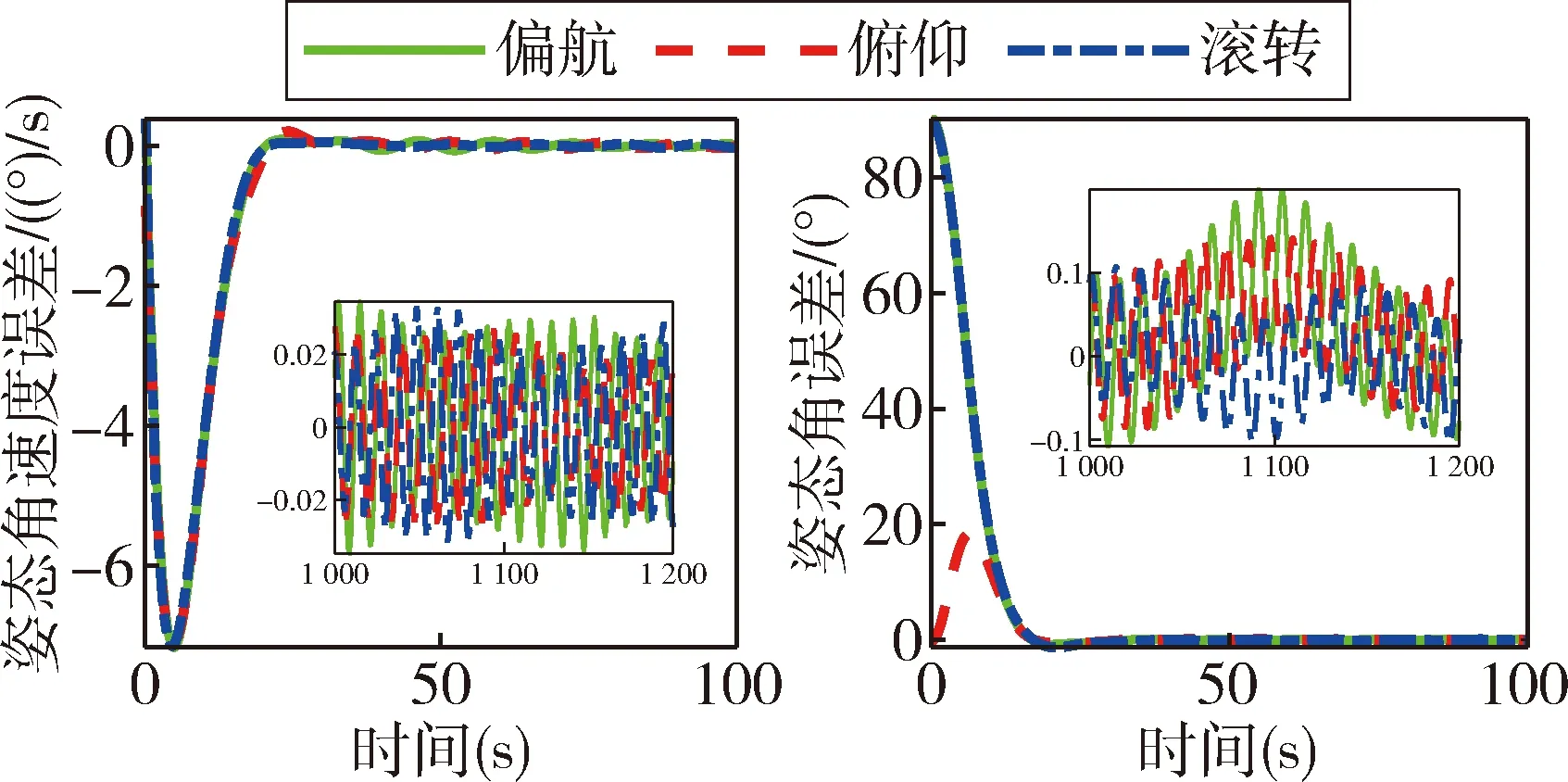
图6 控制律中转动惯量实时更新时的控制误差Fig.6 The control errors with updating inertia matrix in controller
5 结 论
本文对航天器时变转动惯量的辨识问题进行了研究.首先,设计航天器角加速度观测器.通过设计线性观测器并配置极点,实时观测航天器角加速度,用于转动惯量辨识.然后,设计时变转动惯量辨识算法.将参数变化过程引入了协方差矩阵,对扩展卡尔曼滤波进行了改进,结合航天器姿态动力学模型,实现了航天器时变转动惯量的辨识.将本文的方法与常规EKF算法和梯度下降法进行对比仿真和分析,本方法能够更加可靠地实现动态转动惯量辨识,辨识误差更小.最后,根据时变转动惯量的辨识结果,实时更新控制律中的参数信息,能够保证航天器姿态跟踪的控制精度.
