GEO在轨服务任务建模与强化学习服务序列规划
2022-08-01蔡亚星王兴龙朱阅訸
蔡亚星, 王兴龙, 朱阅訸
1. 国防科技大学 航天科学与工程学院,湖南 长沙 410073 2. 中国空间技术研究院 通信与导航卫星总体部,北京 100094
0 引 言
航天器在轨服务[1-3]是指在空间通过人、机器人或者两者协同完成涉及延长各种航天器寿命、提升执行任务能力的一类空间操作.地球同步轨道卫星经济价值高、工作寿命长、维修难度大,即使在增加了多种可靠性设计的前提下,依然有大量卫星发射后因为各种原因未能开展工作或出现寿命缩减.对于地球同步轨道卫星的许多故障,如太阳翼展开故障等,只需要施加很少量的在轨服务操作即可挽救卫星,获得显著的经济效益.在轨服务任务规划[4-6],即研究如何统筹安排服务资源,在最大化满足任务需求和资源充分利用的前提下,优化确定服务卫星的轨道机动、任务分配、服务序列等.单目标服务任务规划一般只涉及轨道设计问题,多目标服务任务规划通常还包括任务分配和服务序列规划问题.服务卫星需要合理规划目标间的转移轨道以及各目标的服务序列,获得速度增量和时间消耗最优的任务方案.
多目标服务任务规划问题已有不少研究.ZHOU等[7]提出了基于燃料补给站的“一对多”在轨加注任务规划方法,以速度增量和时间消耗为优化目标,将问题转化为多变量组合优化问题.欧阳琦等[8]将地球同步轨道“多对多”在轨加注任务规划视为旅行商问题,仅考虑异面变轨速度增量消耗,采用遗传算法进行求解.刘晓路等[9]建立了在轨服务资源分配和路径规划双层优化数学模型,并基于混沌遗传算法设计了在轨服务任务规划方法.强化学习作为一种任务决策算法,通过寻找最优动作的方式逐渐达到任务目标,能够在利用历史信息的同时保持较好的探索能力,近年来逐渐应用于在轨服务任务规划研究中[10-11].杨家男等[12]提出了基于启发强化学习的大规模主动碎片移除任务优化方法,采用改进蒙特卡罗树算法求解收益模型,获得了较优的规划结果.刘冰雁等[13]针对在轨服务资源分配问题,设计了基于改进深度Q网络的非线性多目标优化方法,在满足预期成功率的前提下优先分配重要服务对象,兼顾了分配效益与总体能耗.
现有的多目标服务任务规划研究大多仅针对服务卫星与目标卫星的交会过程计算速度增量和时间消耗,并未考虑交会对接后服务卫星执行服务任务过程中的速度增量和时间消耗.实际上,地球同步轨道卫星存在在轨加注、辅助位保、失效救援等多种服务任务需求,不同服务任务所消耗的速度增量和时间相差较大.同时,服务卫星在执行服务任务过程中,其轨道参数可能发生较大改变,直接影响与下一目标的交会轨迹规划.因此,多目标服务任务规划需针对不同目标的不同服务任务分别进行建模,全面考虑目标交会和任务执行过程中的轨道参数改变以及速度增量和时间消耗,规划得到最优的目标卫星服务序列.
本文提出一种地球同步轨道在轨服务任务建模与强化学习服务序列规划方法.推导霍曼-兰伯特四脉冲交会模型,针对不同服务需求建立在轨服务任务模型,基于强化学习规划得到目标卫星最优服务序列.最后通过仿真,验证任务规划方法的有效性.
1 地球同步轨道动力学建模
1.1 航天器轨道动力学模型
地球同步轨道多目标服务任务规划场景包含一颗服务卫星和多颗目标卫星,如图1所示.服务卫星和目标卫星均位于地球同步轨道带,不同目标卫星的服务需求不同,服务卫星需合理规划服务序列,依次完成对所有目标卫星的服务任务.为简化问题,服务卫星和目标卫星的轨道动力学模型均采用二体模型,不考虑轨道摄动影响,卫星位置和速度矢量均用其在惯性坐标系中的坐标分量表示.
服务卫星和目标卫星的轨道动力学方程为[14]
(1)
式中,rc/t、rc/t分别为服务卫星的轨道位置矢量和轨道半径,ac/t为服务卫星的控制加速度矢量,下标c/t分别表示目标交会过程/任务执行过程,ri、ri分别为编号为i的目标卫星的轨道位置矢量和轨道半径,μ为地球引力常数.

图1 地球同步轨道在轨服务任务场景Fig.1 On-orbit service mission scenario in geosynchronous earth orbit
1.2 霍曼-兰伯特四脉冲交会模型
航天器轨道交会问题是在轨服务任务规划的基本问题.霍曼(Hohmann)交会[15]是共面圆轨道间的最优轨道转移策略,所消耗的速度增量最小,但仅适用于初始轨道和目标轨道为共面圆轨道的情形.兰伯特(Lambert)交会[16]既适用于共面圆轨道也适用于异面椭圆轨道,因而广泛应用于非线性最优交会研究,但对于地球同步轨道远距离交会问题,单圈兰伯特方法得到的速度增量过大,多圈兰伯特方法计算量大,求解复杂,若嵌套在服务序列规划之中,优化交会序列的同时优化相邻两目标之间的交会轨迹,计算时间消耗将难以接受.
针对上述问题,本文采用霍曼-兰伯特四脉冲交会方法.如图2所示,服务卫星首先通过双脉冲霍曼转移,变轨至与初始轨道共面的某一中间轨道;然后利用地球同步轨道动力学特性,在中间轨道进行漂星;待漂至目标卫星附近时,再通过单圈双脉冲兰伯特方法完成与目标卫星的交会.

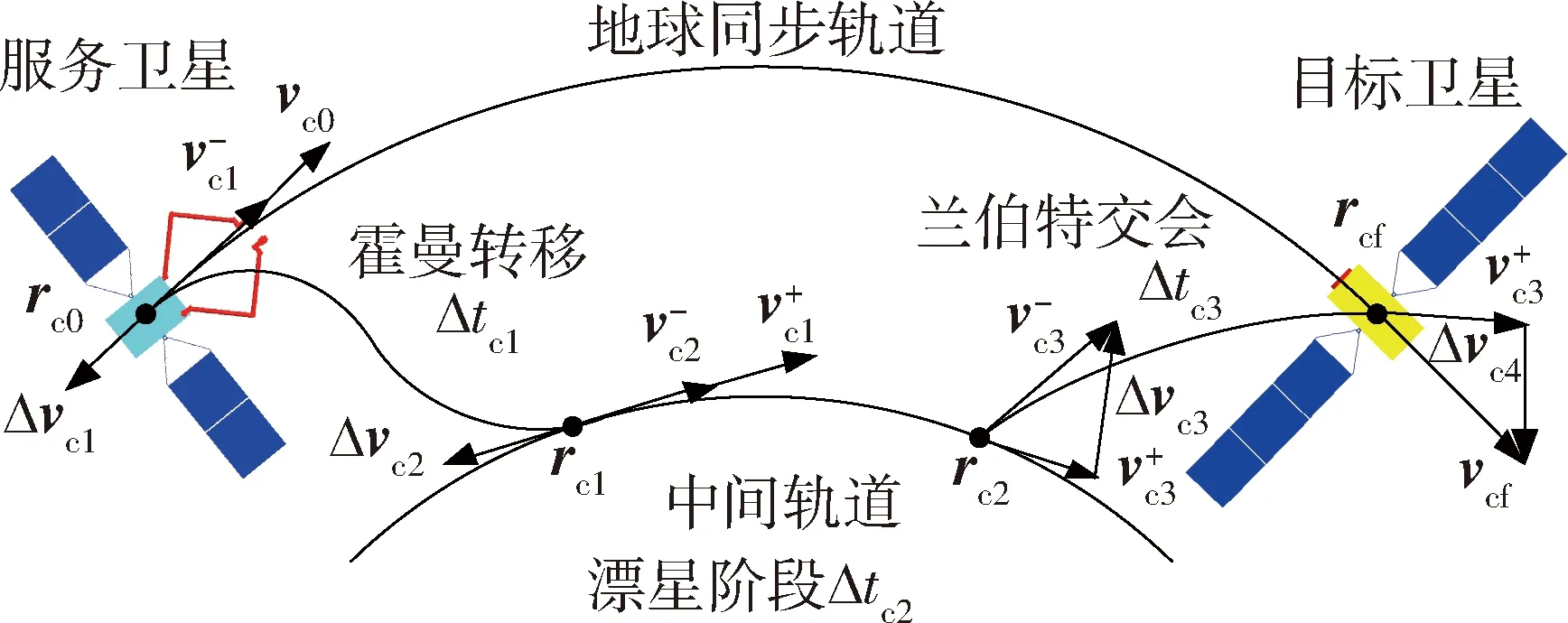
图2 霍曼-兰伯特四脉冲交会示意Fig.2 Illustration of Hohmann-Lambert four pulses rendezvous
(2)

霍曼转移时间Δtc1为
(3)
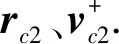
(4)
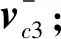
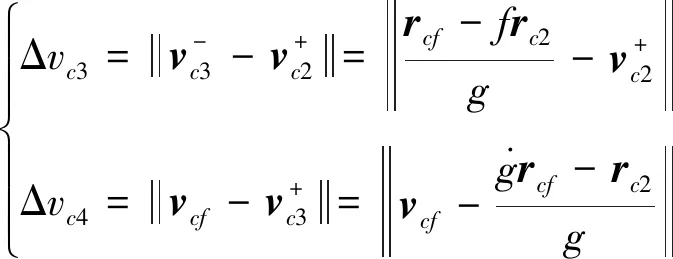
(5)
兰伯特交会时间Δtc3为
(6)
式中,f、g、Sz、Xz、Yz为单圈双脉冲兰伯特方法的中间变量[17].
服务卫星和目标卫星在交会点的位置和速度矢量rcf、vcf以及交会过程中各中间点的位置和速度矢量均可通过求解轨道动力学方程式(1)得到.
综上所述,霍曼-兰伯特四脉冲交会的总速度增量Δvc和交会时间Δtc分别为

(7)
2 地球同步轨道在轨服务任务建模
2.1 地球同步轨道服务需求分析
当前地球同步轨道卫星存在广泛且多样的在轨服务需求,如2009年美国GeoEye-1卫星天线指向系统发生故障,严重影响卫星正常业务开展;2013年俄罗斯AMOS-5卫星电源系统发生故障,影响发动机控制能力,造成卫星寿命缩短;2017年美国EchoStar-3卫星通信功能中断,卫星失效无法离轨,滞留于同步轨道缓慢漂移,多次与其它正常卫星产生碰撞风险.本文在统计分析地球同步轨道卫星在轨服务需求的基础上,归纳总结了5种典型的在轨服务任务,如表1所示.下文将分别对每种任务进行建模,根据服务卫星和目标卫星组合体在交会点的位置和速度矢量rt0=rcf、vt0=vcf,计算其在任务结束时的位置和速度矢量rtf、vtf,以及在任务执行过程中消耗的速度增量和时间Δvt、Δtt.
2.2 在轨加注/维修任务建模
对于在轨加注/维修任务,服务卫星与目标卫星交会对接后,一般就地在原轨道进行加注或维修,无需变轨,速度增量Δvt可视为零,任务时间Δtt取决于任务执行情况,一般为几小时到几天
(8)
将rt0、vt0、Δvt、Δtt代入式(1)求解可得任务执行结束时的位置和速度矢量rtf、vtf.

表1 典型地球同步轨道在轨服务任务Tab.1 Typical on-orbit service missions in geosynchronous earth orbit
2.3 辅助位置保持任务建模
对于辅助位置保持任务,服务卫星与目标卫星交会对接后,通过接管控制方式进行东西/南北位置保持.速度增量Δvt取决于轨道摄动大小,每年消耗量约44~52 m/s,任务时间Δtt根据任务要求而定,一般为几个月到几年:
(9)
将rt0、vt0、Δvt、Δtt代入式(1)求解可得任务执行结束时的位置和速度矢量rtf、vtf.
2.4 倾角漂移调整任务建模
对于倾角漂移调整任务,服务卫星与目标卫星交会对接后,在原轨道升/降交点进行变轨,将倾角调整至指定值,其它轨道参数不变.倾角漂移调整任务示意如图3所示.

图3 倾角调整任务示意Fig.3 Illustration of inclination adjustment mission
组合体在交会点的倾角和纬度幅角初值分别为it0、ut0,在升/降交点进行变轨,忽略发动机点火所用时间,任务时间Δtt即为组合体从交会点到升/降交点所用时间:
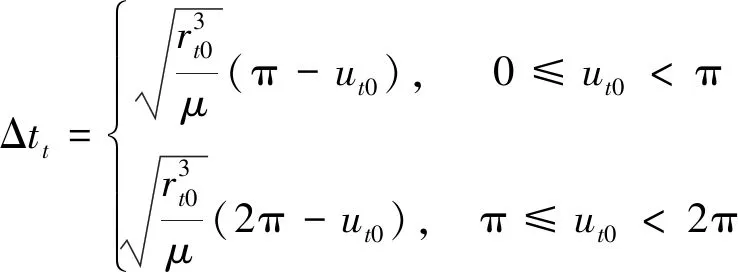
(10)
式中,rt0为组合体的轨道半径.
组合体在升/降交点的位置和速度矢量rtf、vtf可通过求解式(1)得到,倾角目标值itf根据任务要求设定,倾角调整前后速度大小vtf保持不变,则速度增量Δvt为
(11)
2.5 废弃卫星离轨任务建模
对于废弃卫星离轨任务,服务卫星与目标卫星交会对接后,将目标卫星轨道高度抬高至坟墓轨道.采用共面霍曼转移方法实现废弃卫星离轨,两次速度脉冲大小Δvt1、Δvt2分别为
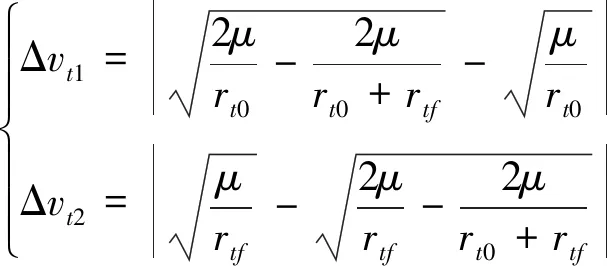
(12)
式中,rt0、rtf分别为交会轨道和坟墓轨道半径.
总速度增量Δvt和任务时间Δtt分别为
(13)
组合体在离轨点的位置和速度矢量rtf、vtf可通过求解式(1)得到.
2.6 失效卫星救援任务建模
对于失效卫星救援任务,服务卫星与目标卫星交会对接后,对其进行故障修复,然后再将其返回原轨道位置或转移到新轨道位置.考虑到失效目标卫星一般处于摄动漂移状态,倾角一般不为零,可采用异面四脉冲转移方法.
组合体在交会点的倾角初值为it0,倾角目标值itf=0.首先采用共面霍曼转移方法将组合体从交会轨道转移至中间漂星轨道,中间轨道半径rtm根据任务要求设定,两次速度脉冲大小Δvt1、Δvt2和转移时间Δtt1计算方法同式(12)~(13).然后利用地球同步轨道动力学特性,组合体在中间轨道进行漂星,漂星时间Δtt2根据任务要求设定.待漂至目标轨位附近时,再通过异面霍曼转移方法将组合体转移至目标轨位.异面霍曼转移示意如图4所示,同样采用双脉冲转移方法,在中间点施加第三次速度脉冲Δvt3,在改变轨道半径同时将倾角减小Δit;在入轨点施加第四次速度脉冲Δvt4,在轨道圆化同时将倾角减为零.

图4 异面霍曼转移示意Fig.4 Illustration of nonplanar Hohmann transfer
根据异面霍曼转移方法,两次速度脉冲大小Δvt3、Δvt4分别为
(14)

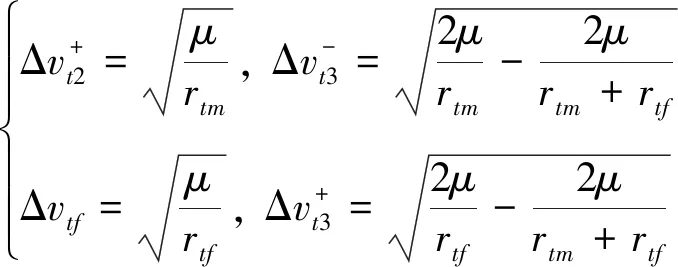
(15)
式中,rtf为目标轨道半径.
为使Δvt3+ Δvt4最小,需要满足条件
(16)
将式(14)~(15)代入式(16),求解得到Δit,从而得到最优速度增量Δvt3、Δvt4.转移时间Δtt3计算方法同式(13).
总速度增量Δvt和任务时间Δtt分别为

(17)
3 基于强化学习的服务序列规划
3.1 强化学习算法
强化学习是机器学习中的一个重要研究领域,采用试错机制与环境交互,通过最大化累积奖赏来学习最优策略.强化学习智能体在当前状态Sk下根据策略Π选择动作Ak,环境接收动作并转移到下一状态Sk+1,智能体接收环境反馈回来的奖赏Rk并根据策略选择下一步动作.目前常用的强化学习算法包括蒙特卡罗法、Q学习、SARSA 学习和策略梯度等[12].
Q学习是强化学习最重要的算法之一,主要思路是定义状态动作值函数(Q函数),并利用在线观测到的数据对Q函数进行迭代更新,更新公式为
Qj(Sk,Ak)=Qj-1(Sk,Ak)+αΔk
(18)
(19)
式中,α为学习率,Δk为时间差分误差,γ为折扣因子,下标j-1、j分别表示上次学习和当前学习过程,下标k、k+1分别表示当前时刻和下一时刻.
Q学习在训练过程中通常采用ε贪心策略或Softmax策略来平衡探索与利用的关系.训练完成后,最优策略Π*可根据式(20)得到
(20)
3.2 状态与动作定义
假设本文研究的地球同步轨道在轨服务任务场景共包含n颗目标卫星,编号分别为1~n.服务卫星在进行服务序列规划时,需要明确当前状态下哪些目标卫星已服务,哪些目标卫星尚未服务,以及正在服务哪颗目标卫星.因此,当前时刻k的状态Sk定义为
Sk=[sk1sk2…skn]
(21)
式中,ski表示目标卫星i在当前时刻k的服务状态

(22)
当前状态Sk下,服务卫星进行任务规划,在尚未服务的目标卫星中选择一颗作为下一服务对象.因此,当前时刻k的动作Ak定义为所选择作为下一服务对象的目标卫星编号
Ak∈{i∈Z+|1≤i≤n,ski=-1}
(23)
服务卫星执行动作Ak后,环境接收该动作并转移到下一时刻k+1的状态Sk+1,状态转移方程为
Sk+1=[s(k+1)1s(k+1)2…s(k+1)n]
(24)
式中,s(k+1)i表示目标卫星i在下一时刻k+1的服务状态
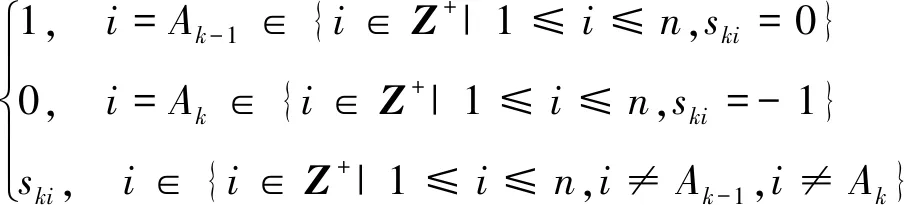
(25)
3.3 奖赏函数定义
服务卫星在当前状态Sk下执行动作Ak,以目标卫星Ak为下一服务对象,采用本文建模方法可以得到目标交会过程消耗的速度增量和时间Δvc、Δtc,以及任务执行过程消耗的速度增量和时间Δvt、Δtt.以对目标卫星Ak服务全过程的速度增量和时间消耗最小化为目标,则服务卫星在当前状态Sk下执行动作Ak获得的奖赏Rk定义为目标交会过程和任务执行过程消耗的速度增量和时间的加权和:
Rk=-η1(Δvc+Δvt)-η2(Δtc+Δtt)
(26)
式中,η1、η2分别为速度增量和时间对应的权重系数.
3.4 服务序列规划流程
根据上述建模,基于强化学习的服务序列规划流程如下:
1)设定学习率α、折扣因子γ、贪心率ε、最大学习次数jmax,初始化状态动作值函数Qj(S,A),j∈Z+,1 ≤j≤jmax;
2)对于每次学习过程j,初始化状态Sk,k∈Z+,1≤k≤n,设定状态初值S1=[-1 -1 … -1];
3)对于每一时刻k,服务卫星感知当前时刻k的状态Sk,采用ε贪心策略根据式(23)选择动作Ak;
4)服务卫星执行动作Ak,计算得到对目标卫星Ak服务全过程的速度增量Δvc、Δvt和时间Δtc、Δtt,根据式(26)计算得到奖赏Rk,根据式(24)~(25)计算得到下一时刻k+1的状态Sk+1;
5)根据式(18)~(19)更新状态动作值函数Qj(Sk,Ak),作为下次学习采用ε贪心策略选择动作的依据;
6)判断是否k=n,若是,计算累积奖赏R=R1+R2+…+Rn,转7);若否,置k=k+1,转3);
7)判断是否j=jmax,若是,表明学习过程完成,转8);若否,置j=j+1,转2);
8)根据式(20)生成最优策略Π*,得到服务卫星对目标卫星的最优服务序列.
4 仿真验证
4.1 工程算例
通过工程算例进行仿真,验证本文任务规划方法的有效性.根据北美防空司令部(NORAD)发布的TLE两行轨道根数,从中随机选取10颗地球同步轨道卫星作为目标卫星进行在轨服务任务规划.服务卫星和目标卫星的初始轨道参数分别如表2和表3所示,目标卫星的服务需求和量化参数如表4所示.强化学习算法的学习率α=0.1,折扣因子γ=1.0,贪心率ε采用递减策略,初值εini=0.9,末值εend=0.1,最大学习次数jmax= 1000.

表2 服务卫星初始轨道参数Tab.2 Initial orbit parameters of service satellite

表3 目标卫星初始轨道参数Tab.3 Initial orbit parameters of target satellites

表4 目标卫星在轨服务需求Tab.4 On-orbit service requirements of target satellites
4.2 仿真结果
基于强化学习算法进行目标卫星服务序列规划仿真.为增加对比,针对同一算例分别进行两种工况仿真.工况1计算单步奖赏Rk时仅考虑目标交会过程消耗的速度增量和时间Δvc、Δtc,工况2计算单步奖赏Rk时全面考虑目标交会和任务执行过程消耗的速度增量和时间Δvc、Δtc、Δvt、Δtt.两种工况仿真得到的强化学习过程累积奖赏分别如图5~6所示,图中蓝线表示每次学习过程的累积奖赏,红线表示最近20次学习过程的平均累积奖赏.工况1最终学习得到的目标卫星服务序列为4→3→1→9→10→7→6→2→8→5,工况2最终学习得到的目标卫星服务序列为4→3→1→9→6→7→5→8→2→10.基于两种工况得到的服务序列,计算服务卫星速度增量Δv随时间Δt变化情况,结果分别如图7~8所示.图中,实心红点表示服务卫星与目标卫星交会时的参数,红色数字表示目标卫星编号;空心蓝点表示服务卫星和目标卫星组合体任务执行完成时的参数.

图5 强化学习过程累积奖赏(工况1)Fig.5 Cumulative reward in reinforcement learning process (Case 1)
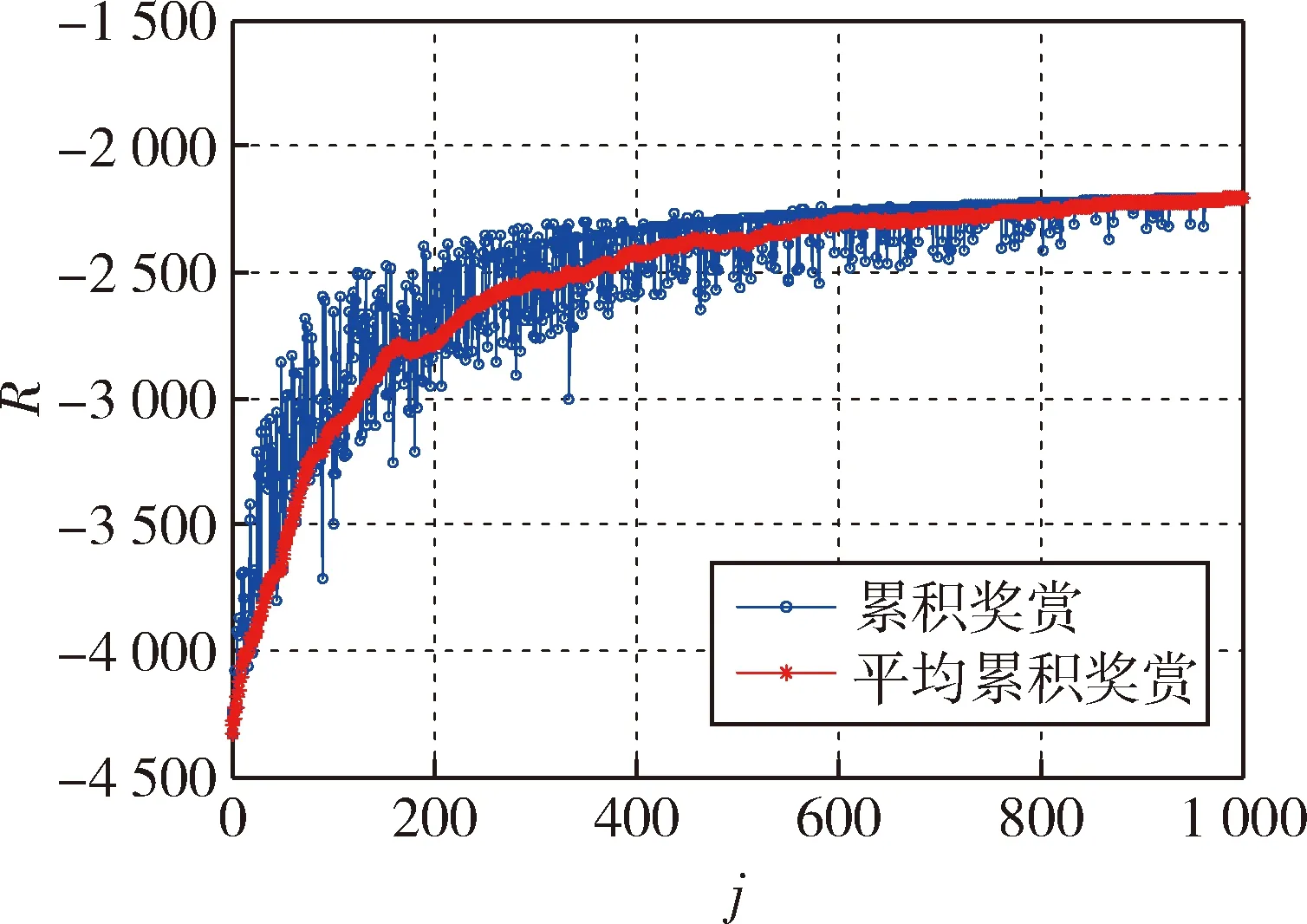
图6 强化学习过程累积奖赏(工况2)Fig.6 Cumulative reward in reinforcement learning process (Case 2)
根据单步奖赏Rk定义,速度增量和时间消耗越小,累积奖赏越大.从图5~8中可以看出,工况1由于未考虑任务执行过程,累积奖赏、速度增量和时间消耗均大于工况2,与实际情况不符.表明工况1未能真实反映实际在轨服务任务过程,规划得到的服务序列不是最优服务序列.而工况2全面考虑目标交会和任务执行过程,规划得到的服务序列明显优于工况1规划结果.
根据工况2规划得到的最优服务序列,极坐标形式的服务卫星倾角i和升交点赤经Ω变化如图9所示.服务卫星倾角i、升交点赤经Ω、半长轴a随时间Δt变化分别如图10~12所示.从图9~12可以看出,最优服务序列规划结果能够全面反映服务卫星在目标交会和任务执行过程中的轨道参数改变.其中目标卫星5、6需要进行倾角漂移调整,目标卫星9、10需要进行失效卫星救援,任务执行过程中i、Ω存在较大改变;目标卫星7、8需要进行废弃卫星离轨,任务执行过程中a存在较大改变,符合在轨服务需求.

图7 服务卫星速度增量和时间消耗(工况1)Fig.7 Velocity increment and time consumption of service satellite (Case 1)

图8 服务卫星速度增量和时间消耗(工况2)Fig.8 Velocity increment and time consumption of service satellite (Case 2)

图9 服务卫星倾角和升交点赤经(工况2)Fig.9 Inclination and right ascension of ascending node of service satellite (Case 2)

图10 服务卫星倾角(工况2)Fig.10 Inclination of service satellite (Case 2)
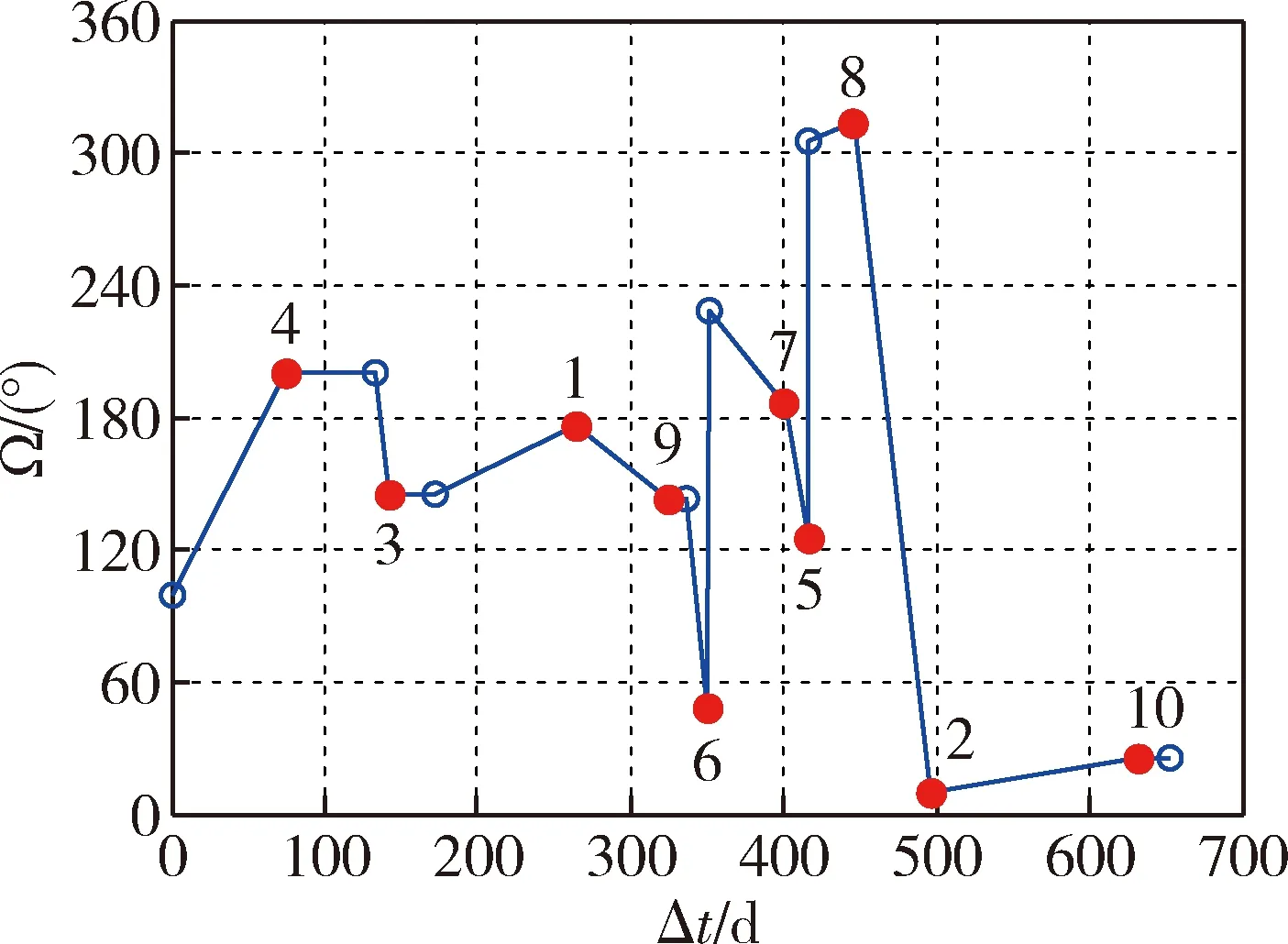
图11 服务卫星升交点赤经(工况2)Fig.11 Right ascension of ascending node of service satellite (Case 2)

图12 服务卫星半长轴(工况2)Fig.12 Semi-major axis of service satellite (Case 2)
5 结 论
本文针对地球同步轨道在轨服务任务规划问题,设计了霍曼-兰伯特四脉冲交会方法,根据不同类型服务任务建模提出了基于强化学习的服务序列规划方法,并通过数值仿真验证了方法的有效性和适用性.仿真结果表明,霍曼-兰伯特四脉冲交会模型能够有效解决地球同步轨道远距离交会速度增量过大问题,计算量小,便于应用;基于强化学习的服务序列规划方法能够全面反映服务卫星在目标交会和任务执行过程中的轨道参数改变以及速度增量和时间消耗,所得目标卫星最优服务序列更加真实有效.
实际工程应用时,可先期在地面进行强化学习离线训练,将训练得到的状态动作值函数表上注卫星作为初始策略依据,再通过迁移学习等方式进行在轨适应性调整,以获得较好的任务泛化能力.
