主动冷却结构的拓扑优化设计及流动传热分析*
2022-08-01段治健马欣荣
段治健 马欣荣
(1.咸阳师范学院数学与统计学院 咸阳 712000)(2.西北工业大学机电学院 西安 710072)
1 引言
流体流动系统和传热装置广泛应用于电子设备、热交换器网络、汽车工业、发动机、发电机、航天飞机、潜艇、火箭和卫星设计中。尤其是发动机、电子芯片散热设计中冷却流道设计不当会导致零件严重过热,从而限制使用性能和耐久性,甚至导致结构损坏。因此,为了获得更好的性能和更低的成本,必须设计高效的冷却系统。
拓扑优化设计为此提供了新颖思路,该方法最早由Bensøe 和Kikuchi[1]建立并成功应用于固体力学问题的结构优化。优点在于:允许在优化过程中改变结构拓扑;最终设计几乎不依赖于初始设计。Gersborg-Hansen 等[2]首次将有限体积法应用于二维稳态热传导问题。Borvall 和Peterson[3]的工作开创了流体传热系统的拓扑优化设计研究。Yoon[4]首次在二维结构网格上,忽略流体区域内浮力和粘性耗散的影响,采用有限元方法研究了强迫对流温度场的共轭拓扑优化问题,并发现对流-热传导之间的平衡对传热系统中散热结构设计的影响较大。Sun等[5]提出了基于密度变量的三维热流冷却系统的大规模拓扑优化方法。Joo 等[6]为了研究自然对流中的形状依赖效应,考虑传热系数在计算域内变化,提出了一种新的替代模型,采用弱耦合拓扑优化方法对自然对流散热器进行了传热优化。Sato 等[7]以换热最优和压降最小为目标,提出了微通道热沉的基于水平集方法的拓扑优化策略。裴元帅等[8]采用变密度方法设计了风冷热沉结构。Haertel 和Nellis[9]将基于密度变量的拓扑优化方法应用于干冷式电厂冷凝器气侧表面的设计,建立了稳态热流耦合充分发展的内流拓扑优化模型。Koga 等[10]首次开展了拓扑优化微通道热沉的实验研究,验证了拓扑构型数值结果的正确性。文献[11~12]进一步进行了实验研究,验证了数值结果的有效性。Kontoleontos 等[13]将拓扑优化方法推广应用于S-A湍流模型对流传热问题。此外,针对不同流态、离散求解方法、伴随格式以及优化求解方法得到了广泛应用和研究[14~20]。

表1 对流传热拓扑优化方法对比
针对超燃冲压发动机冷却结构的简化模型,本文提出了流固耦合传热结构的拓扑优化方法。采用有理近似方法处理材料属性,结合移动渐近线方法,给出了约束条件下超燃冲压发动机冷却结构的最佳流道分布,为实际工程问题提供理论依据。
2 几何模型及边界条件
2.1 几何模型
超燃冲压发动机二维模型设计尺寸:长度为1m,宽度为1m,其中水力直径L 为0.2m,如图1(a)所示。设计域由流体与固体组成,给定设计区域材料初始密度为0.5。
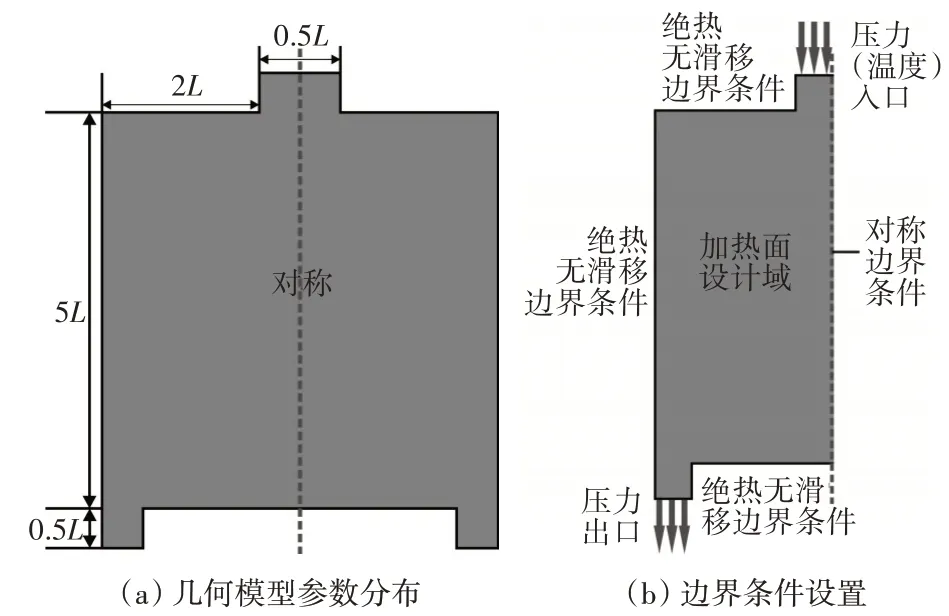
图1 超燃冲压发动机二维几何模型
2.2 边界条件
控制方程为连续方程、动量方程以及能量方程,基于非结构网格,采用间断Galerkin 有限元方法[21]离散求解偏微分方程组。为了简化计算,仅采用半模进行计算,对称边界条件设置如图1(b)所示,固体外表面采用绝热无滑移边界条件,材料设计区域施加恒定热源。设计域的初始温度为293.15 K,设计域中的流体与固体材料属性值如表2所示。
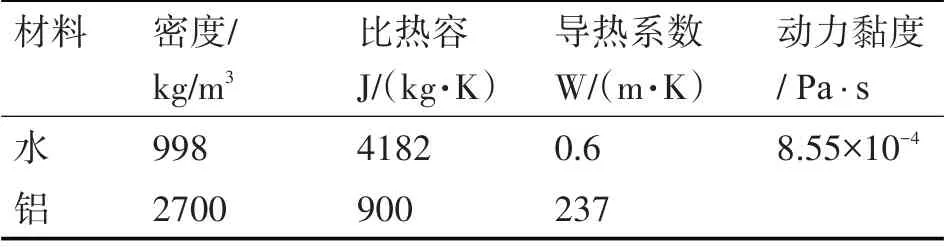
表2 流体、固体材料属性参数
3 拓扑优化方法
3.1 流动传热方程
忽略重力和浮升力的影响,基于Boussinesq 假设条件下的稳态不可压Navier-Stokes方程为
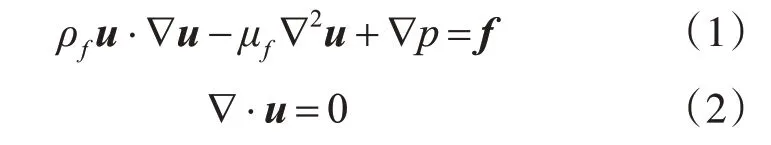
式中:ρf为流体密度;μf为流体动力黏度;u为流体速度;p为压力,f为源项。


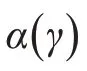

3.2 材料属性插值方法
优化结构的形状由材料分布决定,因此多孔材料属性采用有理近似插值方法(Rational Approximation of Material Properties,RAMP)[14]计算。构造材料的惩罚系数、热导率、密度及比热容为
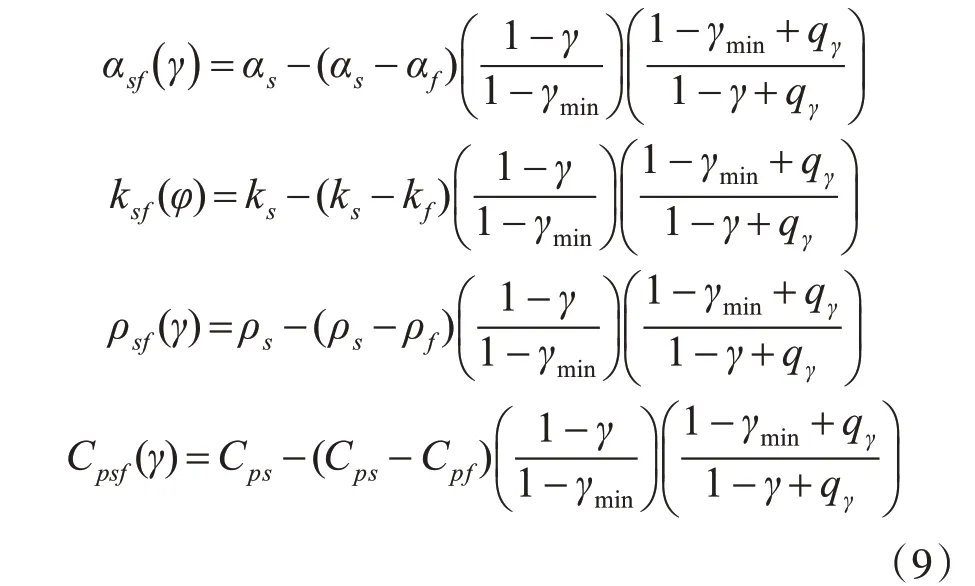
其中:αsf为惩罚系数,ρsf为材料密度,ksf为材料热传导系数,Cpsf为材料比热容,qγ=0.01。γ为设计变量,当γ=1 时,αsf=αs,代表固体区域;当γ=0时,αsf=αf,代表流体区域,因此拓扑优化问题转化为0-1规划问题。
3.3 灵敏度分析
流动传热耦合方程可以表达为残差形式:


与直接微分法基本一致,但计算效率明显提升。
3.4 拓扑优化模型
在设计区域中给定材料初始密度、体积约束,通过温度场控制流体物性参数,进而由流场影响温度场,实现双向耦合,从而构建对流传热双向耦合拓扑模型。
满足:
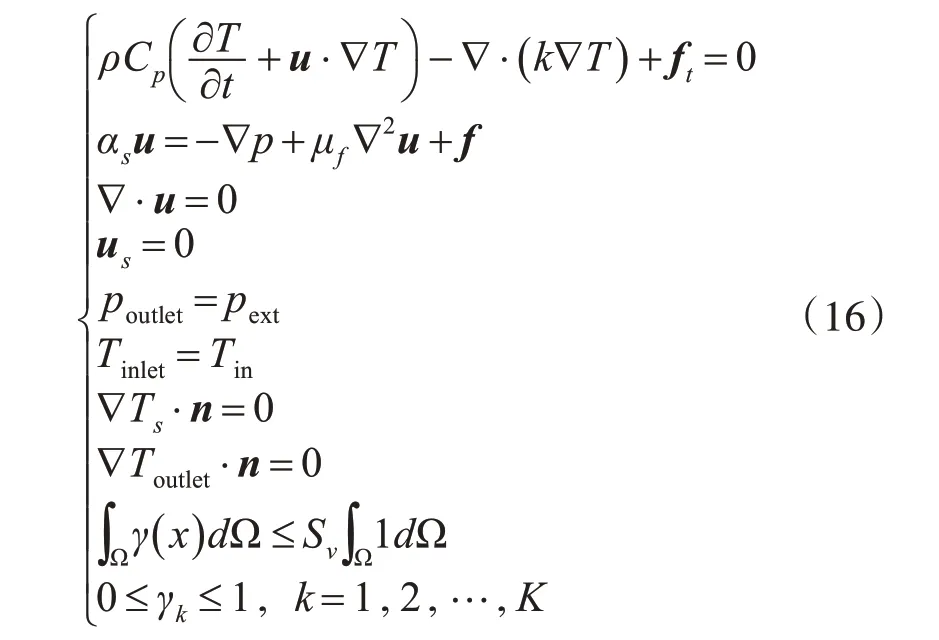
其中:γk为材料分布值,Sv=0.4为材料体积约束上限占比,采用GCMMA求解拓扑优化问题[22]。
4 计算结果与分析
4.1 算法验证
考虑流动问题[23]:3.5mm×5mm 的矩形设计区域,两入口对应两出口,进出口高度为1mm,长度为2mm,如图2所示。
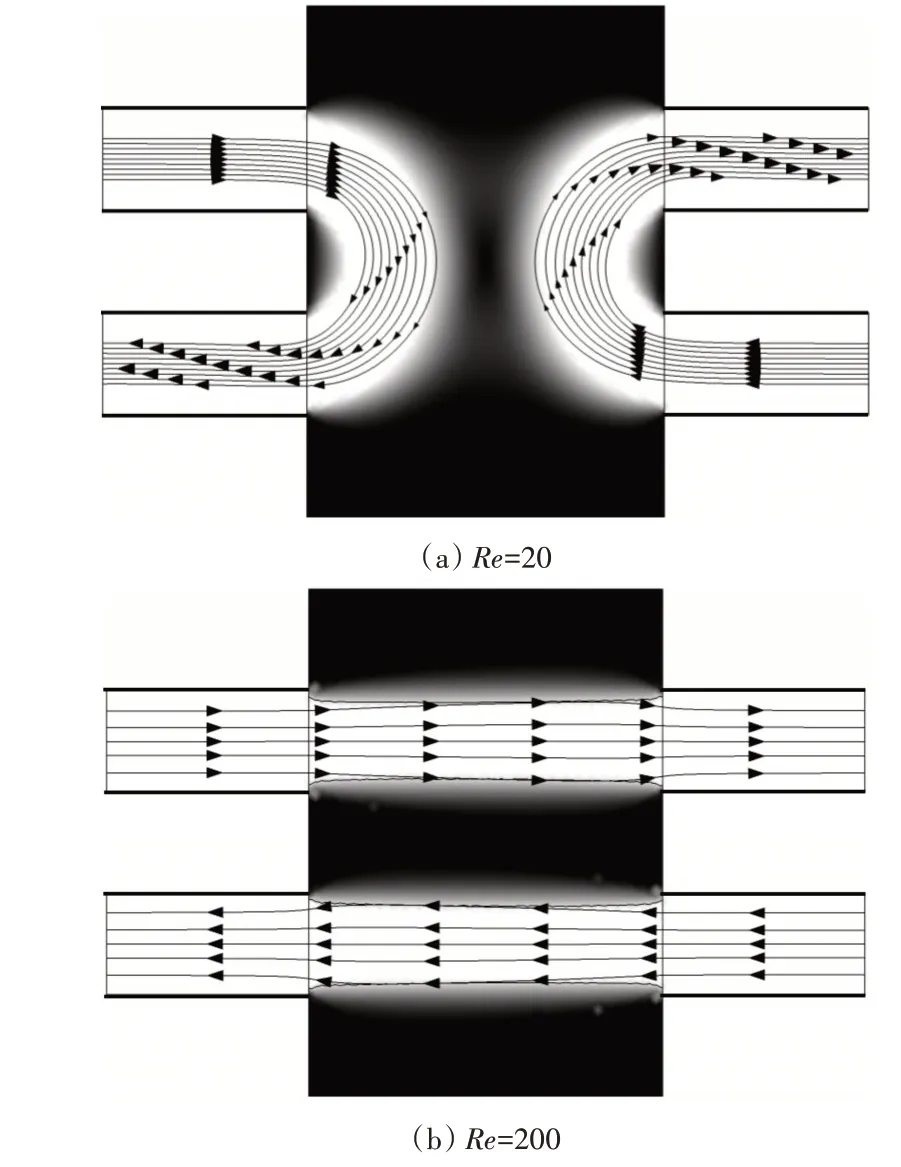
图2 不同雷诺数Re的材料与速度流线分布
图2(a)、(b)分别给出了Re 为20 与200 时,设计域最优材料与速度流线分布。低雷诺数下,为了减少功率损耗,流体通道应尽可能短且宽,因此在Re=20 时,形成了U 形通道;随着雷诺数增加,当Re=200 时,弯曲区域流体的功耗随之增加,当惯性占主导地位时,在弯道处存在较大的速度梯度,因此通道自然优化为两条平直通道。计算结果与文献[23]保持一致,验证了本文算法的可靠性与准确性。
4.2 优化结果对比
图3(a)显示了设计域中的初始温度分布;图3(b)给出了拓扑优化后的温度分布,其中流体占比为0.6。与超燃冲压发动机主动冷却系统的初始温度场相比,优化后的冷却结构温度明显降低,能量损失显著改善,且温度分布更加均匀,避免了高温集中区的发生。初始流场的最高温度与平均温度分别为325.74 K、313.18 K,拓扑结构的最高温度与平均温度分别为293.88 K、293.29 K,拓扑结构最高温度与平均温度分别降低了9.8%和6.35%。因此,计算结果表明拓扑优化结构具有良好的散热性能。
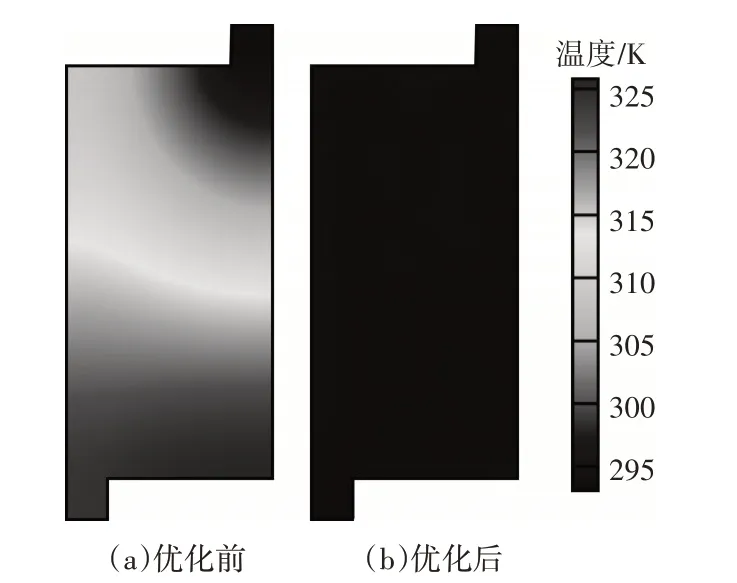
图3 拓扑优化前后温度分布
图4 给出了拓扑优化结构流线与流道材料分布,(a)为速度流线分布,(b)为流道结构材料分布。通过在设计域内施加均匀热源,实现超燃冲压发动机的底部加热效应。进出口压差为2 Pa,拓扑优化形成的通道结构包括:从进出口延伸的宽较的主通道,主通道内流速较高,相邻主通道之间形成多条细支通道,使冷却通道覆盖整个设计区域。
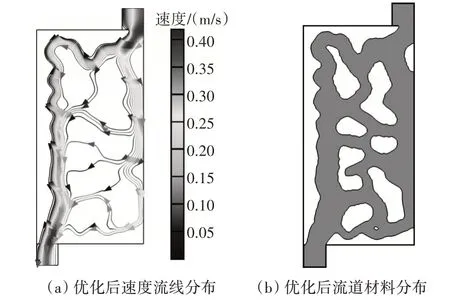
图4 拓扑优化速度流线与材料分布
由于入口与出口的压降固定,整个通道结构表现为主通道的宽度大于分支通道的宽度,减少了其他部分的流动损失,通道之间的宽度差较小,流速分布更均匀,在设计域内具有更好的冷却效果。
图5 给出了拓扑优化计算中不同迭代步数(n=0,10,50,100)的材料和速度流线分布。显然,随着迭代次数的增加,主通道中的速度逐渐增加,流线分支的数量逐渐增加。当迭代步数n>50 后,主流通道速度变化微小。流道结构逐渐清晰,最终优化后的结构边界轮廓清晰。拓扑优化结构明显降低了设计域内的平均温度,与工程实际情况相符。
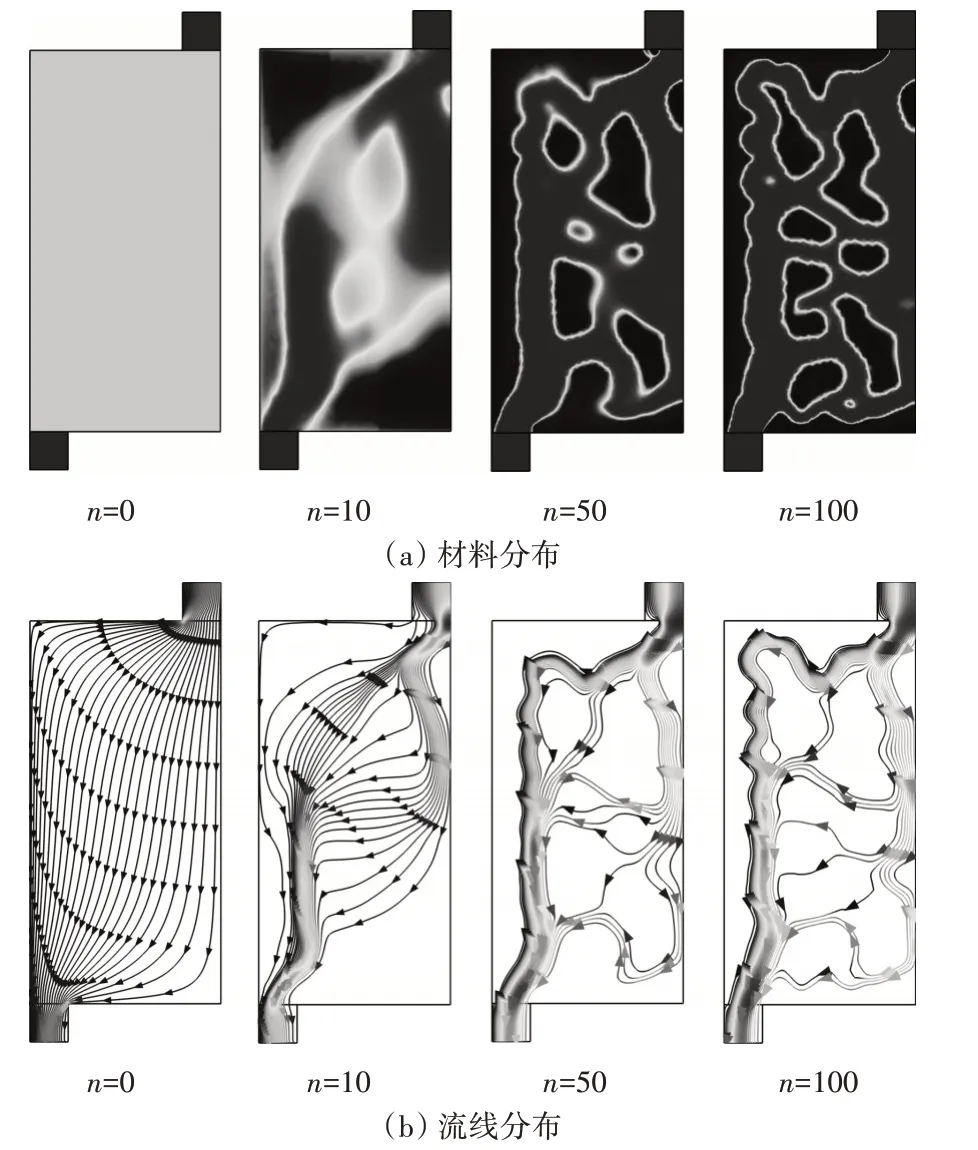
图5 不同迭代步的材料分布和流线分布
4.3 传热性能对比
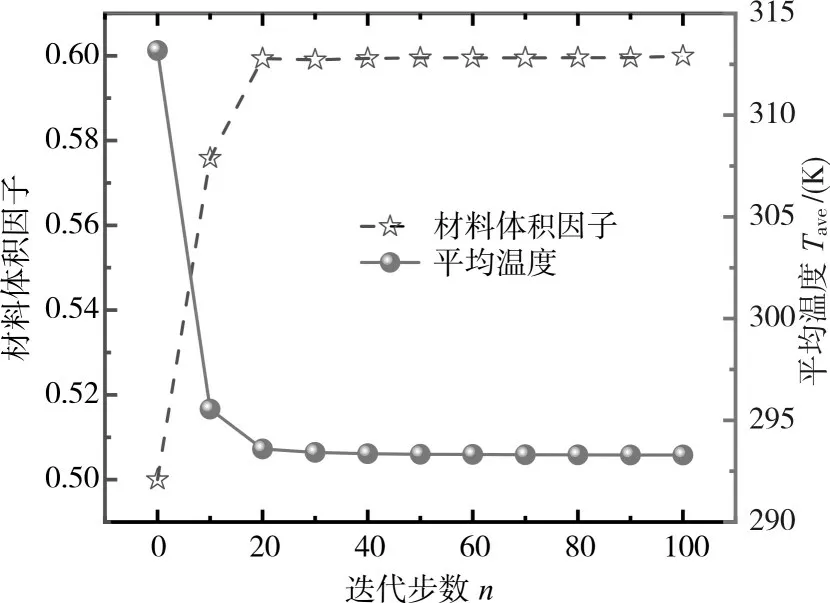
图6 拓扑优化模型收敛历史
5 结语
本文提出了一种超燃冲压发动机主动冷却系统的拓扑优化方法,并采用非结构网格间断有限元法对主动冷却系统的流动与传热特性进行了数值研究,得出以下结论:
1)结合GCMMA 和RAMP 插值方法,实现了主动冷却系统内部冷却通道的拓扑优化结构设计。通过经典算例验证了算法的可靠性,与初始设计域相比,拓扑结构温度明显降低,分布更加均匀。
2)随着拓扑优化迭代次数的增加,拓扑结构呈现为主支和分支的混合结构且分支逐渐增多,流道边界轮廓逐渐清晰。拓扑优化方法具有良好的收敛性,有效降低了设计区域的平均温度,符合工程实际需求。
