基于ARIMA-小波分析的加拿大气温时空变化趋势研究*

肖 旋 杨新凯

（上海师范大学信息与机电工程学院 上海 201418）

1 引言

IPCC 第五次气候评估得出结论为1880 年～2012年地表均温呈现上升趋势，涨幅大约0.85℃［1］。很多科学家持有观点是地球变暖可能致使更多的极端天气事件的发生。季飞、吴召华使用最新开发的非线性趋势检测方法-多维集合经验模式分解来评估了全球陆地表面气温［2］。朴世龙与团队使用北半球高纬度区域大气CO2含量观测数据、遥感数据、大陆生态系统和海域碳往复运动变化模型，并联合大气输导，系统分析了1980年～2010年北半球高纬度地域生态系统春季碳汇因气温变化相应的动态改变及其机制［3］。探索温度时空演变规律，对未来地区气候预测、保护和改善自然环境及地区的可持续发展提供科学支撑。

针对气候变化的数据：1）根据年代际的距平变化和ARIMA 时间序列分析的综合结果可以得出，从1940 年～2010 年加拿大温度的时间变化趋势为升高、降低、升高的趋势。2）选取ArcGIS 绘图软件，通过反距离权重插值法在地图上绘制温度的空间分布得出东西海岸平均温度上涨了大约2℃左右，内陆地区大部分上升幅度都大于了4℃，北极三省的上涨幅度较大，基本都大于了6℃。特别北极圈内，涨幅超过了10℃。3）通过小波变换分析得出1980 年～2010 年地球海洋表面气温的改变趋向为变暖趋势。大约10 年为一个全球海表温度的变化周期，一个较强的扰动出现在约5 年～6 年的尺度上。

2 数据来源

加拿大划分为十个省和三个特别行政区，本文所用的加拿大各地天气的历史数据均来自加拿大气象网站，预处理的数据是温度、降雨量、降雪量等403 个气象站点1940 年～2010 年月值数据，具体气象站点如图1 所示，落在研究区域的这些气候数据符合均匀分布、完整性、典型性的可用性数据特征。

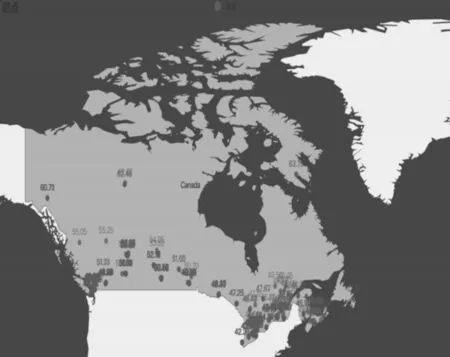
图1 气象站点分布

对加拿大403 个站点1940 年～2010 年各气象资料进行处理加工，得到月平均值及年平均值。

3 数据准备

首先将下载的数据采用Python 的pandas 进行数据清洗，主要包括以下流程。

3.1 缺失值处理

在进行问题探究和收集数据中发现，数据集中数值缺失较多。经过数据库检测发现多数的变量都或多或少的缺失，而这些数据的缺失对加拿大的气象站点的数据分析有较大的影响，所以这一部分的处理是非常重要的，不可忽视。对于这种缺失数据值，我们决定采用数据补齐的方式，首先可以先根据其他的相关字段进行预估，比如地区的变量等等。若上述方法无法实现填充，缺失的样本值则通过相关性寻找最近距离的K个样本值，再将其加权平均的结果值来补全数据［4］。

3.2 数据标准化

在处理数据前，通常需要规范化数据。因为一般在多指标评价机制中，每一个指标它的衡量性质并不完全相同，数量级和量纲一般有差异。若是这些指标之间的情况相差非常小，影响会较小；但如果这些指标之间相差水平很大，一般来说会增大数值大的指标在整体分析中的影响，而数值小的指标相对应的影响就会被减弱。本文在进行数据标准化的时候，主要采用了min-max 标准化，通常也将之称为规范化方法，下面对其进行详细介绍。

对序列x1,x2,x3,···,xn进行变换：

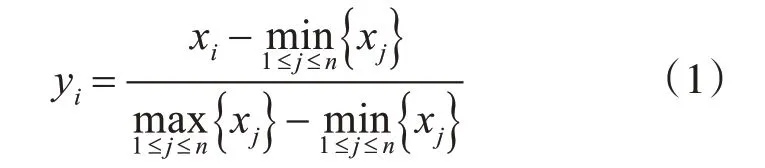
3.3 数据初步展示

经过数据预处理后，我们先用雷达图简单的呈现全部数据的整体走向趋势的概况，预先了解温度的大体变化走向，我们将数据的csv 文件导入python 程序，经数据统计，用雷达图逐年代展示温度变化趋向。

如图2 所示越往里温度值越低，越往外温度值越高，每年温度12 个月份的变化趋势，6 月～9 月温度全年最高，12 月～2 月温度全年最低。1940 年～2010年每月温度的变化趋势基本一致。

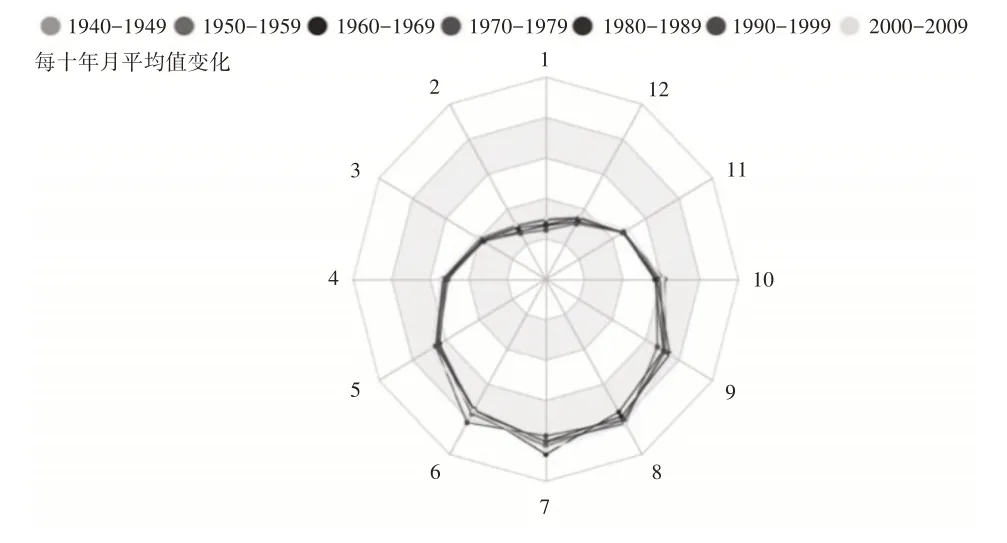
图2 温度变化雷达图

4 研究方法

4.1 线性趋势估计

本文运用的主要是根据魏凤英老师的《现代气候统计诊断与预测技术》一书中推荐的线性趋势评估法，线性趋势估计法是用一条合理的直线指示天气变量与时间变量的联系。［5］用xi表示样本量为n的某一气象变化值，用ti表示xi所对应的时间，构建xi与ti之间的一元线性回归方程：

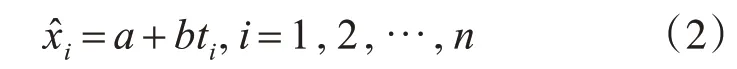
其中，a为回归常数，b为回归系数，a和b可用最小二乘法进行估量［5］。

对于观测数据xi及相应的时间ti，回归常数a和系数b的最小二乘法估值为

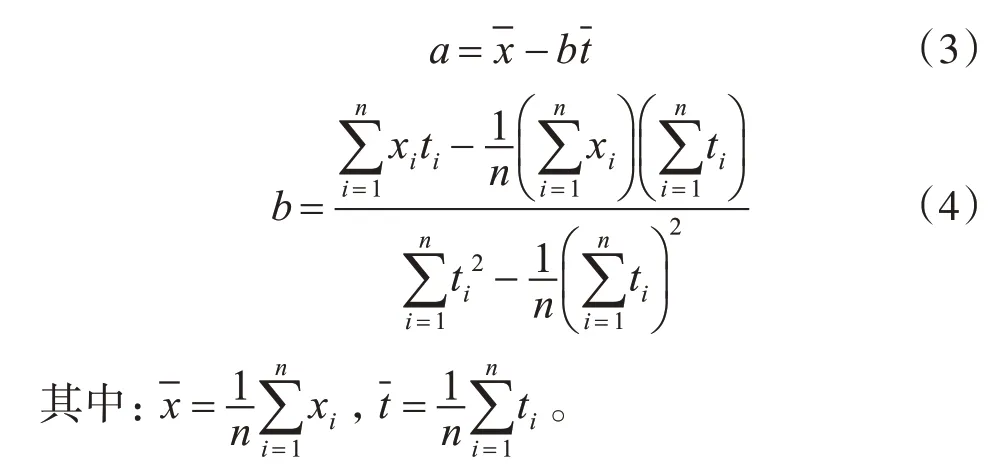
时间ti与变量xi之间的相关系数借助回归系数b与相关系数的关联性计算：

4.2 相关分析与回归分析

4.3 移动平均

移动（滑动）平均可用来模拟趋势，在训练量为n时，给定时间序列x，此处为气候变化序列x，取其平均值描绘分析波动趋势［5］，表达其滑动平均序列是：

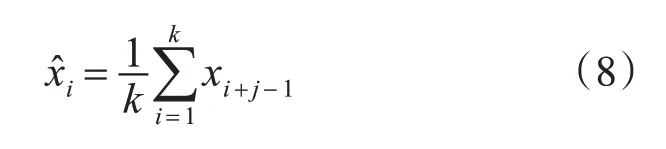
式（8）中，滑动长度为k，j=1,2,…,n-k+1。观察七十年的时间序列以及分析周期，将滑动窗口k设置为10，即观测气候序列的变化趋势是通过10年一个滑动分离出变化趋势以探究规律。

4.4 ARIMA时间序列分析

ARIMA 模型（Autoregressive Integrated Moving Average model），也就是所谓的差分整合移动平均自回归模型（移动也可称作滑动），预测时间序列的趋势［10］。ARIMA（p，d，q）里，p 是自回归项数，用来解释时间序列模型中数据自身的滞后数，即AR项，d 是要达到平稳序列需要做的差分次数，即Integrated 项，q 是滑动平均项数，表示该模型在预测误差范围内产生的滞后数，也就是MA 项［10］。“差分”是关键步骤。

此模型被选择来预测温度随时间推移的变化序列。由ARMA（p，q）模型的延伸扩充获得ARIMA（p，d，q）模型。ARIMA（p，d，q）模型表达式是：

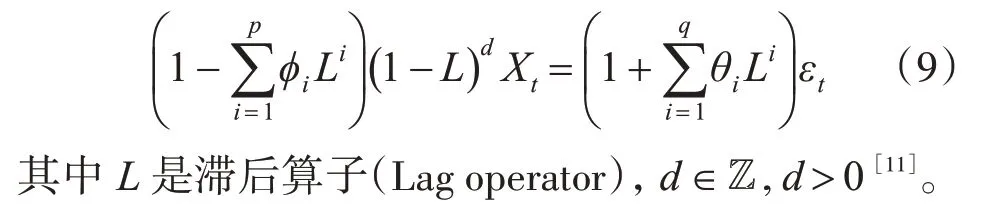
4.5 小波分析

1）小波概念

小波分析来自于Fourier，并且实现了Fourier所不能实现的一些艰难问题，适合于处理非稳定信号［12］。小波分析可以用于时间-尺度分析和多分辨率分析。其波形同时具有衰减性和波动性，定义公式如下：

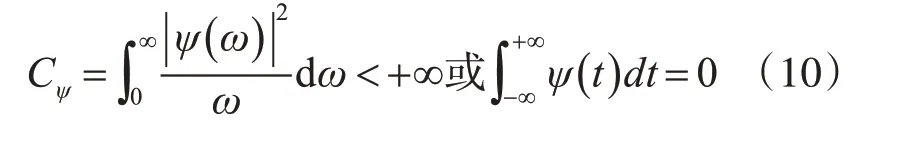
2）小波变换

小波变换是将函数和数据等切分成不同的片段，然后分析相应的尺度分量，小波变换有两种变换方式，一种是通过连续形式实现变换，另一种则是采用离散手段达到变换；其中，离散小波又有着多种不同形式，比如：正交、双正交小波。［13］由于海表温度的数据有一定的连续震荡的特征，所以采用一维连续小波变换分析其变化特点。一维连续小波变化的公式如下：

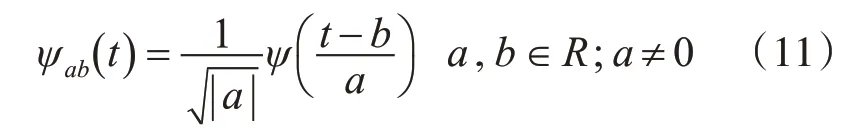
3）小波方差

小波方差即小波变换系数的平方值在b域上的积分［13］，其计算公式为

小波方差图是小波方差值伴随时间变化形成的曲线，该图可以解释在不同时间尺度上小波能量的分布状况。

4.6 距平

距平是显示气候要素偏离正常值的最常见的量。数据集中的某个数xi与平均数之间的差值就是距平，即：

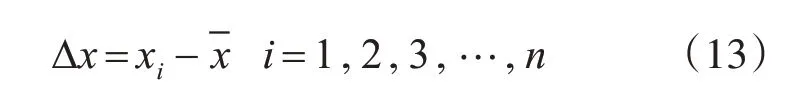
其中，一组气候变量数据x1,x2,xn与其平均数的差组成距平序列。

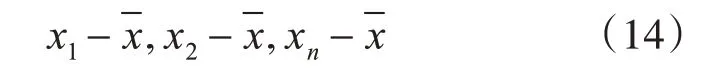
在气象研究中，经常选取距平序列来替换气候指标本身的观测值。

5 结果分析

5.1 年代际温度变化趋势

将数据按照时间序列输出距平值，反映了10年一个单位时间尺度上及整体的温度变化特征［12］，从图3 能够发现，加拿大各地区从1940 年起，70 年来每10 年单位时间尺度之间差异性较大，整体上温度有上升趋势。

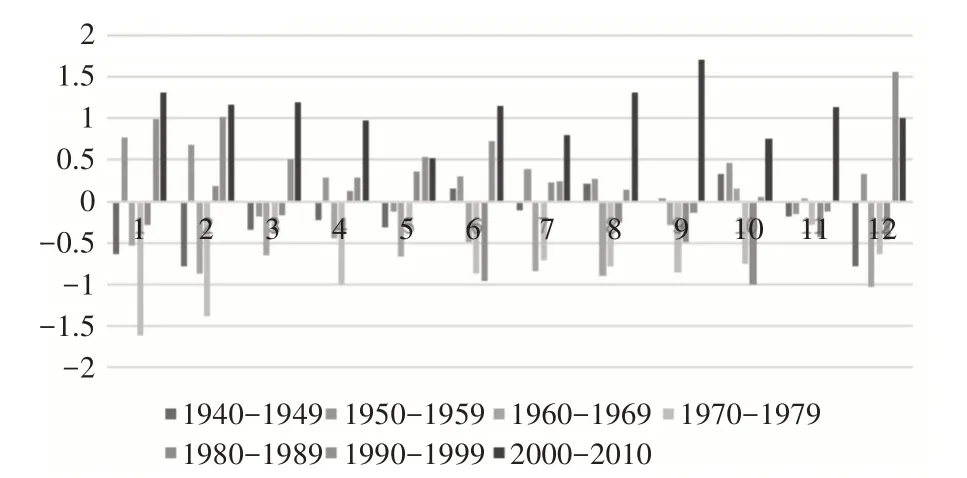
图3 温度变化趋势

通过统计各月的变化幅度，即图4可知，1月份每单位时间尺度实际地表温度与1940 年～2010 年地表温度均值相差度数分别是-0.64℃、0.76℃、-0.54℃、-1.66℃、-0.29℃、0.99℃以 及1.31℃，表明20 世纪40 年代至80 年代地表温度偏低，90 年代以及21 世纪00 年代地表温度偏高，总体表现为“升高-降低-升高”的变化趋势，与2、4、9月份各年代际地表温度变化趋势相似，都是70 年代气温偏低最严重。3 月的温度变化趋势“下降-上升”，类似于5 月份各年代际地表温度变化趋势，60 年代气温偏低最严重。6、10、11 月总体表现为“上升-下降-上升”的变化趋势，80 年代温度偏低最严重。7、8、12 月总体表现为“上升-下降-上升”的变化趋势，60 年代温度偏低最严重。除了12 月之外，温度升高最大的都是00年代，12月温度升高最大的是90年代。

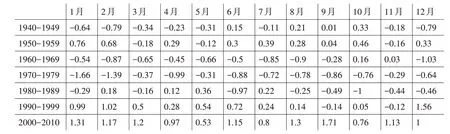
图4 各月实际地表气温和地表气温均值

经过观察分析，我们可以看出月份之间存在相似性，于是我们做了相关性分析，采用斯皮尔曼相关性分析做了进一步的相关性矩阵，具体如图5 所示。

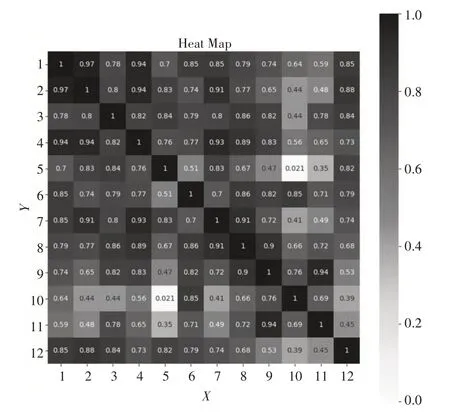
图5 相关矩阵

相关性系数分布在0～1区间，越靠近1，说明相关程度越高，越靠近0，相关程度越低，从图中可以看出，5 月和10 月相关关系最低，相关系数低至0.021。

5.2 基于ARIMA 分析温度序列变化趋势

通过ARIMA 模型对1940 年～2010 年的数据进行STL 分解，得出1940 年～2010 年随时间的温度变化趋势，如图6所示。

图6 1940年～2010年随时间的温度变化趋势

根据分解结果Trend 图的结论，温度仍然是出现先略微下降再升高的趋势。

5.3 温度的空间分布变化

1）反距离权重插值法

反距离权重插值法是常用的、易于理解的、方便实用的、比较好的空间插值方式之一，是一种精准插值，源于相近相似原理，具体表现为距离小，属性越接近，类似程度越高，相反，间距远，特性差别较大［14］。基于插值点与样本点之间的距离赋予权重求平均。间隔越小给予该点的权重值就会越大。经过查阅文献资料，我们选取ArcGIS 绘图软件，用反距离权重插值法在地图上绘制温度的空间分布［15］。

2）温度空间分布分析

加拿大幅员辽阔，主要城市分布在5 个气候区：太平洋地区（西海岸区）、平原地区、中部地区（大湖-圣劳伦斯蒂地区）、大西洋地区和北方地区，各个城市气候有着不一样的特点［16］。

我们可以从图7 中分析温度空间变化趋势，在这段时间中，加拿大所有地区的平均气温都有着不同程度的上升。上升比较慢的是东西海岸，大约在2℃～3℃之间。结合相关地理知识易于理解，靠近海洋的气候本来就是比较温和。

图7 温度空间变化趋势

内陆地区与沿海地区差别较大，大部分平均温度上升幅度都大于了4℃，北极三省的上涨幅度最大，基本都大于了6℃。显而易见，特别突出明显的是北极圈内，涨幅甚至超过了10℃。通过新闻可知，温室气体增加，由此导致温度上涨，成为了主要原因。

5.4 基于小波分析的海表温度规律研究

首先根据收集的数据对海表温度进行初步展示，并且对1981 年～2010 年一共30 年的数据进行小波分析，全球海表温度变化趋势、距平值及平均温度分布如图8、图9、图10所示。

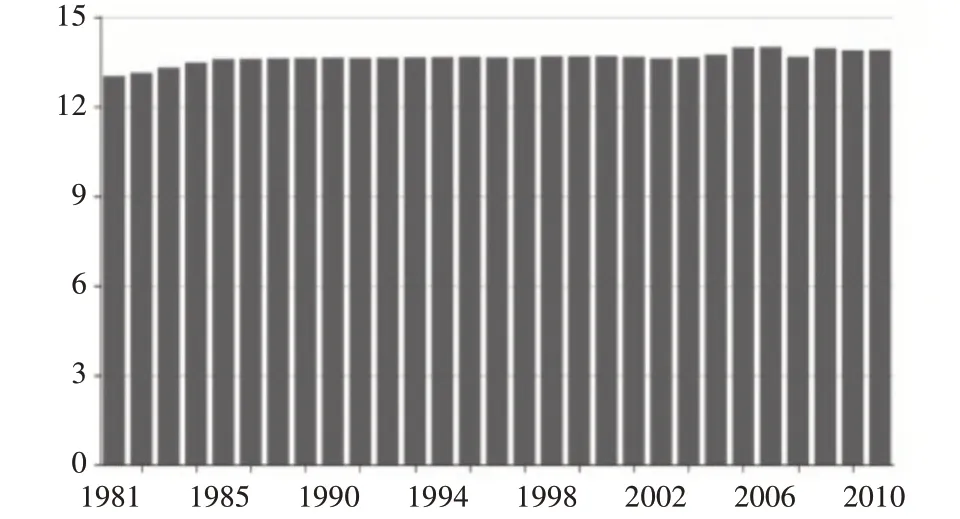
图8 全球海表温度变化趋势

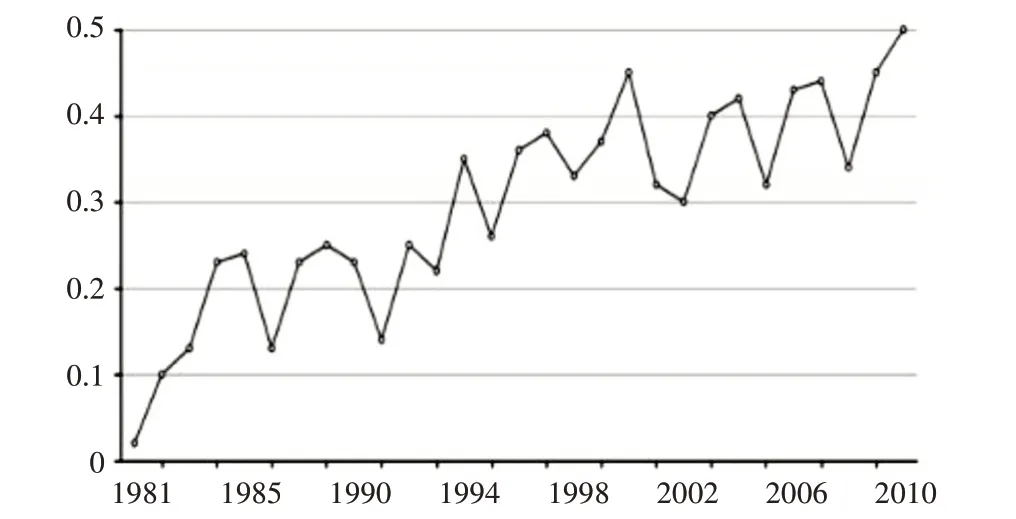
图9 全球海表温度距平值曲线图

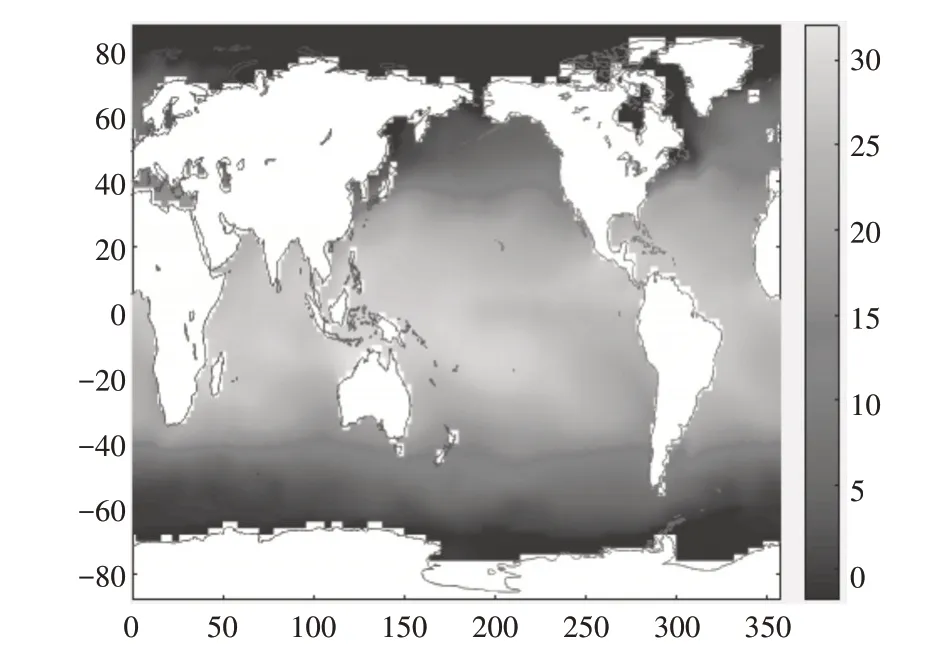
图10 全球海表平均温度分布图

全球海表温度在近30 年间总体呈现上升的趋势，如图8 所示，1981 年海表温度13.80 左右，在2006年出现最高温度，温度大约是13.99，增幅约为0.19。1981 年之后全球海表的距平值开始上升，1994 年到达第一个高峰，距平值约为0.35，在2010年出现最大距平。从图8 中可以看出，海表温度出现缓慢增长趋势，图9 呈现海表温度的距平在波动曲折中上升，图10 直观显示全球海表平均温度分布［17］。

生成函数选择墨西哥小帽小波，用一维相关连续小波对30 年这个时间段的数据集做变换操作，得到的灰度图直观显示小波变换系数绝对值的大小程度［12］。横轴为时间变换，纵轴为温度变化，图中越高的值，表征此处有越大的小波变换系数绝对值，意味着该时间段下海表温度变化越明显；小波变换系数为0 的坐标点是该尺度下海表气温变化的拐点［18］。为了准确地剖析30 年间海表温度的变化和突变特点，绘制了绝对值灰度图所对应的等值线图。通过等值线图11 可以得出，全球海表温度的变化周期约为10 年一个周期，在约5 年～6 年的尺度上有一个较强的扰动。

图11 等值线图

6 结语

6.1 模型评价

首先借助距平值揭示地表温度随时间变化的动态规律，得到12 个月的地表温度变化。通过ARIMA对1940年～2010年的数据进行STL分解，得到整体的气温趋势是略下降再上升的趋势［19］。对空间的温度趋势分析时，采用了反距离权重插值法和基于小波分析的方式对海表温度规律探究，能清楚的用数据和图表展示出1980 年～2010 年全球海洋表面温度的变化趋势可以得出全球海表温度的变化趋势为变暖的趋势。

由于收集到的数据中指标很多，初始样本量更是高达十万条，给数据量化处理工作带来很大困难，因此在筛选过程中会遗漏部分可能存在重要作用的变量信息，并且我们在求解权重的时候，可能方法不尽合理，会对结果产生一定程度的影响。最后，由于指标提取后，丢弃一些指标会造成小信息的丢失，所以得到的结论可能会存在一些可接受的误差。

收集的数据库中数据缺失很多，而这些缺失的数据对加拿大的气象站点的数据分析也是有影响的，虽然我们在进行建模和数据分析的时候，采用了K 最近距离邻法，对数据进行了填充，但是对最后的结果可能造成一定的误差。

6.2 模型改进

在分析空间和时间的温度变化趋势时，影响地表温度变化的因素中没有包括地形因素。由于气候的形成往往受到地形的影响，地表温度的空间分布因此发生了变化［20］。因此，若获取到更详细的地形数据集加入到考虑因素中分析时空分布的变化趋势，结果的准确度会显著提高。