氧化铝纳米流体液滴瞬态蒸发速率的演化特性分析

2022-08-01李钰璨胡定华刘锦辉

化工进展 2022年7期

李钰璨，胡定华，刘锦辉

（南京理工大学电子设备热控制工信部重点实验室，江苏南京 210094）

液滴蒸发是日常生产、生活中常见的物理现象。微小液滴蒸发时微观尺度的热力学驱动会引发宏观尺度的力学效应，具有较好的传热传质性能。纳米流体是由纳米尺度的颗粒加入基液并进行振荡等操作后得到的性状稳定的固液悬浮液。相较于其他传统溶液，纳米流体不仅保持了自身基液的相关性质，且纳米颗粒的加入还会在一定程度上改变流体黏度、流变性、稳定性等特性，因此有关微小纳米流体液滴蒸发特性的研究备受关注。纳米流体液滴蒸发时，纳米颗粒会受到多个力的协同作用，如范德华力、静电力、界面毛细力等，在液滴蒸发完全后，在这些不同力的作用下，纳米颗粒会在基板上形成不同的沉积图案，因此对纳米流体的蒸发沉积特性的研究在微尺度芯片制造、喷墨打印、农药喷洒和病理检验等领域都有广阔的应用前景。

纳米流体液滴的蒸发速率对蒸发过程中内部颗粒的运动产生影响，而颗粒运动同样也通过影响内部流场从而影响蒸发速率，因此研究纳米流体液滴的瞬态蒸发速率规律对进一步研究纳米流体的相关特性有重要意义。对液滴蒸发过程的数值研究目前有很多方法，陈剑楠等、Tanguy 等和谢驰宇等分别采用了体积函数法、水平集法和玻尔兹曼法来描述液滴形态，数值模拟液滴的蒸发过程。Hu等假设液滴在蒸发过程中是固定润湿线且保持球帽状的，用有限单元法求解了外部蒸汽浓度和蒸发通量，得出了利用蒸发速率作为接触角函数的经验表达式，并且探究了在忽略表面张力梯度和Marangoni 流的影响下蒸发液滴中的速度场。杨开采用任意拉格朗日-欧拉法（ALE），建立了全耦合的液滴瞬态蒸发模型。Cazabat 等在假设液滴内部温度相同的条件下计算得出了蒸发速率的公式，并且探究了液滴半径、界面蒸汽浓度等因素对蒸发速率的影响。事实上，由于考虑到蒸发冷却效应和基板与液滴的热传递，等温假设在现实中很难实现，Semenov 等将热量传递加入蒸发模型，完善了先前的蒸发速率公式。实验研究方面，Gerken等通过实验发现，相对于纯水液滴在超疏水表面上的蒸发，纳米颗粒的加入使得蒸发过程明显缩短，纳米流体液滴的体积与时间关系曲线的斜率随时间有所减小。Sefiane等进行了加热聚四氟乙烯（PTFE）底板上的铝-乙醇纳米流体液滴蒸发实验，发现加入纳米颗粒使基液的热导率提高、黏度增大，从而使得液滴在定接触半径蒸发时的蒸发速率下降。Trybala等在聚乙烯（PE）、PTFE和硅片三种不同润湿性的基体上，对无机纳米颗粒TiO、SiO、碳的水基纳米流体的固相液滴蒸发动力学进行了实验研究，发现纳米流体在较高热导率的固体载体上蒸发速率更高，且蒸发速率与纳米流体本身的热导率有一定关系。此外，气相环境中的自然对流也对纳米流体液滴的蒸发有促进作用，Sobac等实验证明了气相环境中的浮升力会使得液滴的蒸发速率有所增大。

目前关于纳米流体液滴蒸发过程的研究多集中在蒸发速率的影响因素上，有关液滴瞬态蒸发速率在蒸发过程进行中的演化特性方面的研究相对欠缺。本文基于ALE 法建立了纳米流体液滴蒸发的瞬态模型，耦合了液滴蒸发过程中蒸汽浓度场、纳米颗粒浓度场、气液固温度场以及液滴内部流场等多个物理场，同时考虑了液滴气液界面Marangoni流效应，模拟了粒径为50nm 的氧化铝纳米流体液滴在恒温水平玻璃基板表面的蒸发过程，研究了随着蒸发过程进行液滴的瞬态蒸发速率的变化规律，探究了液滴内部颗粒体积分数与基板温度的变化对蒸发过程中瞬态蒸发速率的影响，并开展了相应的液滴蒸发实验，对数值模型和结果进行了验证。

1 数值模型与实验系统

1.1 液滴蒸发过程的数值模型

1.1.1 物理模型

如图1所示，初始高度=1mm，接触半径=1mm 的氧化铝纳米流体液滴在一水平玻璃基板上表面蒸发。假设纳米流体液滴蒸发时始终可被视为球冠，纳米颗粒均匀地分散于基液中，且蒸发模式为恒接触半径蒸发（CCR），接触半径保持不变，接触角随蒸发过程进行逐渐减小。模型为二维对称结构，玻璃基板温度恒为，环境温度=20℃，设定相对湿度=45%。

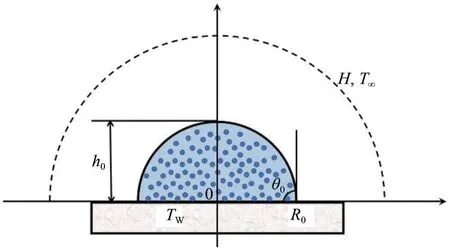
图1 纳米流体液滴蒸发模型示意图

纳米流体的密度计算公式见式(1)。

式中，为纳米颗粒体积分数。

比热容计算公式见式(2)。

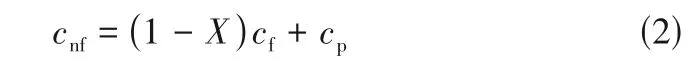
式中，和分别为水和纳米颗粒的比热容。动力黏度计算公式见式(3)。

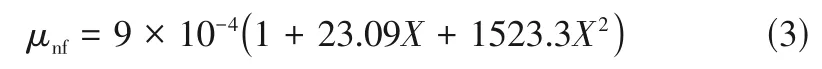
环境温度下纳米流体的表面张力计算公式见式(4)。

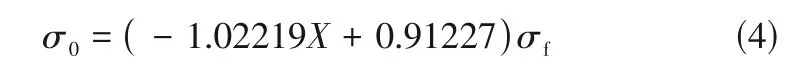
式中，为水在环境温度下的表面张力，20℃条件下水的表面张力=72.75mN/m。

已知蒸发过程中纳米流体的表面张力与温度有关，则有式(5)。

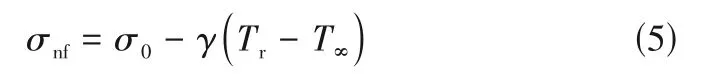
式中，为液滴表面处的温度；为表面张力-温度系数。

纳米流体的热导率可以表述为式(6)。

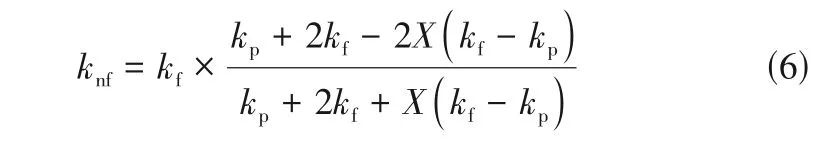
式中，和分别为水和纳米颗粒的热导率。

此外，本文所建立的液滴蒸发模型作了如下假设：液滴气液两相界面处的蒸汽处于饱和状态；液滴内部pH 一定，忽略颗粒与颗粒之间及颗粒与基板间的DLVO 作用力；不考虑温度对比热容、黏度和热导率的影响及纳米流体液滴不稳定性的影响；液滴中的纳米颗粒在蒸发过程中没有扩散至蒸汽环境，蒸发结束后均沉积在基板表面。

1.1.2 数学模型

（1）任意拉格朗日-欧拉（ALE）法

描述流体运动的主要方法分为拉格朗日法和欧拉法。拉格朗日法的网格点跟随流体质点运动，而欧拉法的网格点固定在空间中。任意拉格朗日-欧拉（ALE）法则能够结合上述两种方法的优点，使网格点既可以随流体质点变形，但又不必完全依附流体质点，从而能更有效地捕捉流体的交界、动态界面。本文采用ALE法实现对液滴气液两相界面在蒸发过程中运动的捕捉。

在ALE 坐标系中，定义对流速度的表达式为式(7)。

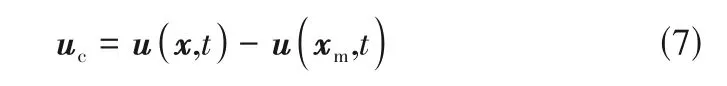
式中，和分别为物质坐标和网格坐标；(,)和(,)分别为物质点、网格点的空间速度。

由此可得物质时间导数见式(8)。

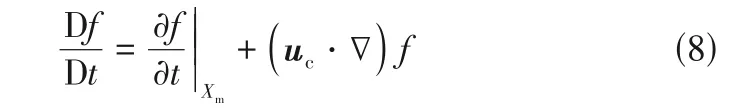
式中，∇为空间梯度算子。

（2）控制方程

蒸发过程中，流体区域内连续性方程、动量方程见式(9)、式(10)。

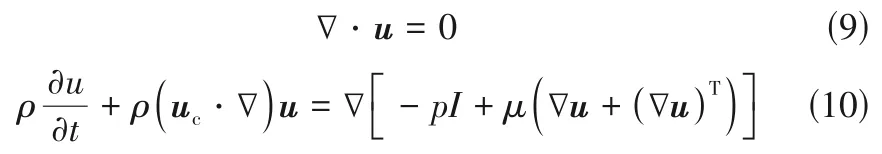
式中，为流体速度；为流体密度；为流体内部压力；为流体动力黏度。

蒸发过程中液滴与蒸汽环境之间能量守恒，则有式(11)。

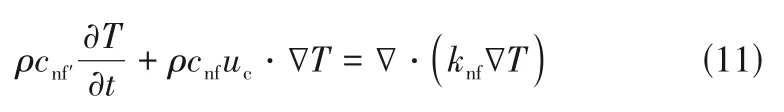
式中，为流体温度。

蒸汽的扩散方程见式(12)。

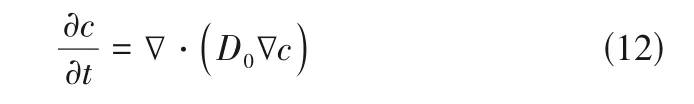
式中，为蒸汽浓度；为蒸汽扩散系数，本模型中参考取值=2.61×10m/s。

对于含颗粒的纳米流体液滴，内部颗粒对流扩散方程见式(13)。

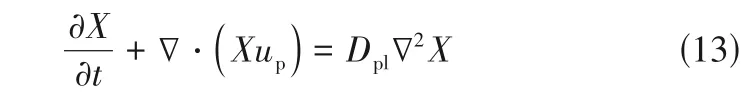
式中，为纳米颗粒的扩散系数。对于水中粒径50nm 的氧化铝纳米颗粒，其扩散系数约为1.7×10m/s。

液滴内部的Marangoni流作用可描述为式(14)。

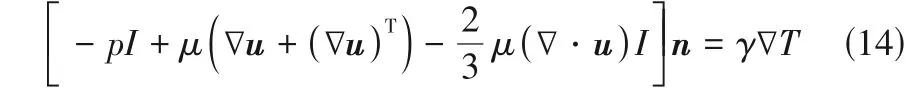
（3）初始及边界条件

初始条件：当=0时，液滴的内部各点温度均等于液滴外部环境温度，且液滴内部流体无运动。

边界条件：在=0处，温度始终保持基板温度，且无质量传递。

在=0 处，采用轴对称边界条件，径向无质量、热量传递。

在=100处，相对湿度保持不变，蒸汽浓度与有以下关系，见式(15)。

在气液两相界面处，蒸汽处于饱和状态，则有饱和大气压、饱和蒸汽浓度，见式(16)、式(17)。

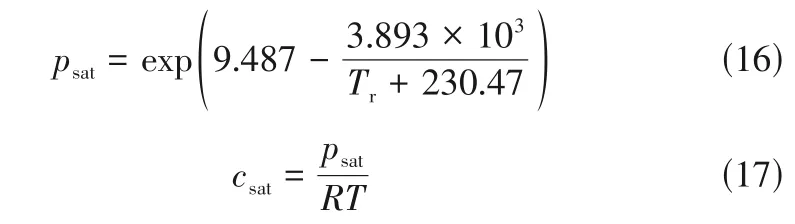
液滴在气液两相界面的局部蒸发流量见式(18)。

式中，为蒸汽的摩尔质量，kg/mol。

液滴的蒸发速率见式(19)。

式中，为液滴气液两相界面的表面积。

蒸发过程中气液两相界面处的液滴与外部环境的换热量见式(20)。

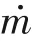
1.1.3 模型求解

本文使用COMSOL 软件求解上述模型。本模型中网格使用的是三角形划分，在气液两相界面、气液固三相接触线附近进行自适应网格细化处理，最大网格单元的尺寸为1×10mm。为保证计算的精确性，气液两相界面处网格质量小于0.1 时，两相界面处的网格将会自动再次进行划分。图2所示为初始时刻时模型计算域中液滴及液滴周围的网格划分结果。瞬态求解器采用向后差分法，初始时间步长设为1×10，最大时间步长设为1×10，并依据模型计算进程中的收敛情况自动调整步长。采用大规模稀疏矩阵求解器进行线性求解，非线性求解器采用牛顿阻尼法，阻尼因子设为1。

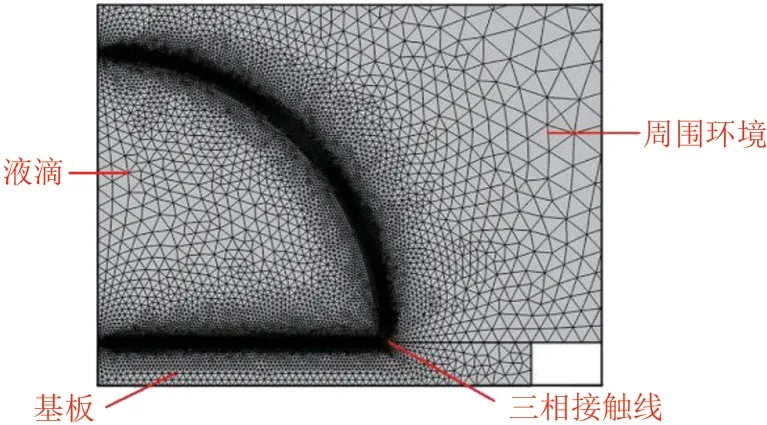
图2 纳米流体液滴网格划分结果

基于上述模型，在设置基板温度为40℃、纳米颗粒初始体积分数为2%的条件下，采用不同的网格数进行计算，验证网格无关性。表1所示为三种不同网格数条件下计算得出的液滴蒸发速率的最大相对偏差，网格数为27779 时最大相对偏差仅为1.03%，为提高计算效率、保证计算的准确性，本文使用该网格数进行计算。

表1 网格无关性验证

1.2 蒸发实验系统

1.2.1 实验方法

本实验中用到的分散液为氧化铝纳米流体溶液，纳米颗粒是平均粒径为50nm 的球形氧化铝纳米粒子，基液为去离子水，采用“两步法”进行纳米流体的制备。图3为实验装置图。控制室内温度为25℃±2℃，相对湿度为45%，对纳米流体液滴进行蒸发实验研究，具体实验步骤如下。

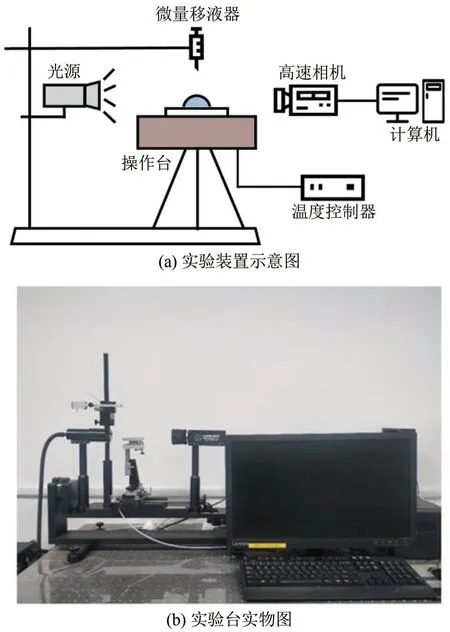
图3 实验装置图

（1）使用电子天平称量一定质量的去离子水和纳米颗粒，在烧杯内进行稀释混合。将烧杯置于磁力搅拌器上搅拌15min，再使用超声波振荡器进行振荡30min，得到纳米流体。

（2）设定恒温水浴槽的加热温度并开始预加热。当恒温水浴槽达设定温度时，用镊子将完全清洗后的玻璃载玻片放在实验装置台上，使用微量移液器取2μL 纳米流体液滴滴在载玻片上开始蒸发。

（3）液滴蒸发过程中，用高速相机记录接触角的大小并观察液滴接触线处颗粒的运动情况和液滴的轮廓变化。

1.2.2 瞬态蒸发速率的计算

通过分析高速相机实时拍摄的不同时刻的液滴照片，可测得液滴接触角和接触半径等参数。由于液滴在蒸发过程中保持球冠形，即可计算液滴体积，见式(21)。

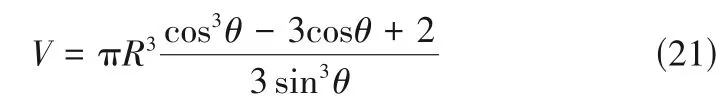
利用中心差分法处理计算得出的液滴体积的相关数据，得出液滴瞬态蒸发速率，见式(22)。

式中，V为第个测量数据点计算得出的液滴体积；Δ为数据点的间隔时间。

2 结果与讨论

2.1 瞬态蒸发速率的模型验证

图4给出了模拟计算与蒸发实验分别得到的在基板温度45℃条件下纯水液滴蒸发过程中蒸发速率随时间的变化曲线。图4中模拟结果与实验结果均显示，随着蒸发过程的进行，纯水液滴的瞬态蒸发速率呈现逐渐减小的趋势。另外，从瞬态蒸发速率数值大小的角度分析，模拟与实验的结果相对误差小于13.1%，可以认为本文模型具有合理性，能够较为准确地进行液滴蒸发动态过程的计算分析。

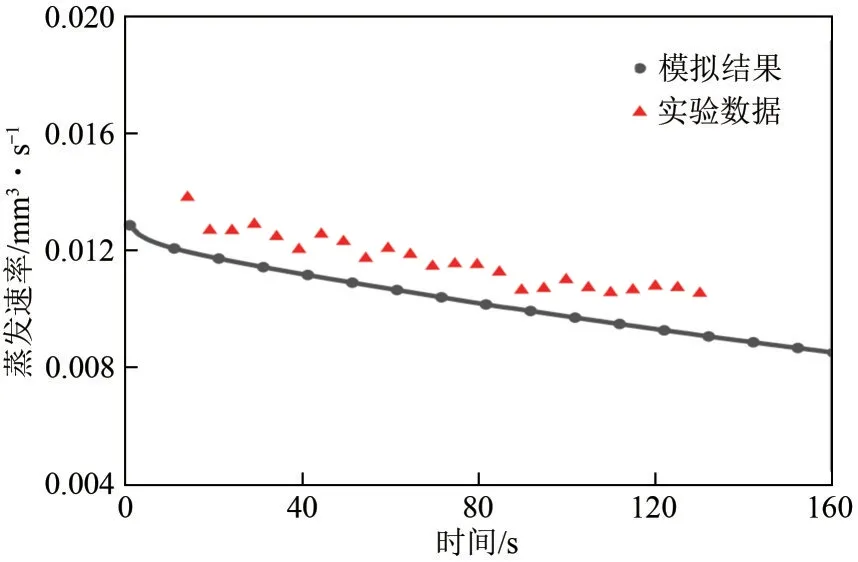
图4 纯水液滴瞬态蒸发速率随时间的变化关系

2.2 液滴瞬态蒸发速率随时间的变化特性

液滴的蒸发速率受到多种因素的影响，如环境温湿度、基板表面情况以及液滴自身物性等。其中，在纯水中加入纳米颗粒，可以改变流体的热力学特性，并且影响液滴蒸发过程中内部流场的分布情况。本文主要通过数值模拟的方法，研究纳米流体液滴在蒸发过程中其瞬态蒸发速率与蒸发时间的关系。

图5 给出了模拟计算得到的相同基板温度（45℃）条件下，纯水液滴和不同初始颗粒体积分数（2%、1%、0.1%）的氧化铝纳米流体液滴蒸发过程中蒸发速率随时间的变化曲线。从图5中可以看出，在蒸发过程的前期阶段，两种液滴的蒸发速率均随蒸发时间的增加而减小。在蒸发过程进行到后期时，纳米流体液滴的蒸发速率突然增大，而纯水液滴则仍然保持减小的趋势。对比两种液滴，可以发现纳米流体液滴的瞬态蒸发速率整体大于纯水液滴，蒸发时间也明显缩短。由此可见，纳米颗粒的加入可以强化液滴的蒸发。

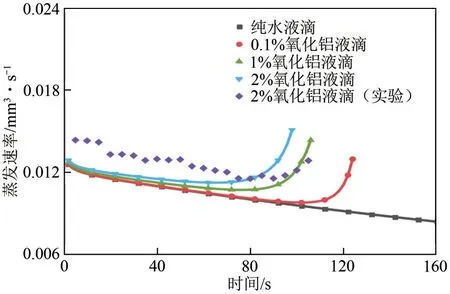
图5 纳米流体液滴和纯水液滴的瞬态蒸发速率随时间变化关系

在纳米流体液滴蒸发前期，瞬态蒸发速率随时间呈逐渐减小的趋势。这是由于在液滴蒸发过程中，瞬态蒸发速率与液滴的气液界面的面积有直接关系。纳米流体液滴在蒸发前期处于定接触半径蒸发模式，即在蒸发过程中接触线钉扎、接触角逐渐减小、液滴高度逐渐降低。所以在这种模式下气液界面表面积不断减小，从而使得瞬态蒸发速率逐渐降低。对于纯水液滴而言，瞬态蒸发速率逐渐降低的变化趋势贯穿蒸发过程的始终，曲线斜率也保持恒定。然而纳米流体液滴由于内部颗粒浓度不断增大，一定程度上强化了液滴内部的传热，使瞬态蒸发速率能够维持在较高的水平，故曲线斜率逐渐减小。

图6给出了瞬态蒸发速率与液滴内部颗粒体积分数变化之间的关系。研究发现，不同初始颗粒体积分数的纳米流体液滴的瞬态蒸发速率曲线驻点均在颗粒体积分数约26%处。这说明随着蒸发过程的进行，液滴内部颗粒体积分数达到26%时，颗粒在液滴内部的运动对液滴表面的蒸发行为的影响增大，并且超越了液滴表面积变化对蒸发的影响，使得瞬态蒸发速率的变化趋势发生改变。

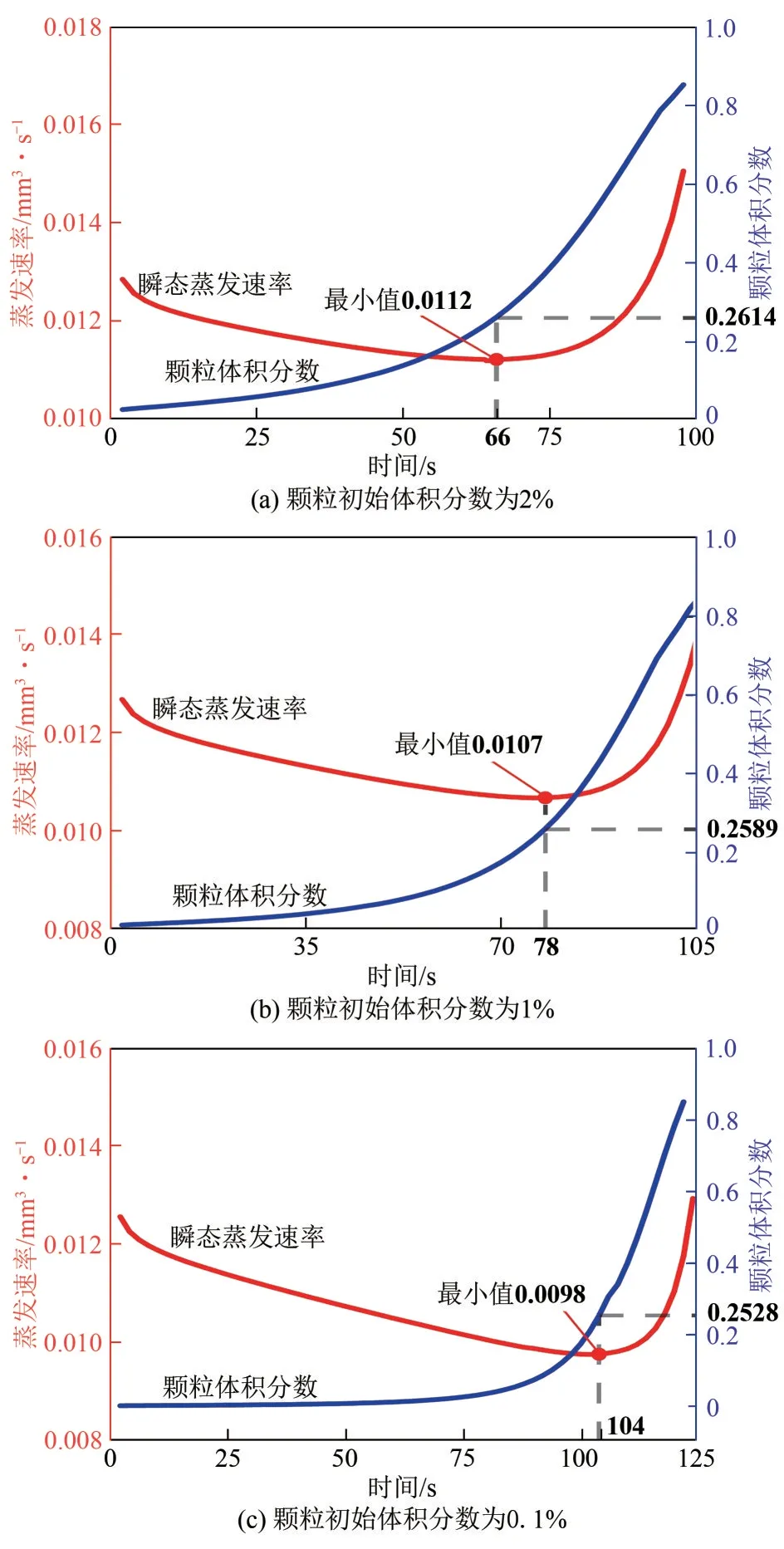
图6 瞬态蒸发速率与纳米颗粒体积分数的关系

纳米流体液滴蒸发后期，瞬态蒸发速率会呈现迅速增大的趋势。这是由于趋于蒸发完全时液滴内部基液含量较少，蒸发使得颗粒在液滴中的占比快速增大，流体热导率较大，局部蒸发流量较高，瞬态蒸发速率显著提升。同时，如图7所示，在蒸发过程中液滴内部颗粒分布会随时间发生一定变化。蒸发后期大部分纳米颗粒已经附着在基板上，且大多颗粒在三相接触线附近聚积，使得液滴高度下降到一定程度后会形成一层附着在边缘堆叠颗粒上的液膜，增大了气液界面面积，从而增大了瞬态蒸发速率。

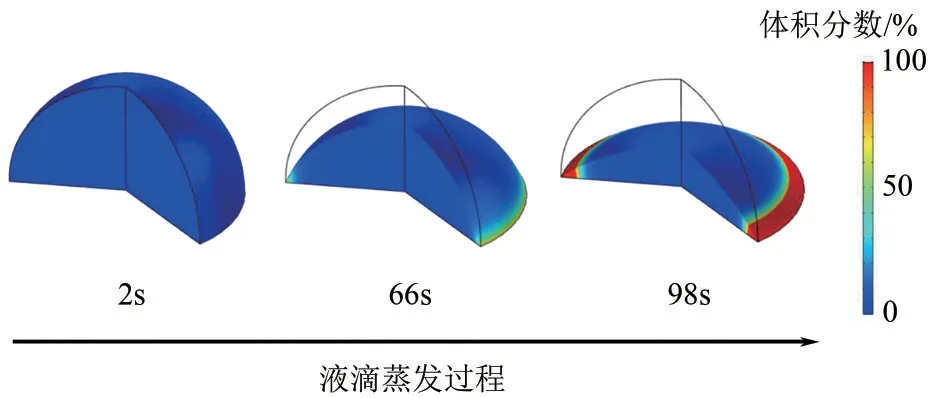
图7 蒸发过程中液滴内部颗粒浓度分布的变化

另外，因受到Marangoni 流的影响，蒸发过程中颗粒浓度的增大也加强了液滴的对流换热，使得液滴蒸发加快。图8为纳米流体液滴蒸发过程中温度场和流场的动态变化示意图。如图8所示，液滴内部的Marangoni 流随时间的增加而逐渐增强，液滴中传热较强的位置也由液滴的三相接触线向液滴的内部缓缓移动，液滴内部温差逐渐减小，可见Marangoni 流可以强化液滴内部的传热过程，从而促使纳米流体液滴瞬态蒸发速率的增大。在蒸发后期，Marangoni 流引发了较为明显的流场变化，液滴边缘处的反向回流较强，也是造成瞬态蒸发速率快速加大的重要原因。

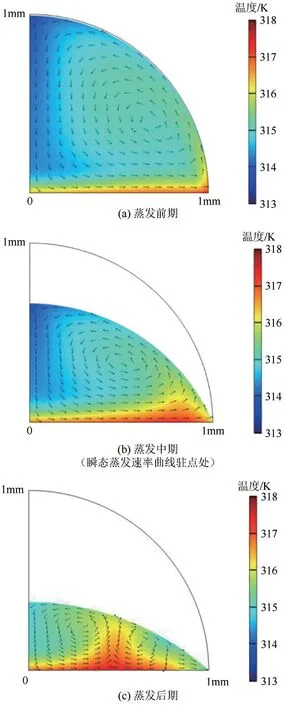
图8 液滴内部温度场及流场分布

2.3 基板温度对液滴瞬态蒸发速率的影响

温度是影响流体蒸发速率的重要因素，本文主要研究基板温度对液滴蒸发过程的影响。图9分别给出了不同基板温度（30℃、40℃、50℃）条件下，纯水液滴与颗粒初始体积分数为1%的纳米流体液滴的瞬态蒸发速率随时间变化情况。对于同一种液滴，基板温度的升高导致液滴的瞬态蒸发速率加快、蒸发时间缩短，但基板温度的变化无法改变同种液滴的瞬态蒸发速率变化趋势。对比三个温度下的蒸发模型的计算结果，发现基板温度每升高10℃，液滴在蒸发前期的蒸发速率增大约4.4%，蒸发全过程平均蒸发速率增大约4.8%，总蒸发时间缩短约6.23%。

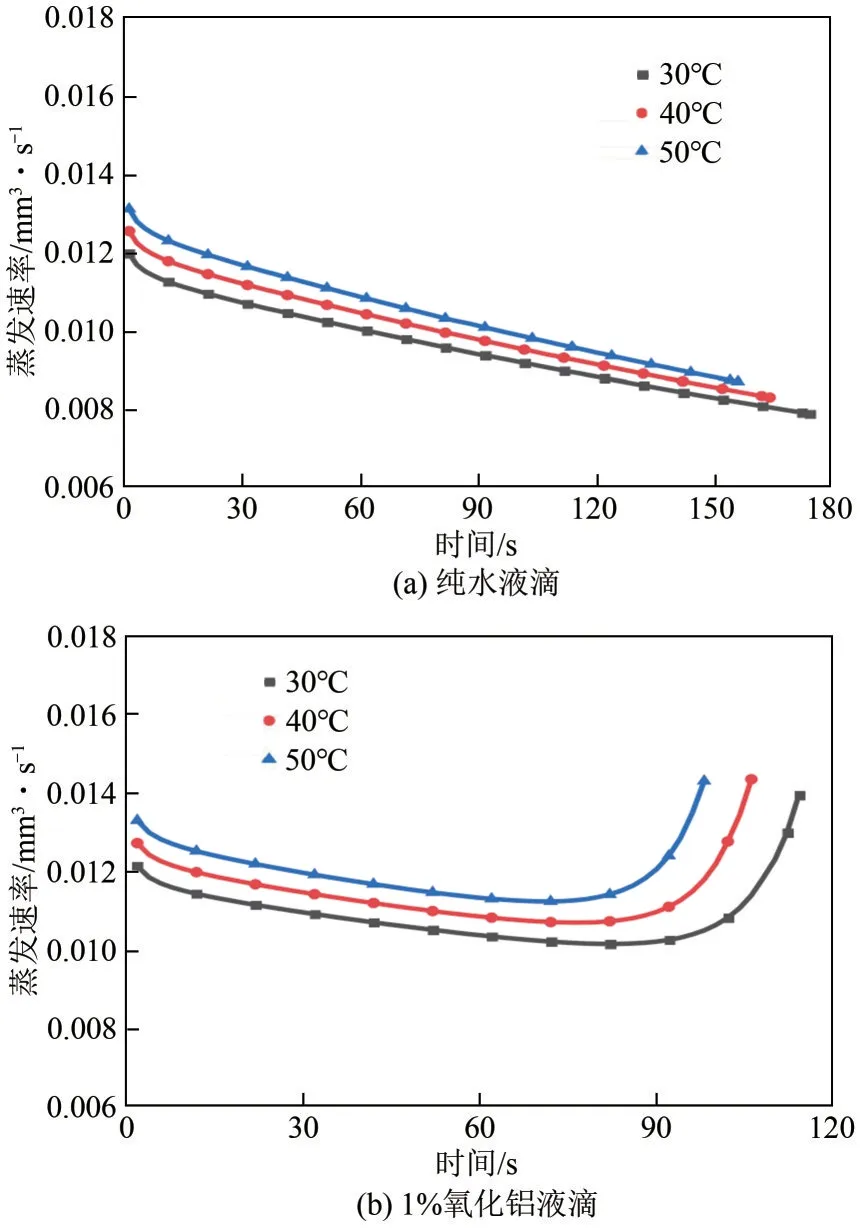
图9 不同基板温度条件下液滴的瞬态蒸发速率随时间变化关系

基板温度的升高使得液滴对流换热增强，加速了内部流体流动，增大了颗粒间的扰动，从而增强气液界面的流体蒸发。图10 给出了基板温度与液滴内部颗粒体积分数之间的关系，可以看出，基板温度越高，颗粒体积分数增大越快，使得瞬态蒸发速率曲线的驻点前移，整体上加速了液滴的蒸发。另外，由于液滴气液界面的蒸汽浓度仅与温度有关，所以基板温度的升高会导致气液界面的温度升高，使得液滴附近蒸汽浓度提高，与环境的蒸汽浓度梯度增大，加快液滴的蒸发。